基于MFD的模擬超飽和路網交通控制策略優化

朱麗葉，張 勇

(蘇州大學城市軌道交通學院，江蘇 蘇州，215131)

隨著交通出行的快速機動化，城市道路交通擁堵日趨嚴重。然而，當城市道路可改造空間有限時，采用交通信號控制來緩解城市常發性超飽和交通堵塞幾乎是唯一的選擇。傳統的區域交通控制策略主要是圍繞減少車輛通過交叉路口的飽和度、排隊長度或者延誤時長而展開, 以控制路段上車輛數最小化來保證控制策略的最優,該控制策略在緩解交通擁堵方面取得了一定的效果，但是還缺乏對路網整體通行效率的優化控制。交通流宏觀基本圖(Macroscopic Fundamental Diagram,簡稱MFD)的控制思路從理論上證明了在路網上的車輛數量與離開路網的交通流量呈現單峰的關系[1-2]，這一發現對超飽和交通控制具有重要的意義。在實際路網控制中，為了避免超飽和交通的影響，相關控制方法會將未飽和與過飽和兩種控制狀態結合考慮，進行不同狀態下控制方案的變換,或者以某種穩態作為參照進行反饋調節控制，從而避免路網出現擁堵，例如，Dinopoulou等[3]基于輸入-輸出模式建立路段車輛數的狀態方程，并以路段累積車輛數為0時的穩態控制方案作為參照，提出了可自動響應當前交通需求并進行反饋調節的TUC控制策略。

目前，MFD主要用于邊界控制，研究方法可以分為兩大類,其中第一類是解析研究區域的MFD形態后再進行堵塞區域的優化控制，比較典型的控制方法為Bang-Bang控制[4]，但是在實際控制過程中，由于控制方法對控制邊界的強烈依賴，對于多區域的共用邊界控制將成為其控制難點；第二類研究方法是考慮到實際控制區域路網MFD的不確定性，對控制系統進行魯棒調節，但其控制器設計難度較大。盡管MFD可以直接描述路網系統的累積車輛數和輸出效率之間的關系，但對系統的同質性要求很高，在實際路網中，由于路網基礎結構(包括公交專用道、單行線等)不同，會使區域的MFD形態產生不同程度的發散，因此難以找到普適性的MFD及控制方法，有必要開展基于MFD的超飽和路網交通控制策略優化研究。為此，本文以堵塞區域路網各條路段上行駛的車輛數作為狀態變量，建立路網交通的狀態方程，分析路段上車輛數變化規律；同時，基于交通流MFD，以路網中路段累積車輛數作為控制目標，建立關于堵塞區域路網系統的離散狀態優化控制模型，并將該模型在某城市新區進行模擬算例應用，以期為基于MFD的城市交通路網區域實時信號控制提供參考。

1 模型構建

1.1 控制策略

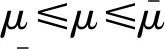
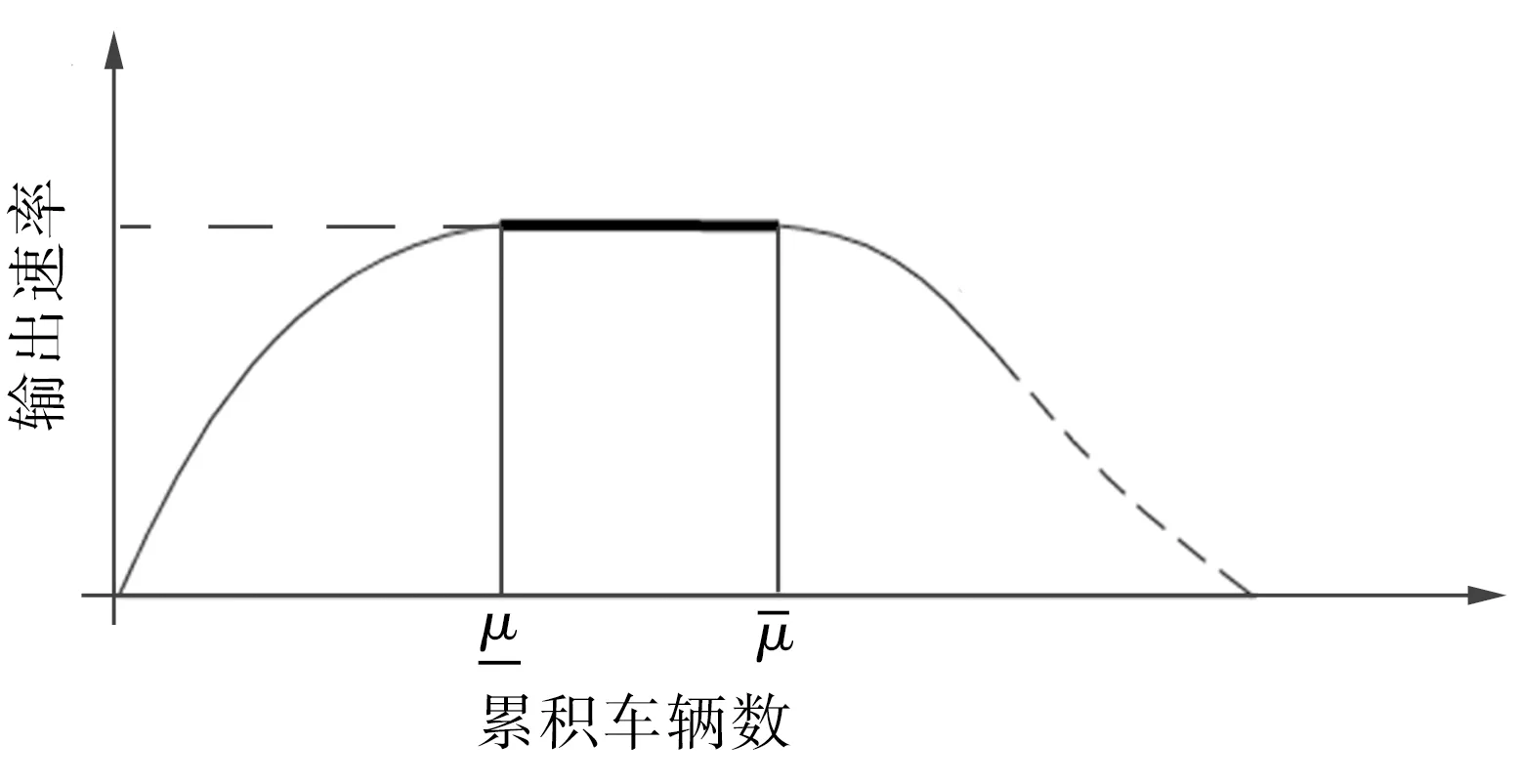
圖1 路網中車輛數累積量與通行率關系圖

本文從路段層面借鑒MFD的控制思想，在保證路段車流不出現擁堵的前提下，使路網區域的車輛分散到各路段上，形成路段的最優車輛數累積量。根據車流的流量-密度關系模型，當車流在非擁堵狀態達到最大密度時，其輸出流量也最大，這與路網系統MFD屬性所描述的關于路網累積量和路網輸出率之間的關系不謀而合。很顯然，如果所有路段的車流狀態都能達到流量-密度模型的最高點，路網的信號控制將不必存在。在關于路網MFD屬性的研究中發現，路網系統的最優車輛數累積量與其本身結構和基礎設置有關，其最優車輛數累積量是一個定值，且遠小于所有路段達到最優車輛數累積量的總和。因此，這種基于路段車輛數累積量的設置方法可以保證路網系統達到最優車輛數累積量，同時路網中各路段也不會出現堵塞現象。

1.2 交通流建模

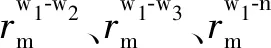
根據車輛守恒原理，可以寫出某路段上(k+1)T時刻的車輛數，其路段的車輛數等于kT時刻的車輛數加上在T時間流入的車輛數和流出的車輛數差值，即：

xZ(k+1)=xZ(k)+T[ΔuZ(k)+ΔdZ(k)]/3600

(1)

ΔuZ(k)=uZ(k)-u′Z(k)

(2)

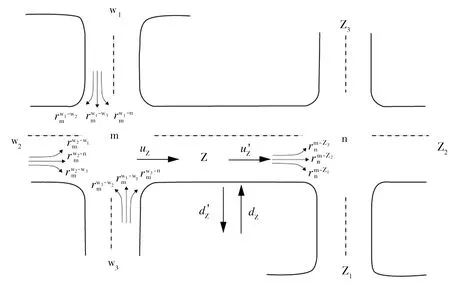
圖2 路段及關聯兩交叉口交通流分布(單向)

Fig.2 Traffic flow distribution of road segment and section linked of two intersections (one-way)

ΔdZ(k)=dZ(k)-d′Z(k)

(3)

式中:k表示控制狀態指標；T表示控制時間步長，s；xZ(k)表示路段Z在kT時刻的車輛數；uZ(k)、u′Z(k)分別為路段Z在kT時刻的輸入端和輸出端的實際流量值，veh/h；dZ(k)、d′Z(k)分別為在kT時刻路段Z中間位置的實際流入和流出流量值，veh/h；ΔuZ(k)表示路段Z在kT時刻產生外生流量差值，veh/h；ΔdZ(k)表示路段Z在kT時刻產生內生流量差值，veh/h。

車流在路網中運行時涉及到路網中路段和交叉口的相關拓撲關系，為了簡化模型，將對車流通過交叉口時的有關相位變換過程、車流運行過程進行如下假設：第一，在控制的初始時刻路網中有一定的車輛數累積；第二， 任意交叉口j的周期時長固定且已知，其值為C0j，每周期的總損失時間固定且已知，其值為Lj,那么，交叉口j在每個周期的總綠燈時長固定且已知，即Cj=C0j-Lj；第三， 任意路段Z的輸出車流通過交叉口的飽和流率為S；第四，各交叉口的相位均為固定的四相位組合模式，沒有優先相位或其他特殊相位。

當路段上、下游交叉口的控制周期固定，相關相位已知，根據輸出車流的轉向比(r)和綠燈時間(g)的對應關系，并用路段連接的上、下游交叉口代替原路段的名稱，可以將公式(1)寫成帶有一定結構的矩陣相乘的形式，即基于輸入-輸出模式的狀態方程為：

xmn(k+1)=xmn(k)+

(4)

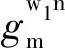
如果將路段的上、下游節點拓展到路網范圍，可以進一步寫出符合路網拓撲關系的離散狀態方程為：

X(k+1)=X(k)+B(k)G(k)+TΔD(k)

(5)

式中：X(k)表示路段車輛數狀態變量矩陣，矩陣大小和結構與路網結構和所包含路段的數量有關；B(k)為流量矩陣，各元素表示特定路段上輸出車道組的流量大小，矩陣大小以及拓撲關系與路網結構有關；G(k)為控制變量矩陣，矩陣元素表示路段輸出車流通過交叉口時綠燈相位時長，矩陣結構與B(k)對應；ΔD(k)為內生流量矩陣，矩陣形式和X(k)相同。

1.3 控制模型與求解

當確定各路段車輛的最優累積量參照值后，根據累積量最優的控制思想，則可以采用一個二次多項式形式表示最小化控制目標為：

(6)

式中：μmn表示交叉口m、n連接路段上最優車輛數累積量參照值，veh。將控制目標添加相應的權重系數矩陣Q，可以寫出該模型的控制函數：

(7)

式中:NK表示總的控制步數；狀態變量矩陣X(k)滿足公式(5)；路段車輛累積量參照值矩陣μ需根據路網系統交通狀況進行調整，以保證路網系統穩態為基礎，盡可能提高路網的輸出效率；在進行優化控制的過程中，權重系數矩陣Q和路段車輛累積量參照值矩陣μ將直接影響優化控制的結果。根據MFD的路段累積量最優的控制思想，優化控制模型中各路段車輛數均需保持在最優累積量的附近波動，由此，權重系數矩陣Q可以取單位矩陣。

AG(k)-C=0

(8)

式中:A為G(k)矩陣的系數矩陣，其矩陣形式與交叉口各相位以及G(k)矩陣的結構有關；C矩陣表示各交叉口的總綠燈時間，由交叉口的周期時長和總損失時間決定，當周期時長和總損失時間已知，則C為常數矩陣。當交叉口設置各相位綠燈時長時，需要考慮最小綠燈時間約束，即：gj,i≥gj,i,min,i∈Fj，則控制變量矩陣G(k)的線性不等式約束用矩陣的形式可以表示為：

Gmin-G(k)≤0

(9)

式中:Gmin為gj,i,min的矩陣形式，矩陣結構與G(k)相同，其中，gj,i,min表示交叉口j的綠燈相位最小時長，當交叉口各綠燈相位的最小綠燈時長已知，則Gmin為常數矩陣。

由公式(5)、(7)、(8)、(9)構成了有約束的離散狀態優化控制模型，且狀態變量矩陣X(k)的初始狀態已知。由于該模型是凸函數，因此模型的局部最優解就是全局最優解。根據龐特里亞金極小值原理，可通過構造模型的哈密爾頓函數來求模型的極小值，引入拉格朗日乘子λ(k+1)T和KKT因子η(k)T、σ(k)T，構造模型的哈密爾頓函數H(k)，則有：

λ(k+1)T[X(k)+B(k)G(k)+TΔD(k)]

+η(k)T[AG(k)-C]+σ(k)T[Gmin-G(k)]

(10)

再根據哈密爾頓函數和約束條件，建立極值條件，尋找哈密爾頓函數的K-T點，則有：

B(k)G(k)+TΔD(k),X(1)=X0

(11)

(12)

(13)

σ(k)T[Gmin-G(k)]=0,σ(k)≥0

(14)

優化模型通過求解每個狀態的K-T點來得到控制變量矩陣G(k)在每個狀態的最優解。本文將采用梯度投影法，通過計算控制變量矩陣G(k)當前可行解的有效約束矩陣和其關于哈密爾頓函數H(k)的偏導(見公式(13))所構成的投影矩陣來確定當前的迭代方向，并根據當前可行解和迭代方向運用黃金分割法尋找當前最優迭代步長，以此確定新的可行解，直到新的可行解滿足KKT條件(見公式(14))，此時所得的可行解即為模型的K-T點。具體求解步驟可參考文獻[5]。

2 實例分析

本次實驗區域的路口均為十字形路口，采用傳統的四相位、定周期控制。定時配時方法為：根據規劃高峰小時數據，用Webster模型計算各交叉口高峰小時車道組飽和度，并確定配時方案，各交叉口周期固定為C=120 s。采用本文上述控制模型，并根據路網外圍輸入流量矩陣B(k)實時優化控制方案。

2.1 試驗區域概況

以襄陽市東津新區為試驗區域，根據MFD區域的劃分方法，路網范圍為5～10 km2，試驗控制區域路網如圖3所示。從圖3中可以看出，該區域中共有6條相交道路、9個內部控制交叉口、12個外圍連接交叉口，區域總面積約為6 km2。交叉口連接的路段長度均在400～1100 m范圍內，路段的單向車道數為2～3條。在本研究中，不考慮控制路網外圍連接的下游輸出路段對路網系統的影響，均用單一的有向線段表示路網外圍連接的輸出路段。為了模擬高峰小時的超飽和路網流量，將擬定路網外圍連接路段的單車道平均流量，在模擬時間內，外圍路段的平均輸入流量會隨著時間波動，路網輸入流量隨時間變化的曲線如圖4所示。圖4中采用間隔4 min的流量輸入變化來模擬高峰小時路段流量流入的波動情況，路網外圍的輸入流量每4 min變化一次。在此模擬過程中，車流經過交叉口的轉向比例與規劃高峰小時流量的轉向比例相同。

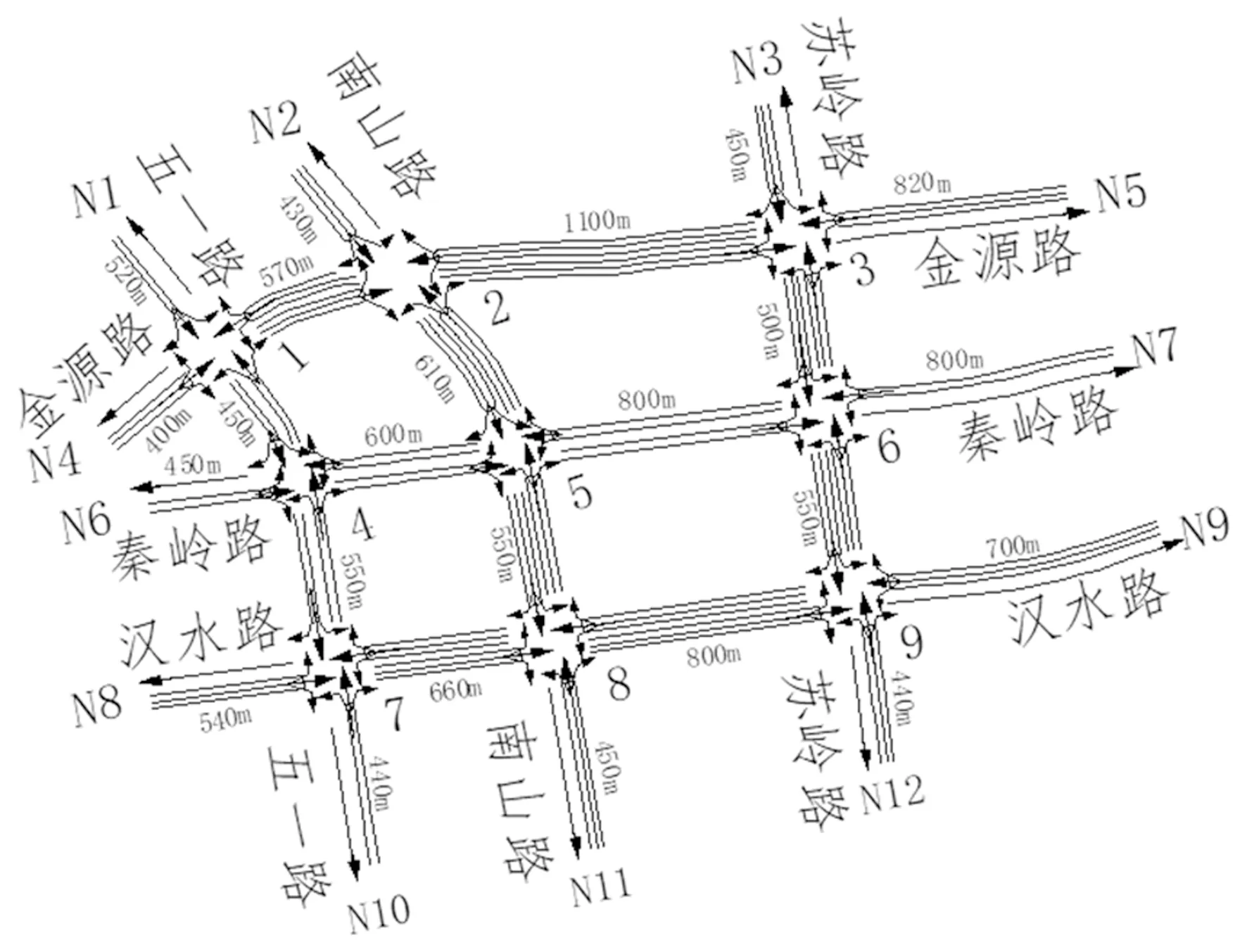
圖3 試驗控制區域路網

圖4 路網輸入流量隨時間變化曲線

2.2 結果分析

在給路網加載高峰小時的輸入流量后，用Webster定時控制方案對路網進行控制，路段上行駛車流密度隨時間變化曲線如圖5所示，圖例表示路段的名稱，例如X1-2表示從上游交叉口1到下游交叉口2的路段。從圖5中可以看出，路網中部分路段的單車道平均車流密度超過了40 veh·km-1，甚至達到了120 veh·km-1，表明該路段出現了堵塞，路網達到超飽和,擁堵路段密度的變化情況與文獻[4]中關于路段是否屬于堵塞區的車流密度范圍界定基本相符。

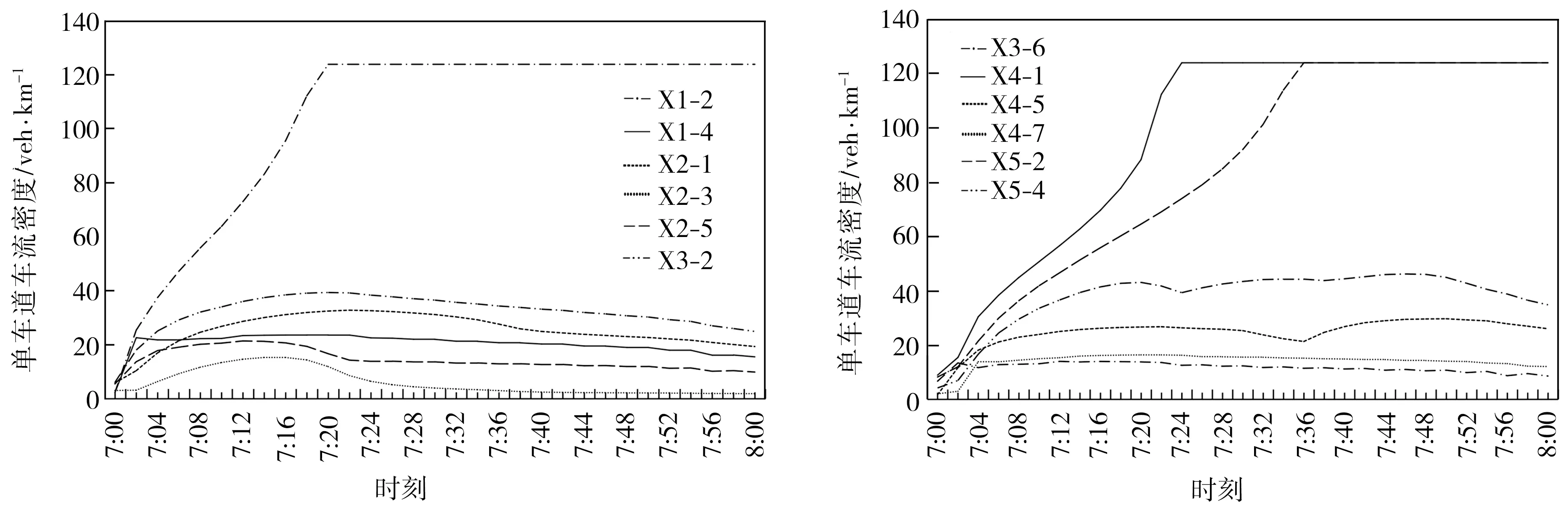
(a) 路段X1-2、 X1-4、X2-1、X2-3、X2-5、X3-2 (b)路段X3-6、 X4-1、X4-5、X4-7、X5-2、X5-4

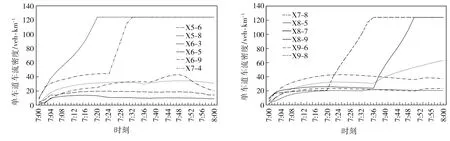
(c) 路段X5-6、 X5-8、X6-3、X6-5、X6-9、X7-4 (d) 路段X7-8、 X8-5、X8-7、X8-9、X9-6、X9-8

圖5 Webster定時控制下路段上行駛車流密度隨時間變化曲線圖

Fig.5 Traffic density curves of the road segment with time in Webster timing control

在運用優化控制模型計算最優的控制變量和狀態變量之前，首先要確定與該路網相適應的各路段最優車輛數累積量參照值(μmn)，確定原則如下：①由路段的長度和車道數計算初始車輛數累積量參照值μmn(0)，此時假設路網中的車輛數累積量均勻分布在各路段上，該車輛數累積量參照值的單車道平均密度取值范圍為60～70 veh·km-1，用上限計算初始車輛數累積量參照值μmn(0)=am-n×lm-n×70，其中am-n、lm-n分別表示上下游交叉口m、n連接路段的車道數和路段長度；②根據Webster定時控制模擬的路段擁堵情況，對擁堵路段的單車道平均密度進行適當的折減和調整，且單車道車流密度維持在20～40 veh·km-1范圍內，調整結果如表1所示。

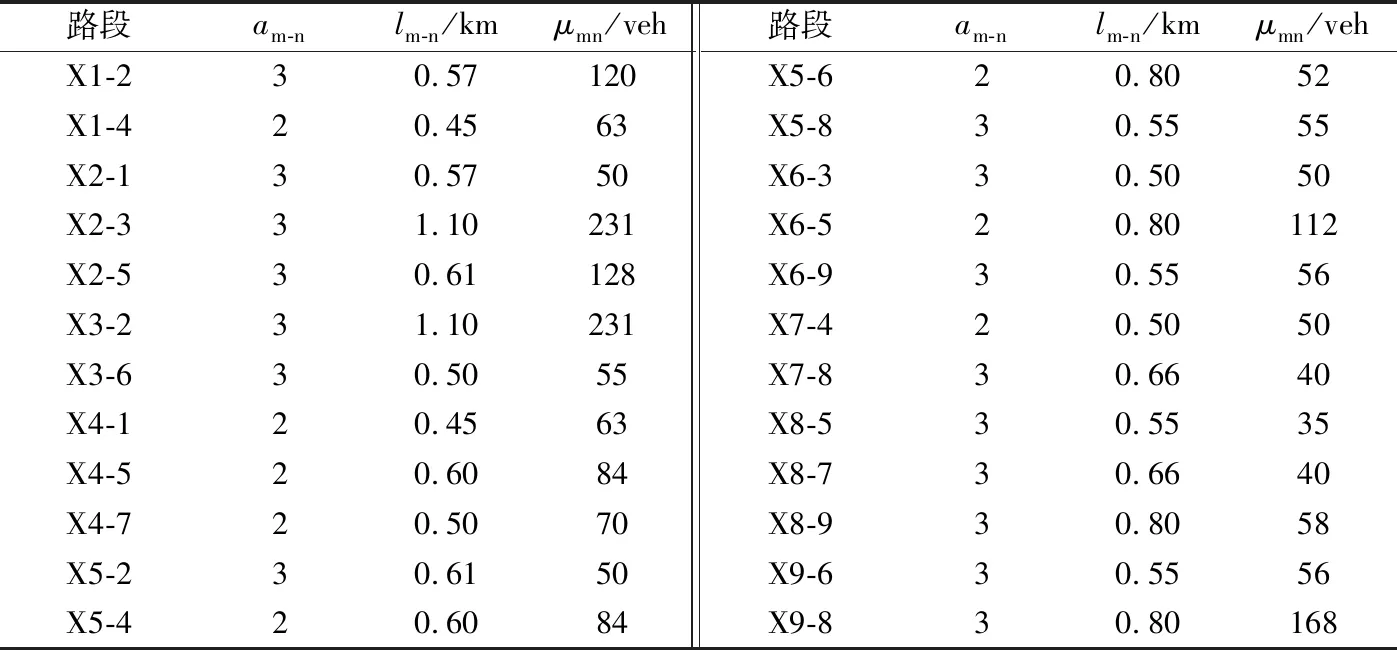
表1 路段車輛數累積量參照值調整結果

車輛數累積量參照值矩陣μ與路段車輛數矩陣的結構相同，將調整后的μ矩陣用于優化控制模型，模擬路網在相同外圍流量輸入下車流密度隨時間變化曲線圖如圖6所示。從圖6中可以看出，在模擬時間內路網中各路段的單車道平均流量基本保持穩定的狀態，絕大多數路段的單車道平均車流密度在40 veh·km-1以下，部分路段超過40 veh·km-1,但均保持在60 veh·km-1以下，其路段上的車流量保持在較高的輸出水平而不出現擁堵。由此表明，在模擬外圍輸入流量下，基于路段最優累積量參照的優化控制模型可以維持路網的穩定運行，避免控制區域發生擁堵。

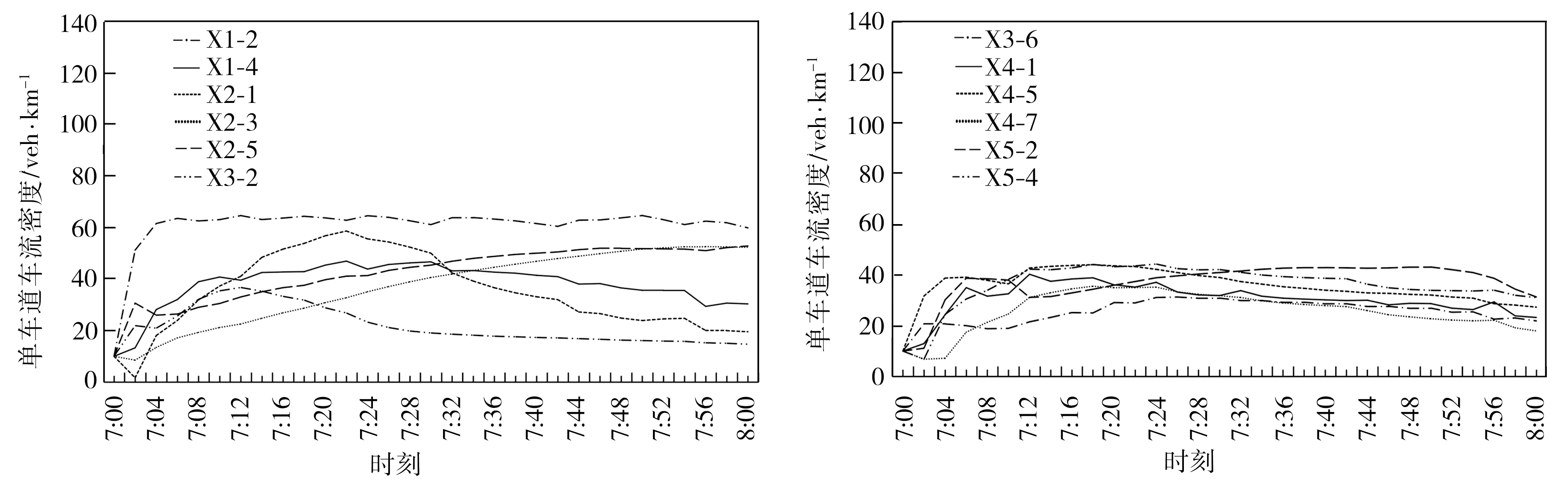
(a) 路段X1-2、 X1-4、X2-1、X2-3、X2-5、X3-2 (b)路段X3-6、 X4-1、X4-5、X4-7、X5-2、X5-4

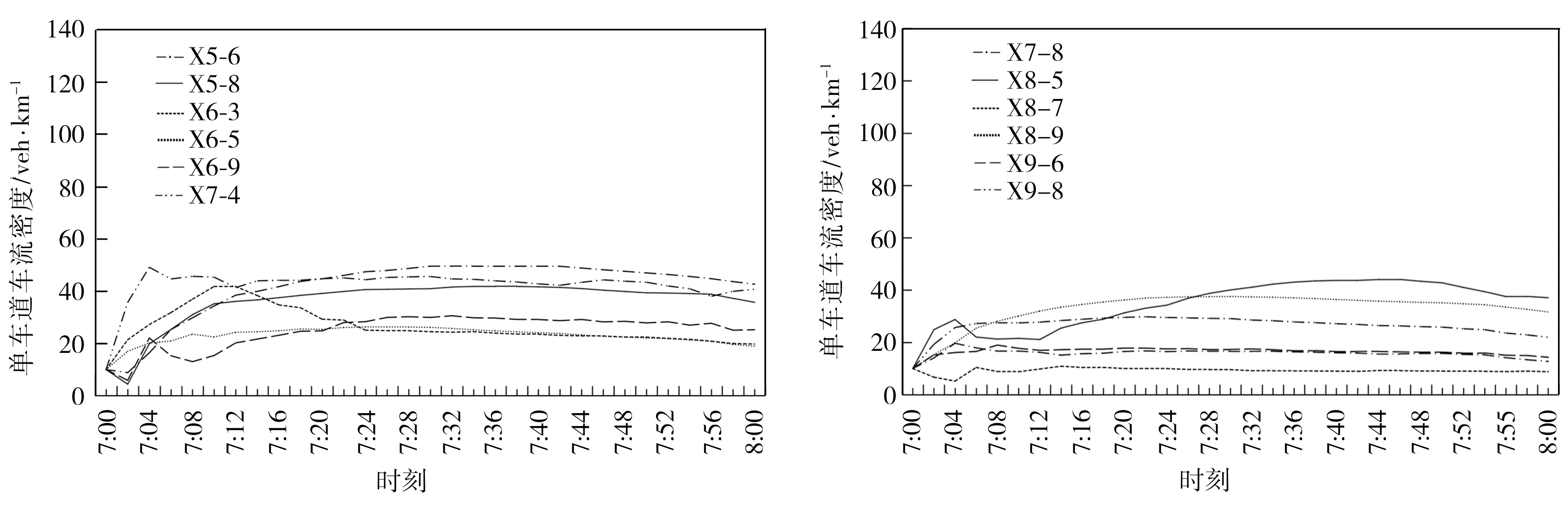
(c) 路段X5-6、 X5-8、X6-3、X6-5、X6-9、X7-4 (d) 路段X7-8、 X8-5、X8-7、X8-9、X9-6、X9-8

圖6 優化控制下路段上行駛車流密度隨時間變化曲線圖

Fig.6 Traffic density curves of the road segment with time in optimized control

將路網外圍的車輛輸入流量放大1.3倍后，用Webster定時控制方案和優化控制方案再次對路網進行控制并模擬路網中各路段的車輛數，不同輸入流量下路網車輛數變化趨勢如圖7所示。從圖7中可以看出，路網外圍車輛輸入流量放大1.3倍后，路網中車輛數變化與原流量輸入時車輛數變化趨勢一致，即優化控制方案下的路網累計輸入和累計輸出車輛數均比Webster定時控制方案下的累計輸入和累計輸出車輛數要大，而且優化控制方案下路段上車輛數累積量較Webster定時控制方案下車輛數累積量要小，由此表明，路網系統在優化控制方案下對車輛的輸出效率比在Webster定時控制方案下車輛的輸出效率高。

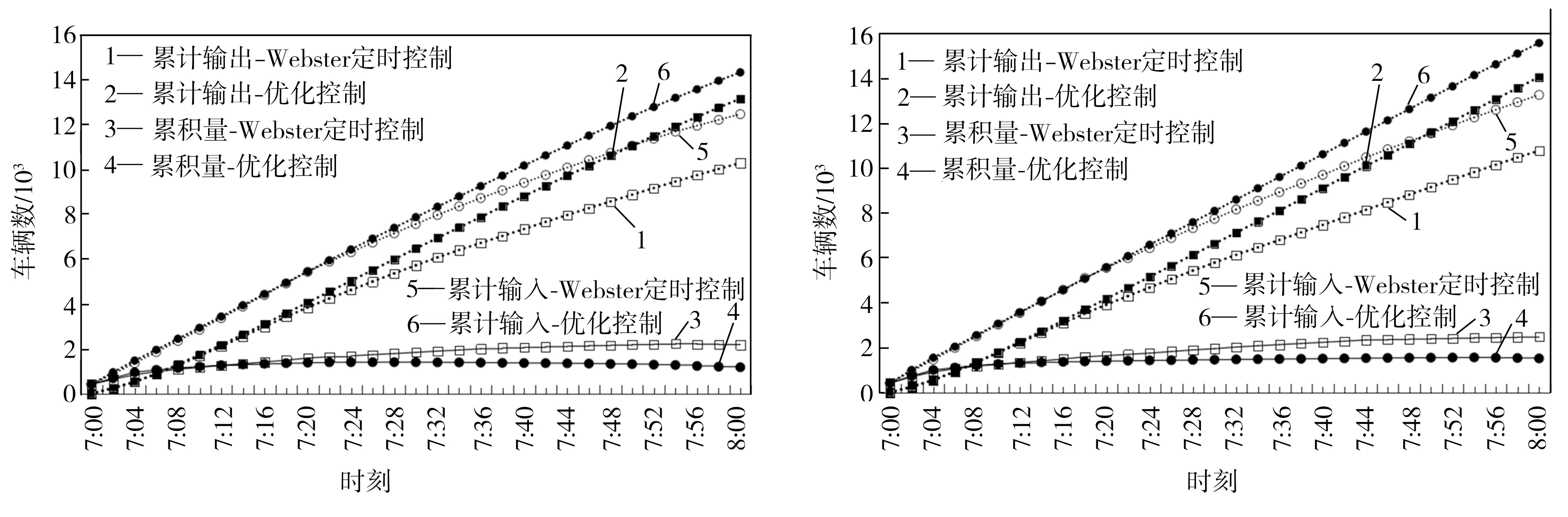
(a) 原流量輸入 (b) 輸入量放大1.3倍

圖7 不同輸入流量下路網車輛數變化趨勢

Fig.7 Variation trend of the number of vehicles in the road network at different input flows

不同控制方案下模擬高峰小時內路網累計輸出車輛數如表2所示。從表2中可以看出，在兩種高峰小時流量輸入下，在優化控制方案下的路網累計輸出車輛數明顯增加，與Webster定時控制方案相比，路網在優化控制方案下高峰小時內累計輸出率分別提高28.2%、30.43%。

表2 不同控制方案下模擬高峰小時內路網累計輸出車輛數

Table 2 Total number of output vehicles of road network during simulated peak hours with different control schemes

方案原高峰小時內累計輸出車輛數高峰小時輸入擴大1.3倍后累計輸出車輛數Webster定時控制10 20110 772優化控制13 07914 050

3 結語

基于交通流宏觀基本圖，優化控制模型以路網中路段累積車輛數作為控制目標，結合梯度投影法設計離散狀態的優化控制機制。與控制區域的Webster定時控制方案相比，運用優化控制策略在一定程度上可以避免控制區域中的路段出現擁堵，同時增加路網的輸入和輸出車輛數，從而使路網整體輸出效率得到明顯提升。