基于ESO的攔截機動目標帶攻擊角度約束制導律

張寬橋,楊鎖昌,劉 暢

(陸軍工程大學 石家莊校區導彈工程系,河北 石家莊 050003)

在現代戰爭中,很多導彈需要以一定的攻擊角度命中目標,來增加戰斗部的毀傷效能。1973年,KIM首次將攻擊角度約束問題引入制導律設計中。其后經過40多年的發展,針對帶攻擊角度約束制導律的研究成果豐碩[1]。由于滑模變結構控制在滑動模態對干擾具有不變性,因此被廣泛應用在制導律設計中。文獻[2]采用彈目視線角速率和攻擊角度約束項作為滑模面,結合自適應指數趨近律,設計了帶攻擊角度約束的滑模制導律。

傳統滑模制導律采用線性滑模面,不能使系統狀態有限時間收斂至平衡點,而終端滑模控制能使系統狀態有限時間收斂[3]。文獻[4]基于終端滑模控制,提出了帶攻擊角度約束的有限時間收斂制導律,使系統狀態有限時間收斂至平衡點,但制導指令中含有負指數項,會存在奇異問題。文獻[5]改進了一種非奇異終端滑模面函數,解決了奇異問題,提出了非奇異終端滑模控制方法。文獻[6]基于非奇異終端滑模控制,提出了帶攻擊角度約束的制導律。文獻[7]進一步提出了一種快速收斂的非奇異終端滑模面,具有比傳統非奇異終端滑模更快的收斂速度。

導彈自動駕駛儀并非一個理想環節,它存在延遲等動態特性,會一定程度上影響導彈的制導性能,因此在制導律的設計中需要加以考慮。文獻[8]將自動駕駛儀近似為一階環節,基于非奇異終端滑模控制和動態面控制來設計制導律,具有良好的制導性能。實際上,導彈自動駕駛儀一般具有高階動態特性。若將其近似為高階環節,能夠很好地模擬駕駛儀的動態特性,但這會使制導律的形式過于復雜。為解決這個問題,有學者將駕駛儀近似為二階環節,在貼近駕駛儀實際動態特性的同時,降低制導律形式的復雜程度。文獻[9]考慮導彈自動駕駛儀二階動態特性,基于動態面控制設計制導律,并未考慮攻擊角度約束問題。

本文針對攻擊角度約束的問題,選取了一種帶攻擊角度約束項的非奇異快速終端滑模面,將導彈自動駕駛儀動態特性近似為二階環節,提出了帶攻擊角度約束的新型制導律。該制導律不但克服了文獻[4]中制導律存在的奇異問題,還提高了系統狀態的全局快速收斂性,實現了對自動駕駛儀動態特性的有效補償。針對目標加速度未知的問題,本文還設計了超螺旋擴張狀態觀測器對目標加速度進行估計。仿真表明,所設計制導律能夠滿足命中精度和攻擊角度約束的要求。

1 彈目相對運動模型

假設導彈和目標均為質點,在二維慣性坐標系上建立彈目相對運動幾何關系圖,如圖1所示。圖中,vm和vt為導彈和目標的速度,假設為常值;θm和θt為導彈的彈道傾角和目標的航跡傾角;r為彈目相對距離,q為彈目視線角。

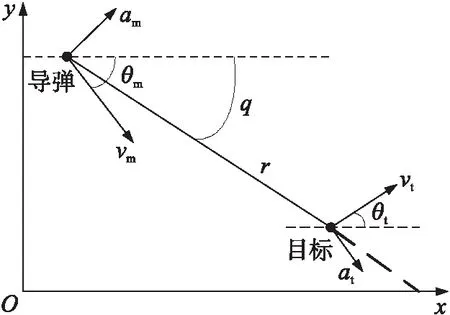
圖1 彈目相對運動關系

因此,可構建彈目相對運動方程為

(1)

(2)

(3)

(4)

式中:ηm=q-θm,ηt=q-θt。

對式(2)求導,并結合式(1)得:

(5)

式中:atq=atcosηt,視為有界未知量來處理。

攻擊角度為導彈擊中目標時導彈與目標速度矢量方向之間的夾角,攻擊角度約束問題可以轉化為終端視線角約束問題。自動駕駛儀的動態特性對導彈的制導效果有很大的影響,需要加以考慮。導彈自動駕駛儀可用二階動態特性來描述[10],表達式為

(6)

式中:ξ為導彈自動駕駛儀的阻尼比,ωn為自振頻率,ac為導彈制導指令。

考慮自動駕駛儀動態特性帶攻擊角度約束的彈目相對運動模型可描述為

(7)

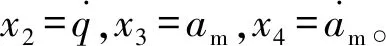
2 超螺旋擴張狀態觀測器

在制導過程中,目標的加速度信息往往是無法進行測量的,因此需要對目標機動等信息進行估計。擴張狀態觀測器(extended state observer,ESO)是一種很好的估計系統不確定性的方法[11]。但傳統的ESO在設計時,將總擾動視為常值或者是慢變的量,故總擾動的導數為0。在估計時變擾動的時候,這種處理方式阻礙了ESO性能的進一步提升。雖然針對時變的干擾,可以增大ESO的增益來獲得滿意的干擾估計效果。但是,當系統的輸出存在測量噪聲時,高增益會帶來測量噪聲的放大問題。借鑒ESO設計思想,將二階滑模超螺旋算法[12]與ESO相結合設計一種超螺旋擴張狀態觀測器(STESO),具有ESO和滑模控制的優點,且采用超螺旋算法能夠降低滑模控制的抖振現象。

考慮如下一階系統:

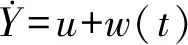
(8)

式中:Y為系統輸出,u為系統輸入,w(t)為總擾動。

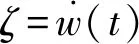
|ζ|≤ζu

(9)

式中:ζu為ζ的上界。

定義新的狀態變量y1=Y,y2=w(t),則式(8)可描述為

(10)

基于超螺旋算法改進擴張狀態觀測器,在超螺旋算法中引入了線性項,進一步加快觀測器的收斂速度,設計STESO為

(11)

結合式(10)和式(11)可得:

(12)

為證明方便,引入如下引理。

針對如下非線性系統:

(13)

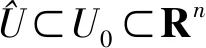
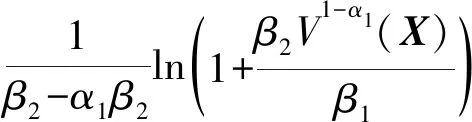
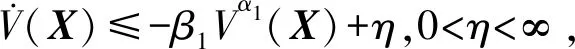
證明定義一組新的狀態變量:

(14)

微分得:

(15)

式中:

(16)

定義Lyapunov函數:

V1=YTPY

(17)

(18)

易證P為正定矩陣,則下式成立:

λmin(P)‖Y‖2≤V1≤λmax(P)‖Y‖2

(19)

式中:λmax(P)和λmin(P)為矩陣的最大和最小特征值。

對式(17)微分得:

(20)

式中:

(21)

易證Q1為正定矩陣。由式(16)和式(18)可得:

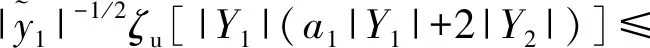
(22)

定義Q=Q1+Q2,將式(22)代入式(20)得:

(23)

式中:

(24)

選取如下參數:

(25)

易證Q為正定矩陣。

由式(19)可知:

(26)

式(23)可轉化為

(27)

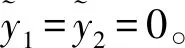
針對式(5)可以建立如下STESO:

(28)

式中:z2為atq/r的估計值。

3 帶攻擊角度約束制導律

(29)

式中:k1>0,k2>0,α=p1/p2>1,β=p1/p2,1<β<2,p1、p2、p3、p4均為奇數。

當系統到達滑模面后,即:

(30)

則x1和x2可有限時間收斂至原點,且比傳統非奇異終端滑模的收斂速度更快。具體證明參考文獻[7]。

為削弱抖振,同時加快滑模趨近速率,增強制導律的自適應性,選取如下指數冪次趨近律:

(31)

式中:k3>0,k4>0,γ>0。

相比傳統的指數趨近律,趨近律(31)的系數可隨彈目距離的變化而自適應地調整。當彈目距離較大時,趨近律系數較小,制導指令較小,保證了導彈的飛行穩定性;彈目距離逐漸減小時,系數增大,收斂速度加快,保證了制導精度的要求。

定理2基于滑模面(29)和趨近律(31),利用STESO對目標加速度信息進行估計,采用動態面控制方法設計考慮導彈自動駕駛儀動態特性的攻擊角度約束制導律為

(32)

x3c和x4c為虛擬控制指令,τ3和τ4為濾波器的時間常數,τ3>0,τ4>0,則滑模面S1能在有限時間內收斂至區域|S1|≤δ,其中δ為一較小正數。同時系統狀態x1和x2能夠在有限時間內收斂至區域:

(33)

證明定義邊界層誤差:

σi=xid-xic,i=3,4

(34)

微分得:

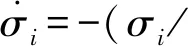
(35)

選取Lyapunov函數:

(36)

微分得:

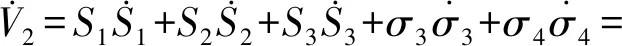
(37)

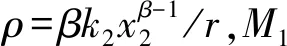
將式(37)整理后得:

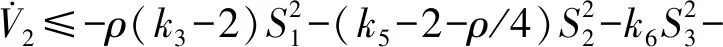
(38)

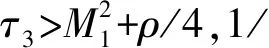
(39)

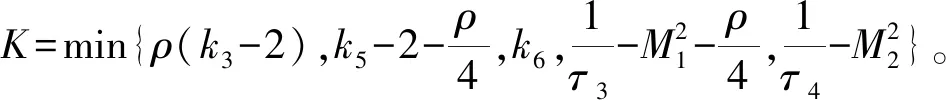
求解式(39)得:

0≤V2(t)≤1/(4K)+[V2(0)-1/(4K)]e-2Kt

(40)

由式(40)和引理3可知,V2是有限時間穩定且有界的,因此,S1、S2、S3、σ3和σ4是有界的。若參數選擇適當,可使它們任意小。因此必然存在一個較小正數δ,使得在制導律(32)的作用下,滑模面S1可在有限時間內收斂至區域|S1| ≤δ。當S1進入區域|S1| ≤δ,令S1=κ,其中|κ| ≤δ,可得:

(41)

式(41)可進一步寫成:

(42)

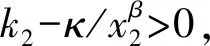
|x2|≤(|κ|/k2)1/β≤(δ/k2)1/β

結合式(41)可得x1能夠有限時間內收斂至區域:

|x1|≤|x1|+k1|x1|α≤k2|x2|β+|κ|≤2δ

證畢。

制導律(32)中存在x3d和x4d需要根據式(32)進行求解。比較k5和1/τ3、k6和1/τ4的參數取值范圍,可以發現其取值范圍基本重合,因此可以令k5=1/τ3,k6=1/τ4,此時既可以消去制導律(32)中的x3d和x4d項,又可以減少制導律中的參數數量,且不影響其整體性能。簡化后的制導律形式為

(43)

為敘述方便,將式(43)所示的考慮自動駕駛儀動態特性的滑模制導律簡記為ADNTSMG。

4 仿真分析

本節基于彈道仿真,對所設計制導律的性能進行對比仿真研究。導彈和目標的初始位置分別為(0,0)和(15 km,10 km),導彈的速度為vm=800 m/s,初始航跡角θm=45°,目標運動速度vt=300 m/s,初始航跡角θt=180°。導彈過載n=am/g,導彈的最大可用過載為20。設置自動駕駛儀動態參數為ξ=0.8,ωn=8 rad/s。仿真中引入了文獻[2]提出的自適應滑模制導律(ASMG)以及文獻[6]提出的非奇異終端滑模制導律(NTSMG)進行對比仿真。為驗證STESO的性能,引入傳統ESO進行對比仿真分析。

根據目標圓弧機動和蛇形機動2種機動方式,分2種情形進行仿真。其中圓弧機動時,at=10 m/s2,蛇形機動時,at=20sin(πt/5)。仿真結果如圖2～圖6和表1所示,表中,tf為攻擊時間,D為脫靶量。

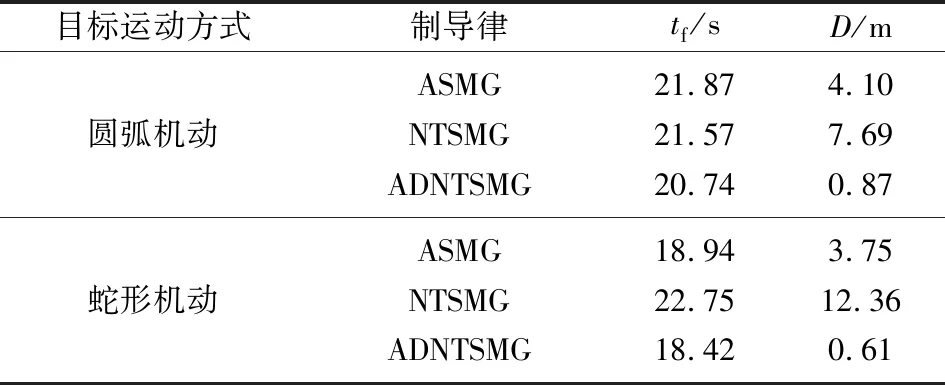
表1 攻擊時間和脫靶量的仿真結果

圖2為目標加速度的估計曲線,可以看出,STESO相比傳統ESO能夠更快、更準確地對目標的加速度信息進行實時在線估計,具有較快的收斂特性和較強的魯棒性。

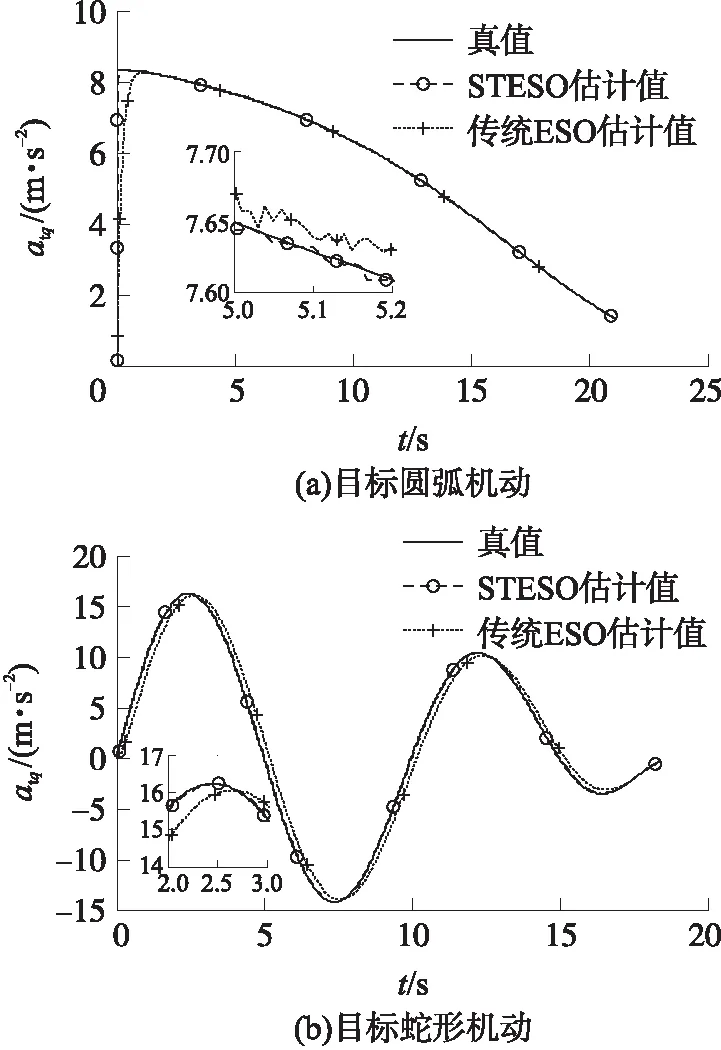
圖2 目標加速度估計

由圖3可以看出,在ADNTSMG作用下,導彈的運動軌跡較為光滑,在末段較為平直,這是由于ADNTSMG采用了非奇異快速終端滑模面,使得彈目視線角速率能夠在有限時間內快速收斂至0附近。在ASMG的作用下,導彈運動軌跡的曲率整體較大。在NTSMG的作用下,導彈的運動軌跡在制導末段曲率變化較為劇烈。

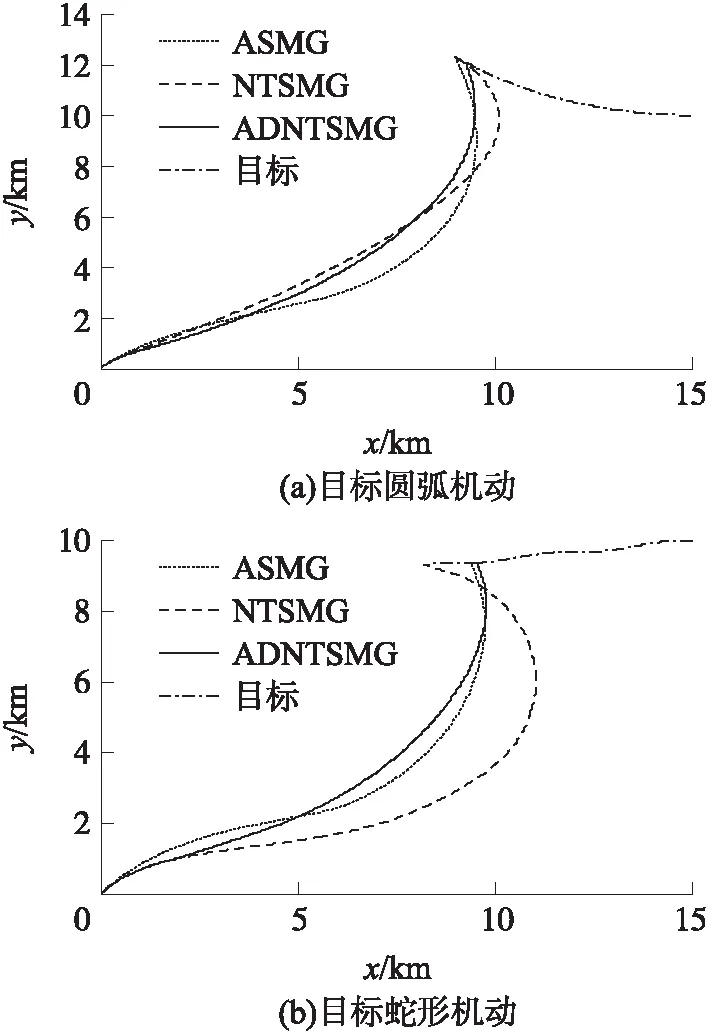
圖3 彈目運動軌跡

由圖4可知,ASMG和ADNTSMG能使彈目視線角收斂至90°附近,但ASMG存在抖振和發散現象,主要由于滑模制導律固有的抖振問題和自動駕駛儀動態特性的影響。而ADNTSMG對自動駕駛儀動態特性進行補償且采用了自適應指數趨近律削弱了抖振現象。NTSMG彈目視線角不能達到期望角度,且逐漸發散。

由圖5和圖6可以看出,ASMG和NTSMG均不能使彈目視線角速率及導彈過載收斂至0附近,且有抖振現象和發散趨勢,這將增大導彈的脫靶量(見表1)。而ADNTSMG能使彈目視線角速率及導彈過載有效收斂至0附近。ADNTSMG在末端需用過載較小,有足夠的過載余量應對各種干擾,進而能提高導彈的制導精度(見表1)。由表1可以看出,ADNTSMG的攻擊時間和脫靶量明顯小于ASMG和NTSMG。

綜上所述,ADNTSMG能補償自動駕駛儀動態特性,攻擊時間和脫靶量均小于ASMG和NTSMG,且彈目視線角及角速率能有限時間內收斂至期望值附近,驗證了ADNTSMG的有效性及優越性。

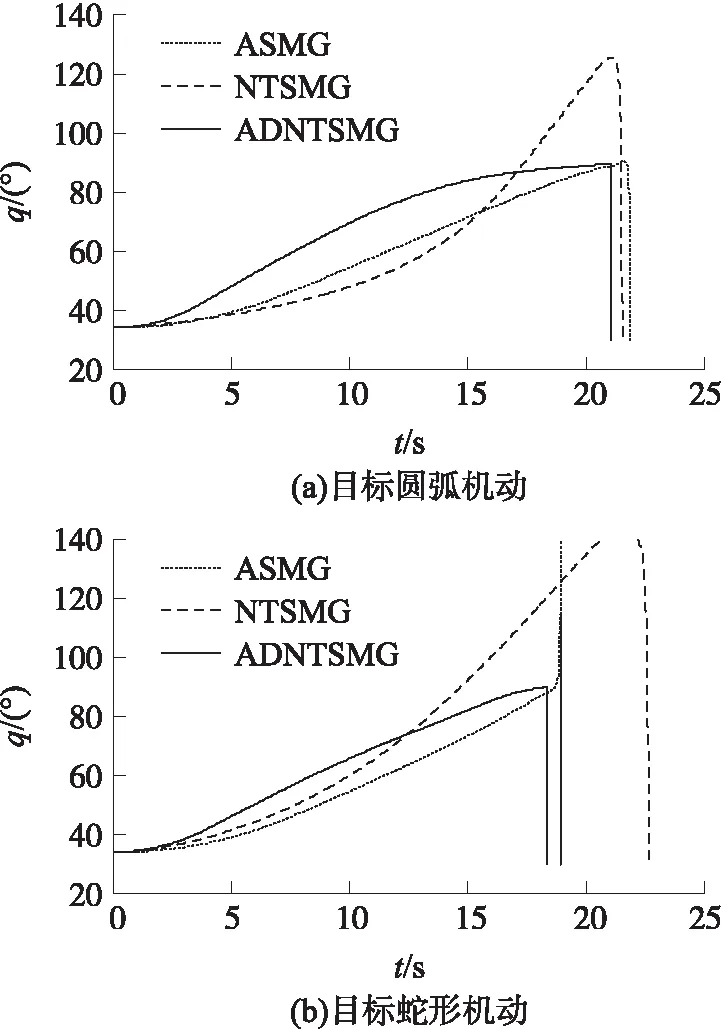
圖4 彈目視線角

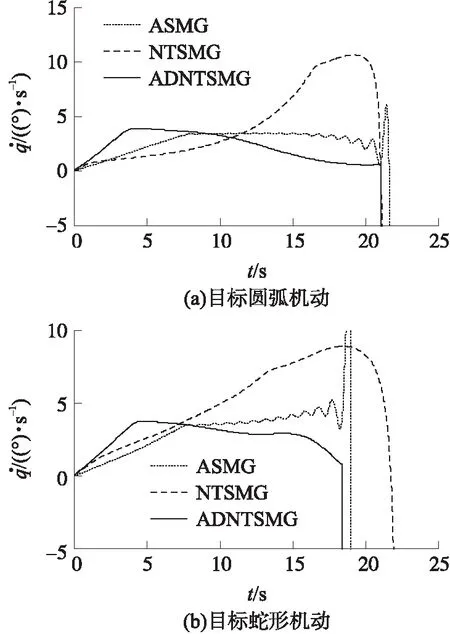
圖5 彈目視線角速率

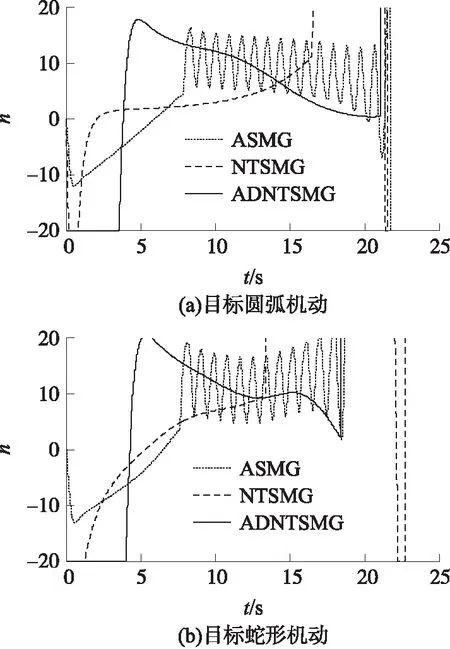
圖6 導彈法向過載

5 結束語

本文針對攻擊角度的問題,提出了一種帶攻擊角度約束考慮自動駕駛儀動態特性的滑模制導律。通過理論分析和仿真驗證,可以得出以下結論:

①快速收斂的非奇異終端滑模面,能夠實現制導系統狀態有限時間快速收斂,自適應指數趨近律能削弱抖振,增強滑模控制的自適應性。

②超螺旋擴張狀態觀測器STESO估計精度高,收斂速度快,能有效估計系統未知干擾。

③考慮自動駕駛儀動態特性的制導律ADNTSMG能夠對自動駕駛儀動態特性進行有效補償,增強制導系統的魯棒性,提高導彈的制導性能。

制導參數的選取會影響制導律的制導性能,后續還需要針對制導參數優化方面進行研究。