永磁同步電機氣隙磁場定向控制仿真分析

張慶宇，涂群章，周建波，蔣成明

(中國人民解放軍陸軍工程大學， 南京 210007)

當前，在電驅動工程車輛中，由于永磁同步電機具有結構簡單、運行可靠、體積小、效率高等優(yōu)勢而成為車輛驅動電機的首選，而控制技術是直接影響著永磁同步電機工作性能發(fā)揮，成為永磁同步電機技術的關鍵。目前永磁同步電機控制技術主要有：轉子磁場定向控制，定子磁場定向控制[1]。但是這些方法在一些工況下不能得到良好的控制效果：轉子磁場定向控制受轉子參數(shù)變化影響較大，一定程度上影響系統(tǒng)性能；實物電機受工藝限制，產(chǎn)生大量磁場諧波，定子磁場定向控制氣隙旋轉磁鏈受諧波影響較大[2]。

在非線性的磁場中，磁飽和效應嚴重影響高性能電機的驅動系統(tǒng)控制精度。電機運行過程中，定子電流會隨負載而變化，當電動機負載加大時，定子電流也會加大，電動機氣隙磁場出現(xiàn)飽和[3]。而由于磁鏈和電流關系中存在耦合，由于磁路的飽和程度與氣隙磁通一致，基于氣隙磁鏈的控制方式更適合處理電機磁場飽和效應[4]。

永磁同步電機產(chǎn)生氣隙磁場的源有兩個：一個是定子電流；另一個是轉子上的永磁體。定子電流產(chǎn)生的氣隙磁場分析方法同感應電機相同。轉子上的永磁體可等效成磁動勢源[5]。

勵磁同步電機氣隙磁場定向控制建立了定子勵磁電流is與轉子勵磁電流if在電機MT旋轉坐標系下的數(shù)學模型，得到ism、ist、ifm、ift，合成氣隙磁鏈ψg[6]。永磁同步電機定子磁場定向控制將定子磁鏈ψs建立在MT旋轉坐標系中，其與氣隙磁鏈定向控制的區(qū)別在于沒有考慮電樞漏磁鏈[7]。

本文給出了基于氣隙磁場定向的永磁同步電機矢量控制模型，將氣隙磁鏈ψg建立在MT旋轉坐標系中，得到的iM與iT值經(jīng)過坐標變換，空間矢量脈沖寬度調制(SVPWM)對電機進行控制[8]。在Matlab/SimuLink進行仿真分析，基于氣隙磁場定向控制的永磁同步電機具有良好的動態(tài)及穩(wěn)態(tài)特性，為下一步的工程設計提供理論基礎。

1 永磁同步電機數(shù)學模型分析

在建立永磁同步電機模型前需要進行假設[9]：忽略定、轉子鐵心磁阻與阻尼磁阻，永磁材料電導率與磁導率的影響。

1.1 考慮磁場諧波分析的電機模型分析

建立d-q同步旋轉坐標系，永磁同步電機轉子方向與d軸方向一致，q軸垂直與轉子方向，d-q坐標系的數(shù)學模型如圖1。

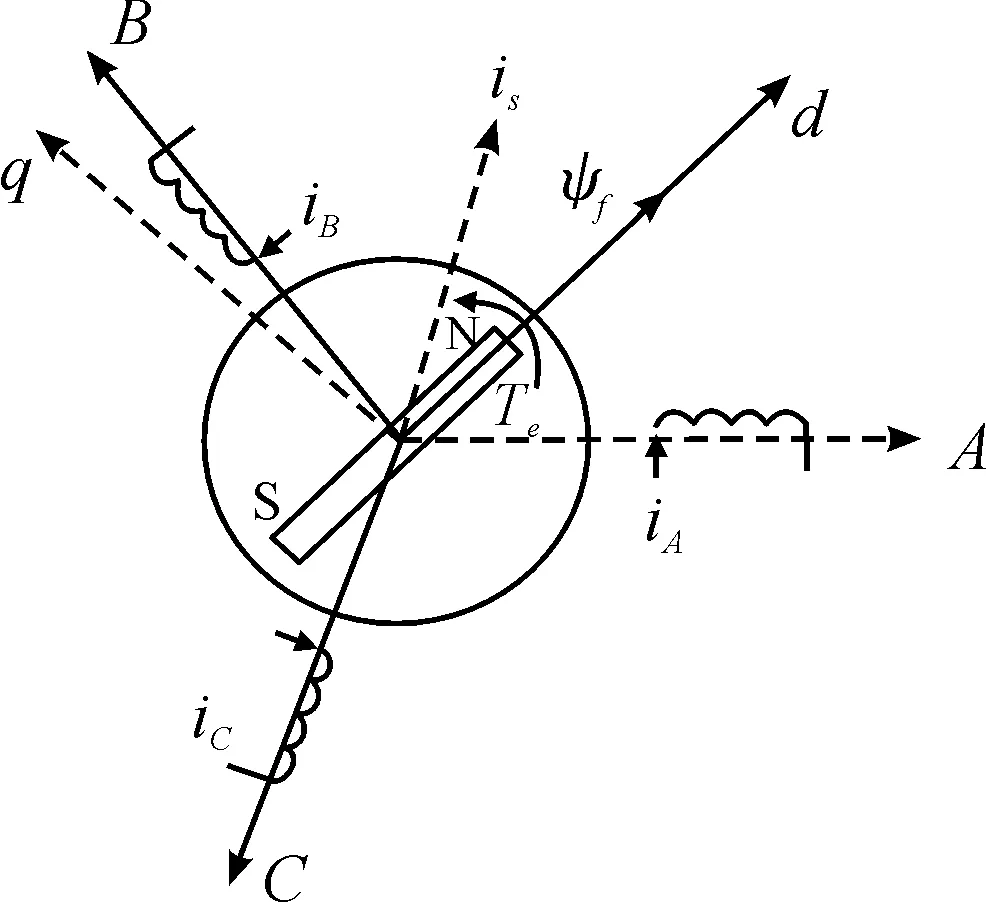
圖1 永磁同步電機dq坐標系下的數(shù)學模型示意圖

dq坐標系下定子電壓方程為

(1)

d、q軸磁鏈方程為

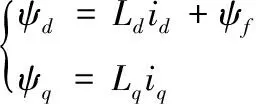
(2)

此時的電磁轉矩方程為

(3)

其中， 永磁同步電機參數(shù)如表1所示。

表1 永磁同步電機參數(shù)

實物電機受工藝限制，無法完全按照理想電機一樣輸出理想波形，永磁同步電機產(chǎn)生的磁場中含有大量諧波，使得電機的氣隙磁場并非理想正弦分布[10-11]，在d、q坐標系下產(chǎn)生的磁鏈方程為

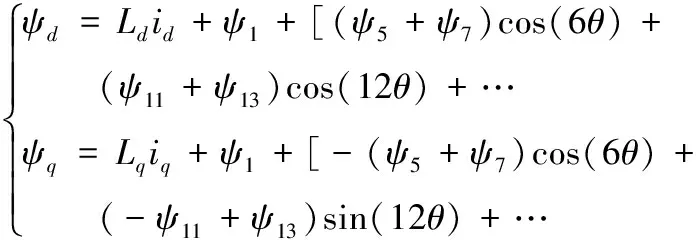
(4)

電磁轉矩方程為

[ψd6sin(6θ)+ψd12sin(12θ)+…]id+

[ψq6cos(6θ)+ψq12cos(12θ)+…]iq}

(5)

1.2 氣隙磁場定向控制模型分析

建立MT同步旋轉坐標系，永磁同步電機氣隙磁鏈方向與M軸方向一致，T軸垂直于氣隙磁鏈方向。MT坐標系的數(shù)學模型如圖2所示。

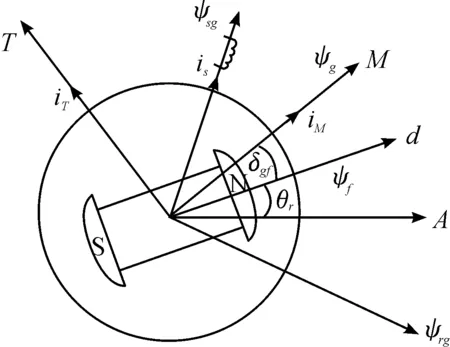
圖2 氣隙磁場定向控制模型示意圖

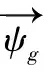
(6)

ψsg=Lmis

(7)

聯(lián)立式 (3)、式(4)得：

(8)

(9)

θs為is在MT軸系中的相位。

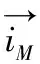
Te=pψgiT

(10)

2 永磁同步電機控制系統(tǒng)分析

2.1 氣隙磁鏈觀測器設計

求解MT坐標系、d-q坐標系、ABC坐標系下各物理量之間的矢量關系，建立氣隙磁場定向控制矢量圖，如圖3所示。A軸與d軸之間角度為θr，d軸與M軸之間角度為δgf，則可以利用坐標系變化得到MT軸系下的物理量。

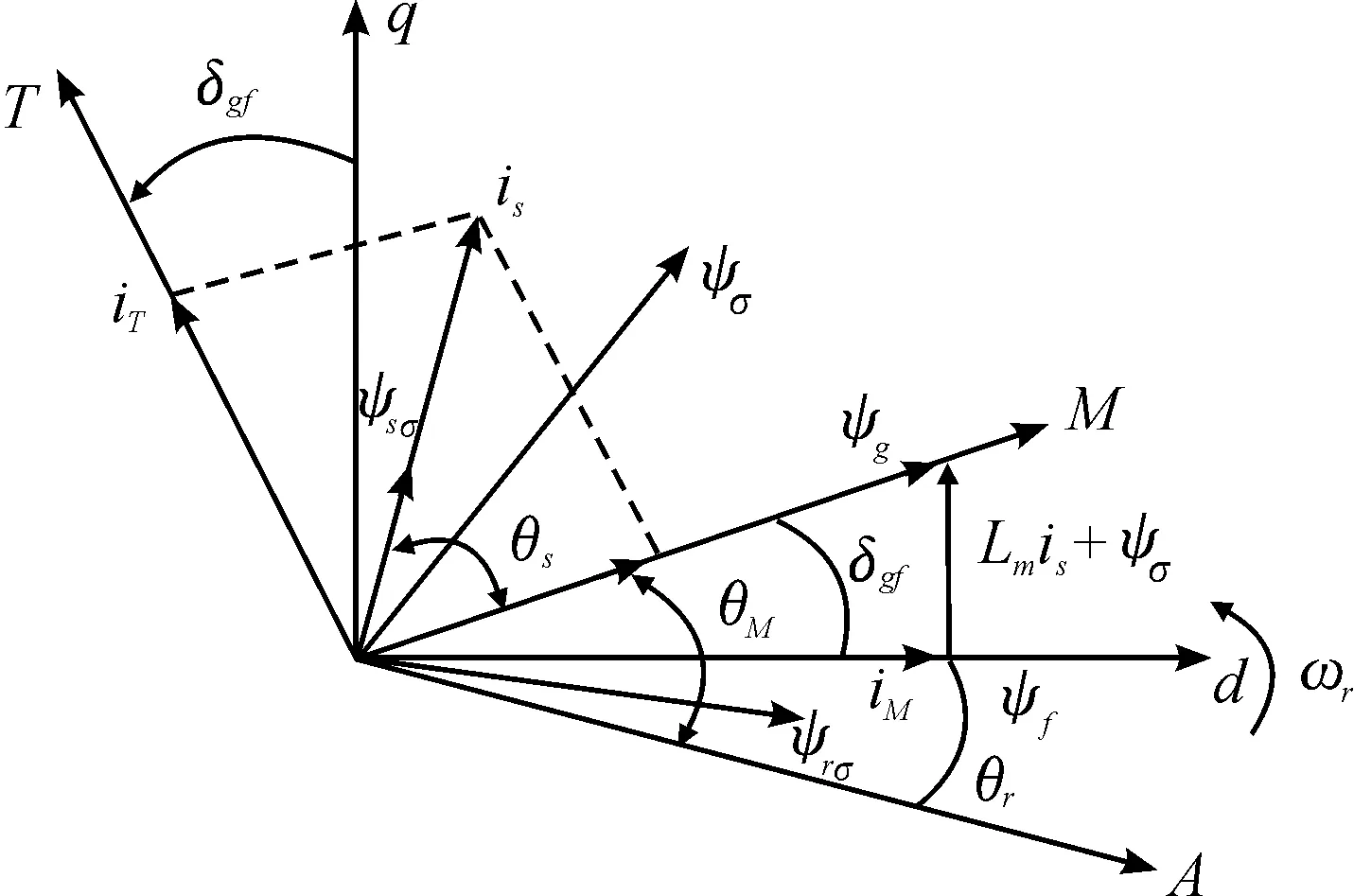
圖3 氣隙磁場定向的矢量圖

氣隙磁鏈矢量方程為

(11)

氣隙磁鏈標量方程為

(12)

其MT軸系構成的氣隙磁估算器結構如圖4所示。

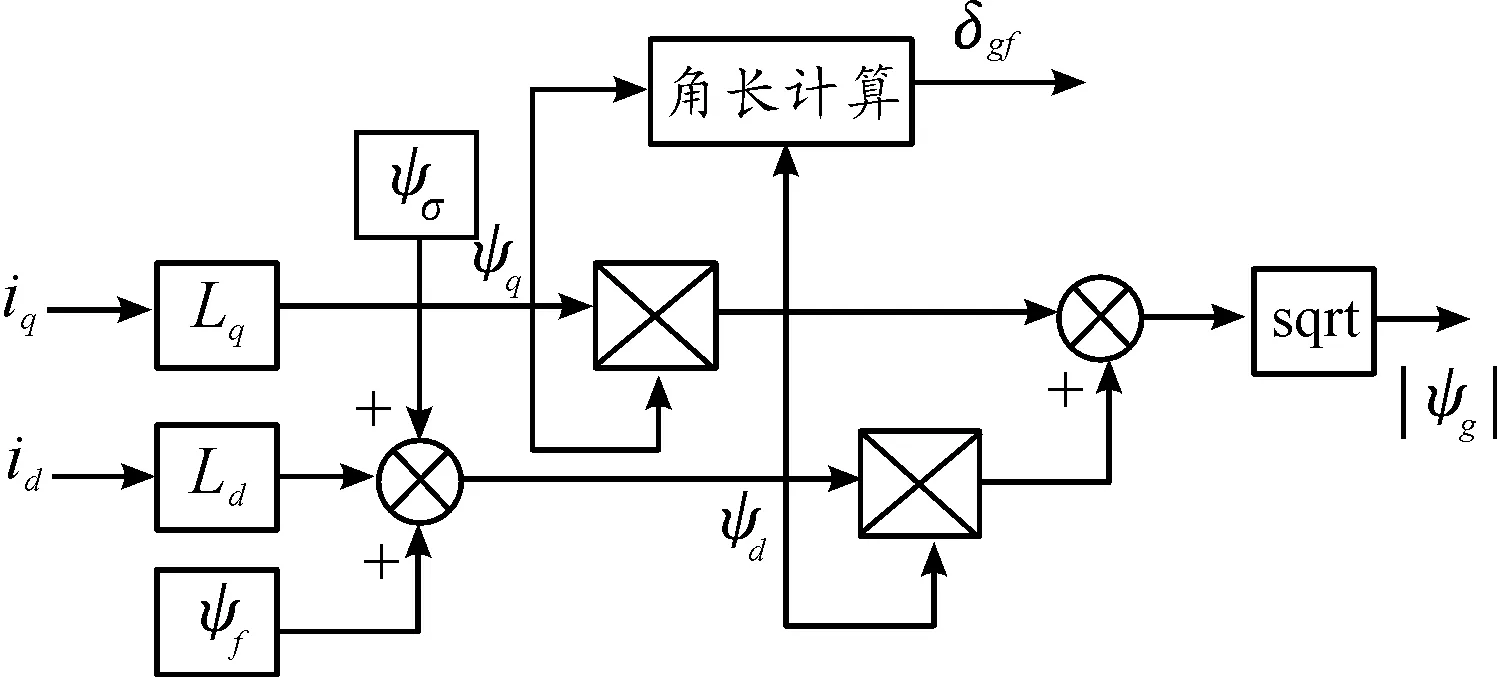
圖4 氣隙磁鏈觀測器結構框圖

MT坐標系中電壓方程為

(13)

MT軸系沿氣隙磁場定向，則ψT=0,ψM=ψg，則

(14)

uT=RsiT+ωsψg

(15)

2.2 基于電機模型的查表法

利用永磁同步電機氣隙磁場定向控制的數(shù)學方程，通過給定的電磁轉矩和氣隙磁鏈得到iM與iT值。具體思路為聯(lián)立方程式(9)、式(12)，通過離線計算方法[12-13]得到參考值iM與iT。其實現(xiàn)方法為:

1) 通過設定轉矩參考值為特定值Ti，確定與Ti對應的iTi值工作范圍M=(0,is_max)，選擇M范圍內n個等距點作為iT測量點iTi=[iT1,iT2,…iTn](iT1≤iT2≤…≤iTn)

2) 將iTi、Ti代入式(9)得到iMi=[iM1,iM2,…,iMn]。

3) 將得到的iTi、iMi合并成矩陣：

(ITi,IMi) =[(IT1,IM1),(IT2,IM2),…,(ITn,IMn)]

(16)

將MT軸電流組合向量(ITi,IMi)代入氣隙磁鏈式(13)得到氣隙磁鏈ψgi=[ψgi1,ψgi2,…,ψgin]。

4) 經(jīng)過上述3步后，設定轉矩值為Ti+1，重復上述步驟，最后得到完整二維表格。利用(ITi,IMi,Ti,ψgi)矩陣建表，表格結構如表2所示，每一行代表相同轉矩參考值的(ITi,IMi)值，每一列代表相同磁鏈參考值的(ITi,IMi)值。

表2 表格結構

5) 將得到的數(shù)據(jù)代入電流查表模塊，電流查表依據(jù)線性插值得到任一轉矩、磁鏈下對應的iM、iT值。

利用公式法或查表法均可得到iM、iT，查表法雖然在建立表格的過程中略微復雜，但是一旦表格建立完畢，查表算法按照二維線性插值，更加簡單，計算量大為減少。

氣隙磁場定向在基于轉子磁場定向的基礎上進行修正，由磁通估算器得到氣隙磁鏈，由電流在線查表得到iT、iM值，則永磁同步電機氣隙磁場矢量控制系統(tǒng)簡圖如圖5所示。

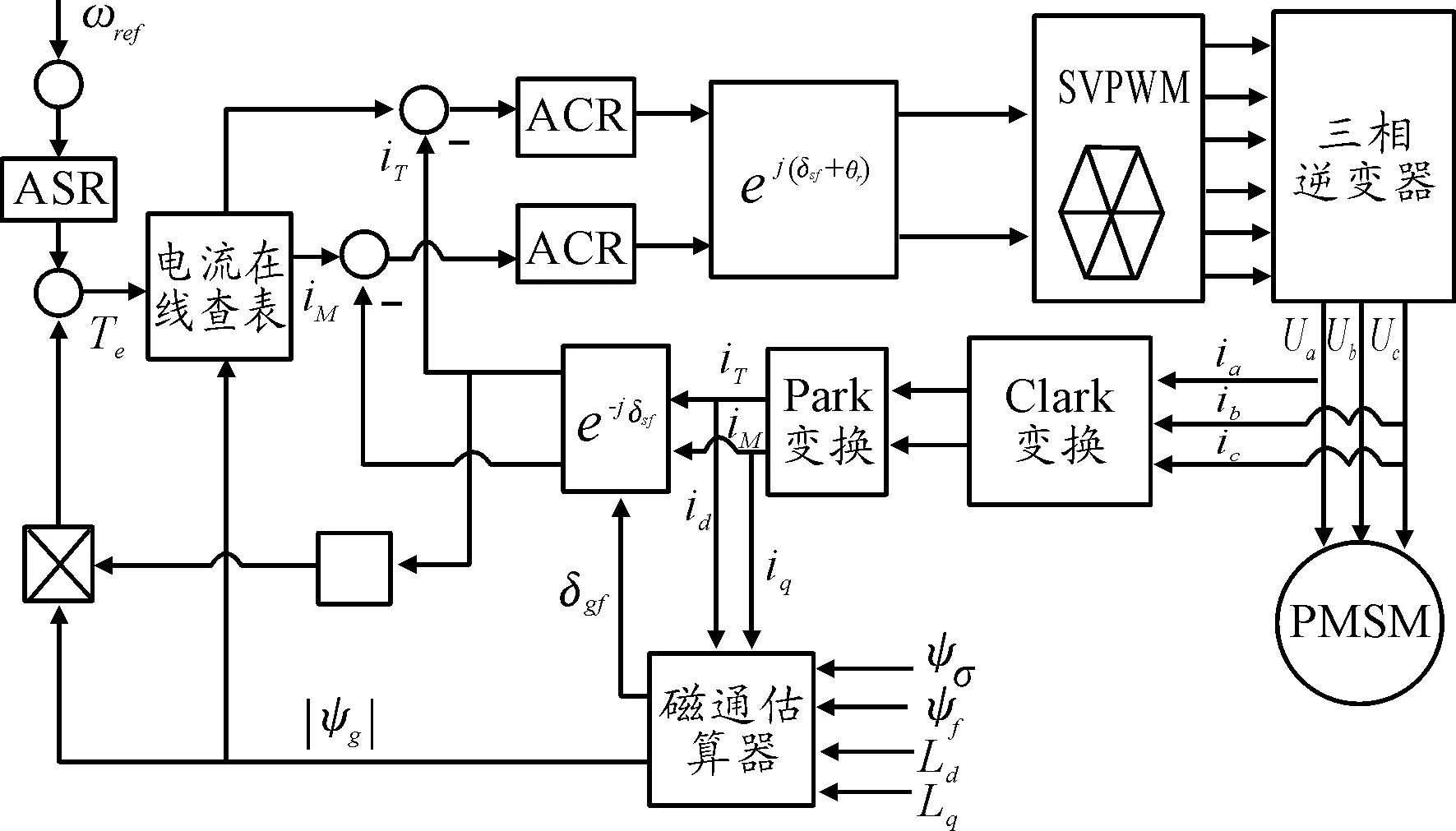
圖5 永磁同步電機控制系統(tǒng)簡圖

從圖5可以看出，永磁同步電機輸入轉速經(jīng)轉速調節(jié)器調節(jié)后得到轉矩值Te，反饋信號經(jīng)磁通估算器得到氣隙磁鏈幅值|ψg|。Te、|ψg|經(jīng)電流在線查表得到iT、iM值，通過坐標變換和空間脈沖寬度調制(SVPWM)實現(xiàn)電機控制。反饋信號經(jīng)坐標變換得到iT、iM值形成閉環(huán)控制回路。

3 控制系統(tǒng)仿真分析

在Matlab/Simulink中搭建永磁同步電機氣隙磁場控制仿真模型，仿真模型如圖6所示，其仿真電機參數(shù)如表3。

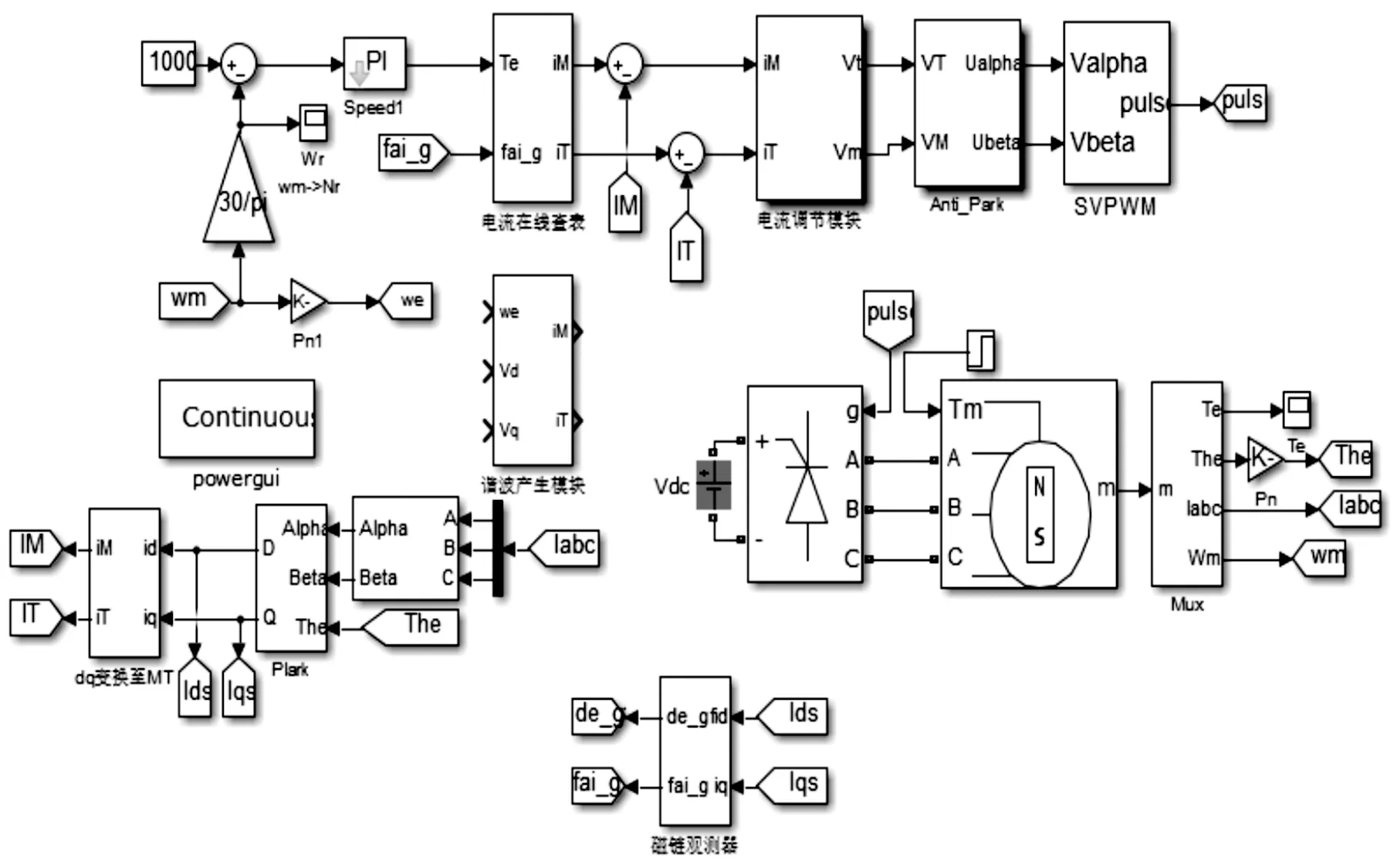
圖6 永磁同步電機氣隙磁場控制Simulink仿真模型示意圖

表3 仿真電機參數(shù)

圖6的Simulink仿真模型采用雙閉環(huán)控制，永磁同步電機、逆變器模塊選用電力系統(tǒng)庫(Sim Power Systems)工具箱內模型。經(jīng)坐標變換得到的id、iq輸入磁通估算模塊，輸出氣隙磁鏈幅值|ψg|和M軸與d軸角度δgf，其仿真模型結構如圖4所示。

電流在線查表模塊如圖7所示,在Matlab/Simulink中選擇二維查表模塊，將電機氣隙磁鏈幅值|ψg|，扭矩Te值分別與iM、iT值的關系輸入二維查表模塊，得到所需的電流值。

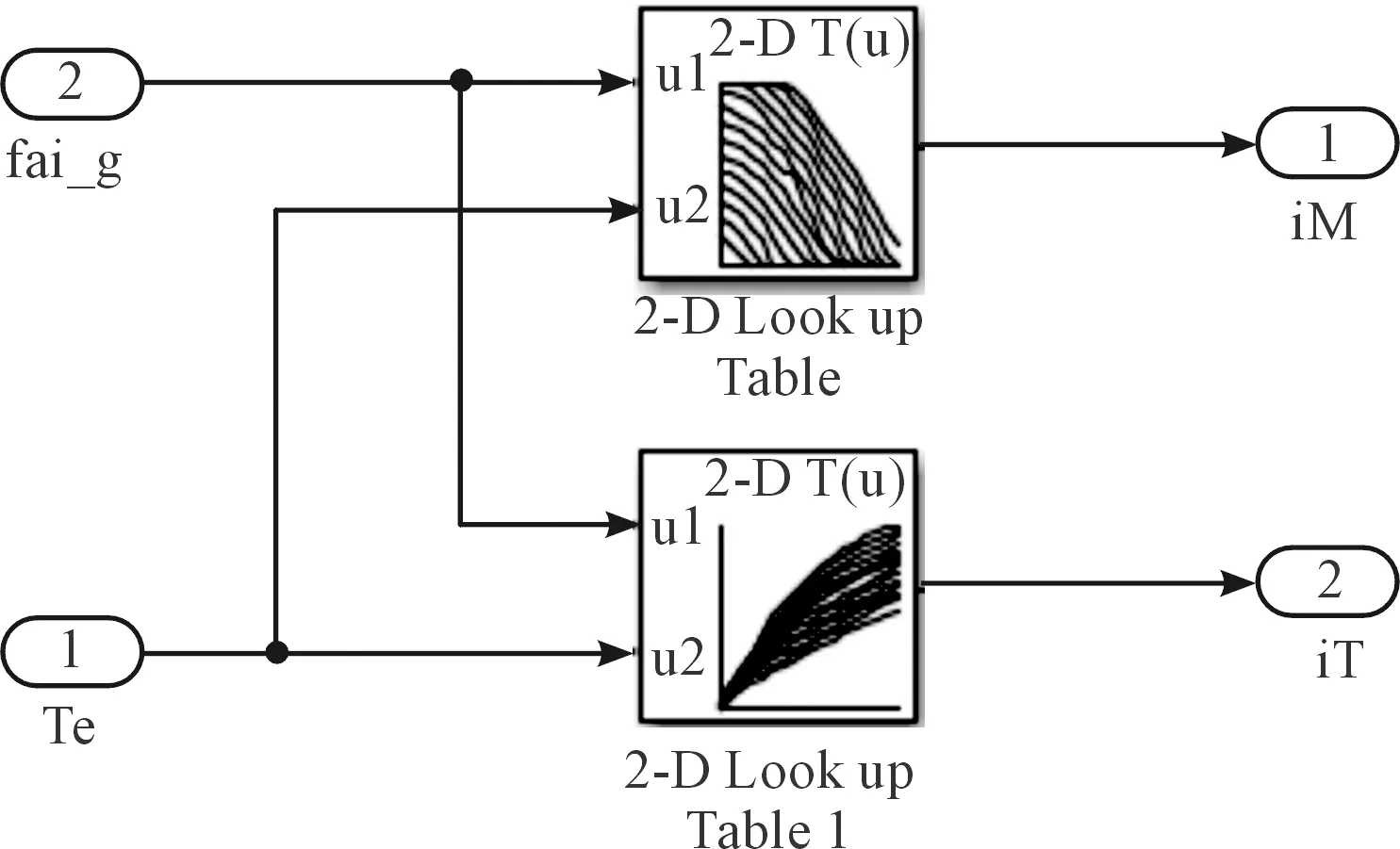
圖7 電流在線查表仿真模塊示意圖

為驗證控制永磁同步電機控制系統(tǒng)仿真模型的靜動態(tài)性能，電機空載啟動，額定轉速為1 000 r/min，在t=0.18 s時施加負載，在t=0.2 s時撤銷負載。得到系統(tǒng)電磁轉矩、轉速、電流仿真曲線如圖8～圖10所示。

根據(jù)仿真波形可得，在啟動階段存在較大的啟動轉矩和啟動電流，主要原因在于沒有對電流值進行限制。電機轉速在n=1 000 r/min的參考轉速下可實現(xiàn)快速動態(tài)響應，t=0.18 s時突增負載，電機轉速、轉矩有較大波動，穩(wěn)態(tài)運行時波形良好。 仿真結果表明：氣隙磁場定向可有效實現(xiàn)永磁同步電機動態(tài)穩(wěn)態(tài)控制。

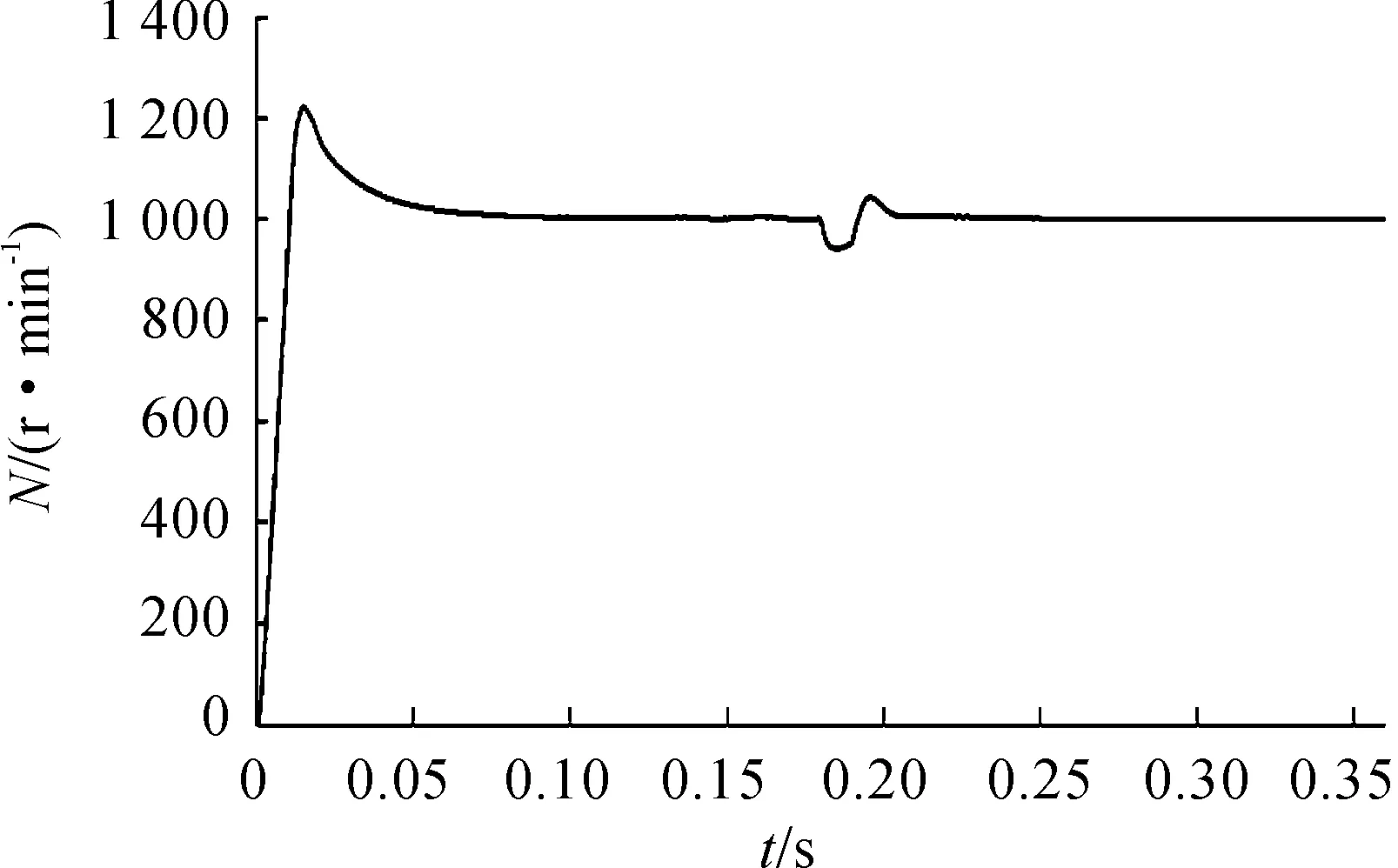
圖8 永磁同步電機轉速響應曲線

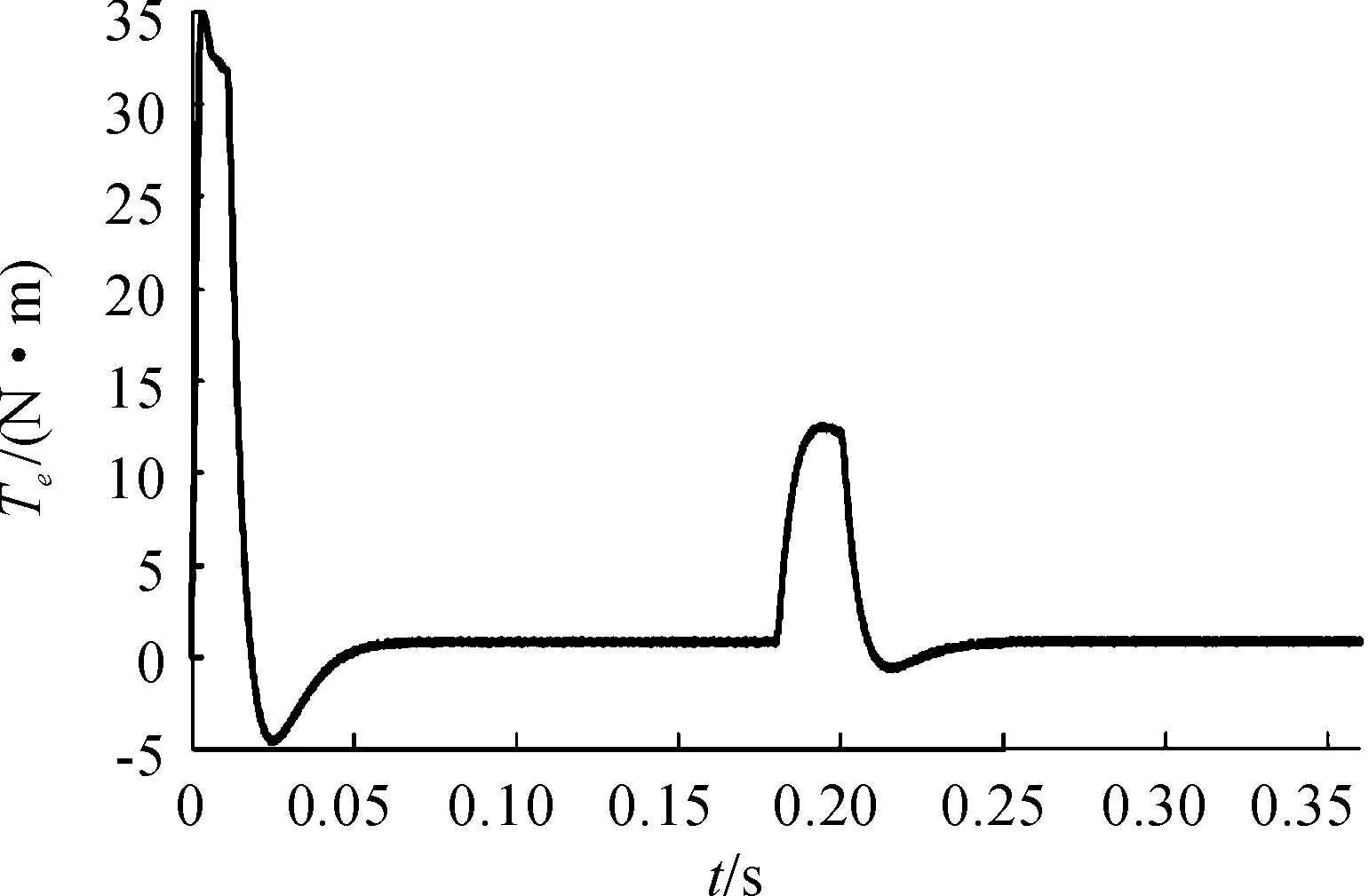
圖9 永磁同步電機電磁轉矩響應曲線

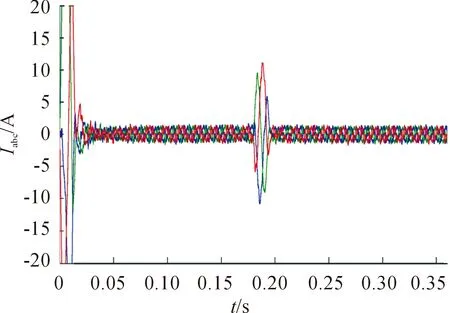
圖10 永磁同步電機電流響應曲線

為驗證永磁同步電機氣隙磁場定向控制在磁場諧波影響下的控制性能，建立諧波模型如圖11所示。

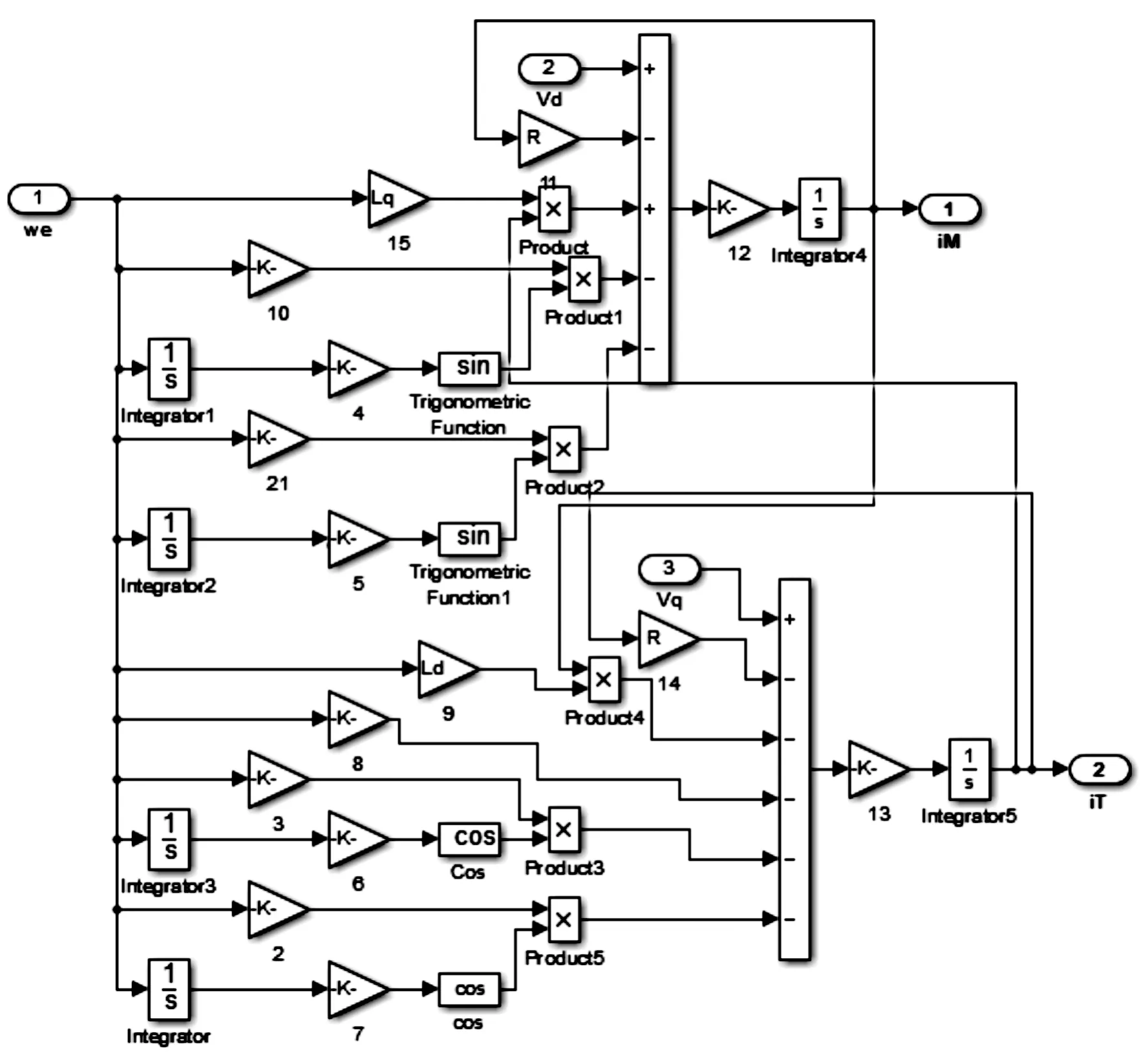
圖11 永磁同步電機諧波模型示意圖

使用諧波產(chǎn)生模型替換電流在線查表模塊，得到的氣隙磁場控制下的旋轉磁鏈與定子磁場控制下的旋轉磁鏈如圖12所示。

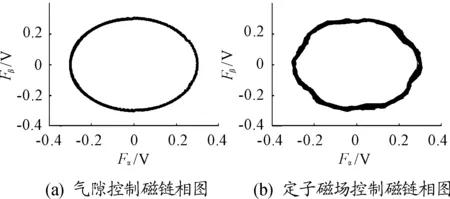
圖12 永磁同步電機磁鏈相圖變化曲線

由仿真曲線可得，定子磁場定向控制受高次諧波影響較大，磁鏈相圖軌跡出現(xiàn)許多凹凸不平，氣隙控制旋轉磁鏈受諧波影響較小，磁鏈相圖軌跡基本接近橢圓。

4 結論

本文在建立永磁同步電機數(shù)學模型的基礎上，提出了基于氣隙磁鏈定向的永磁同步電機仿真建模方法，在Matlab/Simulink中對該模型進行設計，仿真結果表明：波形符合理論分析，系統(tǒng)平穩(wěn)運行，具有較好的靜動態(tài)特性。采用該仿真模型，可以十分便捷地實現(xiàn)、驗證控制算法，為分析和設計控制系統(tǒng)提供了理論支持，也為實際電機控制系統(tǒng)的設計提供了思路。