基于RBF神經網絡增益調節的滑模制導律

佟廷帥,劉曉利,張志勇,何賢軍,陳志華

(1.南京理工大學 瞬態物理重點實驗室， 南京 210094;2.江蘇自動化研究所, 江蘇 連云港 222006)

隨著導彈等飛行技術的發展，傳統制導律已經不能滿足現代日益復雜的反導攔截要求[1-2]，新型導引律的研究和應用已成為導航領域的重點與熱門方向。

變結構控制系統對外界干擾和參數攝動具有良好的魯棒性[3]，為解決導彈制導問題提供了新的方向[4-7]。但變結構制導律需要根據目標機動性大小來調節變結構項增益，增益過大會導致角速率抖振，不利于彈上機構的正常工作，同時制導精度下降[8]；增益過小，則無法有效攔截目標。RBF神經網絡結構簡單，能夠逼近任意非線性函數，且學習收斂速度快,具有實現復雜環境下實時控制的能力，可被用來調節變結構項的增益。

本文將變結構控制理論與RBF神經網絡相結合，利用RBF神經網絡來自適應調節變結構項的增益。同時考慮控制回路對系統的影響，主要是自動駕駛儀的影響。仿真結果表明：基于RBF神經網絡增益調節的滑模制導律能有效削弱系統抖振，使脫靶量顯著減小，對變結構控制理論在導彈攔截中的應用具有重要指導意義。

1 三維空間攔截模型

為方便討論，首先建立三維空間攔截模型，如圖1所示。M和VM為導彈及其速度；T和VT為目標及其速度；Oxyz為地面坐標系；Ox2y2z2為彈道坐標系；Ox4y4z4為視線坐標系；θM,φM,θT,φT分別為導彈和目標的彈道傾角和彈道偏角；qε,qβ分別為視線傾角和視線偏角。

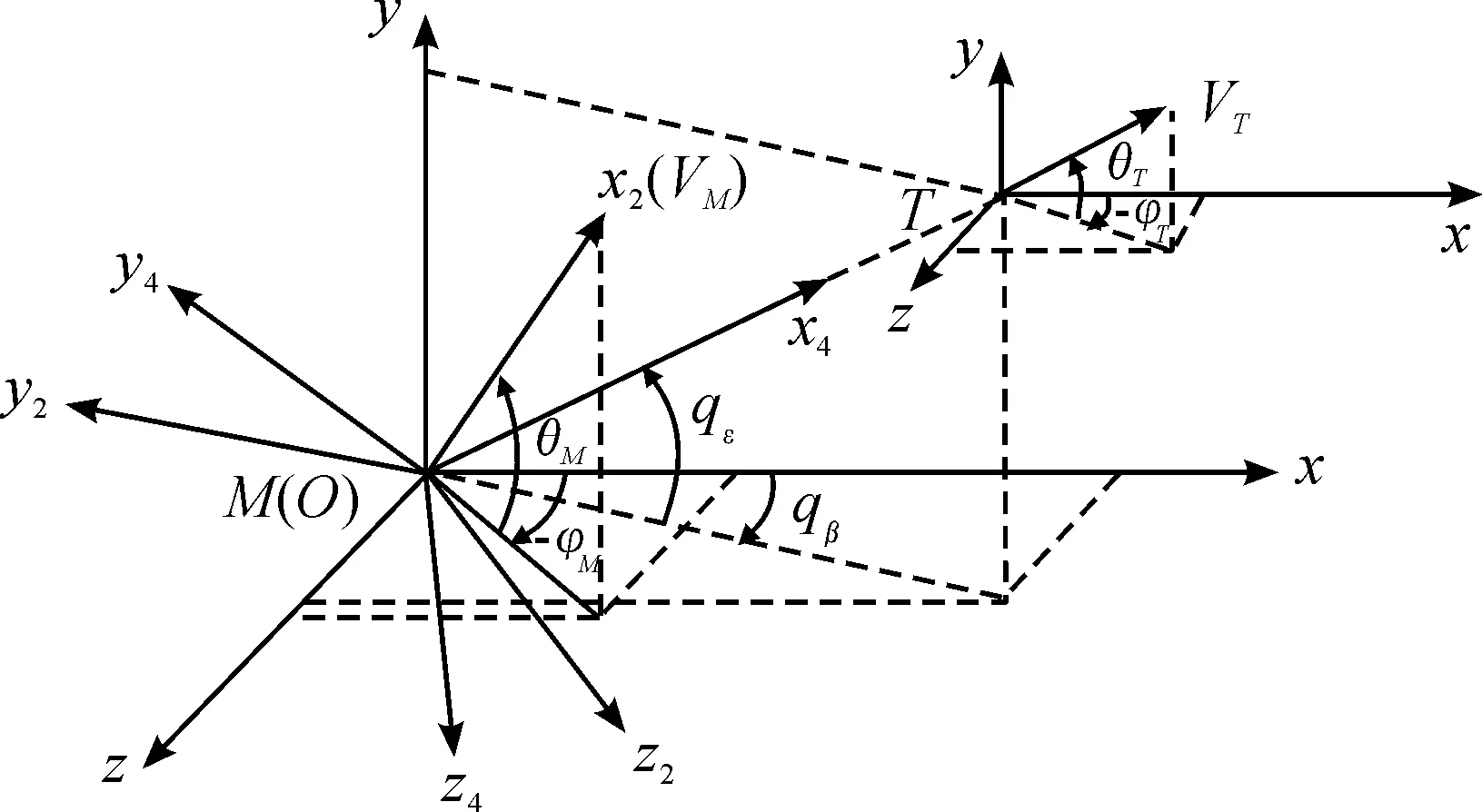
圖1 三維空間攔截模型示意圖

1.1 導彈的運動模型

在研究導彈運動特性中，把導彈運動分為質心運動和繞質心轉動。本文中，將導彈視為可操縱的質點，不考慮其繞質心的轉動，從而得到簡化后的導彈三自由度運動模型[9]：

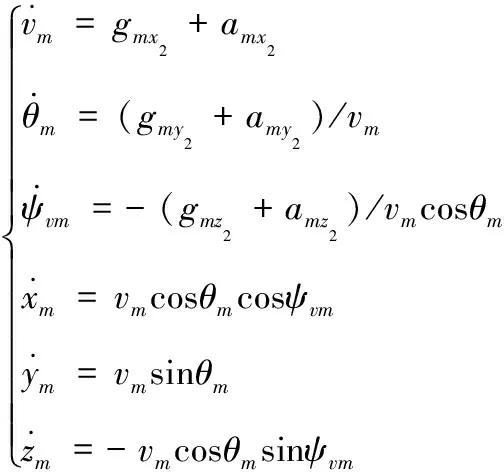
(1)

式(1)中：gmx2,gmy2,gmz2為重力加速度在彈道坐標系上的分量；amx2,amy2,amz2為導彈機動加速度在彈道坐標系上的分量；xm,ym,zm為導彈在地面坐標系中的位置。目標的運動模型和導彈類似。

1.2 導彈-目標相對運動模型

選取某一時間段Δt起始時刻的視線坐標系作為制導過程中導彈-目標相對運動的參考坐標系。在Δt內，此參考坐標系隨彈體平動。于是整個制導過程中的相對運動可以解耦成縱向平面和側向平面內的運動[10]。

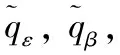
(2)

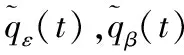
(3)

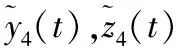
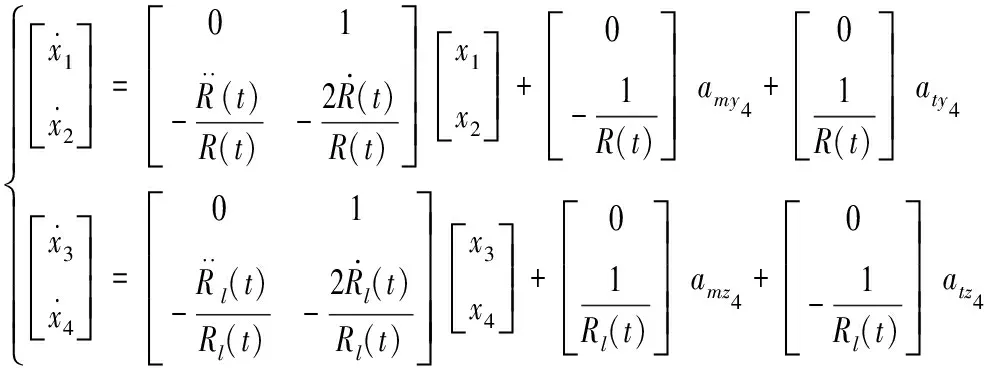
(4)

式(4)中：amy4(t),amz4(t),aty4(t),atz4(t)分別為導彈和目標機動加速度在Oy4和Oz4上的分量。

其中加速度指令由視線坐標系轉化到彈道坐標系在的轉換矩陣如下：

(5)

2 滑模變結構制導律

(6)

為了保證能夠良好地趨近滑模面，選取對導彈控制系統的時變性具有自適應能力的趨近律，即：

(7)

趨近律的物理意義在于當R較大時，趨近速率會適當放緩，當R→0時，趨近速率會迅速增加，避免視線角速率過早發散。當s→0時，趨近速率約為ε，可以保證在有限時間內到達滑模面。

將式(6)代入式(7)可得：

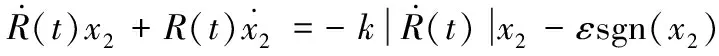
(8)

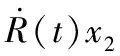
(9)

把式(3)代入式(9)，得到式(10)：

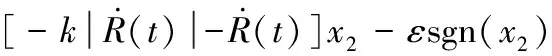
(10)

由于目標機動加速度無法準確獲得，可將其視為干擾量，可得：

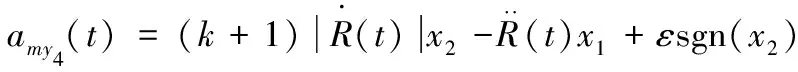
(11)

(12)

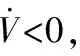
(13)

同理，側向平面的變結構制導律為：

(14)

3 基于RBF神經網絡的變結構項增益調節

由式(13)、式(14)可知，滑模變結構制導律是由比例導引項和變結構項組成。在導彈攔截目標時，目標機動和滑模制導律的變結構項均與視線角速率成正比。只有選取合適的ε，才能補償目標機動造成的視線角速率變化，否則會造成脫靶。

RBF神經網絡具有并行計算、分布式存儲、容錯能力強、快速學習、對任意非線性函數都具有良好的逼近能力、滿足復雜動態環境下非線性實時控制的特點。利用RBF神經網絡來自適應調節變結構項的增益，可達到削弱抖振和提高制導精度的目的，基于RBF神經網絡增益調節的滑模制導律攔截原理方框圖如圖2。將滑模面及其導數作為RBF神經網絡輸入，輸出作為變結構項增益。

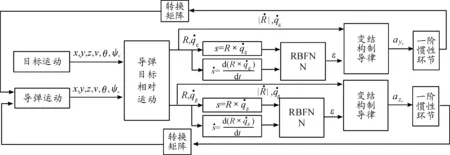
圖2 基于RBFNN增益調節的滑模制導律攔截原理方框圖

RBF神經網絡的網絡結構如下：

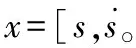
隱含層：隱含層中神經元的激活函數即徑向基函數是對中心點徑向對稱且衰減的非負非線性函數。對輸入信息進行空間映射的變換，這里激活函數取高斯函數：

(15)

式(15)中，ci和bi分別是隱含層第i個神經元的中心點和基寬度。||·||表示歐式范數。

輸出層：對輸入模式進行響應。輸出層神經元的作用函數為線性函數，對隱含層神經元輸出進行線性加權后輸出，作為整個神經網絡的輸出結果。本文中神經網絡輸出為變結構項增益ε=|WTh(x)|，其中W為網絡權值向量。

RBF神經網絡學習算法如下：

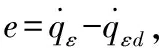
輸出層權重，隱含層單元中心及基寬度參數調整算法如下：

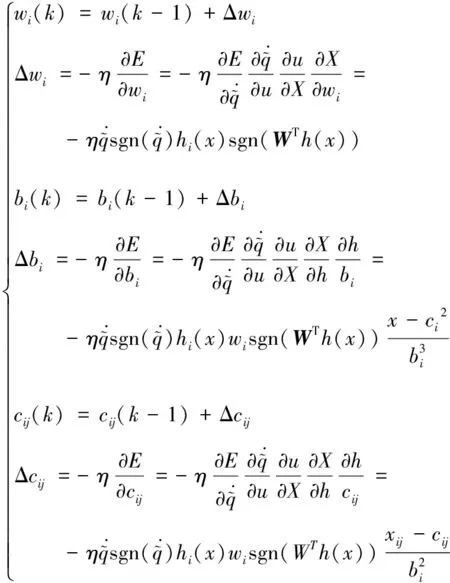
(16)

式中η∈(0,1)為學習速率。

4 仿真結果及分析

為了驗證基于RBF神經網絡增益調節的滑模制導律的有效性，利用Matlab進行仿真。初始仿真參數見表1。

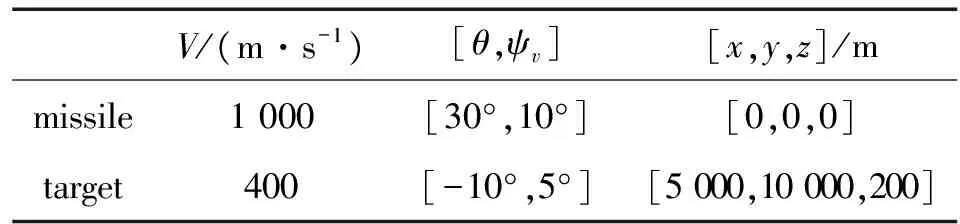
表1 導彈-目標的初始仿真參數

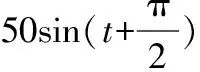
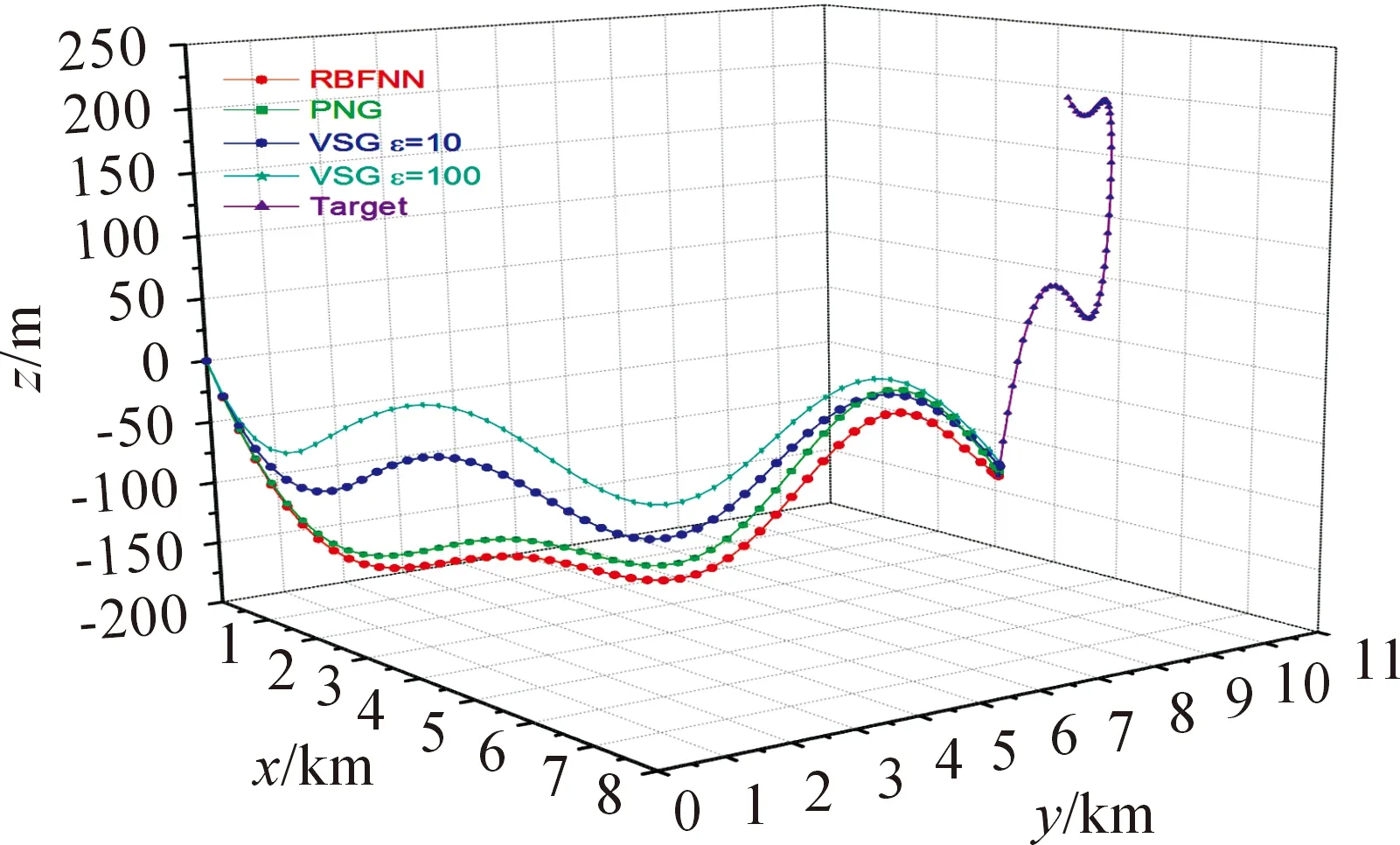
圖3 aty2=-7g時導彈-目標運動軌跡

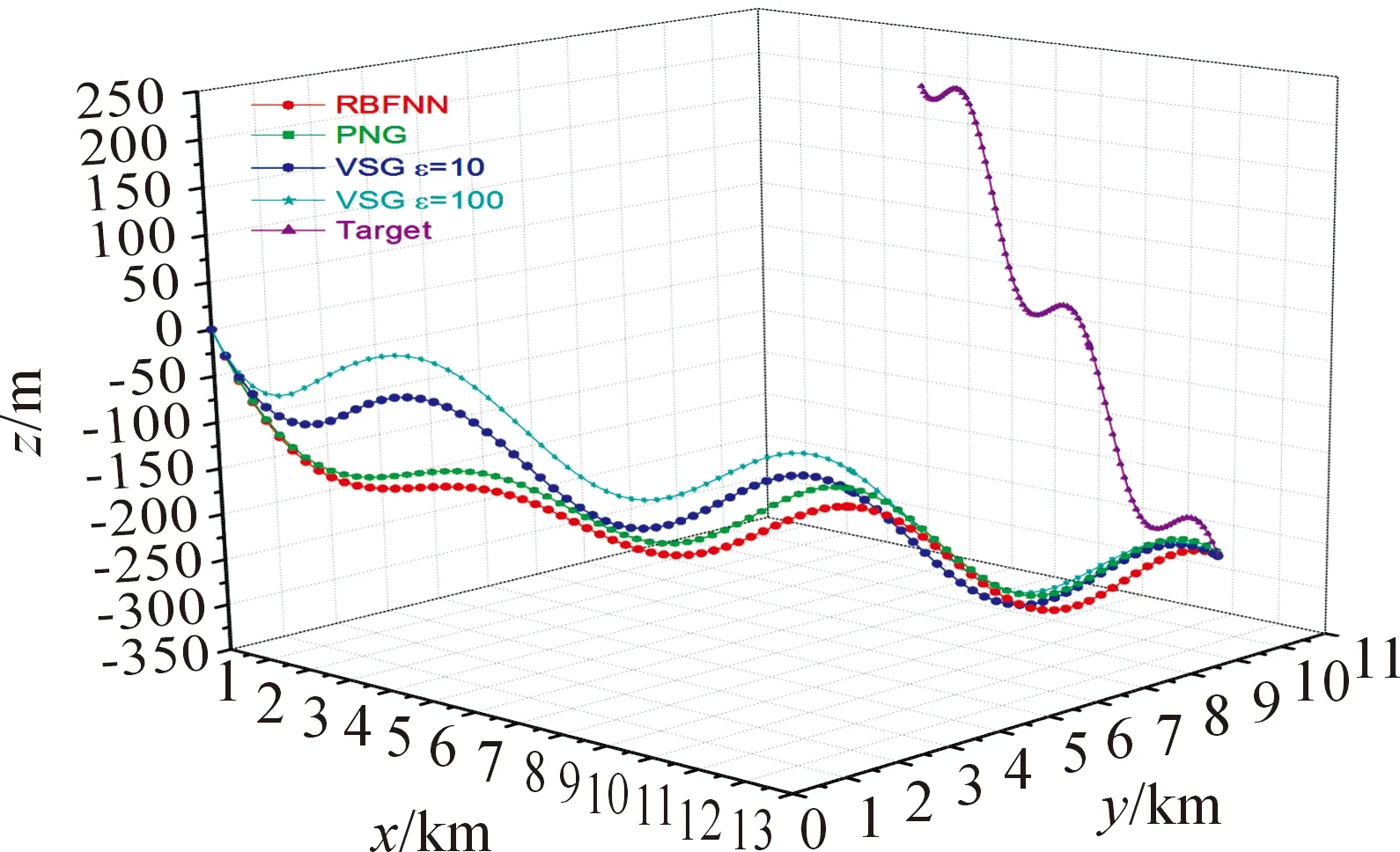
圖4 aty2=2g時導彈-目標運動軌跡

圖5 aty2=-7g時的視線角速率變化

圖6 aty2=2g時的視線角速率變化

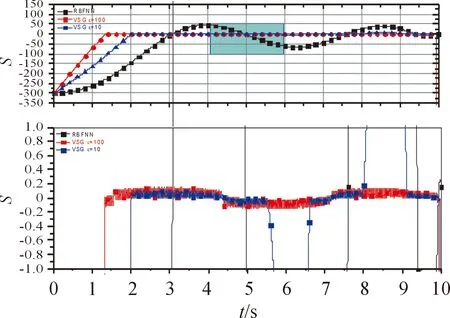
圖7 aty2=-7g時S的變化

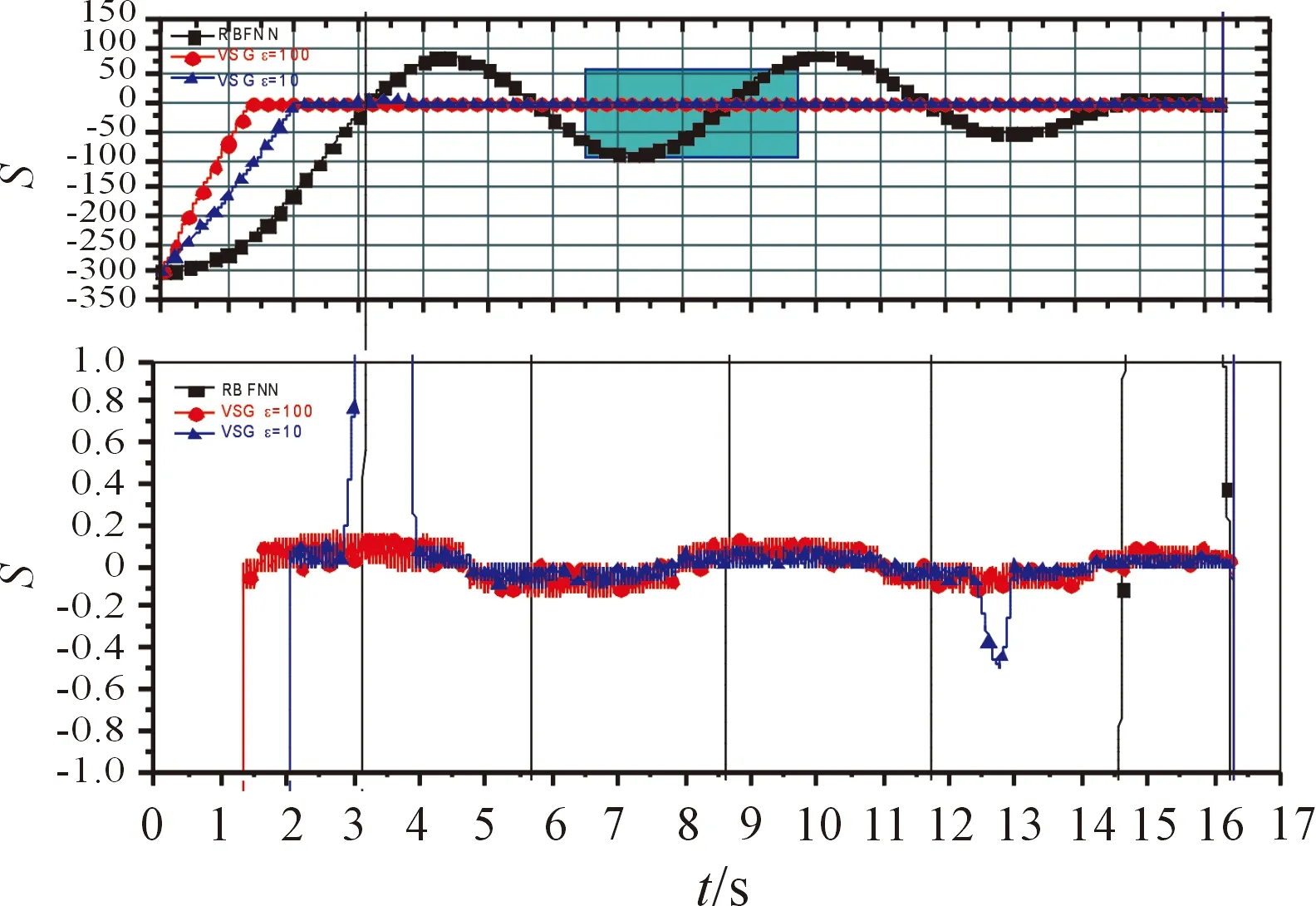
圖8 aty2=2g時S的變化

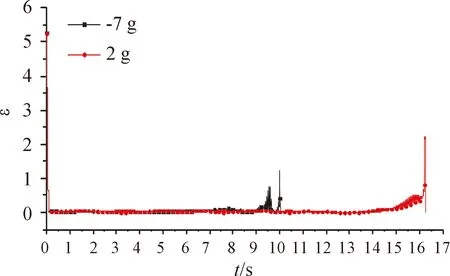
圖9 aty2=-7g；2g時ε的變化

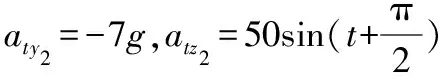
5 結論

1) 針對傳統導引法無法有效攔截高速、大機動目標以及忽略自動駕駛儀動態特性等問題，結合變結構控制理論和神經網絡，提出基于RBF神經網絡增益調節的滑模制導律,利用RBF神經網絡自適應調節變結構項增益。

2) 與比例導引法和固定增益滑模制導律相比，基于RBF神經網絡增益調節的滑模制導律脫靶量有顯著減小；同時，與固定增益滑模制導律相比，基于RBF神經網絡增益調節的滑模制導律能有效削弱系統的抖振，對于目標的機動具有較強的魯棒性。