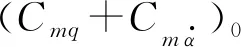返回艙跨聲速自由飛行的靜動穩定性

宋 威, 艾邦成, 蔣增輝, 魯 偉

(中國航天空氣動力技術研究院, 北京 100074)

0 引 言

在再入大氣層的過程中，返回艙要經歷高超聲速、低亞聲速等較寬的馬赫數范圍，經歷稀薄流、滑移區、連續流，并伴隨有熱力學和化學非平衡流的繞流環境，形成特征差異極大的流動狀態，從而極大地影

響返回艙整體空氣動力學特性[1]。考慮到防熱、減阻及具有一定升阻比等要求，返回艙通常采用大鈍頭球冠倒錐外形，且一般設計為靜穩定的。但它與常規大升阻比、細長體飛行器的動穩定特性顯著不同，一般在馬赫數Ma=0.8～1.4范圍內動不穩定[2- 3]，其動態穩定性是設計中尤其需要注意的問題。

針對返回艙的動態穩定性問題，國內外開展過大量的數值模擬[4- 10]，但這些理論計算很難計及鈍頭氣流分離、后體氣流再附、船尾近尾流和動態時滯等效應的影響，在跨聲速區對具有較大分離效應的球冠倒錐形返回艙氣動阻尼系數計算會造成較大誤差。因此，對此類大鈍頭返回艙的動態穩定性，目前主要依靠地面風洞試驗確定[11- 14]。如宋玉輝[11]采用風洞自由振動試驗方法研究發現，返回艙動穩定導數系數的量級在全馬赫數范圍內都很小，在高亞聲速和跨聲速范圍有正號的俯仰阻尼導數出現。Mitcheltree[13]在亞聲速風洞中研究不同前體外形的返回艙動穩定特性，試驗結果顯示頭部鈍度與半錐角的變化對返回艙的動態穩定性影響不大，但質心位置直接影響返回艙的動態穩定性。

上述以風洞動態試驗研究返回艙動態穩定性的特點是：模型采用尾部支桿固定(運動自由度受到嚴重約束)，存在一定的支桿干擾，模型尾部會產生分離流動形成回流，尾部迎風面與背風面形成附加后體力，加大試驗支撐的干擾，有可能改變模型阻尼性質[14]，導致試驗數據不真實。因此，國內外另行考慮采用自由飛試驗技術來研究返回艙的動態穩定性。從文獻來看，此類研究工作主要集中于彈道靶自由飛試驗[15- 19]。如Chapman[15]通過彈道靶試驗研究Stardust返回艙外形的靜、動氣動力特性，試驗中都出現了動不穩定的極限環現象，Chapman通過分析認為，俯仰阻尼系數的高度非線性是造成返回艙動不穩定的主要原因。Cheatwood[19]通過彈道靶自由飛試驗研究發現，Genesis返回艙外形的動穩定性隨著馬赫數的減小而急劇惡化，在Ma=2.5左右，其極限環振幅就達到65°。而采用風洞模型自由飛試驗技術研究大鈍頭、小升阻比返回艙動態穩定性的工作，基本未見文獻發表。因此，本文開展大鈍頭返回艙跨聲速風洞自由飛試驗，主要考察返回艙的動態穩定性問題；由于采用線性與非線性氣動參數辨識時，可以得到飛行器靜態穩定性導數系數，因而同時給出返回艙靜穩定導數系數的變化規律。

1 試驗方案

1.1 試驗方法

本次返回艙跨聲速自由飛行的動態穩定性試驗采用發射式風洞自由飛試驗方法。試驗模型以夾持器抱緊并安置在帶有氣動推桿的發射槍內，整套發射槍與風洞刀架相連，可通過改變刀架的迎角改變模型的初始發射迎角α。當風洞起動且氣流穩定后，同步控制儀發出信號，高壓氣源開始供氣，推動試驗模型以一定的速度vx(遠遠小于來流風速v)發射到穩定流場中。模型在風洞均勻穩定流場中無約束“自由飛行”近200mm，能夠盡量減少發射帶來的初擾動。當模型進入觀察窗時，布置在觀察窗附近的數字式高速攝像機啟動，拍攝并存儲風洞流場中的模型動態運動圖像。模型發射速度可通過調節活塞發射壓力以及活塞行程進行控制。

1.2 風洞自由飛試驗研究飛行器動態穩定性所需滿足的相似律

風洞自由飛試驗具有獨特的優勢，在飛行器動態穩定性研究中得到越來越廣泛的應用，其中一項關鍵技術是試驗模型相似設計[20]。作為一種地面風洞試驗手段，風洞自由飛試驗模型設計首先要考慮模型與飛行器所需滿足的相似律，與其他所有風洞試驗模型一樣，需要遵循相關的氣動相似準則(幾何相似、馬赫數相似、雷諾數相似等)；另外，風洞自由飛試驗的特點是模型的運動自由度不受支桿約束，因此還需保證運動動力學相似。在獲取表征飛行器動態穩定特性的動穩定導數系數試驗中，全尺寸飛行器與風洞試驗模型之間的運動動力學相似是通過減縮頻率k這一參數實現的：

k=(ωd/v)M=(ωd/v)S

(1)

更重要的一點，是在高速攝影拍攝區內取得足夠的自由飛行運動信息。本次試驗在獲取動穩定導數系數時，需取得運動振動周期數T，這是保證試驗精度的關鍵點。模型的振動周期數可用式(2)估算[21]：

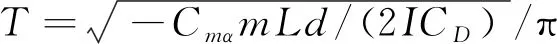
(2)

式中，CD為試驗條件下有效阻力系數，L為模型飛越觀察窗的距離，m為模型的質量。

1.3 試驗設備及模型

試驗在中國兵器工業總公司第203所CG01風洞中進行。CG01風洞是跨超聲速、暫沖式風洞，以空氣為工作介質，試驗段截面尺寸為600mm×600mm，側壁觀測窗尺寸為700mm×250mm。

采用單臺高速攝像機進行單平面流場背光拍攝(光線方向與攝像機鏡頭指向相反)。光路系統如圖1所示，攝像機布置于觀察窗側面，能夠記錄試驗模型沿縱向、鉛垂方向以及俯仰方向的運動。試驗馬赫數0.8，高速攝像機拍攝速度2 000幀/s，相鄰2幀圖像的時間間隔t=0.5ms。圖2為返回艙試驗模型外形圖(xg、yg分別為模型質心的橫、縱坐標，質心位置如圖2(b)所示)。返回艙模型的流場參數及質量特性參數如表1所示。

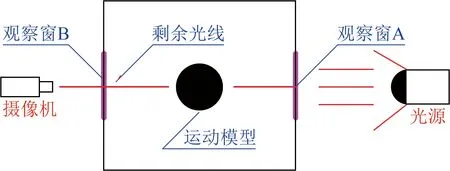
圖1 光路系統示意圖

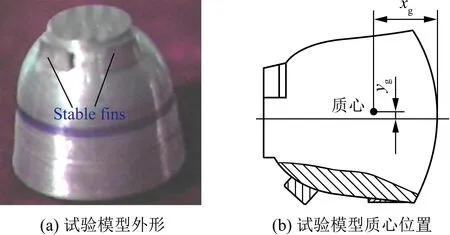
圖2 返回艙模型外形圖

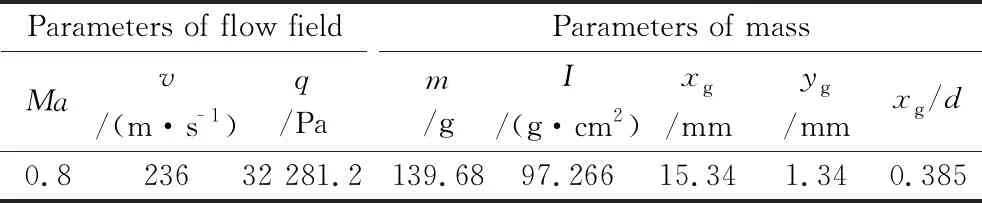
Parameters of flow fieldMav/(m·s-1)q/PaParameters of massm/gI/(g·cm2)xg/mmyg/mmxg/d0.823632 281.2139.6897.26615.341.340.385

2 試驗數據處理

風洞自由飛試驗記錄的是模型相對于風洞固定坐標系的姿態角，有θ=γ+α，其中θ為模型相對于慣性坐標系的俯仰角，γ為航跡角，α為模型飛行迎角。航跡角計算如下：

(3)

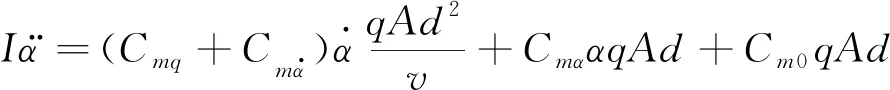
(4)

非線性氣動參數辨識采用如下單自由度俯仰振蕩運動方程[22](假設俯仰靜穩定導數系數和動穩定導數系數隨迎角呈二次曲線變化)：

+(Cmα0+Cmα2α2)αqAd

(5)

此時靜穩定導數系數和動穩定導數系數分別為：

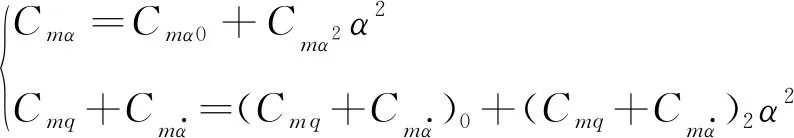
(6)

采用參數微分法[23](Chapman- Kirk方法，簡稱“C- K方法”)，從表征單自由度俯仰運動的微分方程入手，直接辨識出其中的靜動穩定性參數。辨識精度由擬合精度SD(α)給出[24]：

(7)

式中，Ν為辨識過程中待定系數的個數，n為參與辨識的數據點數。

3 試驗結果與分析

3.1 返回艙自由飛行運動圖像序列

圖3為Ma=0.8、初始發射迎角α=0°、初始側滑角β=0°試驗狀態下，由高速攝像機通過風洞觀察窗拍攝的返回艙模型在豎直平面內(近似為模型的迎角α平面)逆來流方向自由飛行的動態運動圖像序列(由于拍攝速度較高，每間隔16幀圖像取1幀)。由圖3可定性獲得三點運動信息：(1)返回艙模型在自由飛行運動的過程中俯仰方向出現明顯的振蕩運動(圖中不易分辨出振幅是衰減還是增加的，需通過圖像自動判讀出俯仰角θ的時間歷程方可知曉)；(2)返回艙模型縱向運動時(平行于氣流，定義為x方向)，從觀察窗一側“飛入”，自由飛行到另一側時絕對速度恰好為零，然后“倒飛”回來，這可以通過設置合理的初始發射壓力參數來實現，目的是獲得更多的試驗記錄畫面；(3)在垂直方向(垂直于氣流，定義為y方向)，返回艙模型在氣動升力與重力的共同作用下逐漸下降。

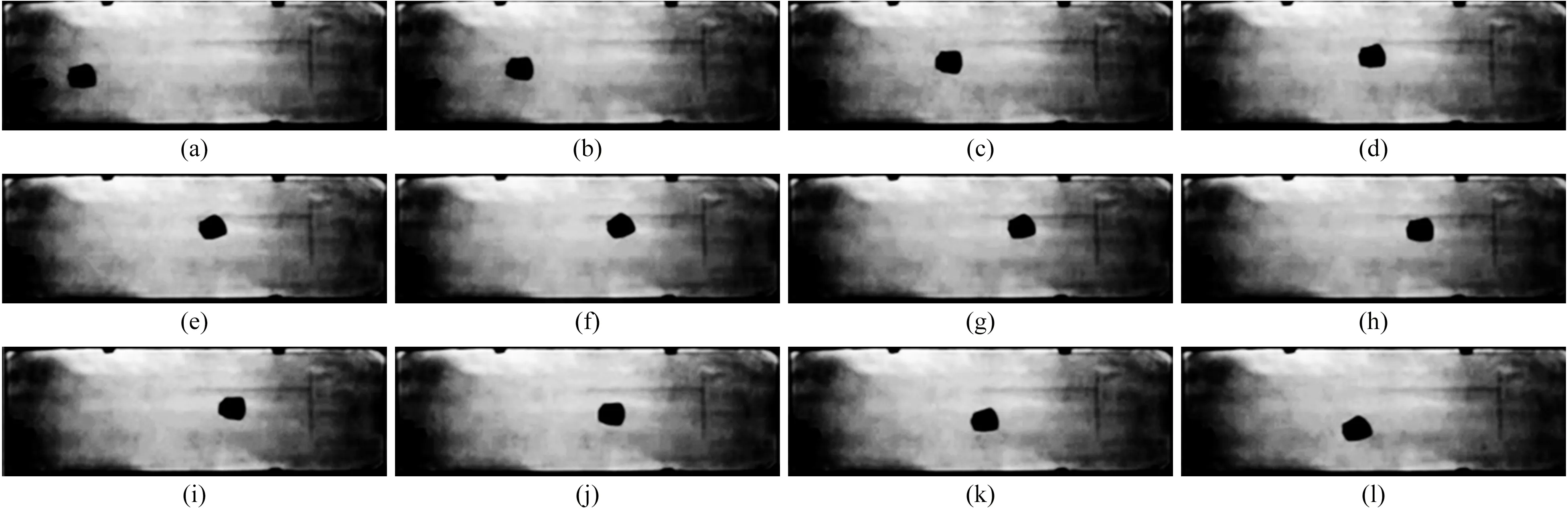
圖3 返回艙模型在風洞中自由飛行序列圖像

3.2 返回艙自由飛行的姿態角及運動軌跡

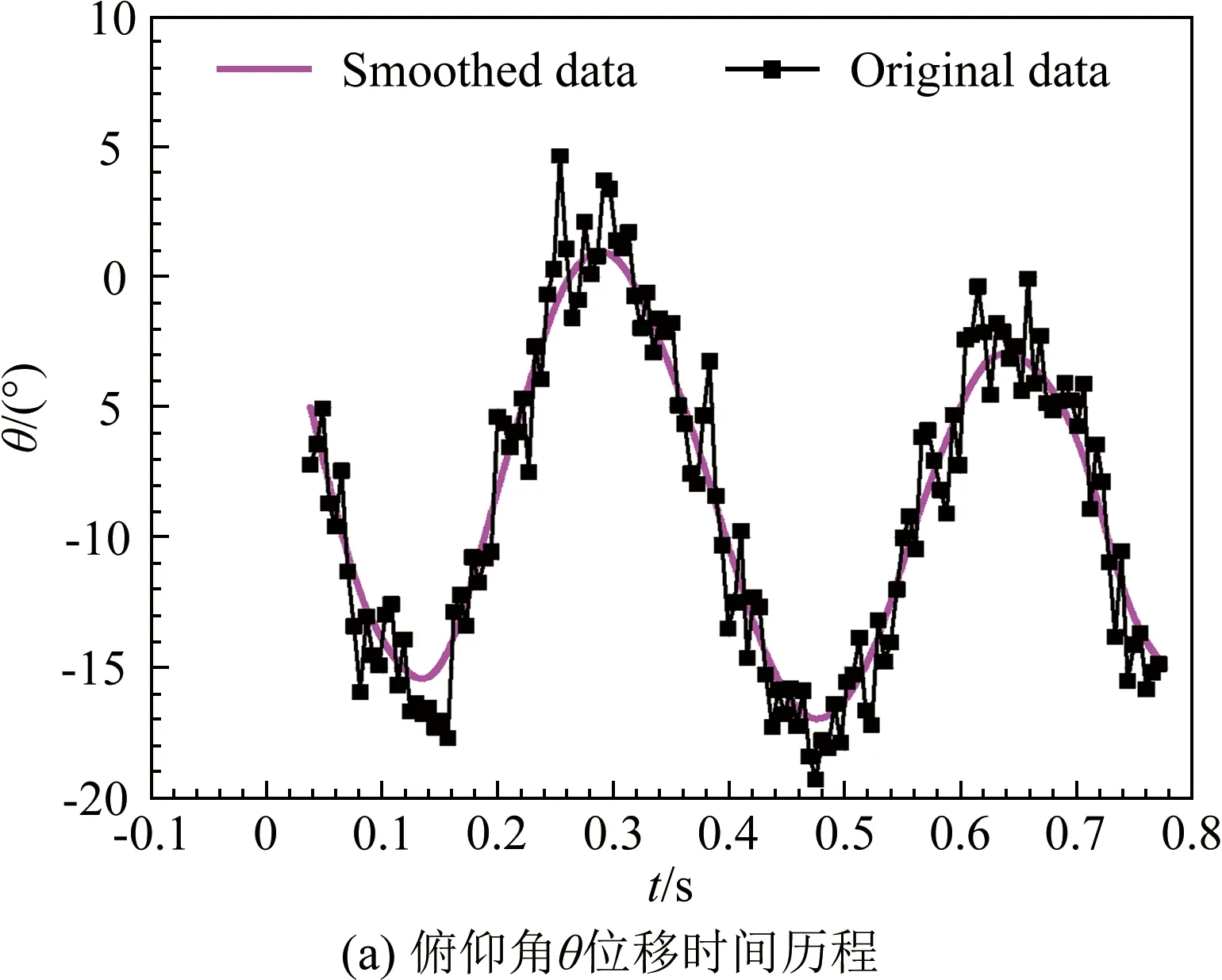
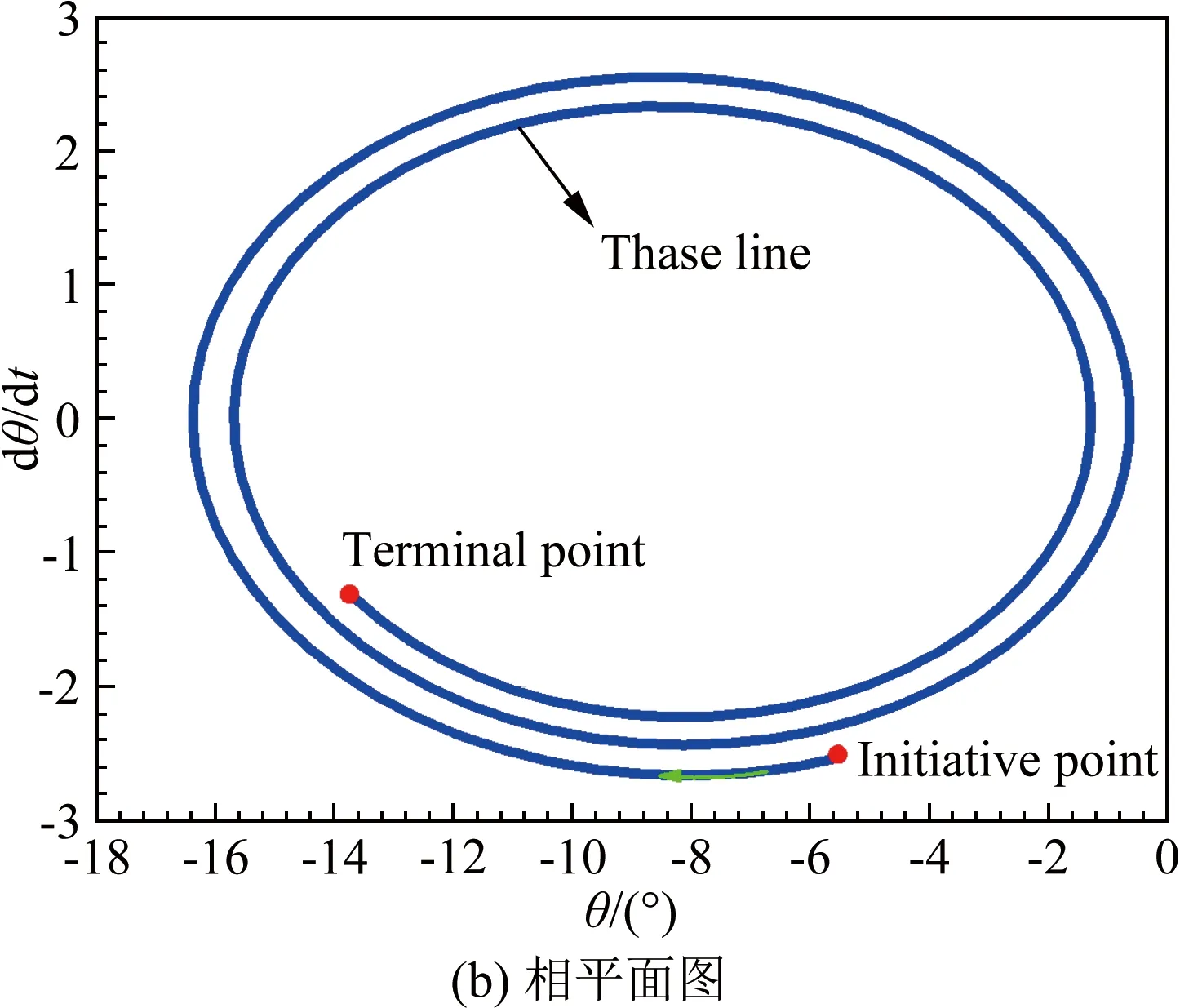
圖4 返回艙模型俯仰角位移時間歷程及相平面圖

Fig.4Historyofpitchangleandphase-planediagramofthere-entrycapsule

圖5 返回艙線位移時間歷程圖

3.3 返回艙的靜、動態穩定特性

圖6為Ma=0.8、初始發射迎角α=0°、初始側滑角β=0°試驗狀態下，返回艙模型迎角α測量值與辨識回代值對比圖。將線性氣動參數辨識所得的氣動參數代入運動方程(1)，復現的俯仰角位移時間歷程與原始數據點在大迎角范圍內有所偏離，在小迎角范圍內重合度較好；將非線性氣動參數辨識所得的氣動參數代入運動方程(2)的回代值，與原始數據點的重合度較好。

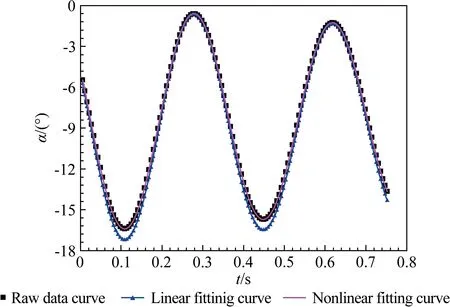
圖6 迎角測量值與辨識回代值對比圖

Fig.6Comparisonofmeasurementandbacksubstitutionofangleofattack

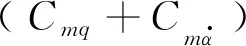
表2 線性與非線性氣動參數辨識結果對比表Table 2 Comparison of nonlinear and linear aerodynamic parameter identification

圖7為采用非線性氣動參數辨識所獲得的靜穩定導數系數線性項、非線性項及總靜穩定導數系數隨迎角變化曲線(迎角α范圍為-16.376°～0.976 09°)。由圖7可以看出：返回艙靜穩定導數系數的數值主要由線性項Cmα0決定，非線性項Cmα2α2所占比例較小；總靜穩定導數系數Cmα與線性項Cmα0在大迎角附近有一定差距，在小迎角附近幾乎重合，這也表明類“聯盟號”返回艙靜穩定導數系數的非線性較弱，可近似用線性模式來獲取。

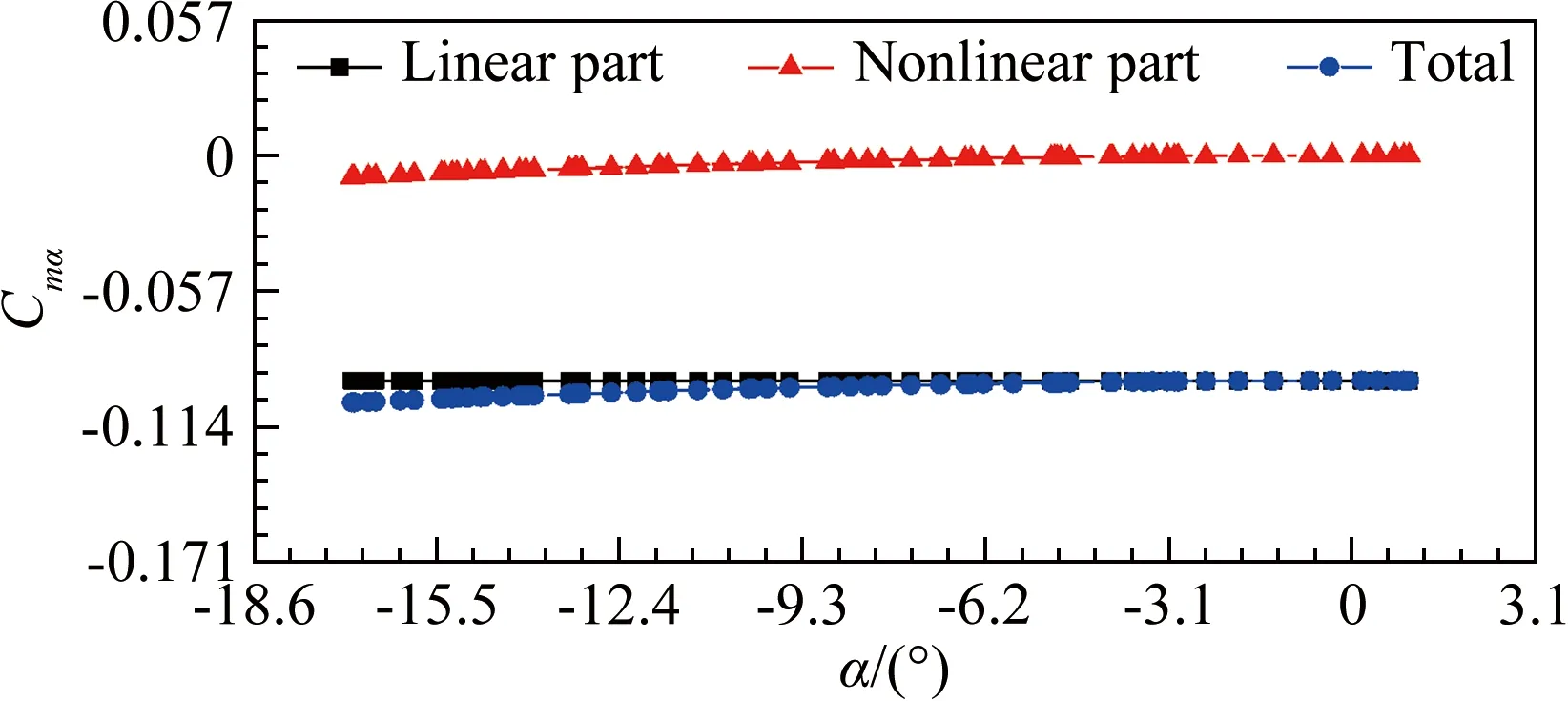
圖7 非線性參數辨識的線性項、非線性項及總靜穩定導數系數隨迎角α變化曲線

Fig.7Thelinear,nonlineartermandtotalstaticderivativecoefficientcurvesvarywithangleofattackαfornonlinearparameteridentification

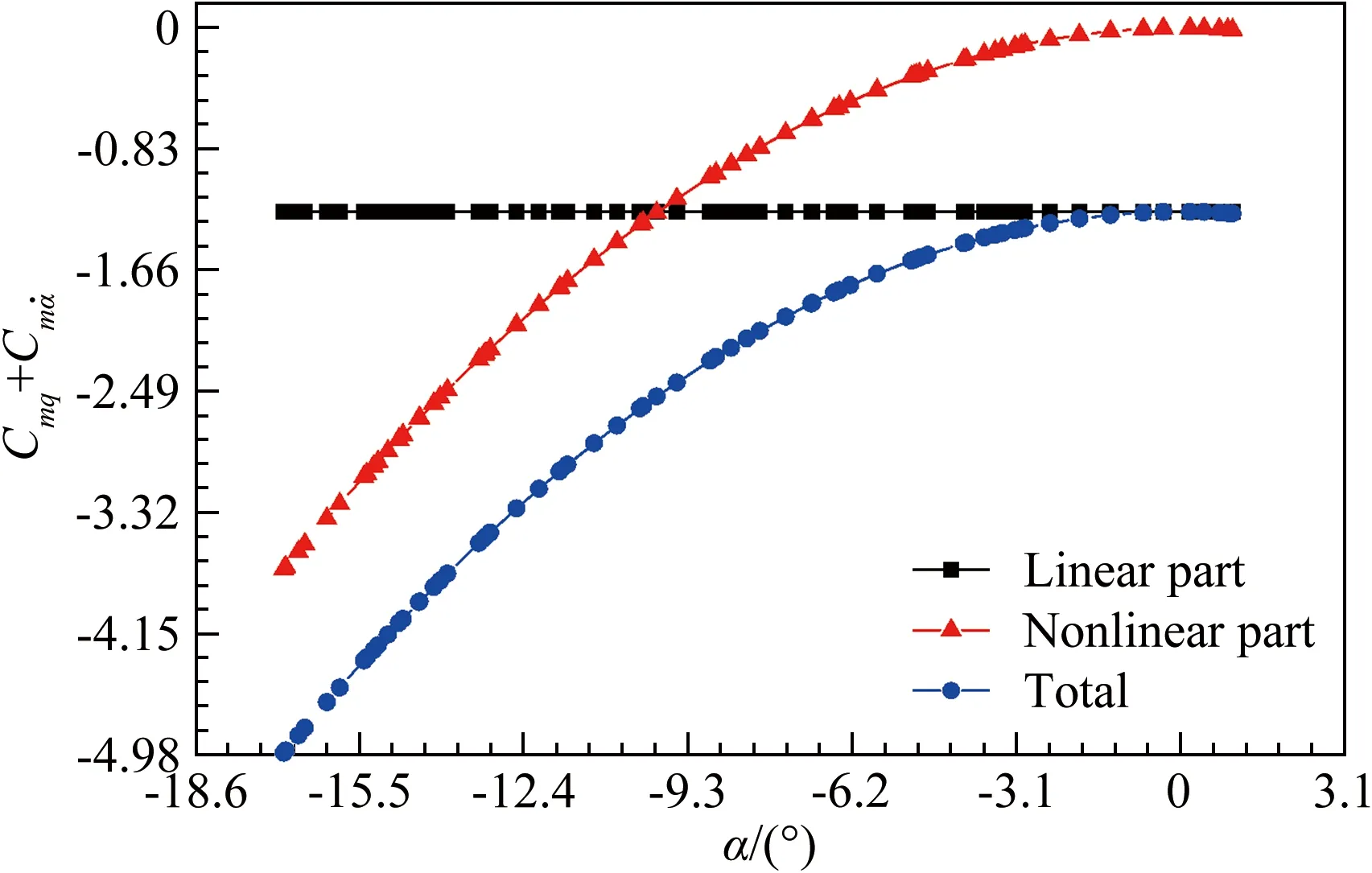
圖8 非線性參數辨識的線性項、非線性項及總動穩定導數系數隨迎角α變化曲線

Fig.8Thelinear,nonlineartermandtotaldynamicderivativecoefficientcurvesvarywithangleofattackαfornonlinearparameteridentification

4 結 論

采用風洞自由飛試驗技術研究大鈍頭、小升阻比的類“聯盟號”返回艙自由飛行運動特性與氣動特性規律，研究結果表明：

(1) 采用線性與非線性氣動參數辨識所獲得的靜穩定導數系數Cmα均小于0，在數值上差距不大。從非線性氣動參數辨識結果看，返回艙靜穩定導數系數的數值主要由線性項Cmα0決定，非線性項Cmα2α2所占比例較小，總靜穩定導數系數Cmα與線性項Cmα0在大迎角附近有一定差距，在小迎角附近幾乎重合，類“聯盟號”返回艙靜穩定導數系數的非線性較弱，可近似用線性模式的氣動參數辨識來獲取。