粒子運動軌跡的圖像處理及流場重構算法研究

吳 凡, 周 騖, 蔡小舒

(上海理工大學 顆粒與兩相流測量研究所,上海 200093)

0 引 言

流動廣泛存在于化工和能源等行業，復雜流動現象中流動參數的獲取通常十分重要[1- 2]。 目前有很多測量顆粒速度的方法，其中非侵入式的光學測量按照原理有兩大類，即基于多普勒原理的測量方法和基于TOF(Time of Flight)的測量方法[3]。 前者利用激光照射顆粒產生的多普勒頻移測速，后者則根據單位時間內顆粒移動的距離來計算速度[4]。

典型的基于TOF的測量方法包括PIV(Particle Image Velocimetry)和PTV(Particle Tracking Veloci- metry)。PIV是20世紀70年代末發展起來的一種非接觸式流體力學測速方法，是目前應用最為廣泛的全場無干擾測速手段[5]。PTV技術本質上是PIV技術的衍生，兩者的不同之處在于:PIV獲取的速度來自于觀測區域內多個粒子位移的統計平均值，而PTV則是通過追蹤單個粒子的位移來獲得速度。PTV由于其追蹤顆粒運動的特點，所得結果具有直觀性和準確性，不過同時也具有粒子濃度不宜過高的局限性[6]。早期PTV技術由于CCD攝像系統水平的

限制，其時間和空間分辨率均不高，精度也不如PIV[7]。隨著計算機和CCD相機等硬件水平的不斷提高，在輸移現象和傳送現象等尤其關注顆粒的拉格朗日運動過程的情況下，PTV的作用逐漸顯現出來，因而也得到了廣泛的應用[8]。

根據圖像記錄的方式不同，PTV可以分為3種類型：單幀單脈沖、單幀多脈沖和多幀單脈沖[9]。近年來PTV領域的研究大多集中在多幀單脈沖形式[10]。多幀單脈沖形式具有更高的精度且能很好地解決速度二義性問題，因而得到廣泛應用。不過當涉及湍流這種十分復雜、瞬息萬變的流動時， 通常需要頻率非常高的激光脈沖， 才能實現對復雜流動顆粒的精確追蹤， 但同時也會造成成本的急劇增加。

單幀單曝光圖像法，即PTV的單幀單脈沖形式，具有系統簡潔、圖像直觀等優點。由于只有一次曝光，因此不需要功率非常大的激光器即可完成對示蹤粒子的追蹤。不過單幀單曝光圖像法的圖像處理過程相對復雜，不同于多幀單脈沖形式的PTV，單幀單曝光雖然沒有粒子匹配的問題，但由于其處理對象是軌跡而非單個點，復雜度也有所提升。

近年來對PTV的研究多集中在多幀單脈沖形式，對單幀單曝光圖像法的處理算法研究相對較少。其中，劉春嶸等[11]通過形心主軸的概念來計算運動軌跡的速度； 陳晶麗等[12]提出針對顆粒運動軌跡采用外接矩形的方法來提取顆粒速度與粒度；Jing等[13]則提出了通過檢測軌跡邊緣8個特征點來計算速度與粒度的方法。上述3種方法各有優勢和特點，不過三者有一個共同點，那就是針對一條軌跡處理出一個速度矢量，導致信息的利用率較低。同時，在處理彎曲軌跡時，這些方法的精度均有所下降，而復雜流場中的彎曲軌跡是無法避免的。因此，本文提出一種方法，不僅能同時提取直線段軌跡和彎曲段軌跡的速度矢量，同時也提高軌跡上運動信息的利用率。

1 單幀單曝光圖像法測速原理

在利用單幀單曝光圖像法測量示蹤粒子的速度時，一般CCD相機固定不動，通過視窗記錄測量區的圖像，此時，離散相顆粒(如水滴、煤粉、氣泡等)與CCD相機發生相對位移， 其成像在曝光時間內的疊加就形成了模糊的“拖影”，如圖1所示[14]。

單幀單曝光運動模糊圖像包含了顆粒與相機的相對位移信息。因為曝光時間已知，在物體勻速直線運動假設的前提下，可以計算出運動速度，如式(1)所示。

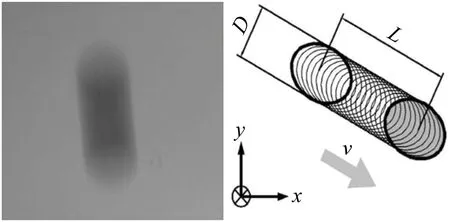
圖1 運動模糊圖像及其成像模型

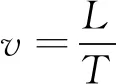
(1)

式中，T為曝光時間且已知，故速度v的計算關鍵就在于運動長度L的計算。現有的很多算法都將軌跡近似視為一段直線，且最終得出一個速度矢量。以外接矩形法為例，該方法求出軌跡的最小外接矩形，提取矩形的長和寬，長度減去寬度便得到了顆粒的運動距離。其他幾種算法各有不同，但都具有一定的相似性。上述算法均需滿足顆粒運動軌跡接近直線的前提，在顆粒軌跡為曲線的情況下會產生一定誤差。所以需要提出另一種計算速度的方法，能同時適用于直線軌跡和彎曲軌跡的情況。

2 基于骨架提取的顆粒軌跡處理算法

骨架提取，也被稱為二值圖像細化。這種算法能將一個連通區域細化成一個像素的寬度，同時保持圖像的形態學特征，主要用于特征提取和目標拓撲表示。從圖2可以很直觀地看出骨架提取的特點。

圖2 骨架提取示意圖

結合骨架提取的特點可以將顆粒的軌跡進行細化，得到單像素寬度的軌跡圖，也就是像素精度的跡線。在此基礎上進行軌跡長度計算要準確得多，且對于彎曲軌跡也更能區分各像素點處速度方向的細微區別。為得到效果更好的軌跡骨架圖，需要對原圖依次進行去噪、自適應閾值分割、閉運算、去除小顆粒及骨架提取等操作，主要的處理流程如圖3所示[15]。

2.1 基于軌跡骨架圖的速度提取

在原理介紹部分已經提到，速度計算的前提是計算運動長度。在獲得軌跡的單像素寬度跡線之后，通過連通區域分割函數可以識別出每條軌跡上的所有像素點，傳統算法采用跡線起點與終點之間的距離作為長度，這樣在處理彎曲軌跡時就會產生較大誤差。本文提出類似于求線積分的求長度算法，首先將每2個像素點之間的距離求出來，然后迭加得到總的軌跡長度，2種算法的對比如圖4所示。

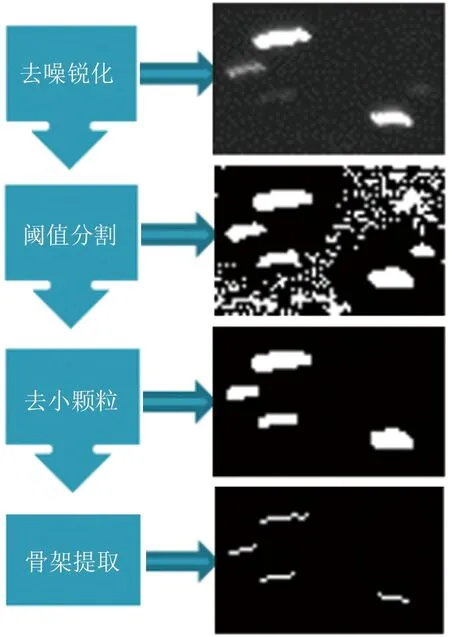
圖3 圖像處理主要流程[15]

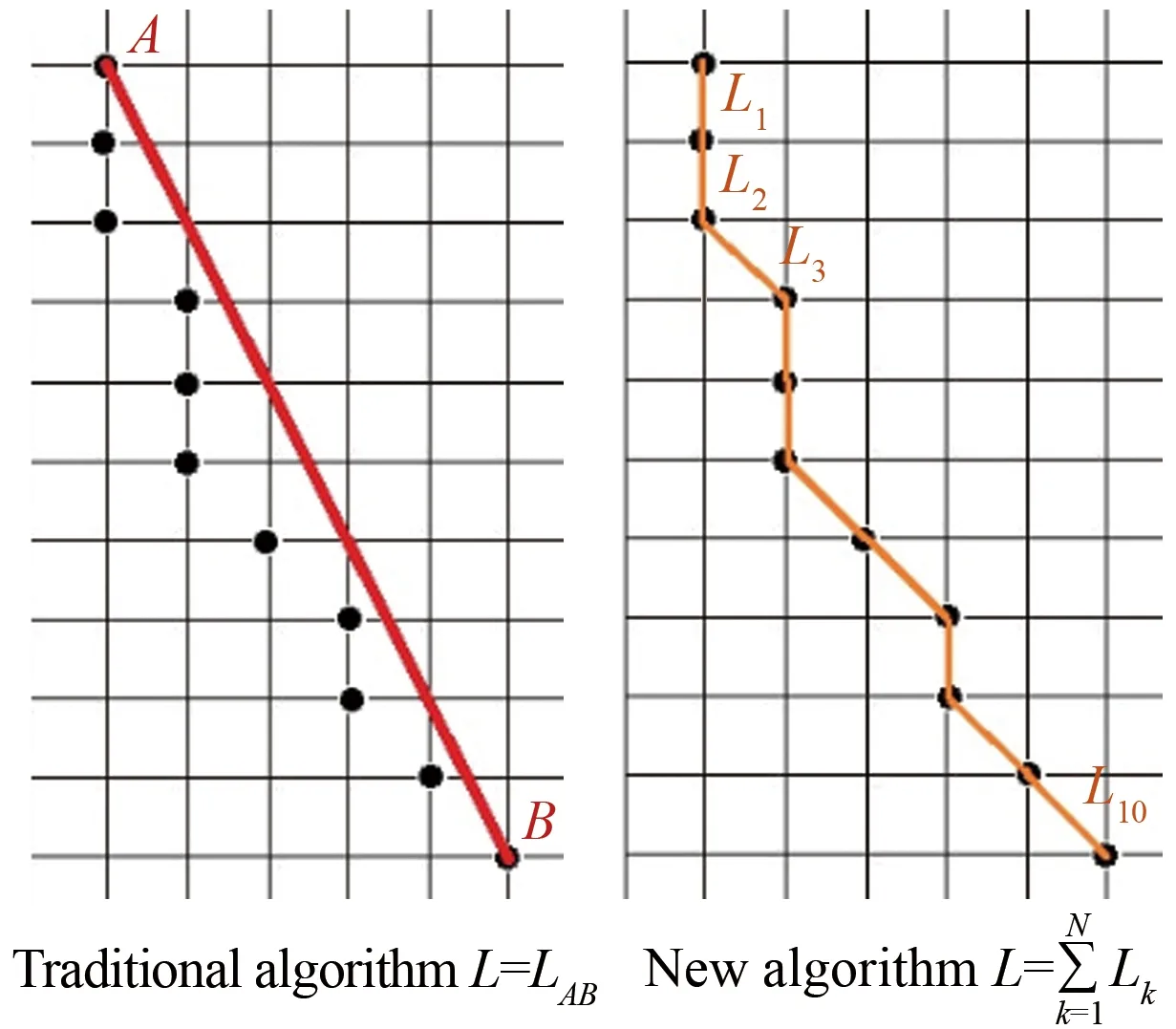
圖4 新舊算法求軌跡長度的對比

Fig.4Thedifferenceontrajectorylengthsbetweenthetraditionalandthenewalgorithm

對于速度的方向，以往的計算方式是采取軌跡首尾相連的一條直線作為方向向量，如圖4中的舊算法。但這種方法在處理彎曲軌跡的時候會產生很大誤差，且一條軌跡上所有的點共享一個速度矢量，十分籠統。因此，提出了求跡線切線的方法，將像素點前后若干個像素點之間的割線近似視為切線,并作為軌跡上該點的速度方向，不僅對于彎曲軌跡能很好地提高精度，而且同一條軌跡上各個像素點的速度矢量也有區分，能很好地體現顆粒的實際運動過程。圖5顯示了新舊算法求速度方向的區別，新算法(左側)各個像素點處的速度由其切線決定，能更好地顯示粒子的流動過程，舊算法(右側)則過于籠統，所有像素點的速度矢量完全相同，不能體現實際的流動狀態。此外，若將軌跡上各個點處的速度矢量逐幀播放，也能更清晰生動地顯示顆粒的動態流動過程。

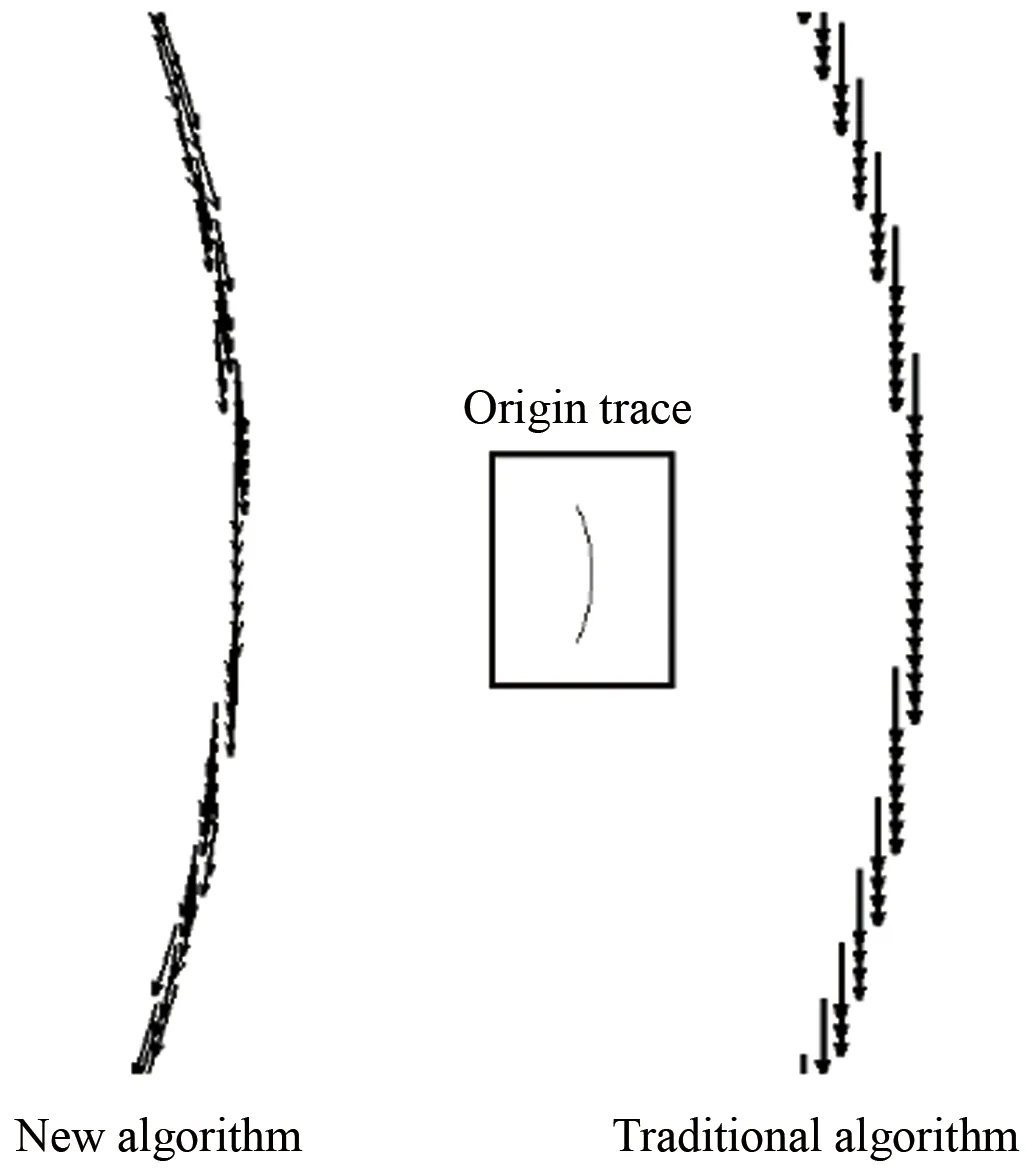
圖5 新舊算法求速度方向的對比

Fig.5Thedifferenceonvelocitydirectionbetweenthetraditionalandthenewalgorithm

圖6為新舊算法在計算不同彎曲程度軌跡時的精度對比。從仿真圓形軌跡上截取不同弧長的軌跡，然后分別采用2種算法求長，并與弧長的理論值進行對比。圖中，橫坐標為軌跡的弧長，也代表了軌跡的彎曲程度，縱坐標為軌跡長度。紅色圓點為舊算法計算的長度，藍色三角點為新算法計算的長度，黑色方點為實際弧長。由圖6可見，在弧長較低，即軌跡接近直線的情況下，2種算法的結果均十分接近真值；隨著弧長的增加(即軌跡彎曲程度增加)，新算法則逐漸體現出了優勢。

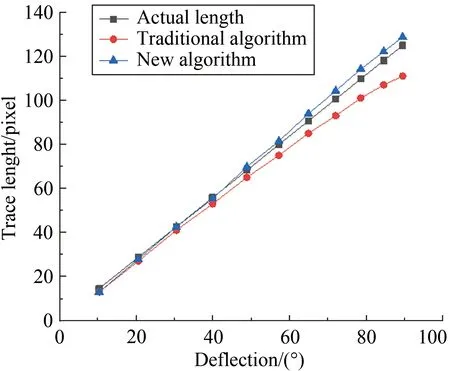
圖6 2種速度提取算法精度比較

Fig.6Accuracycontrastbetweenthetraditionalandthenewalgorithm

2.2 速度二義性的判斷

在前文的敘述中，速度的計算忽略了一個很重要的問題，就是速度二義性的判斷。對一條軌跡來說，一般有2個端點，那么軌跡是從端點A運動到B還是從B運動到A是2種完全不同的情況，所以需要對該問題進行判斷。下面提供2種方法：一種是利用流體的角速度進行判斷，另一種則利用多幀圖像之間的運動關系進行判斷。

2.2.1 角速度判別法

角速度判別法是一種利用右手螺旋定則來確定軌跡運動方向的方法。如圖7所示，有一組圍繞同一中心點進行旋轉的4條軌跡，此時執行前述的速度提取流程后，上下2條軌跡的速度方向會保持一致(水平向右)。但實際上，由于這是一組旋轉軌跡，上下2條軌跡的方向應該相反。為使同一旋轉中心的一組軌跡旋轉方向保持一致，使用角速度判別法進行判斷。圖7中，通過右手螺旋定則可以知道上方軌跡的角速度垂直紙面朝里，而下方的角速度垂直紙面向外，二者互相矛盾，通過改變其中一條軌跡的速度矢量即可解決速度二義性問題。在實際執行過程中可預先定義軌跡的旋轉方向(順時針或逆時針)，從而統一各個軌跡的速度方向，消除二義性。

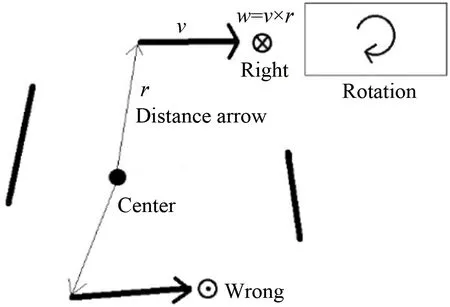
圖7 角速度判據

對于直線運動狀態，可以將旋轉中心點選在垂直于軌跡的無窮遠處。此外，對于復雜的流動，可以通過選取多個旋轉中心分別進行角速度判別，由于過程比較復雜，故方法具有一定的局限性。

2.2.2 多幀連續曝光圖像匹配

單幀圖像很難解決二義性問題，而多幀圖像則可以。因此，在相機進行第一段曝光之后，立刻進行第二段曝光，這樣得到2幀在時間序列上幾乎銜接的圖片，由于2幀圖片的時間先后順序已知，就能很方便地求出顆粒的速度方向。

在多幀圖像匹配方法中，關鍵在于2幀圖片中同一條軌跡的匹配識別[16]。由于2次曝光之間的時間間隔非常短暫，所以2段軌跡理論上是能首尾相連的。實際處理中，對于第一幀圖片里的所有軌跡，于2個端點附近搜索其在第二幀圖片中是否有軌跡，搜索半徑由2段曝光之間的間距時間以及流場的速度決定。為了保證在搜索半徑中只有該軌跡的下一幀軌跡出現，因此顆粒密度不宜太大。此外，考慮到邊緣部分的軌跡可能由于進出視場而導致無法匹配，故應提前將邊緣部分的軌跡剔除。圖8展示了2幀連續曝光圖片(曝光時間為7ms，間隔時間為0.077ms)匹配并疊加的過程，其軌跡匹配率為84.5%。

圖8 2幀圖片的匹配與疊加過程

在完成2幀圖片之間的軌跡匹配之后，速度二義性就解決了。舉例來說：假設AB是第一幀圖片的某條軌跡，端點分別是A和B，而CD是該軌跡在第二幀圖片上的位置，端點分別是C和D；若B和C是2條軌跡的連接點，則軌跡的方向就依次是A—B—C—D。

多幀圖像匹配之后，不僅解決了速度二義性問題，同時，由于得到了不同時間序列上的速度值，也能因此獲得加速度。

2.3 二值化與骨架提取的誤差分析

基于骨架提取的軌跡處理算法可以分成2部分：圖像處理部分和速度計算部分。速度計算部分的誤差已經在2.1節進行了描述，此處對二值化和骨架提取的誤差進行分析。

2.3.1 二值化過程誤差分析

單閾值分割通常采用Ostu (最大類間方差)閾值，其通過圖像灰度將圖像分為背景和目標，通過最大化背景和目標之間的類間方差來找尋最優閾值。考慮到單閾值分割在灰度分布不均的情況下并不適用，故使用了自適應閾值分割。這是一種多閾值分割方法，通過分析像素周圍局部范圍的灰度特性來決定該像素點的閾值，能夠使閾值分割后的圖片保留更多信息。

二值化過程的誤差分析實驗采用了仿真的運動模糊圖片，如圖9所示。根據實際射流實驗圖片，將仿真顆粒圖像的背景灰度設為40，目標灰度設為200，粒徑為5pixel，將顆粒圖像進行卷積并添加方差為0.008的高斯加性噪聲即得到仿真運動模糊圖像，卷積核則由運動長度決定。

圖9 多種運動的仿真運動模糊圖片

仿真實驗的結果如圖10所示，可見隨著運動長度的增加，2種閾值分割的誤差均顯著下降，且自適應閾值分割的誤差要明顯低于Ostu 閾值分割。

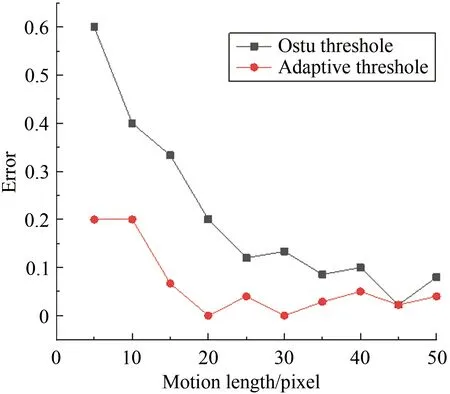
圖10 不同二值化過程的誤差

2.3.2 骨架提取過程誤差分析

骨架提取過程將二值圖轉變成骨架圖，故誤差分析過程采用仿真的軌跡二值圖(由一系列圓形疊加形成的類似于橢圓的圖形)進行一系列仿真實驗。初步認為骨架提取的結果受軌跡大小、軌跡長短軸比、軌跡方向(位置)三方面的影響。實驗過程中分別計算二值圖與骨架圖中軌跡對應的運動長度。在二值圖中，運動長度為軌跡的長度減去寬度；在骨架圖中，軌跡長度即為像素距離迭代求和的長度。仿真實驗結果如圖11～13所示。

從圖11可以看出骨架提取結果與軌跡的方向無關；從圖12和13看出，骨架提取操作對運動長度的影響很小。進一步考察原始數據發現，在所有情況下，骨架圖中的運動長度都比二值圖的運動長度大一

個固定值1，這是由于長度計量的起點不同所導致的。舉例來說，假設有一個僅包含一個像素點的軌跡，其長度應該為1，但長度減去寬度卻等于0，從而導致了二者相差1的現象，這種情況在實際應用過程中統一即可。

圖11 骨架提取結果與軌跡方向的關系

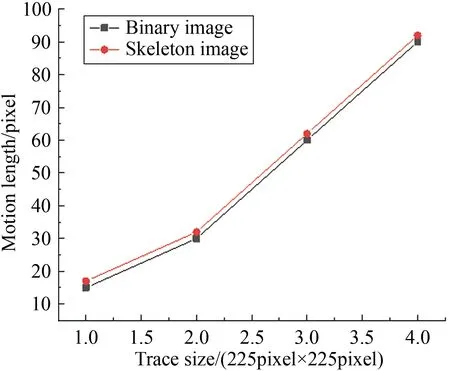
圖12 不同軌跡尺寸下二值圖與骨架圖的運動長度

Fig.12Motionlengthofbinaryandskeletonimageondifferenttrajectorysizes

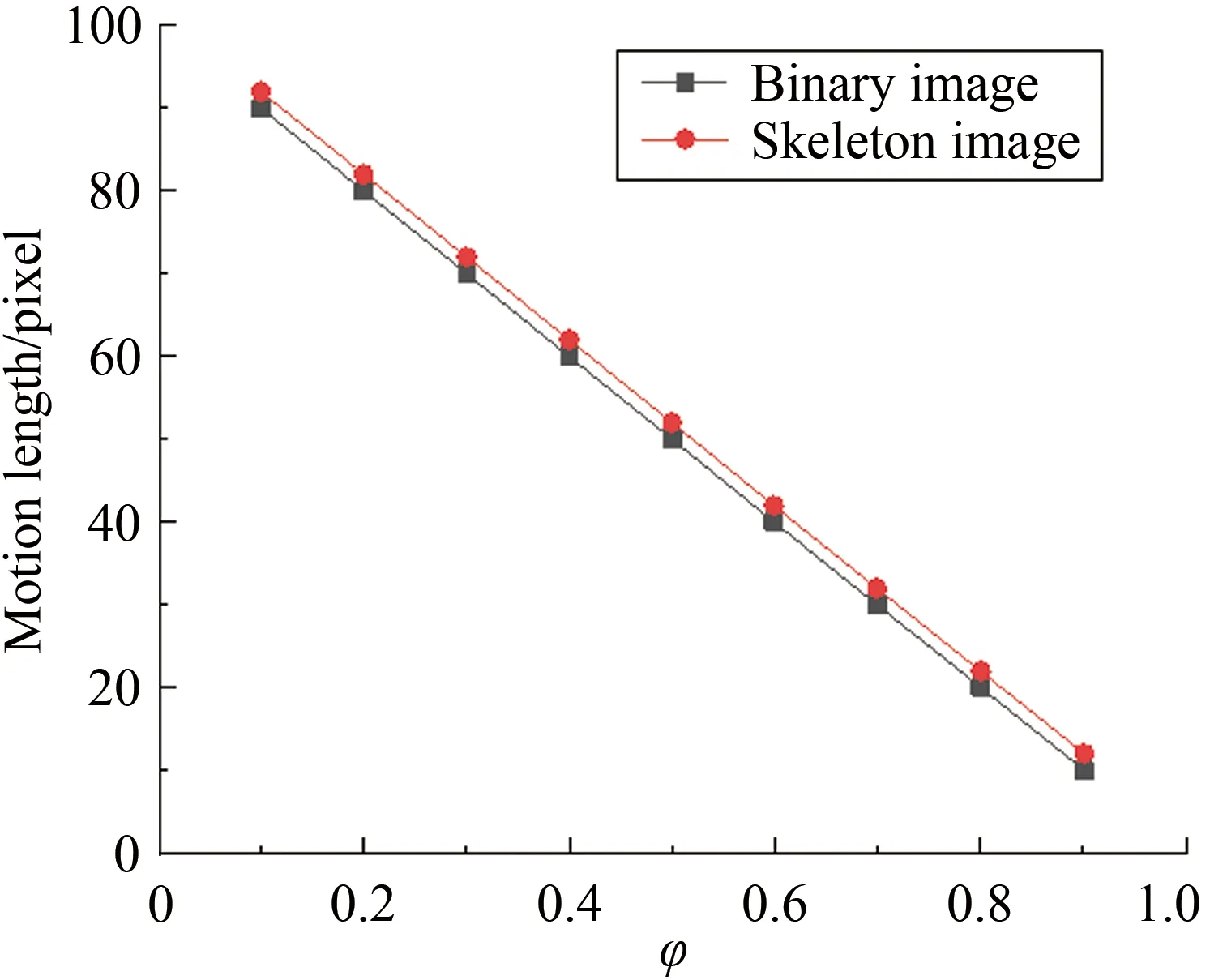
圖13 不同長寬比(φ)下二值圖與骨架圖的運動長度

Fig.13Motionlengthofbinaryandskeletonimagewithdifferentwidth/lengthrate(φ)

3 流場重構算法

在執行了上述軌跡處理算法之后，可以得到每條軌跡的速度信息。然而多數情況下實際需要的是整個流場的速度信息，因此需要進行流場重構工作。

3.1 RBF插值法重構流體速度場

從隨機的數據擬合出整個平面場的信息屬于數學上插值的范疇。選用徑向基函數(Radial Basis Function,RBF)插值的方法得出流場的速度場。該插值方法的基本假設是插值點的函數值受插值源函數值影響，且影響程度與插值點和插值源之間的距離有關，其數學表達式如下：

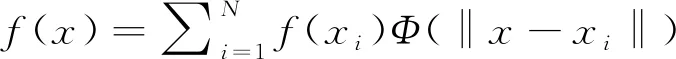
(2)

根據不同應用實例，可以選取不同的距離系數函數Φ以達到最佳的插值效果。比較多種函數的插值效果，從中選取名為“multiquadric” 的距離系數，其距離系數函數如下：

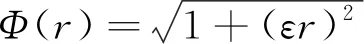
(3)

考慮到流體速度場的特點，任意一點的速度受來流方向速度值的影響大于下游方向速度值的影響。需要在RBF插值的基礎上進行類似于“迎風插值”的優化。優化的基本思想是在插值點的上游增加對插值點的影響；在插值點的下游減弱對插值點的影響。因此，可以構建迎風修正系數函數ψ，ψ的值由插值點與已知點之間速度向量的夾角決定，當夾角為銳角時，ψ大于0，對結果進行增強；當夾角為鈍角時，ψ小于0，對結果削弱。其表達式如下:

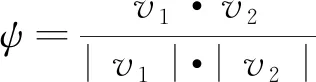
(4)

修正后的插值表達式如下:

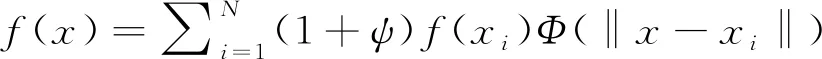
(5)

3.2 RBF插值的誤差分析

對插值的誤差進行分析，采用仿真輸出的流場結果，隨機選取一定的數據點之后進行插值，分析插值結果與原流場的差別即可。原流場與插值流場的速度云圖如圖14所示。

為了量化2幅圖之間的相似度，以便更直觀地獲知不同插值方法的優劣，定義2幅圖像之間的平均距離δ，如式(6)所示。δ越大，表示兩者之間的差別越大，δ越小，表示兩者越為接近。

(6)

表1顯示了選用不同插值函數并采用“迎風插值”優化之后的插值結果的平均距離。從中可以看出基于 “multiquadric” 并采用“迎風插值”優化之后得到插值效果是最好的，與肉眼直觀相符。

圖14 仿真流場(a)與插值流場(b)對比

Fig.14Contrastbetweensimulationflowfield(a)andinterpolationflowfield(b)

表1 插值結果誤差分析Table 1 Error analysis on interpolation

4 處理結果

為驗證本文算法在實際情況下的適用性，采用射流實驗中拍攝的圖片作為處理對象，如圖15所示。實驗中射流出口流速為0.15m/s，拍攝部位為射流口上部的卷吸區域。射流口位于圖片右下方，視場大小為2.88mm×3.86mm。圖16展示了軌跡骨架圖，圖17和18分別是最終速度場的云圖和矢量圖。

圖15 原始圖像

在速度云圖中，每個像素點處的顏色代表了該處的速度大小，因而能直觀地看出速度場在空間上的能量分布；在速度矢量圖中，箭頭方向為速度方向，箭頭長度表征了速度大小，從而可以看出流場整體運動趨勢。

圖16 軌跡骨架圖

圖17 速度云圖

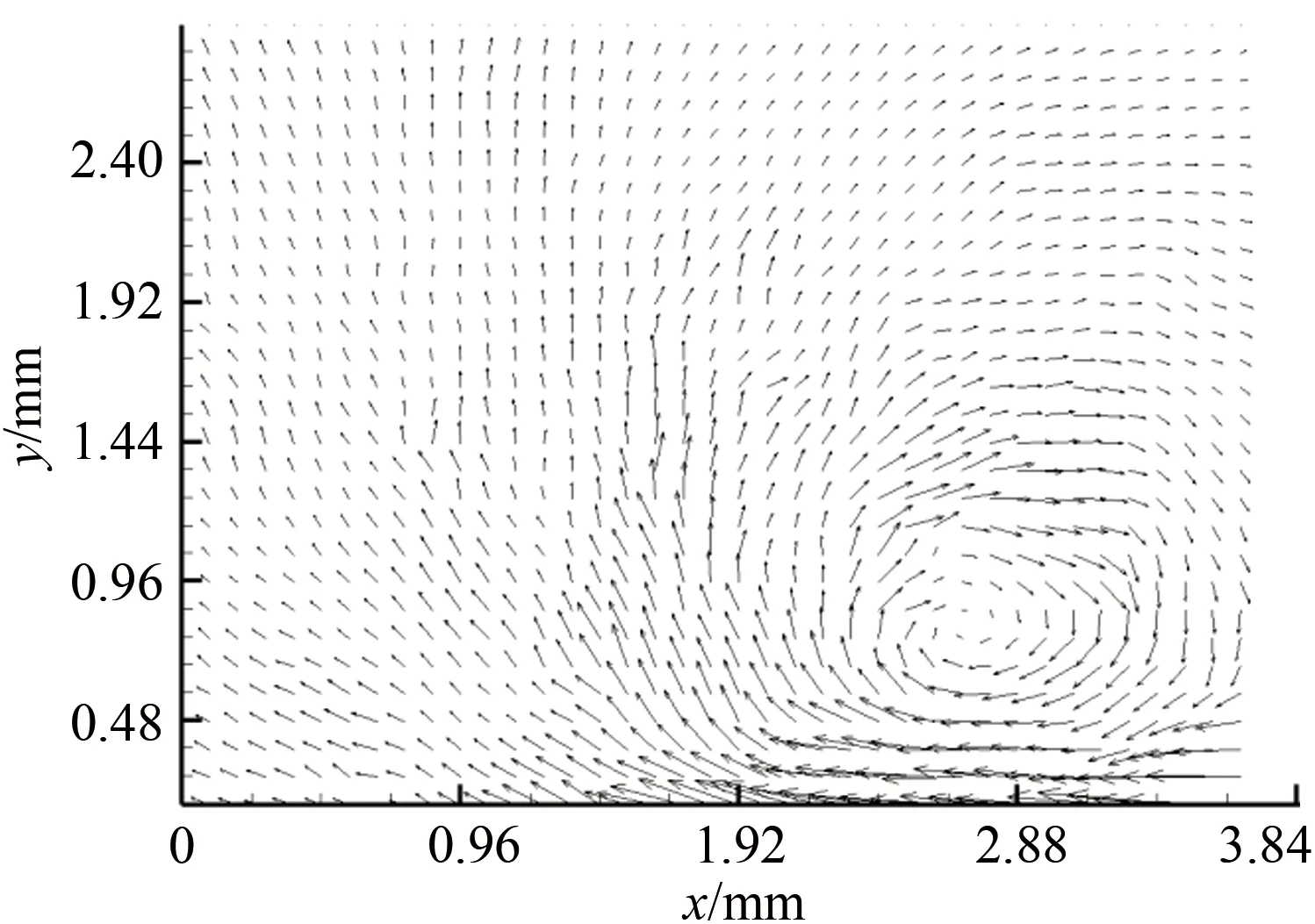
圖18 速度矢量圖

為驗證實驗結果的可信度，利用插值后的速度場來計算速度的散度場。考慮到此處速度場并非連續，因此采用變分方式來計算散度，同時假定流場為二維流動，散度計算公式如下：

(7)

采用云圖方式展示計算的散度場，如圖19所示，由于常溫常壓下水流可視為不可壓流動，速度的散度應處處為零，圖19中大多數散度值接近為零，少數幾處出現稍大的散度值(正值或負值)，不過總體上結果符合事實。

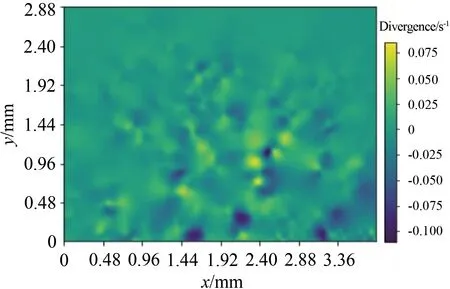
圖19 速度的散度云圖

5 結 論

為獲取顆粒的速度分布，針對單幀單曝光圖像的處理提出一種顆粒軌跡處理算法。通過骨架提取獲得軌跡的跡線，然后對跡線的像素坐標進行迭代求和來計算軌跡長度，同時通過求跡線的切線來計算速度方向。相比傳統算法，該算法在速度大小和方向上均有更高精度，且不同于傳統算法一條軌跡一個速度矢量的模式，該算法的一條軌跡可以獲得軌跡上任意點處的速度矢量，大大提高了信息利用率。

在得到原始的離散速度場之后，利用迎風優化后的RBF 插值算法，可以重構一個相對連續且平滑的全分布流場，可在此基礎上計算加速度、散度等參數，方便后續研究；也可以很方便地與CFD 等仿真模擬結果進行比較。

本算法處理結果的精度上限取決于閾值分割過程，因而需要在拍攝過程中調整曝光時間、光源、顆粒濃度等因素，盡可能提高所拍攝圖像中軌跡的清晰度，以期達到好的閾值分割效果，減少圖片中的干擾軌跡，從而獲得更高精度的結果。