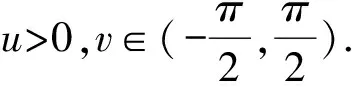具平坦歐氏邊界的局部凸浸入超曲面

王寶富

(四川大學數學學院, 成都 610064)

1 Introduction

Firstly, we recall some notions on an immersed hypersurface in differential geometry. An immersed hypersurface M is defined asx:M→Rn+1, whereMis ann-dimensional differential manifold.

(i) If for eachp∈M, there is a neighborhood Up?Msuch thatx(Up) lies on one side of the tangent hyperplaneπatx(p), then we callx(M) a locally convex hypersurface.

(ii) For a locally convex surfacex(M), ifπ∩x(Up)={x(p)} for eachp∈M, then we callx(M) the locally strongly (strictly) convex hypersurface.

Ifx(M) isC2, the definition “locally strongly convex” is equivalent to “locally uniformly convex”. Generally, to prove thatx(M) is locally strongly (uniformly) convex hypersurface, we only needs to prove that its second fundamental form is positive definite.

(iii) If for eachp∈M,x(M) lies on one side of its tangent hyperplane atx(p), then we callx(M) a globally convex hypersurface, or (simply) a convex hypersurface.

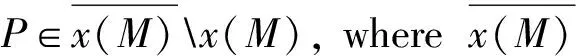
An equivalent definition of the immersed locally convex hypersurface is stated in Ref.[1].

Definition1.1A locally convex surface M inRn+1is an immersion ofn-dimensional oriented and connected manifold N (possibly with boundary) inRn+1,i.e., a mappingT:N→M ?Rn+1, such that for anyp∈N, there exists a neighborhoodωp?N such that

(i)Tis a homeomorphism fromωptoT(ωp);

(ii)T(ωp) is a convex graph;

(iii) the convexity ofT(ωp) agrees with the orientation.

A hypersurface is assumed to be locally uniformly convex, namely it has positive principal curvatures[2].

Generally the geometric property of a hypersuface boundary is closely related to the completeness of the immersed hypersuface itself. So it is interesting to study the boundary character of a locally uniformly (strongly) convex immersed hypersurface. In Ref.[3], the author classifies the Euclidean boundary points as two classes and gives many hypersurfaces with the first class and the second class Euclidean boundary point respectively.

In this paper, we will prove that there exist locally strongly convex immersed surfaces inR3such that their boundaries lie in a plane but the surfaces is not globally convex, which are different from an existing conclusion. Moreover, we give a method to construct similar hypersurfaces inR4,i.e., we get the following theorem:

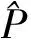
Forn=2, there is an Example 1.3 constructed by author and involved in Ref. [4], it is totally different from Lemma 2.1 of Refs.[5-6].

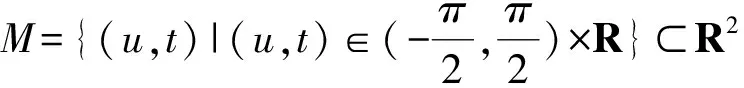
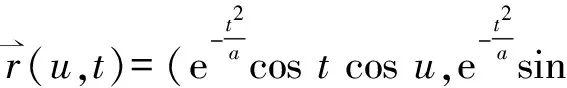
(1)

wherea>0 be a constant. The Euclidean boundary ofx(M) is a line segment

The surface is convex at all the points corresponding tot=0,i.e., at any points of the half circle

x(M) is obviously not globally convex (see Fig.1 and Fig.2).

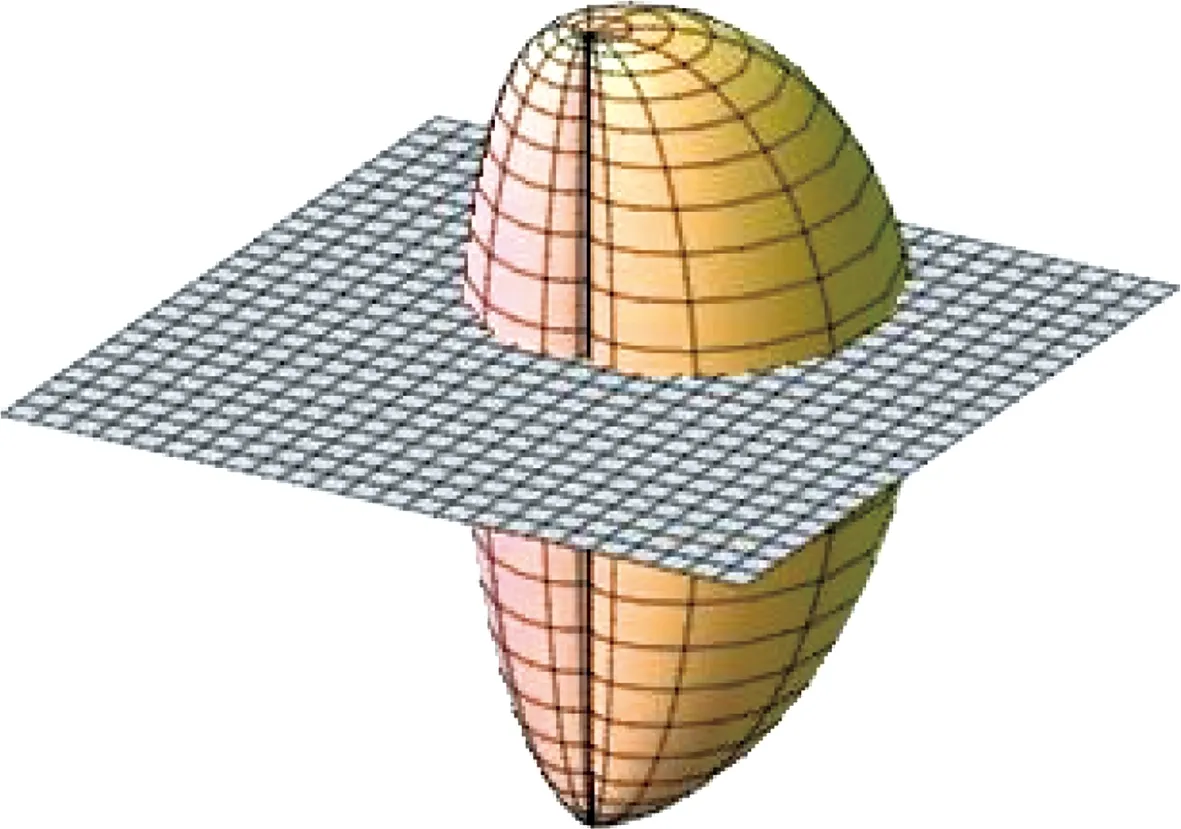
Fig.1 A sketch map of x(M) for a=2

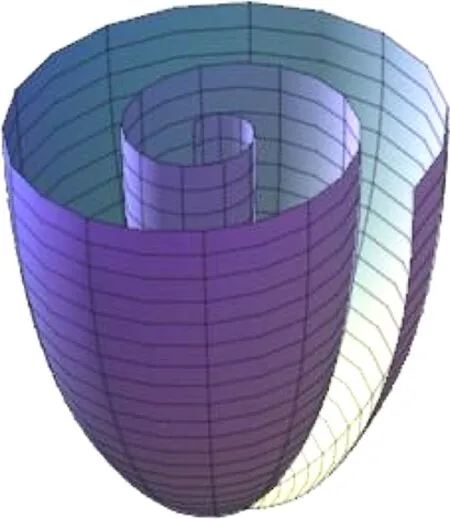
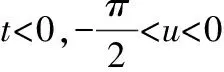
In the next section, we will construct a new locally strongly (uniformly) convex surface inR3(n=2) and some new examples forn>2 which are satisfying Theorem 1.2. Then we complete the proof.

2 New examples

LetM?R2be an open set andx:M→R3be an immersed surface inR3defined by

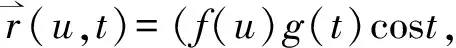
f(u)g(t)sint,h(u))

(2)

wheref(u),g(t),h(u) are smooth functions to be determined later.By direct calculations we have

A normal vector ofx:M→R3is

h′f(g′ cost-gsint),ff′g2).

Denote

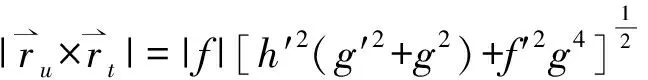
|f|A,

Next, we have

2g′cost-gsint,0).

Then we get the second fundamental form ofx:M→R3, which can be expressed as

II=Lu udu2+2Lu tdudt+Lttdt2,

where

Lu u=A-1g2(h″f′-h′f″),Ltt=

A-1fh′(-gg″+2g′2+g2),Lut=0

(3)

Define the functiong(t) as following.

(4)

whereb>0 is a constant to be determined later.A direct calculation shows thatg(t) isC2. For

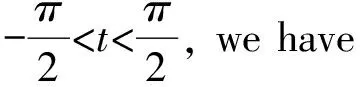
-gg″+2g′2+g2=g2+2g′2-

(5)

Letf(u)=u,h(u)=eu,u>0 in (2). We get

Luu=A-1g2eu>0

(6)

Ltt=A-1ueu(-gg″+2g′2+g2)>0

(7)

letM={(u,t)|(u,t)∈(0,+)×R}?R2,x:M→R3be defined by

(8)

for the surfacex(M)?R3.

? By (6), (7), it is locally strongly convex.

? Whenu→0,(0,0,1) is the unique Euclidean boundary point of the surface (see Fig.3), so the boundary ofx(M) lies in a plane.

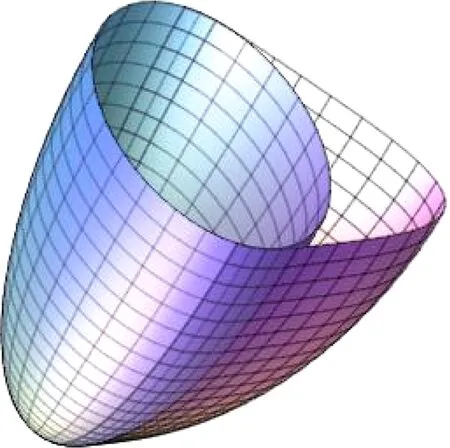
Fig.3 The unique Euclidean boundary point of the surface

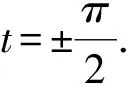
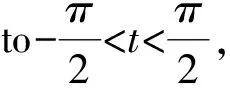
Therefore, This example satisfies Theorem 1.2.

It is easy to construct the high dimensional hypersufaces satisfying Theorem 1.2. Here we give a method as follows ( here we only considern=3).

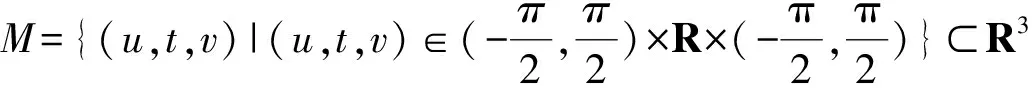
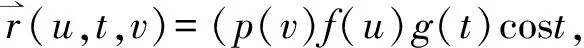
p(v)f(u)g(t)sint,h(u),k(v))

(9)

as before, where

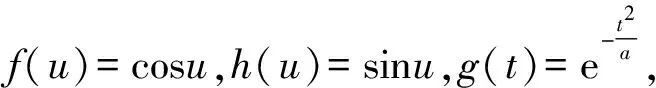
andp(v),k(v) will be determined later. We have

The normal vector ofx:M→R4is

k′h′pf(g′cost-gsint),k′p2ff′g2,

pp′f2g2h′).

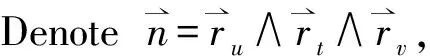
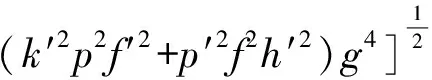
where

We have

2g′cost-gsint,0,0),

Then we get the coefficients of the second fundamental forms ofx:M→R4as follows

(10)

(11)

(12)

(13)

Lut=Lvt=0

(14)

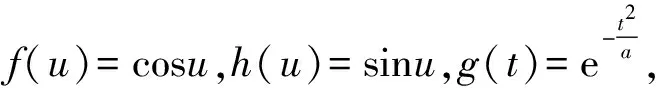
Luu>0,Ltt>0,Lvv>0

(15)

A-2g4cos2ucos2v(1-sin2usin2v)>0

(16)

where

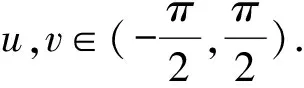
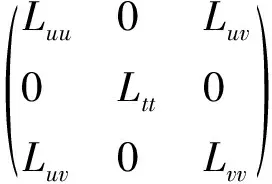
(17)

This means that the immersionx:M→R4is locally strongly convex. The boundary ?x(M) is

lies in a plane. One may easily check that the hypersuface defined by the above formula (9) satisfies Theorem 1.2.

Similarly, based on the above new example, one may get

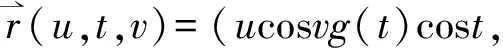
ucosvg(t)sint,eu,sinv)

(18)