淺談小學數學教學中還原法解題策略
阮能才
摘要:新課程標準要求注重學生于小學階段初步形成幾何直觀和運算能力,發展形象思維與抽象思維,讓學生在學習活動參與中發展合情推理和演繹推理能力。而還原法解題就注重學生逆向思維的培養,能夠讓學生創造性地思維訓練模式在數學中得到充分發展。
關鍵詞:逆向思維;還原法;流程圖;解題策略
中圖分類號:G623.5?文獻標識碼:B文章編號:1672-1578(2020)01-0152-01
蘇聯教育心理學家克魯提茨基說:“在一種逆向思路中,思想并不是必須沿著完全相同的思路進行,而是向著相反的方向運動。”這里“向相反的方向運動”指的就是逆向思維。在小學數學教學中,滲透逆向思維具有一定的重要性,逆向思維的訓練可以排除順向思維的困難,并且能夠培養學生的創造性,挖掘學生思維的潛能,使看似簡單的問題卻能給學生帶來深刻的思考,激發學習興趣。
小學數學教學中,有些問題的解答需要學生立足于最后的結果,采用還原方法利用加、減、乘、除等方法的互逆關系,從后往前逐步推算,進而使問題得到解決。通常需要利用還原法解答的問題都具有一定的特征,即問題敘述的未知量是經過一系列已知推理而得到的已知量,最終是求原來的未知量。
模型一:從單個對象出發?循序漸進
“單個對象”即一道完整的題目中,主語和總量有且只有一個,主語和總量無論經過怎樣的變化,最終所求的對象還是這個主語的總量。例如:媽媽買來一些桔子,小明第一天吃了這些桔子的一半多2個,第二天吃了剩下的一半少3個,第三天吃了剩下的一半,現在剩下5個桔子。求媽媽買的桔子一共有多少個?
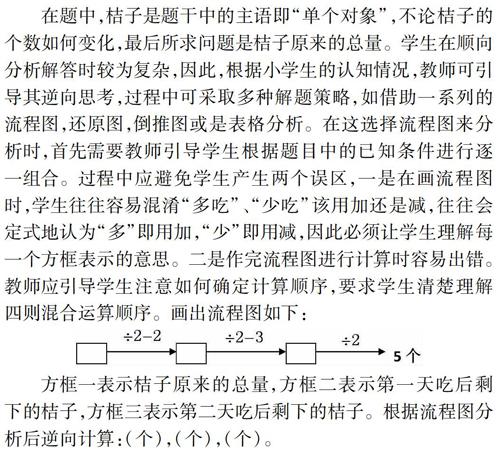
在題中,桔子是題干中的主語即“單個對象”,不論桔子的個數如何變化,最后所求問題是桔子原來的總量。學生在順向分析解答時較為復雜,因此,根據小學生的認知情況,教師可引導其逆向思考,過程中可采取多種解題策略,如借助一系列的流程圖,還原圖,倒推圖或是表格分析。在這選擇流程圖來分析時,首先需要教師引導學生根據題目中的已知條件進行逐一組合。過程中應避免學生產生兩個誤區,一是在畫流程圖時,學生往往容易混淆“多吃”、“少吃”該用加還是減,往往會定式地認為“多”即用加,“少”即用減,因此必須讓學生理解每一個方框表示的意思。二是作完流程圖進行計算時容易出錯。教師應引導學生注意如何確定計算順序,要求學生清楚理解四則混合運算順序。畫出流程圖如下:
方框一表示桔子原來的總量,方框二表示第一天吃后剩下的桔子,方框三表示第二天吃后剩下的桔子。根據流程圖分析后逆向計算:(個),(個),(個)。
模型二:多個對象?靈活運用
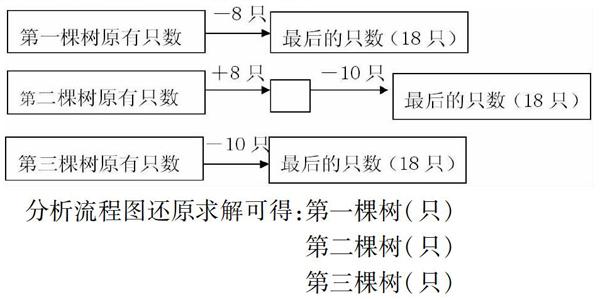
“多個對象”即題干中出現多個主語,多個主語同時發生變化,且總量也發生變化,最終所求的未知量不只一個。例如:有54只鳥分別停在三棵樹上,有8只從第一棵飛到第二棵樹上,又有10只從第二棵樹上飛到第三棵樹上。這時,三棵樹上鳥的只數相等。從題干分析可知:主語分別是第一棵樹、第二棵樹、第三棵樹,并且三棵樹上的總量均發生變化,最終是分別求三棵樹上原來有多少只鳥。當涉及“多個對象”的還原問題時,學生往往不知如何下手,教師應以合作者、引導者身份幫助學生理清題中的數量關系,進行逆向推理。由于最終三棵樹上鳥的只數是相等的,因此,我們可以根據這一線索入手,把54只鳥進行3等分,便可求出最終每棵樹上鳥的只數,即(只),再根據已知條件畫出流程圖如下:
分析流程圖還原求解可得:第一棵樹(只)
第二棵樹(只)
第三棵樹(只)
模型三:不同對象??確定核心
“不同對象”即在一個題干中不只一個主語,其與“多個對象”的區別在于題干中的已知條件看似是“單個對象”,但問題中所求未知量卻不同,其實質是存在隱藏的已知量,且會導致學生在解題時產生偏差。因此,解決此類還原問題應注重對題干中已知條件的充分分析。
逆向思維的培養,不僅有助于學生發現新知識,打破順向思維的定式,更有利于培養學生全面考慮問題,在思考的過程中達到求同存異。通過對學生逆向思維能力的培養,可使學生能夠從不同角度分析問題,探求不同的思路,運用不同的解題方法求解生活中的實際問題。在這樣的教學過程中,不僅是培養學生發散思維,更重要的是能夠使學生在解決問題時求異求新。
在數學的課堂中滲透逆向思維,發展學生的思維能力,鍛煉學生的動手實踐能力是新課標改革的要求。還原法既符合小學生的順向思維,又符合其直觀思維,教師有意識地引導學生生成逆向思維,從而使學生不但學到了數學知識,開發了智力,還能夠讓學生利用逆向思維多角度地解決生活中的數學問題,達到學以致用的目的。
參考文獻:
[1]?馬麗君.淺談小學數學教學中滲透的數學思想與方法[J]赤峰學院學報(自然科學版).2014(01)17-18.
[2]?毛凱捷.小學數學解題教學中還原法的運用[J]教書育人教師新概念.2016(06):56.
[3]?姜嫦君,劉靜霞.小學數學教學中數學思想方法的滲透[J].延邊教育學院學報.2010(02):106-108.

