不同粒度煤的瓦斯解吸擴散規律實驗研究*

韓恩光，劉志偉，冉永進，馬樹俊，李志強

(1.中煤科工集團重慶研究院有限公司，重慶 400037； 2.河南理工大學 安全科學與工程學院，河南 焦作 454000)

0 引言

研究煤粒瓦斯解吸擴散規律，對于瓦斯含量測定和煤與瓦斯突出預測與防治都有重要意義。影響煤粒瓦斯解吸擴散的因素主要有煤樣破壞程度、煤樣變質程度、煤樣粒度、煤樣水分、煤樣溫度和初始吸附平衡壓力。針對煤樣粒度對煤粒瓦斯解吸擴散規律的影響，楊其鑾[1]實驗研究表明，煤粒存在極限粒度，瓦斯放散初速度隨粒度的增大而減小，煤粒達到極限粒度后，瓦斯放散初速度保持不變。實驗中最大極限粒度為陽泉一礦煤樣5.4 mm;周世寧[2]認為煤粒的極限粒度隨煤質而變化，大體在0.5～10 mm之間;聶百勝等[3]使用平均粒度0.214～1.42 mm的煤樣研究煤瓦斯解吸擴散規律，研究表明煤樣粒度愈大初始有效擴散系數愈大，動力學擴散參數反而越小，相同解吸時間內的甲烷解吸率越小;賈彥楠等[4]使用0.2～3 mm煤樣進行試驗，研究結果驗證了極限粒度理論的正確性;秦躍平等[5]、劉彥偉等[6]、陳向軍等[7]在研究瓦斯解吸擴散規律時所采用煤樣粒度均在6 mm以內。前人針對粒度大于10 mm的煤樣實驗研究較少，為了證實和完善極限粒度理論，本文以煤粒度毫米級至厘米級的5種不同粒度煤樣為研究對象，開展瓦斯解吸擴散規律的研究。

關于煤的瓦斯放散規律，從20世紀60年代起眾多國外學者[8-11]進行了研究，提出了經典單孔隙擴散模型，雙孔隙擴散模型。楊其鑾等[12]導出了經典模型的近似式來計算擴散系數，但不能準確地描述煤中瓦斯擴散全過程；劉彥偉[13]將雙孔模型推廣至三孔模型，但是增加了待定參數，計算難度增大。本文以不同粒度的煤樣為研究對象，煤粒中存在小至幾納米大至毫米級孔隙。因孔隙大小不同，煤中瓦斯擴散類型不同。為了準確地描述不同粒度煤樣瓦斯擴散規律，本文采用李志強等[14]提出的動擴散系數模型對煤中瓦斯擴散過程進行描述和分析。

1 實驗煤樣和實驗方法

1.1 實驗煤樣

煤樣取自河南焦煤集團九里山礦，在實驗室將其破碎、粉碎和篩分后,分別得到1～3，>3～6，10～20，>20～30，>30～40 mm粒度煤樣，并進行工業分析、低溫液氮和壓汞實驗，測得煤樣水分(Mad)為1.13%，灰分(Aad)為14.7%，揮發分(Vdaf)為17.3%，視密度為1.49 g/cm3，孔隙率為5.25%，吸附常數a值為26.98 cm3/( g·r)，b值為1.69 MPa-1·r。

1.2 實驗裝置及實驗過程

實驗裝置采用H-Sorb 2600T高溫高壓吸附/解吸擴散儀，該裝置由高低溫變頻控制單元、吸附平衡單元、真空脫氣單元、解吸測量單元和數據實時采集單元組成，如圖1所示。

圖1 H-Sorb 2600T高溫高壓吸附/解吸擴散儀Fig.1 H-Sorb 2600T high temperature and high pressure adsorption / desorption diffuser

取一定質量干燥后煤樣裝入樣品管內，將裝有煤樣的樣品管安裝在儀器左側的樣品預處理區，然后在樣品預處理區對其進行真空干燥，真空干燥結束后，取下樣品管，安裝在儀器樣品測試區。采用純度為99.99%的高壓甲烷對實驗系統進行充氣，使煤樣吸附甲烷，若未達到預設吸附平衡壓力，則繼續充氣，直至煤樣達到預設吸附平衡壓力，設置吸附平衡壓力分別為0.5，2.0 MPa，待煤樣吸附平衡后，分別進行5種粒度煤的等溫解吸擴散，即可得到不同粒度煤隨時間變化的瓦斯解吸量。

1.3 實驗數據處理

將實驗所得的t時刻單位質量煤的瓦斯解吸量Qt′(含損失量)根據式(1)轉換為標況下單位瓦斯解吸量。

(1)

式中：Qt為標況下單位瓦斯解吸量，cm3/g；Qt′為實測單位瓦斯解吸量，cm3/g；p為實驗環境壓力，Pa；ta為環境溫度，℃。

將標況下單位瓦斯解吸量Qt與極限解吸量Q∞相比，得到其解吸率(Qt/Q∞)。其中，極限解吸量按Q∞=Q-Qa計算，實驗條件下的Q，Qa均按式(2)計算：

(2)

式中：Q為初始總含氣量，cm3/g；a，b為吸附常數；p為吸附平衡壓力，MPa；Ad為灰分，%；Mad為水分，%；ρ為煤視密度，g/cm3；φ為孔隙率；tw為吸附平衡溫度，℃；計算實驗室大氣壓下終態平衡含氣量Qa時，以實驗室大氣壓代替式(2)中的吸附平衡壓力p。

2 試驗結果及分析

2.1 粒度對瓦斯解吸量的影響

初始吸附平衡壓力0.5，2.0 MPa條件下，不同粒度煤樣瓦斯解吸量Qt隨時間變化如圖2所示。

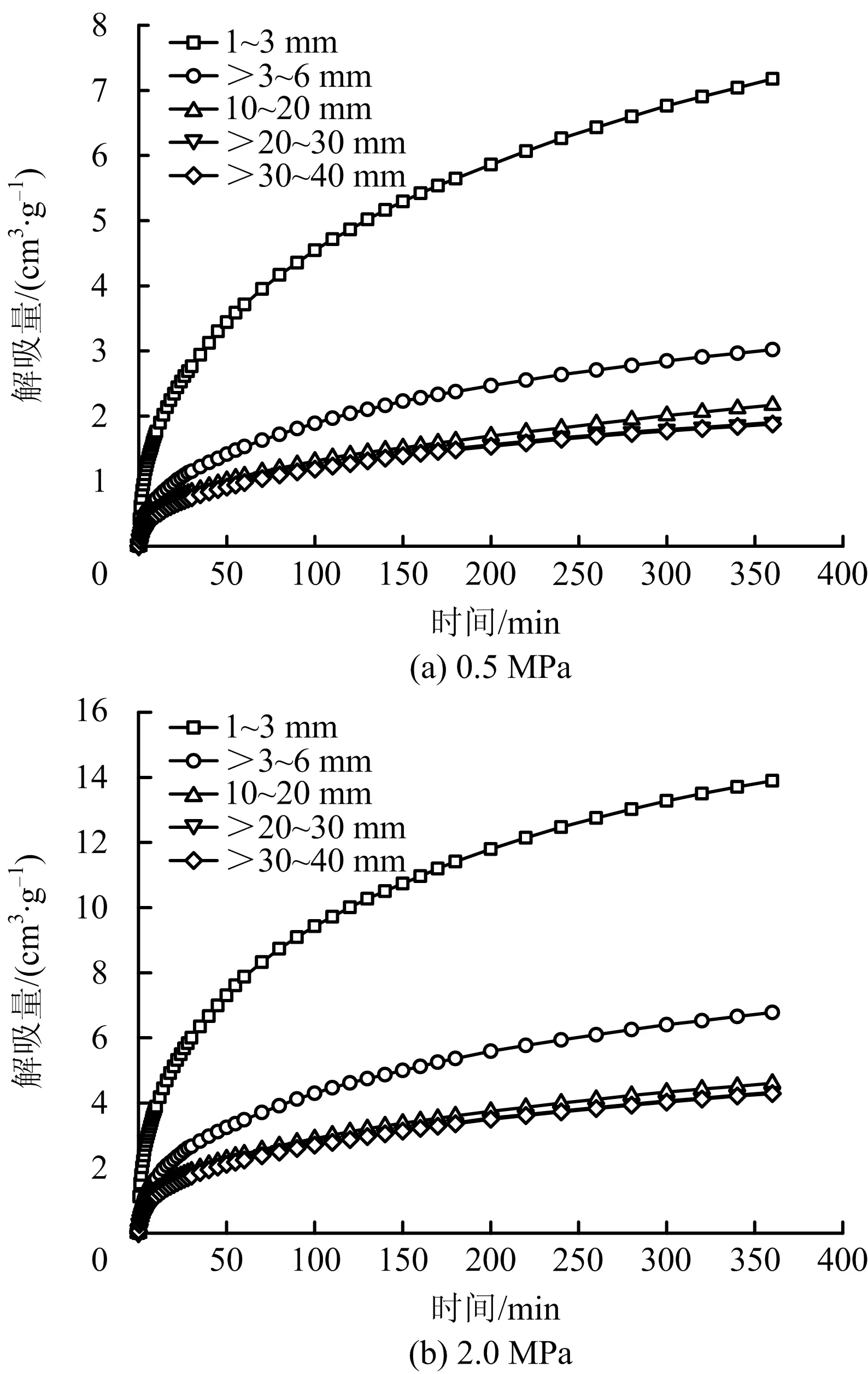
圖2 不同粒度煤瓦斯解吸量變化Fig.2 Variation curves of gas desorption amount of coal with different particle sizes

將圖2中不同粒度煤的瓦斯解吸量進行對比：0.5 MPa吸附平衡壓力下，360 min時，1～3 mm粒度煤單位瓦斯解吸量為7.18 cm3/g；>3～6 mm粒度單位瓦斯解吸量為3.02 cm3/g，相比1～3mm粒度煤樣降幅57.93%；10～20 mm粒度煤單位瓦斯解吸量為2.17 cm3/g，相比>3～6 mm粒度煤樣降幅28.18%；>20～30 mm粒度煤單位瓦斯解吸量為1.90 cm3/g，相比10～20 mm粒度煤樣降幅12.38%；>30～40 mm粒度煤單位瓦斯解吸量為1.88 cm3/g，相比>20～30 mm粒度煤樣降幅1.21%。

結果表明，相同時間段內煤的單位瓦斯解吸量隨粒度的增大呈現逐漸減小的趨勢；煤粒度從毫米級增至厘米級過程中，煤樣單位瓦斯解吸量減小明顯；厘米級煤樣隨著粒度增大煤樣單位瓦斯解吸量降幅較小。2.0 MPa吸附平衡壓力下實驗結果與之類似。

2.2 粒度對瓦斯解吸率的影響

初始吸附平衡壓力分別為0.5，2.0 MPa，不同粒度煤的瓦斯解吸率(Qt/Q∞)隨時間變化如圖3所示。

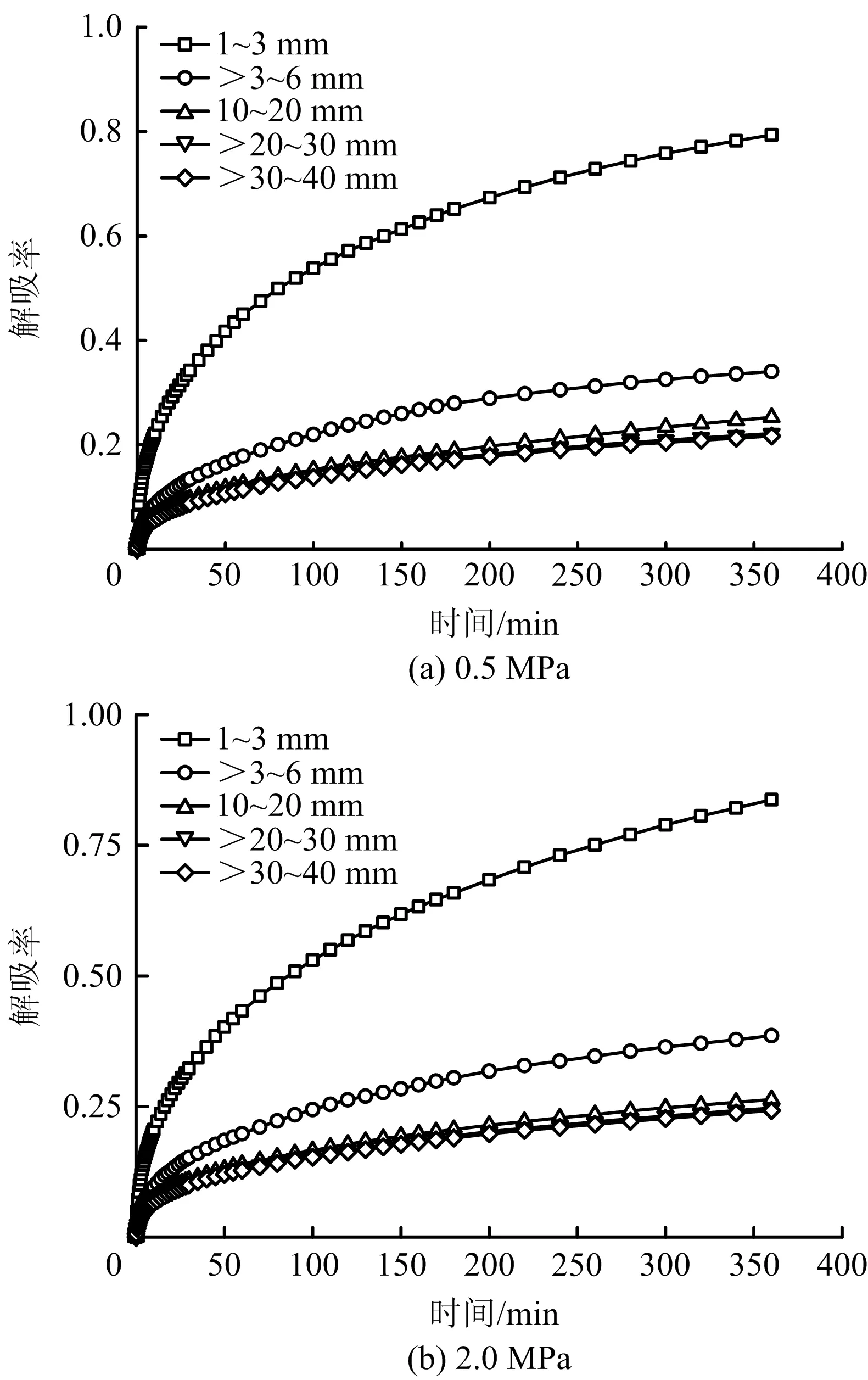
圖3 不同粒度煤瓦斯解吸率變化Fig.3 Variation curves of gas desorption rate of coal with different particle sizes

將圖3中不同粒度煤的瓦斯解吸率進行對比：0.5 MPa吸附平衡壓力下，360 min時，1～3 mm粒度煤瓦斯解吸率最大，達到0.793；>3～6 mm粒度煤瓦斯解吸率為0.340，相比1～3 mm粒度煤樣降幅57.07%；10～20 mm粒度煤瓦斯解吸率為0.253，相比3～6 mm粒度煤樣降幅25.71%；>20～30 mm粒度煤瓦斯解吸率為0.221，相比10～20 mm粒度煤樣降幅12.38%；>30～40 mm粒度煤瓦斯解吸率為0.217，相比>20～30 mm粒度煤樣降幅1.96%。

結果表明，相同時間段內煤的瓦斯解吸率隨粒度的增大呈現逐漸減小的趨勢；煤粒度從毫米級增至厘米級過程中，煤樣瓦斯解吸率減小明顯；厘米級煤樣隨著粒度增大煤樣瓦斯解吸率降幅較小。2.0 MPa吸附平衡壓力下實驗結果與之類似。

3 不同粒度煤樣瓦斯解吸擴散特征

3.1 動擴散系數模型及計算結果

建立動擴散系數模型的基本假設:煤粒為各向同性的球形顆粒；煤基質孔隙系統由非均質、多尺度的孔隙構成，并且多級孔隙連續分布；瓦斯在多級孔隙中擴散時，仍遵循連續介質力學假設以及質量守恒定律。

煤體瓦斯擴散數學模型表達式為：

(3)

式中：Qt，Q∞分別表示t時刻瓦斯累計解吸量和標況下瓦斯極限解吸量，cm3/g；D0為t=0+時的初始擴散系數，cm2/s；r為煤粒半徑，cm；β為衰減系數，s-1；t為時間，s。

由動擴散系數模型所求得的動擴散系數平均值Da(cm2/s)，即為經典擴散模型的擴散系數D[14]。考慮到煤粒度對擴散的影響，定義初始有效擴散系數D0e與平均有效擴散系數Dae，其中Da，D0e，Dae計算公式如下：

(4)

(5)

(6)

式中：r0為煤粒的平均半徑，mm。

采用式(3)～(6)，對不同粒度煤樣在不同吸附平衡壓力下的瓦斯解吸實驗數據進行計算，求得初始擴散系數D0、平均擴散系數Da、初始有效擴散系數D0e及平均有效擴散系數Dae，見表1。

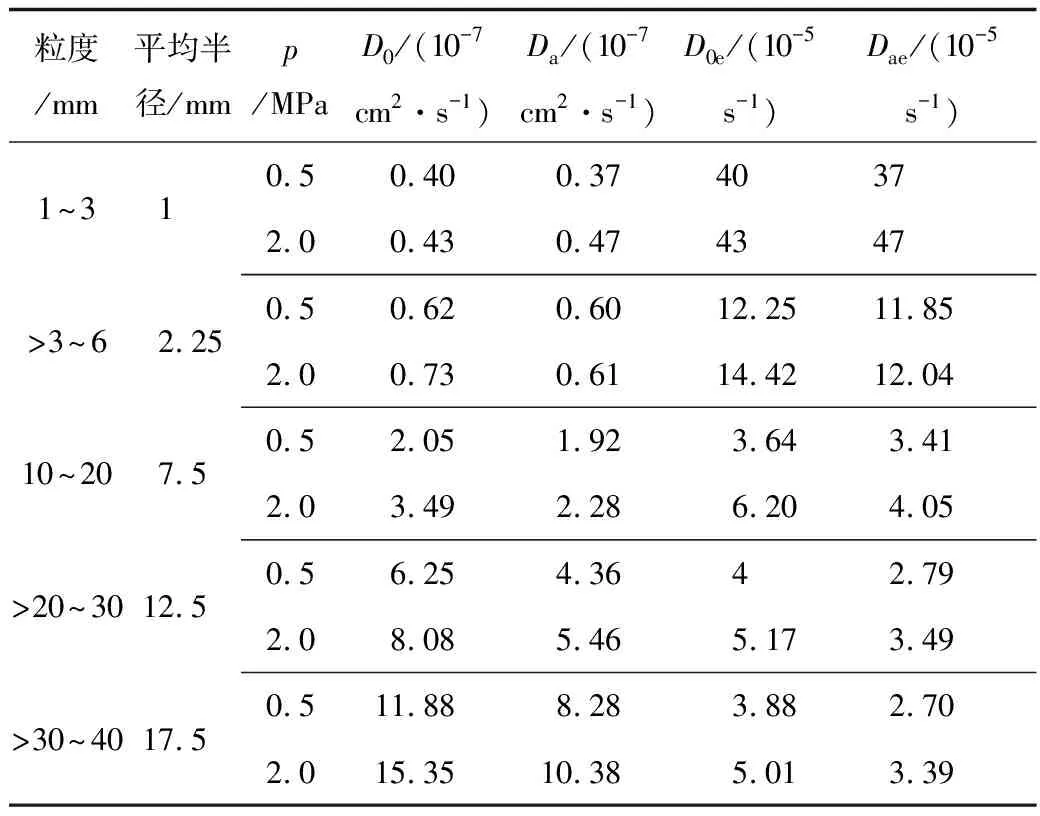
表1 不同粒度煤瓦斯擴散系數計算結果Table 1 Calculation results of gas diffusion coefficient of coal with different particle sizes

3.2 初始/平均有效擴散系數與粒度關系

將表1中初始有效擴散系數D0e、平均有效擴散系數Dae隨平均半徑變化關系繪制成圖4～5。

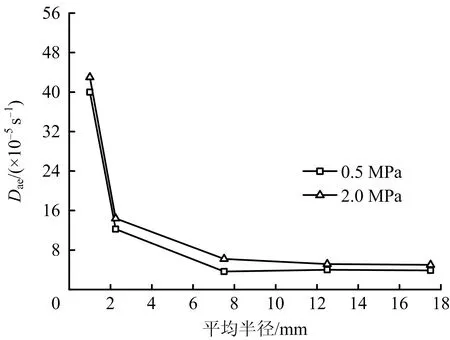
圖4 初始有效擴散系數D0e值隨平均半徑變化關系Fig.4 Relationship between initial effective diffusion coefficient D0e and mean radius

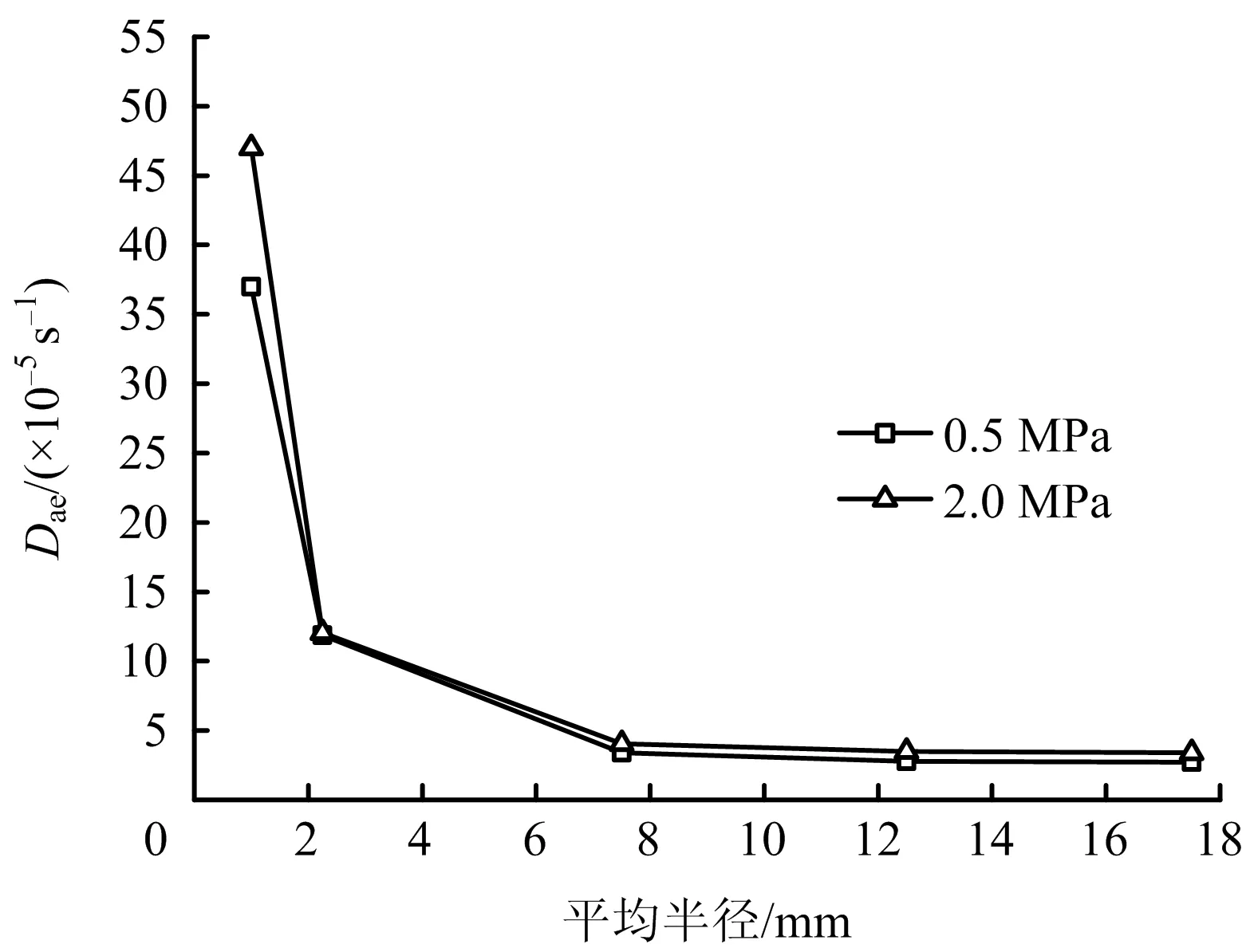
圖5 平均有效擴散系數Dae值隨平均半徑變化關系Fig.5 Relationship between average effective diffusion coefficient Dae and mean radius

由表1及圖4～5可看出，同初始吸附平衡壓力下，煤粒度在毫米級范圍內，初始有效擴散系數D0e和平均有效擴散系數Dae隨粒度的增大快速下降。煤粒度為厘米級時，初始有效擴散系數D0e和平均有效擴散系數Dae隨粒度的增大基本保持不變。

依據以上結果，煤樣粒度達到厘米級時，初始有效擴散系數D0e和平均有效擴散系數Dae隨粒度的增大基本保持不變，證明煤樣粒度已經達到了極限粒度，由此可得煤的極限粒度為毫米級，即極限粒度小于10 mm。

4 結論

1)相同時間段內煤的單位瓦斯解吸量隨粒度的增大呈現逐漸減小的趨勢。煤粒度從毫米級增至厘米級過程中，煤樣單位瓦斯解吸量減小明顯。厘米級煤樣隨著粒度增大煤樣單位瓦斯解吸量降幅較小。

2)相同時間段內煤的瓦斯解吸率隨粒度的增大呈現逐漸減小的趨勢。煤粒度從毫米級增至厘米級過程中，煤樣瓦斯解吸率減小明顯。厘米級煤樣隨著粒度增大煤樣瓦斯解吸率降幅較小。

3)同初始吸附平衡壓力下，煤粒度在毫米級范圍內，初始有效擴散系數D0e和平均有效擴散系數Dae隨粒度的增大快速下降。煤粒度為厘米級時，初始有效擴散系數D0e和平均有效擴散系數Dae隨粒度的增大基本保持不變。

4)依據實驗所得煤的單位瓦斯解吸量與煤樣粒度的關系、煤的瓦斯解吸率與煤樣粒度的關系以及由動擴散系數模型所求得的初始有效擴散系數D0e與平均有效擴散系數Dae與煤樣平均半徑的關系。從煤的解吸擴散規律角度證實極限粒度理論的正確性，得出煤的極限粒度小于10 mm。