基于最優空時自適應處理的箔條云干擾抑制方法

李 冉, 栗 蘋, 賈瑞麗

(北京理工大學 機電學院,北京100081)

0 引言

空時自適應處理最初只是針對機載多通道動目標顯示(MTI)雷達,目前已被諸多需要進行自適應傳感器時域和空域處理的領域所采用[1-2],且從地面環境和水下環境等其他應用環境中都得到了很好的發展[3-4]。空時處理的目的就是在雜波或干擾占據的角度——多普勒處放置一個抑制凹口,該凹口將取決于感興趣的目標角度——多普勒信息[5]。

箔條是一種常用的無源干擾手段。目前針對箔條云干擾的抑制方法可以分為以下幾類[6-8]:

a)基于箔條極化特征的抗干擾方法,文獻[6]定義了共極化比和垂直共交極化比,提出了以共極化比和垂直共交極化比為聯合鑒別量的抗箔條干擾方法;

b)基于箔條頻率特性的抗干擾方法文獻[7]:建立了箔條錐動的回波信號模型,綜合考慮了箔條絲錐動對雷達回波信號頻譜的影響,現有文獻已經對箔條云回波特性有了多角度廣泛研究,但一般都只考慮了箔條云中單根箔條造成的影響并只進行簡單的矢量加和,缺乏對箔條云整體響應的分析;

c)基于箔條統計特性的抗干擾方法,文獻[8]選取了六個參數,并利用模糊函數構造箔條云統計特性來分辨箔條云,這六個參數分別為反射率、差分反射率、互相關因子、線性化的差分相位、反射率標準差和差分相位標準差。

針對箔條云整體空時域特性的研究尚很欠缺,本文基于箔條云的統計模型,研究了箔條云的空時域特性,且利用空時自適應處理理論推導了抑制箔條云回波的最優空時處理方法。

1 箔條云的空時域特性

箔條云完全散開的條件下,箔條云后向散射回波電壓服從瑞利分布,相位服從均勻分布[7]。基于空時自適應處理(STAP)的前提為無源干擾波是均勻的,且滿足不相關復反射率因子的廣義平穩過程。而箔條云回波不僅取決于發射天線方向圖,也與箔條云回波固有特性有關。定義ηj為

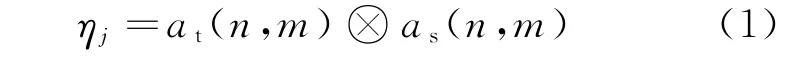
式中:ηj為考慮了箔條云回波電壓幅度和相位的復隨機向量;{at(n,m)}服從瑞利分布;{as(n,m)}服從均勻分布;n為理想的天線單元個數;m表示m個脈沖重復間隔(PRI)時間延遲。

箔條云模型的數學期望為

箔條云回波滿足不相關復反射率因子的廣義平穩過程模型。

根據空時自適應原理,為了方便分析只考慮一個N陣元構成的均勻線性陣列,相干處理間隔內由固定脈沖重復間隔的M個脈沖組成。對于一個理想角度—多普勒矢量S,那么一個確定波束形成器的權矢量w可以由線性方程組w's=1,w'j1=0…w'jNM=0得到。當箔條云存在時,可采用統計信號處理的手段來解決確定性零餡的局限性問題。特別地,箔條云干擾可視為隨機過程,則通過統計最優化過程可得到最優空時波束。首先利用STAP原理分析箔條云的空時域特性。STAP系統應用多接收通道的電子掃描天線,這組陣列天線通過測量各通道線性相位差對回波進行空域采樣,不同相位參數對應不同信號到達方向。

選取第1通道為參考通道,則第n通道的特定到達方向的相位可表示為

式中:τn為回波在參考通道和第n通道間的時延;ω為角頻率,ω=2πf,f為傳播信號頻率。

如圖1所示,根據天線與箔條云的幾何關系可得

式中:dn為箔條云相對于第n通道相位中心坐標系的位置矢量{dx/n,dy/n,dz/n};{^x,^y,^z}為第n通道相位中心坐標系的單位矢量;k(φ,θ)為單位矢量,方向垂直于箔條云回波;φ為方位角;θ為俯仰角;c是波速。

將(3、4、5)代入(6)可得

圖1 箔條云與陣列天線的幾何關系

式中:cosφcone第n通道相位中心坐標系x軸與單位矢量k(φ,θ)的夾角。

可得空域信號矢量為xs=asss(fs),as為一個隨機數即箔條云相位系數,集合{as}服從均勻分布,fs為空域頻率fs=(dx/m/λ)cosφcone;且空域導向量ss(fs)為

式中:f(as)為as的概率密度;為相位變化方差。

另一面,分析計算箔條云的時域特性。假設傳播信號是一個長度為M的周期脈沖序列,且重復周期為T。定義r0為箔條散射點到天線相位參考通道的距離。由于箔條與雷達的相對運動,導致脈間的距離變化為Δr。因此可得時間延遲τm為

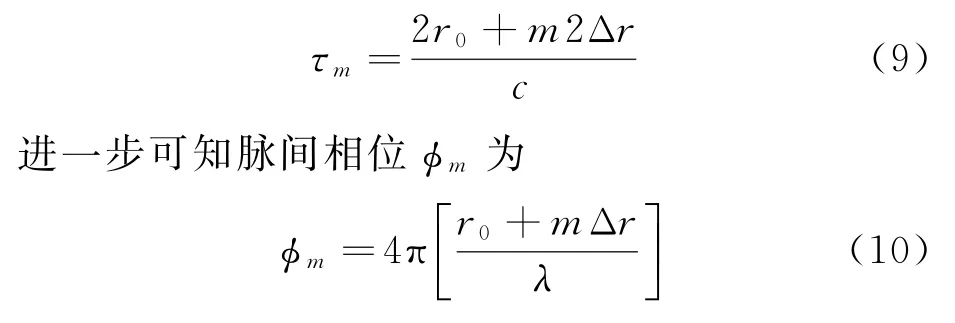
則多普勒頻率fD為

式中:vr為視線速度。

時域信號矢量xt=atst(~fD)為,~fD為歸一化多普勒頻率~fD=fDT,at是一個隨機數即箔條云回波電壓包絡系數,{at}集合服從瑞利分布,時域導向矢量st(~fD)為

式中:f(at)為at的概率密度為箔條云回波幅值方差;Et為箔條云回波電壓幅度均值。

對比式(7)和式(12),箔條回波在空域和時域的響應具有相似的數學表達式。則可得空時信號導向矢量ss-t(fs,~fD)為,?表示Kronecker積:

圖2給出了箔條云空時特性的仿真結果。其中設置N=16,M=14,總自由度為224;干擾噪聲比(JNR)為30 dB,噪聲水平為0 dB;箔條云相位系數{as}服從均勻分布,電壓幅值系數{at}服從瑞利分布,并且方差=1。圖2(a)為箔條云協方差矩陣特征值分布,(b)為基于傅里葉變換的箔條云功率譜估計。由圖2可知,箔條云回波功率譜在空時域呈陡峭的錐型,且在不同角度—多普勒方向上回波功率變化劇烈。

2 最優空時處理抑制干擾技術

利用最優空時處理原理,推導最優空時波速形成器,可以有效抑制箔條云干擾。如圖3所示的空時線性波束形成器,其由N個理想的天線單元——空域自由度和M個脈沖重復間隔(PRI)時間延遲——時域自由度組成。為了最大化信號干擾噪聲比(SINR),需要選擇最優的空時權系數ω[5]。

圖2 箔條云空時特性

權系數ω可表示為

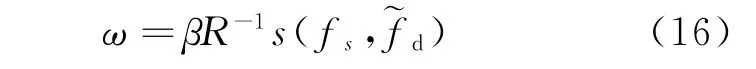
式中:R∈CCNM×NM為NM×NM維干擾和目標的協方差矩陣;β為常數標量并不影響SINR輸出(可由SINR的定義推導此結論,此處不贅述);s(fs,~fd)∈CCNM為NM維期望信號的空時導向矢量,可表示為

式中:s(~fd)為時域導向矢量;s(fs)為空域導向量。

由于干擾響應平方的期望可表示為

因此,可得最優波束成型器的高分辨譜估計為

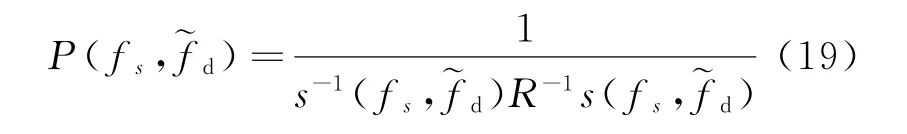
進一步聯合加權處理可以表示為

圖3 空時波束形成器

式中:t=td?ts;t∈RRNM為期望NM維加權;ts∈RRN為N維角度加權;td∈RRM為M維多普勒加權。

3 仿真實驗

為了驗證本文方法的有效性,下面通過仿真實驗方法進行分析,并考察箔條云空時特性修正模型對干擾抑制方法性能的影響。由于實際的干擾環境通常不是先驗已知的,因此利用有限樣本估計的手段去近似得到式(16)中要求的干擾協方差矩陣。在本例中,為保證輸出SINR為最優處理的3 dB左右,至少選取448個理想箔條云回波樣本,且樣本中沒有任何目標信號。然后,采用傅里葉變換對理想箔條云回波樣本進行功率譜估計,將其代入波束成型器的高分辨譜估計式(19),計算得到期望NM維加權t。結果如圖4最優空時波束方向圖所示,箔條云干擾與目標回波存在角度和多普勒頻率加權,其中參數設置為N=16,M=14,JNR為60 d B,β=1。

圖4 最優空時波束方向圖

4 結論

為提高雷達抗箔條云干擾能力,分析了箔條云的空時特性,得到了基于最優空時處理的箔條云干擾抑制方法。結果表明文中提出的干擾抑制方法,可成功對箔條干擾信號進行抑制,從而有效提高雷達對抗箔條云干擾的性能。