低信噪比下LFM-BPSK復合調制信號參數估計

孫富禮, 蔣張濤, 沈 軍, 朱嘉穎

(上海無線電設備研究所,上海201109)

0 引言

在現代電子戰中,低截獲概率(Low Probability of Intercept,LPI)雷達由于采用了大時寬大帶寬的復雜調制信號以及進行功率管理等一系列技術手段,有效提高了雷達的戰場生存能力,近年來得到了廣泛應用。電子偵察接收機需要在沒有先驗信息的復雜電磁環境中截獲敵方輻射源的信號,并對其進行特征分析、檢測識別及參數估計,為后續的電子干擾和攻擊等對抗措施提供基礎。LFM-BPSK復合調制信號不僅具有LFM信號測距精度高和多普勒不敏感的特性,還具有BPSK信號多普勒分辨率及測速精度高的優點。已經廣泛應用于多種雷達中[1]。因此,對LFMBPSK復合調制信號參數估計算法的研究具有重要的現實意義。

在已有的LFM-BPSK復合調制信號參數估計方法中,文獻[2]首先利用時頻曲線擬合法對LFM-BPSK信號進行識別,然后利用離散多項式相位變換法和多尺度小波變換法基于信號重構技術對LFM-BPSK復合調制信號進行參數估計;文獻[3]提出了基于分數階傅里葉變換和ZAM分布聯合估計的參數估計算法,首先估計信號的起始頻率和調頻斜率,然后對解線調之后的信號提取ZAM分布在起始頻率截面的負峰值估計碼元寬度;文獻[4]提出了在高斯噪聲下偽碼一線性調頻復合信號參數估計的方法。文獻[5]則對復合信號參數估計理論的性能進行了分析。但是這些方法都是在高信噪比下才能準確估計出LFMBPSK復合信號的參數。本文首先對LFMBPSK復合調制信號進行平方運算去除相位編碼,將信號變換為LFM信號,為兼顧估計精度和信噪比門限,分段濾波后采用迭代插值分數階傅里葉變換方法估計該LFM信號的起始頻率和調頻系數。在此基礎上重構線性調頻信號,并與復合信號共軛相乘得到基帶BPSK信號,然后采用循環譜相關技術提取碼速率。該方法能夠有效提高低信噪比下信號參數估計的精確度和穩定性。

1 信號模型

LFM-BPSK信號可以表示為

式中:q(t)=1;t∈[0,T0];f0為信號初始頻率;B為信號帶寬;k=B/T為調頻斜率;T=NT0為信號時寬;q(t)為矩形信號;T0為碼元時寬;φ0為二元序列,取0或π。

為直觀地分析LFM-BPSK復合調制信號的特征,選取如下仿真參數:采樣頻率為fs=200 MHz,初始頻率f0=5 MHz,碼元寬度為τc=0.5μs,碼元序列采用Barker碼:101001110。此復合調制信號的時域波形圖及頻譜圖如圖1所示。

圖1 LFM-BPSK復合調制信號的時域波形圖及頻譜圖

由LFM-BPSK復合調制雷達信號的時域波形圖和頻譜圖可以看到,其波形更加復雜,頻譜的分布與線性調頻信號類似但更加動蕩。復合調制雷達信號是通過組合多種調制方式而形成的,能夠融合多種信號的優點,彌補其各自不足之處。與單一調制類型信號相比,復合調制信號能夠獲得更大的時寬帶寬積,具有更好的距離分辨率和速度分辨率,同時提升了低截獲性能,加大了敵方偵察接收機截獲和檢測識別的難度,對傳統雷達偵察接收機造成了嚴峻挑戰。

2 參數估計

2.1 插值優化FRFT原理

FRFT是一種廣義的傅立葉變換,其可以看作是信號在時頻平面內任意旋轉一定角度后在分數階域的投影[6]。

信號x(t)的FRFT定義式為

式中:p為FRFT的階數;α=pπ/2表示旋轉角度;Fp[·]為 FRFT 的算子符號,其核函數Kα(t,u)定義為

式中:Aα=為整數。

在實際應用中,文獻[7]提出了一種分解型快速算法,該快速算法需要進行量綱歸一化處理,將時域t轉換為無量綱的域t/λ,將頻域f轉換為無量綱的域fλ,其中λ=。

量綱歸一化使信號在時域和頻域具有相同的長度L=。將式(2)改為如下形式:

式中:ts=t/λ,分解型離散FRFT可以表示為

式中:M(m,a)=Aα/2L·exp(j·πε1m2)/(2L)2,N(n,a)=exp(j·πε1n2)/(2L)2。 其中:對信號進行了2倍內插,因此需要對最后結果Xα(m/2L)進行1/2倍抽取以得到離散采樣Xα(m/L)。

由FRFT的定義可知,LFM信號將在分數階域形成能量聚集譜,而高斯白噪聲的能量將均勻分布在整個分數階域。因此,線性調頻信號的參數估計的基本思想是在(α,u)二維平面內搜索線性調頻信號的能量聚集峰值點,得到峰值坐標(^α0,^u0),其中m為正整數。各參數估計結果為

式中:fs為采樣頻率;angle[·]為取幅角。

線性調頻信號的參數估計就是在離散化(α,u)二維平面上進行峰值搜索。由于噪聲和離散(α,u)平面的分辨率造成了搜索到的峰值點與真實峰值點之間的偏差,稱搜索得到的峰值點為準峰值點。

分數階u域離散化造成的有限分辨率使得搜索得到的準峰值點與真實峰值點的偏差較大,進而影響到信號參數估計的精確度。而在α域可以通過設置更小的Δα來降低離散化處理帶來的偏差,但是計算量會大大增加。因此,可以考慮通過提高u域離散化處理后的分辨率,解決α域分辨率與運算量之間的矛盾來提高參數估計的精度。

準峰值點的FRFT為

準峰值點在u域的取值為=uk=kΔl/N,由于u域離散化,真實峰值點u0的坐標應該在[(k-1)Δl/N,(k+1)Δl/N]內。基于上述分析,利用階分數階傅里葉變換的函數表達式對u進行插值補償,以得到更精確的坐標。

則有ψ1=ψ0+πcscα'0,ψ2=ψ0-πcscα'0。由之前分析知 (u0-uk)πΔl≤π/2。因此,ψ0∈[-π/2,0],ψ1∈ [π/2,π],ψ2∈ [-3π/2,-π]。根據上述求解得

綜上所述,插值補償后得到的更加精確的峰值點在u域的坐標為

利用插值補償后的^u0進行參數估計,可以有效提高線性調頻信號的幅度、初始頻率和初始頻率的估計精度,由于離散化處理及環境噪聲的影響,對信號相位信息的估計偏差較大。在現代雷達中,雷達信號頻率較高,帶寬較大,通常我們只關注信號的初始頻率和調頻斜率信息。偏差分析可知,當α的搜索步長Δα縮小到10-4時,由α域離散化造成的影響可忽略不計,但是這樣會造成計算量的急劇增加,因此,可以考慮在適當的搜索步長下,對旋轉角度α也進行插值補償以降低峰值搜索準峰值點與真實峰值點的偏差,提高信號參數估計的精確度。

理論上,若α域的分辨率Δα取值足夠小,那么搜索的準峰值點坐標就可以無限接近真實值,但是會產生巨大的運算量。若保證線性調頻信號能夠在u域產生突出譜線的條件下,可以設置較大的搜索步長,對旋轉角度α也進行插值補償的方法,得到的α0的精確估計^α0,可以有效降低運算量。

其 中:X1=,ρ'=1-0.005ρ,ρ″=0.015ρ2-2ρ。

因此,通過插值補償法可以由準峰值點αγ和鄰近準峰值點αγ±1得到峰值點α0的精確估計值。將其代入式(6)可得到精確估計的信號各參數。

2.2 循環譜相關

假設x(t)為循環平穩信號,則其相關函數可以表示為

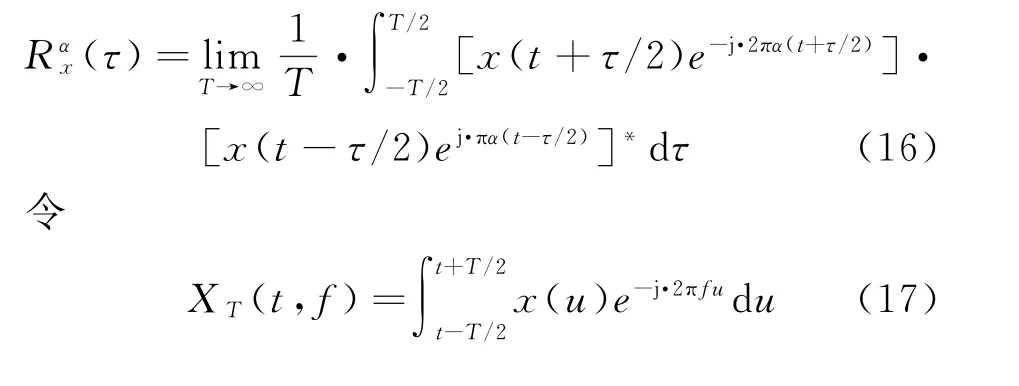
則有

現實中,只能通過在一定的時間內采集有限的數據,通常用離散時域或頻域平滑周期圖法來計算信號的循環譜相關密度函數。由于雷達信號通常頻率較高,在時域進行分析誤差較大,因此本文采用離散頻域平滑方法,其表達式為

式中:Δf=MFs為頻域平滑窗函數;Fs=1/(NTs)是頻域采樣寬度;Ts是時域采樣寬度;aΔt為時間窗函數;Δt=(N-1)/Ts是數據總長度;N是Δt時間內的采樣點數。

BPSK信號可以表示為

式中:{an}為獨立同分布序列,等概率取1和-1。

因此BPSK信號的循環自相關函數為

式中:k為整數;Q(f)為q(t)的傅里葉變換,BPSK信號s(t)的循環譜密度函數為

式中:Q(f)是BPSK信號q(t)的傅里葉變換;Td=1/fd為碼元時寬;fc為信號載波頻率;k為整數,為便于進行分析可令f=0,得出調制信號特征譜(0),可知其絕對值:

由式(26)可以看出,BPSK信號的載波頻率、碼速率和幅度決定了循環譜相關的絕對值。分析Q(f)可知,f=0時取最大值,f＞0和f＜0時逐漸減小。信號特征譜的模值在k=0,α=±2fc時取最大值,在k=0,α=±2fc+1/Td時,取次大值。而且信號循環譜相關的對稱性,可以通過搜索在α＞0時特征譜的模值的峰值對應的頻率來估計二相編碼信號的載波頻率,二相編碼信號的碼元速率的估計則可以根據峰值與相鄰的幅度次峰所對應的頻差來實現。

2.3 參數估計步驟

為了提高LFM-BPSK復合調制信號參數估計算法的精度,需要先對信號進行分段濾波,相位編碼信號對載波的相位進行了調制,在載波相位的跳變位置,信號瞬時頻率會產生突變,如果直接對信號進行分段濾波處理,可能會丟失信號的部分信息,需要對信號做預處理。

首先通過平方倍頻去除LFM-BPSK復合調制信號的相位編碼信息,轉化成帶有噪聲的線性調頻信號,此時,信號的初始頻率與調頻斜率為原信號的2倍。平方倍頻后的信號為

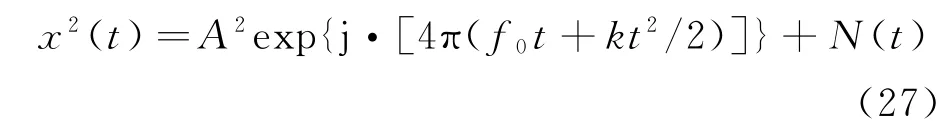
式中:N(t)=2A·exp[j·(2πf0t+πkt2)]·n(t)+n2(t)為LFM-BPSK復合調制信號平方后的等效噪聲。

對原復合調制信號的平方處理導致輸出信噪比降低,將對信號參數估計的精度產生影響。為提高參數估計的精度,采用文獻[9]提出的改進算法對信號進行分段濾波處理。然后采用優化FRFT算法估計平方倍頻后的LFM信號的初始頻率和調頻斜率。具體步驟如下:

a)步驟1:對LFM-BPSK復合調制信號進行平方處理,得到倍頻的LFM信號;

b)步驟2:對倍頻后的LFM信號采用優化的分段濾波算法進行降噪處理;

c)步驟3:利用優化FRFT算法依次進行粗估計和精確估計得到初始頻率和調頻斜率的估計結果為2^f0、2^k;

d)步驟4:由于對原LFM-BPSK復合信號進

假設信號初始頻率及調頻斜率具有較高的估計精度,則Δf→0,Δk→0,則sB(t)信號的表達式為

信號sB(t)為帶噪聲的BPSK信號,因此可利用循環譜相關法估計信號碼速率Rb。具體流程如下:

a)步驟1:計算信號sB(t)的循環譜相關函數(f),得到|(f)|;

b)步驟2:在(α,f)二維平面上搜索α=0,特征譜模值|(f)|對應的頻率fmax,則相位編碼信號的載波頻率的估計值為fc=fmax;

c)步驟3:由步驟2得到信號載頻fc,在頻率f=fc的平面上,在循環頻率α=0的附近求特征譜模值|(f)|的次峰值,其對應的循環頻率分別為α1、α2,則信號的碼元速率的估計值為fd=(|α1|+|α2|)/2。行了平方倍頻處理,因此由步驟3的估計結果除以2便可得原信號的估計值初始頻率^f0和調頻斜率^k。

得到初始頻率^f0和調頻斜率^k的估計值后,對線性調頻信號進行重構:

將重構信號與LFM-BPSK復合調制信號共軛相乘,得到信號sB(n)為

3 仿真實驗

為驗證上述參數估計算法的有效性,構造LFM-BPSK復合調制信號進行仿真實驗,設置信號參數:初始頻率f0=30 Hz,調頻斜率k=200 Hz/s,相位調制碼元寬度為0.1μs,碼元個數為n=1 000,采樣頻率為fs=800 MHz。在信噪比為SNR=5 d B的條件下,分數階傅里葉變換的初始估計及精確估計的三維仿真圖及重構的BPSK信號循環譜相關圖如圖2和圖3所示。

圖2 LFM信號的FRFT粗估計及精確估計三維圖

圖3 重構的BPSK信號循環譜相關圖

圖4 不同算法參數估計的NRMSE曲線

圖5 不同信號參數估計的NRMSE曲線

在信噪比SNR=[-10 dB,10 dB]的區間內,每次間隔1 dB,進行蒙特卡羅仿真實驗200次,分別對本文算法和小波復合算法的參數估計性能進行對比實驗,仿真實驗得到的不同信噪比條件下兩種方法對LFM-BPSK復合調制信號的參數估計的歸一化均方根誤差(NRMSE)如圖4所示。

由圖4所示的仿真結果可以看出,針對LFM-BPSK復合調制信號的參數估計,在相同條件下對信號碼元速率的估計精度均低于信號調頻斜率以及初始頻率的估計精度。小波復合算法和本文采用的算法在信噪比較高時,參數估計的效果都很好,但當信噪比較低時,本文算法對信號各參數估計精度要好于小波復合算法。整體而言,針對LFM-BPSK復合調制信號不同參數的估計精度,本文采用的算法的性能略優。但是,由于優化的分數階傅里葉變換進行了插值補償的優化,計算量比其他算法有所增加,采用在分數階域先大步進粗搜索再縮小范圍進行小步進精確搜索的方法,可以有效提高參數估計的效率。

為驗證參數估計算法的有效性,重新構造一個LFM-BPSK復合信號參數:初始頻率f0=50 MHz,調頻斜率k=300 MHz/s,相位調制碼元寬度為0.1μs,采樣頻率為fs=800 MHz。對兩個信號在相同條件下進行參數估計對比實驗,仿真結果如圖5所示。可以看出,初始頻率和調頻斜率較大的信號2比信號1在信噪比較低時的參數估計誤差略高,且對碼速率的估計誤差要大于對初始頻率和調頻斜率的估計誤差,但兩個信號的參數估計整體效果接近,充分說明本文采用的參數估計算法的穩定性。

4 結論

本文針對LFM-BPSK復合調制信號的特點提出一種FRFT和循環譜相關聯合參數估計方法。對LFM-BPSK復合信號的起始頻率、調頻斜率和碼元速率進行了估計。該方法具有較好的抗噪性和估計精度,在沒有任何先驗知識的條件下即可在低信噪比下精確估計復合信號的參數。

通過對不同信號的仿真實驗結果表明本文方法具有良好的穩定性。但是由于需要在分數階域的二維平面進行峰值搜索,所以運算量較大。