矩形鋼管和矩形鋼管混凝土T形不等寬受拉節點軸向剛度

劉永健，王文帥，馬印平，姜 磊，龍 辛

(長安大學公路學院，陜西西安 710064)

0 引 言

近年來，鋼管節點由于其力學性能優異、制作簡單和造型美觀等優點，在桁架結構中得到廣泛應用[1]。對于鋼管桁架結構，其整體撓度為桿件變形和節點變形之和，其中桿件變形可通過桁架鉸接模型計算得到，而節點變形尚缺乏準確的計算方法。國際管結構協會CIDECT規范[2]建議，對計算得到的桁架變形乘以放大系數1.15來偏保守地考慮間隙節點的變形，而中國現行規范對于節點變形尚未給出規定。因此，有必要對節點變形的計算方法開展研究，而節點變形與節點軸向剛度密切相關，可通過分析節點軸向剛度來研究節點變形。

目前，矩形(箱型)截面在桁架橋中應用較廣[3-5]，但是考慮到矩形鋼管桁架端部受力較大，通常需對其進行局部加強，同時矩形鋼管節點也存在節點承載力較低的問題，因此，學者們提出在矩形鋼管節點內填充混凝土形成矩形鋼管混凝土節點[6-11]。針對矩形鋼管節點軸向剛度的理論研究，國外常用的方法是構件法，該方法通過將節點傳力區域等效成一系列彈簧來計算節點軸向剛度。構件法最早由Zoetemeijer[12]提出，隨后被Weynand等[13]推廣應用于管狀節點，Garifullin等[14]在此基礎上修正主管表面彎曲和主管側板受拉(受壓)2個基本構件，并提出新的計算公式。但在構件法的計算中仍未考慮主管側板的抗彎貢獻，且忽略各個基本構件之間的相互影響。中國對鋼管節點軸向剛度的理論研究多集中于圓形鋼管節點[15-17]，對矩形鋼管節點研究較少，武振宇等[18]根據塑性鉸線模型提出矩形鋼管節點軸向剛度公式，但是公式復雜且不易于推廣應用。目前國內外針對矩形鋼管混凝土節點軸向剛度的理論研究均較少，劉永健等[19-20]對T形節點受拉力學行為進行分析并提出抗拉剛度簡化計算模型，但對簡化計算模型沒有進行深入分析，未提出相關計算公式。綜上所述，矩形鋼管和鋼管混凝土節點軸向剛度的研究均較少，針對矩形鋼管節點，構件法未考慮主管側板的影響；針對矩形鋼管混凝土節點，缺乏相應的節點軸向剛度計算公式。

平面桁架常見的節點類型主要有T，Y，K，N形節點，在軸向荷載作用下，當K，N形節點2個支管相距較遠時，可忽略2個支管的相互作用，等效成Y形節點或T形節點進行計算；當Y形節點支管和主管垂直時即為T形節點，因此T形節點為分析其他節點類型的基礎。同時，當支主管寬度比β較小時，節點變形較大，受力更為不利。為此，本文選取T形不等寬節點(β≤0.8)，根據其受力特點，建立了矩形鋼管節點和鋼管混凝土節點軸向剛度的簡化力學模型，在此基礎上推導了2類節點軸向剛度的理論公式，通過有限元方法回歸擬合得到節點域有效長度leff計算公式，通過將節點軸向剛度理論公式計算結果與試驗及有限元結果進行對比，驗證了2類節點軸向剛度公式的可靠性。

1 節點變形及軸向剛度簡化模型

1.1 節點變形的定義

節點剛度為節點在外荷載作用下抵抗變形的能力，可定義為外荷載與節點變形的比值，對節點變形的組成進行分析有助于將節點剛度進行拆分。對于簡支桁梁橋，在荷載作用下，節點部位的總變形Δ主要由3個部分組成：弦桿的彎曲變形Δ1、腹桿的軸向拉壓變形Δ2及節點的局部變形Δ3，如圖1所示，其中F為節點受力。總變形Δ可根據式(1)進行計算，其中Δ1和Δ2為桁架的整體變形，可通過結構力學進行求解，Δ3由于節點連接區域的復雜性，難以直接進行求解，因此本文分析的節點變形均指主管的局部變形。

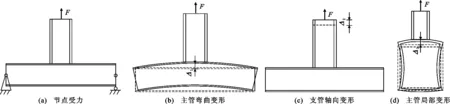
圖1 節點變形示意圖Fig.1 Schematic Diagram of Joints Deformation

(1)

矩形鋼管桁架的節點主要分為受拉節點和受壓節點，對于矩形鋼管節點，其受壓和受拉力學行為相似，均以板件抗彎為主，節點受力模式類似于框架模型受力。在矩形鋼管節點主管中填充混凝土，限制了主管側板的內凹變形及角隅部的轉動，此時節點受力模式已發生改變。相對于矩形鋼管節點，矩形鋼管混凝土節點受拉時，混凝土限制了主管角隅部轉動，從而減小了主管頂板的外凸變形，如圖2所示；矩形鋼管混凝土節點受壓時，混凝土限制了主管頂板的內凹變形，如圖3所示。

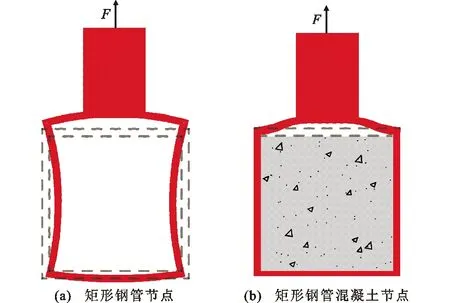
圖2 受拉節點變形對比Fig.2 Deformation Comparison of Tension Joints

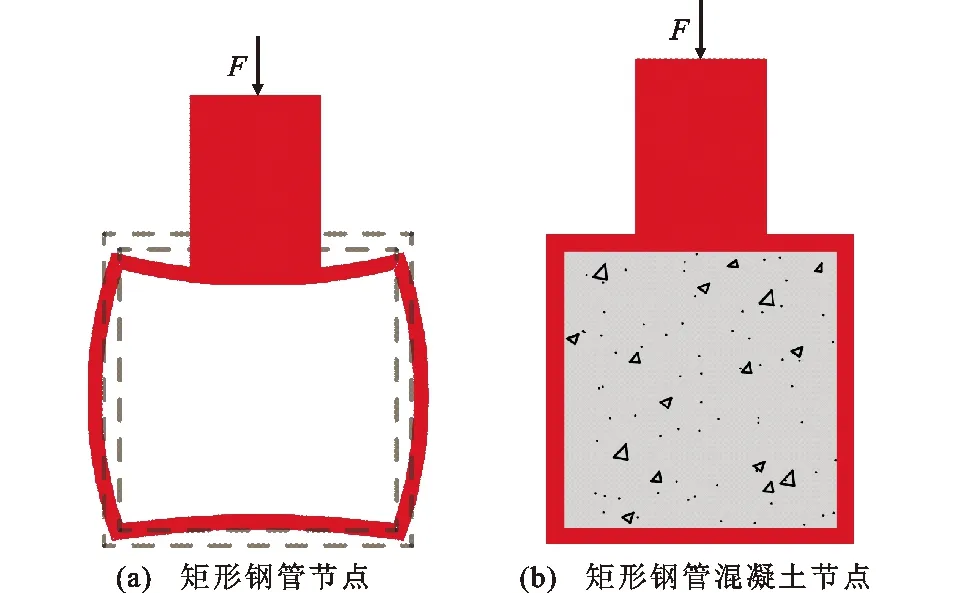
圖3 受壓節點變形對比Fig.3 Deformation Comparison of Compression Joints

1.2 節點軸向剛度簡化模型

節點軸向剛度為支主管連接處的局部剛度，與桁架中的節點變形相對應。為便于工程設計人員的使用，本文提出節點軸向剛度的簡化計算模型。由Wardenier等[21]、侯蓓蓓等[22]的分析可知，荷載從支管傳遞至主管的過程中，支管存在不均勻的應力分布，中部應力低，角隅部應力高，因此可對節點的傳力路徑簡化，認為荷載僅從支管的4個角隅部傳遞至主管表面，如圖4(a)所示；進行節點軸向剛度分析時，根據支管角隅部傳力特性，可將支管4個角隅部等效為4個彈簧進行剛度分析，如圖4(b)所示；節點支主管連接區域采用4個并聯彈簧進行模擬，若將節點的支管和主管看成一個桿件，此時可將支主管連接處看成一個總彈簧(剛度為K)，形成節點軸向剛度最終簡化模型，如圖4(c)所示，K根據式(2)進行計算。一般工程設計人員更多地關注節點彈性階段的力學行為，因此本文分析的節點軸向剛度為彈性初始剛度。

K=4keq

(2)

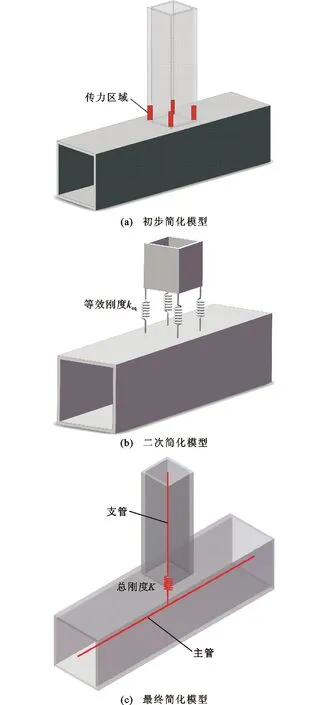
圖4 節點軸向剛度模型簡化過程Fig.4 Simplification Process of Joint Axial Stiffness Model

2 矩形鋼管節點軸向剛度的理論推導

2.1 節點軸向剛度理論推導

對于矩形鋼管不等寬受拉節點(β≤0.8)，節點變形以主管板件的彎曲變形為主。節點受力模式類似于框架受力，沿節點縱向主管并非完全參與受力，而是存在有效部分，稱為節點域有效長度leff。進行框架分析時，由于主管以板件彎曲變形為主，支主管連接部位不均勻，局部變形較小，可將支主管連接區域簡化為剛性體，如圖5(a)所示，其中b0為主管寬度，h0為主管高度，t0為主管厚度，b1為支管寬度，h1為支管高度，t1為支管厚度。節點軸向剛度模型為空間模型，通過leff簡化為平面框架模型，框架模型寬度為b0-t0，高度為h0；橫截面寬度為leff，高度為t0，如圖5(b)所示。

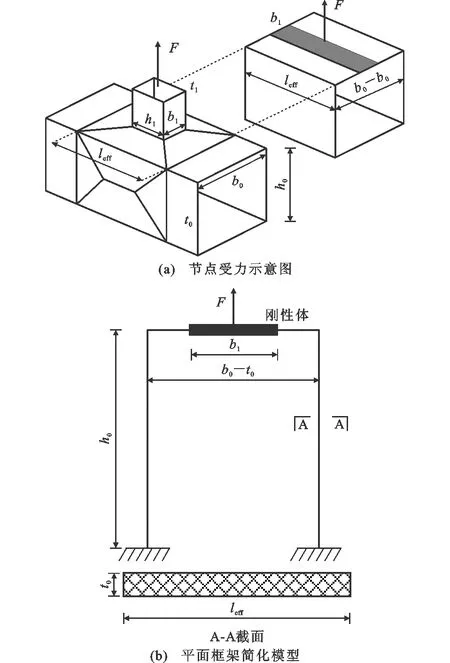
圖5 矩形鋼管節點力學模型示意圖Fig.5 Schematic Diagram of RHS Joint Mechanics Model

平面框架模型為對稱結構，為簡化計算，取一半結構進行結構分析，如圖6所示，采用力法對超靜定結構進行求解，力法的基本方程如式(3)所示。

(3)

式中：X1，X2為多余約束力；δ11，δ21分別為基本結構在X1=1單獨作用下沿X1，X2方向的位移；δ12，δ22分別為基本結構在X2=1單獨作用下沿X1，X2方向的位移；Δ1P，Δ2P為基本結構在荷載單獨作用下沿X1，X2方向的位移。

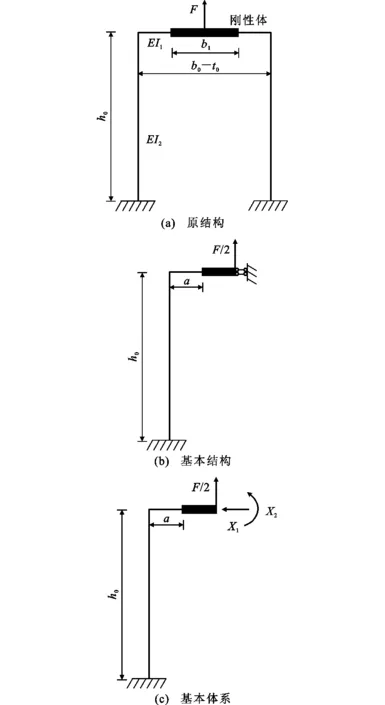
圖6 矩形鋼管節點結構分析圖Fig.6 Structural Analysis Diagram of RHS Joint

求解得多余約束力X1和X2，如式(4)，(5)所示。

(4)

(5)

根據圖解法，求解框架模型加載點位置的變形

(6)

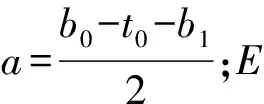
矩形鋼管節點軸向剛度的理論公式為

(7)

假定節點主管頂板和側板節點域有效長度相同，則

(8)

2.2 節點域有效長度的擬合

由節點剛度的分析可知，節點域有效長度leff為節點空間模型簡化為平面框架模型的關鍵參數，也是節點軸向剛度計算公式的唯一未知量，因此本文通過有限元方法分析leff。

2.2.1 有限元模擬方法

桁架中的節點變形僅指主管的局部變形，為此，本文通過在主管底板固接限制主管桿件的彎曲變形，將支管設置為剛性體限制支管桿件的軸向變形，此時在荷載F作用下，加載點的位移Δ即反映主管桿件的局部變形，如圖7所示。

圖7 矩形鋼管節點變形Fig.7 Deformation of RHS Joint

本文采用通用有限元軟件ABAQUS進行建模分析，進行節點軸向初始剛度分析時，鋼材應力處于彈性階段，因此鋼材采用彈性的應力-應變關系，主管彈性模量Es=2.06×105MPa，泊松比νs=0.283，支管為剛性體，彈性模量Es=2.06×108MPa，泊松比νs=0.283；為了避免主管端部邊界條件對節點力學性能的影響，主管長度設置為6b0，支管長度為b1；支管和主管均采用結構化網格劃分技術，網格尺寸為10～20 mm，并保證支管和主管厚度方向至少為2層網格；支管和主管均采用C3D20R二十節點減縮積分六面體單元，支主管連接部位的單元采用共節點方式連接；將支管端部表面耦合到加載點，并施加100 kN的集中荷載，此時加載點的自由度即為支管端面的自由度，主管底板兩側僅限制3個方向的位移(dx=dy=dz=0)而不限制轉動；參考文獻[14]，[16]，[20]可知，焊縫對節點整體力學性能影響較小，因此不考慮焊縫影響。節點有限元模型如圖8所示。

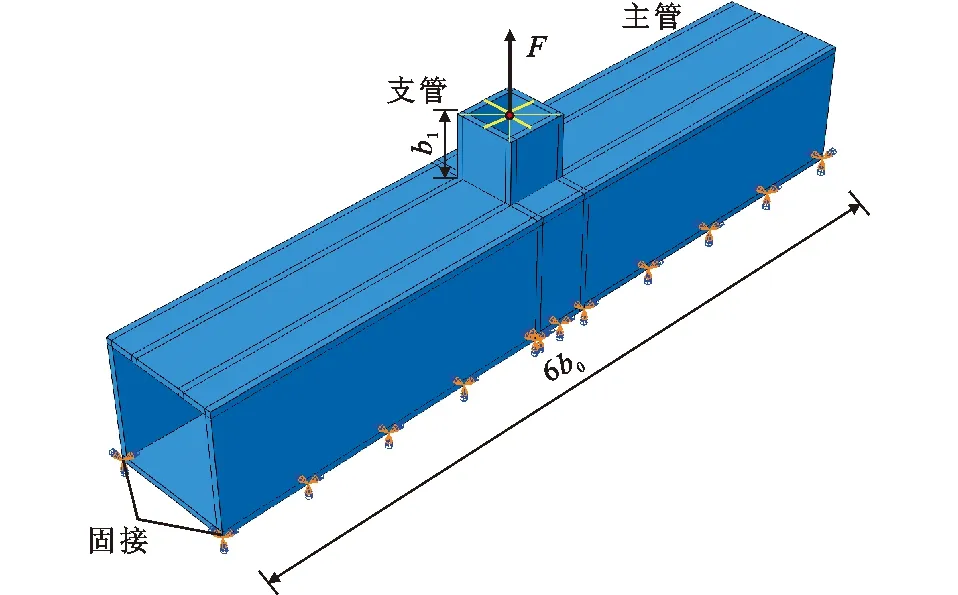
圖8 矩形鋼管節點有限元模型Fig.8 Finite Element Model of RHS Joint

2.2.2 參數取值范圍及公式擬合

有限元模型中節點域有效長度leff可根據公式(8)反算，結果如式(9)所示。

(9)

通過分析可知，leff與節點幾何參數b0，h0，t0，b1，h1有關，國際管結構協會CIDECT規范[2]和《鋼結構設計標準》(GB 50017—2017)均規定節點量綱一參數的取值范圍，為便于分析，將參數化簡成1個幾何參數b0和4個量綱一參數α，2γ，β，η，其中α=h0/b0，為主管高寬比，2γ=b0/t0，為主管寬厚比，β=b1/b0，為支主管寬度比，η=h1/b1，為支管高寬比。根據規范規定確定節點取值范圍，如表1所示。由于節點參數較多，此處考慮設計正交試驗進行初始參數分析。

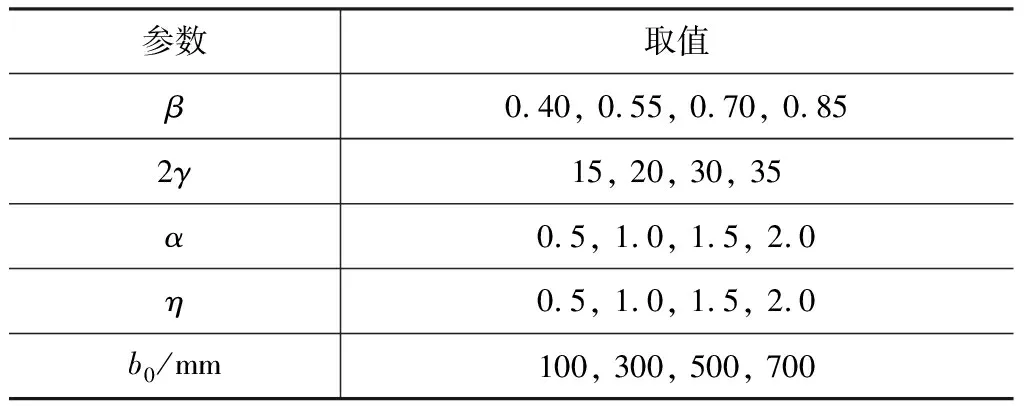
表1 節點參數取值范圍Tab.1 Parameter Value Range of Joint

根據正交試驗設計表L16(45)對節點參數進行正交試驗設計，對正交試驗結果進行極差分析確定各個因素對leff影響程度的大小，結果如圖9所示。由圖9可知，leff與b0，η呈線性關系，與β，α，2γ呈非線性關系，在規范規定范圍內，b0，η，β，α，2γ對leff的影響從大到小依次為450，323，320，112，28 mm。占leff最大值的百分比分別為88%，72%，78%，32%，9%，如圖10所示。因此，忽略α，2γ，僅考慮b0，η，β對leff的影響，并結合桁架實際節點尺寸進行全參數分析，共建立80個參數模型，參數的取值范圍如表2所示。

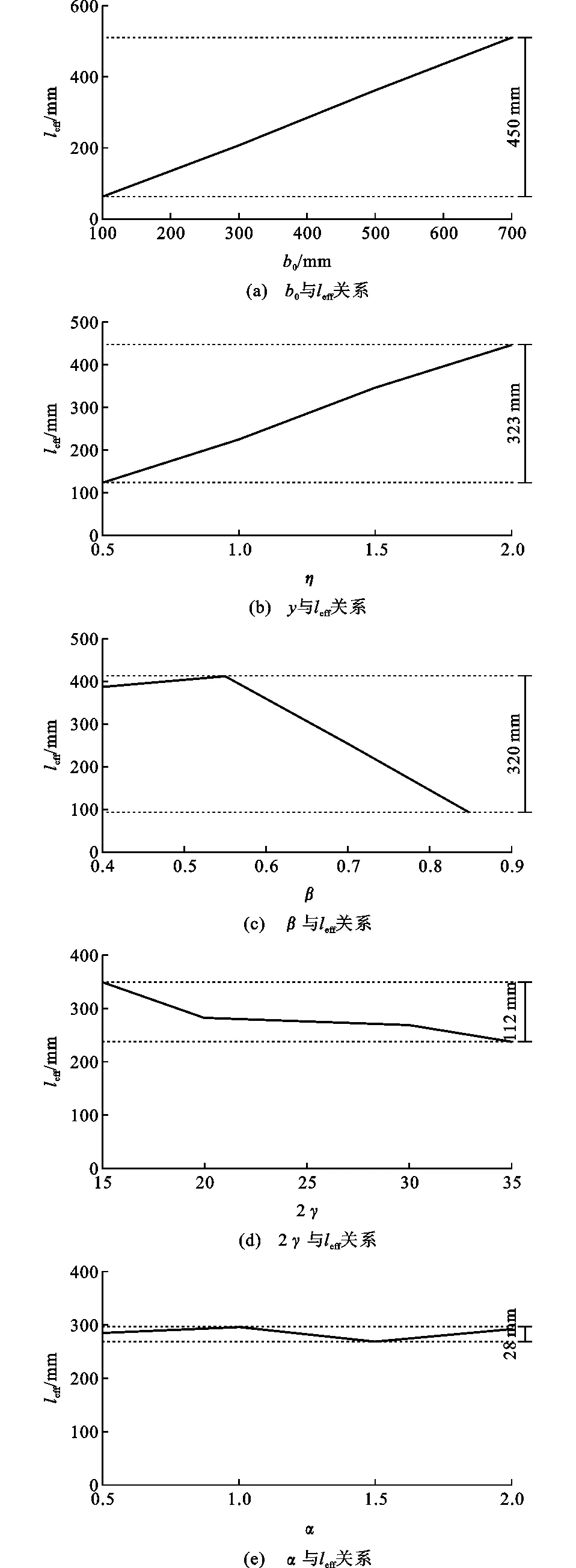
圖9 節點域有效長度leff單因素分析結果Fig.9 Single Factor Analysis Results of Joint Domain Effective Length leff

圖10 單因素顯著性水平分析結果Fig.10 Significance Level Analysis Results of Single Factor

采用公式(9)計算有限元模型中的leff，結果如圖11所示。由圖11(a)，(b)可知，leff與b0和η均呈線性關系，且隨之增大而增大；由圖11(c)可知，leff與β呈非線性關系，且隨之增大而減小。圖11(a)中的直線接近于等間距直線，可認為因素b0和η互不影響，不存在耦合作用，圖11(b)，(c)中均為不等間距的直線或曲線，可認為因素b0，η和β存在耦合作用。

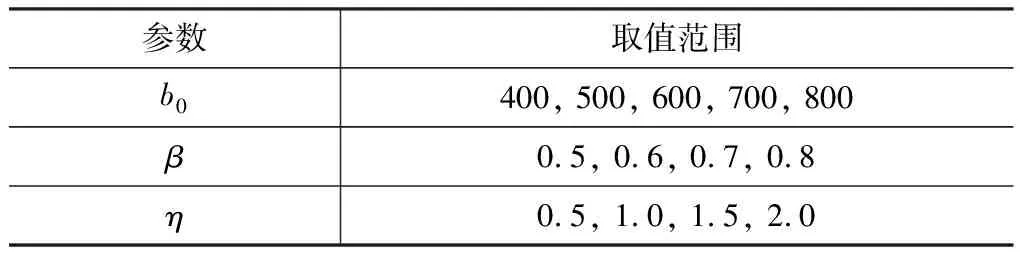
表2 節點最終參數取值范圍Tab.2 Final Parameter Value Range of Joint

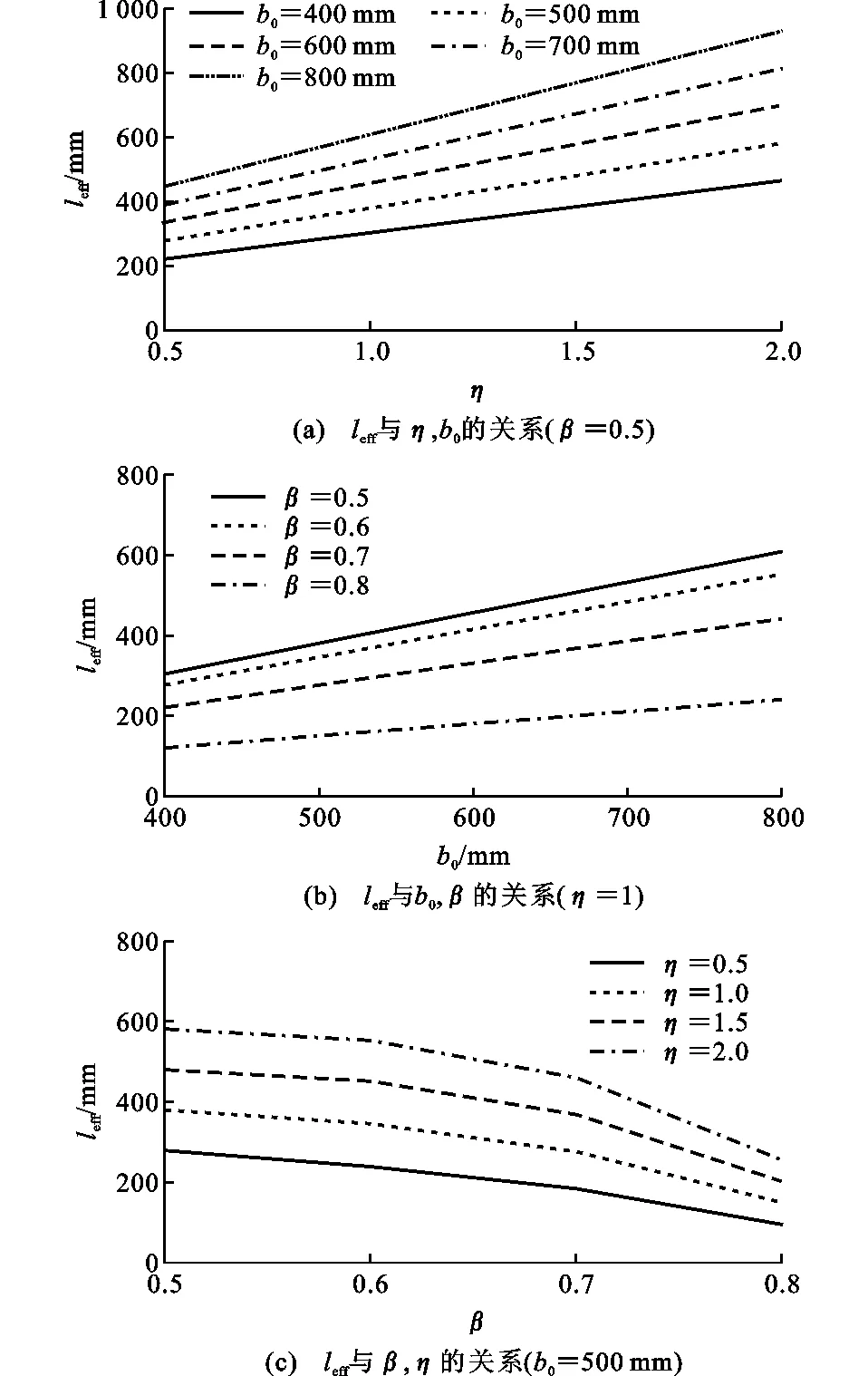
圖11 矩形鋼管節點域有效長度leff參數分析結果Fig.11 Parameter Analysis Results of RHS Joint Domain Effective Length leff

基于以上分析，擬合得到leff的計算公式為

leff=b0(0.65-0.65β)+h1(1.98-2.17β)

(10)

擬合公式計算結果和有限元計算結果對比如圖12所示，擬合公式的判定系數R2=0.987，說明該公式擬合良好。

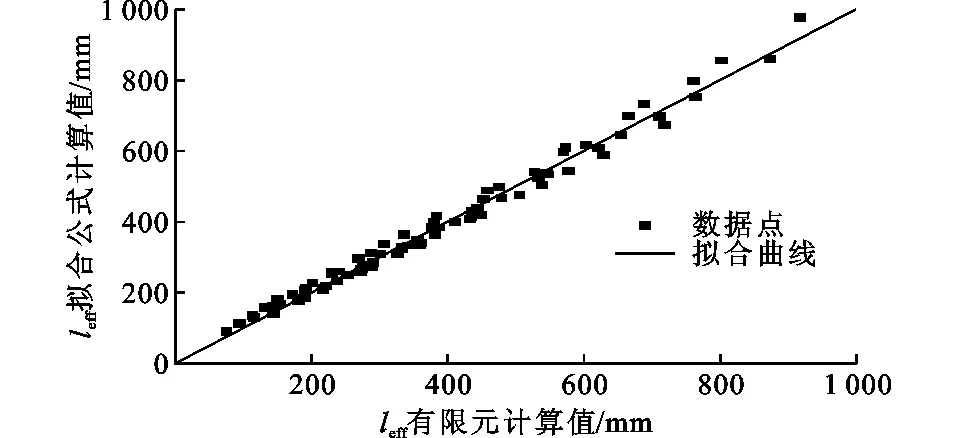
圖12 矩形鋼管節點擬合公式和有限元結果對比Fig.12 Comparison of Fitting Formula and Finite Element Results of RHS Joint

3 矩形鋼管混凝土節點軸向剛度的理論推導

3.1 節點剛度公式理論推導

相對于矩形鋼管節點，矩形鋼管混凝土節點內填混凝土限制了主管角隅部的轉動，節點受力模式類似于固端梁受力(圖13)。與矩形鋼管節點相同，矩形鋼管混凝土節點也存在節點域有效長度leff。

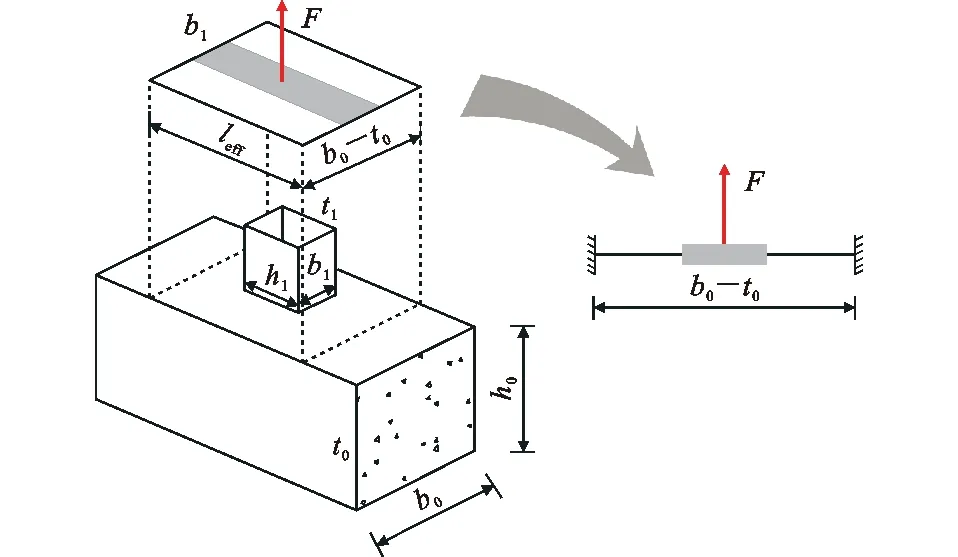
圖13 矩形鋼管混凝土節點力學模型示意圖Fig.13 Schematic Diagram of CFRHS Joint Mechanics Model

矩形鋼管混凝土節點軸向剛度簡化計算模型為固端梁模型，可根據位移法求得基本結構彎矩圖，結合圖解法求得節點變形，結構分析如圖14所示。節點變形通過式(11)計算。

(11)

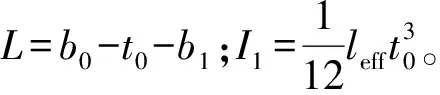
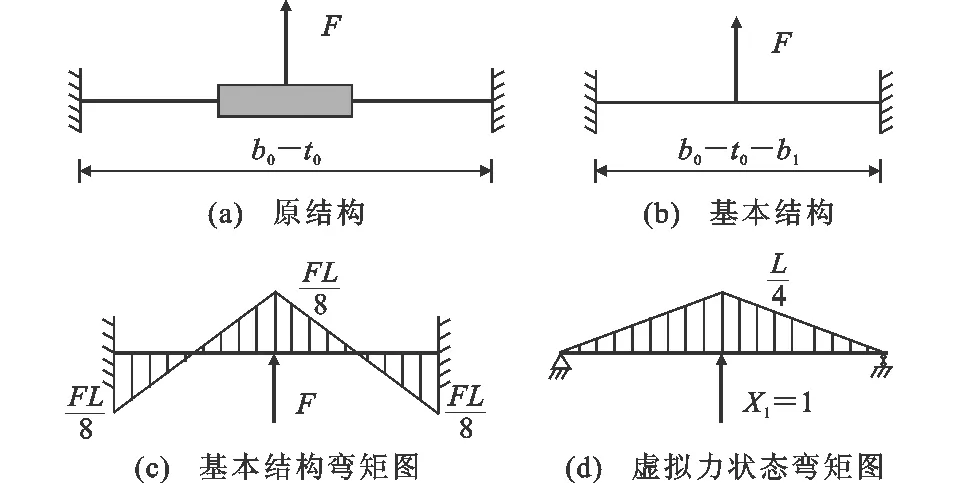
圖14 矩形鋼管混凝土節點結構分析圖Fig.14 Structural Analysis Diagram of CFRHS Joint

矩形鋼管混凝土節點的軸向剛度理論公式為

(12)

3.2 節點域有效長度擬合

3.2.1 有限元建模方法介紹

與矩形鋼管節點相同，矩形鋼管混凝土節點也采用有限元方法計算節點域有效長度leff。在矩形鋼管節點建模方法的基礎上，對主管內填充混凝土。進行節點軸向初始剛度分析時，混凝土不發生開裂，因此混凝土采用彈性應力-應變關系，混凝土彈性模量根據《混凝土結構設計規范》(GB 50010—2010)中混凝土強度等級進行取值，泊松比νs=0.167；混凝土采用結構化網格劃分技術，采用C3D8R八節點減縮積分的六面體單元進行模擬，混凝土長度與主管長度一致，為6b0；混凝土和鋼管之間的界面接觸模型采用“硬接觸”模擬法向行為，兩者不能相互侵入，并選取剛度較大的混凝土為主面，鋼管為從面，采用庫倫摩擦模擬切向行為，摩擦因數取0.3[23-24]。矩形鋼管混凝土節點有限元模型如圖15所示，荷載作用下的節點變形如圖16所示。

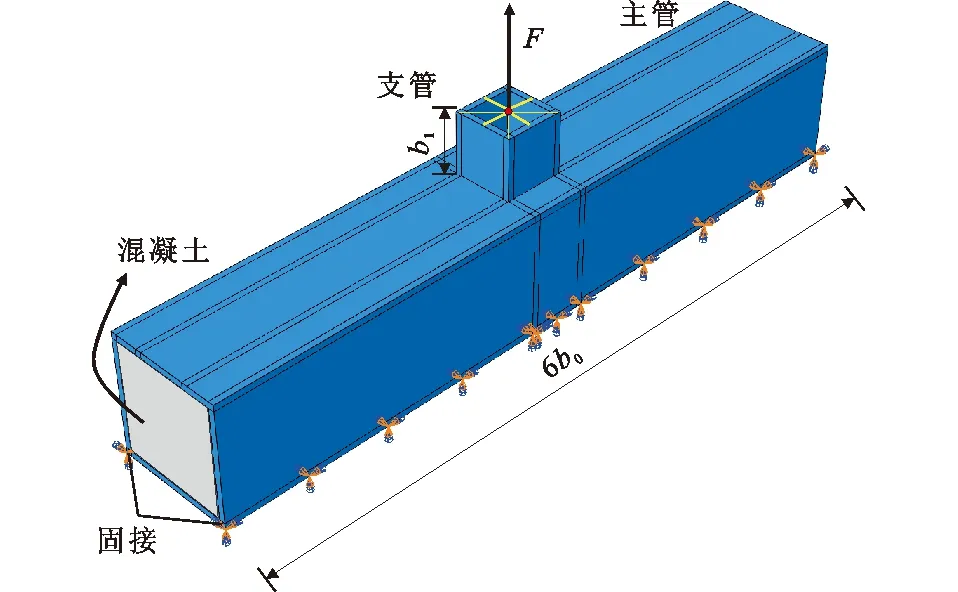
圖15 矩形鋼管混凝土節點有限元模型Fig.15 Finite Element Model of CFRHS Joint

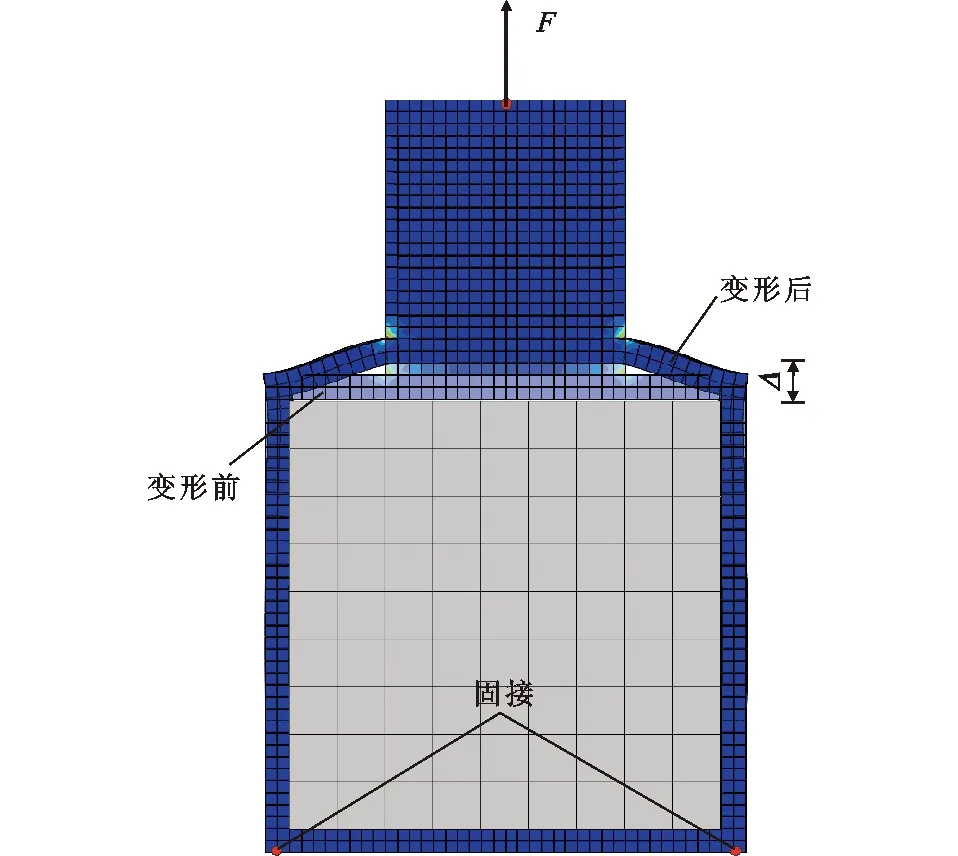
圖16 矩形鋼管混凝土節點變形Fig.16 Deformation of CFRHS Joint

3.2.2 參數取值范圍及公式擬合

有限元模型中leff可根據公式(12)反算，結果如式(13)所示。

(13)

矩形鋼管混凝土節點參數取值范圍與鋼管節點相同，見表2。節點域有效長度leff與各參數的影響規律如圖17所示。由圖17可知：leff與b0和η均呈線性關系，且隨之增大而增大；leff與β呈非線性關系，且隨之增大而減小，影響規律與矩形鋼管節點相似。

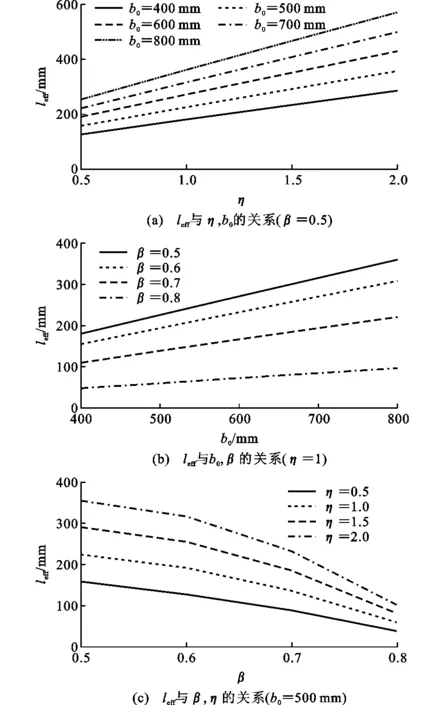
圖17 矩形鋼管混凝土節點域有效長度leff參數分析結果Fig.17 Parameter Analysis Results of Joint Domain Effective Length leff of CFRHS

基于以上分析，擬合得到leff的計算公式為

leff=b0(0.4-0.44β)+h1(1.31-1.5β)

(14)

擬合公式計算結果和有限元計算結果的對比如圖18所示，擬合公式的判定系數R2=0.998，說明該公式擬合良好。

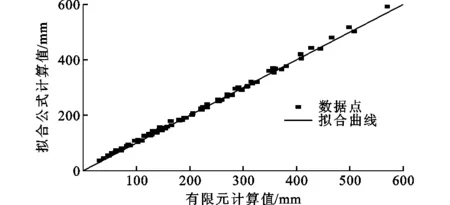
圖18 矩形鋼管混凝土擬合公式和有限元結果對比Fig.18 Comparison of Fitting Formula and Finite Element Results of CFRHS

4 理論公式與試驗及有限元結果的對比

4.1 試驗結果的獲取

國內外針對矩形鋼管節點和鋼管混凝土節點軸向剛度的試驗研究均未見相關報道，大部分都是針對節點承載力的試驗研究[19,25-30]。在軸向荷載作用下，節點受力過程如圖19所示(其中，ki為彈性階段初始剛度，kh為強化階段硬化剛度)，受力過程可分為4個節段：彈性階段、彈塑性階段、強化階段、破壞階段，Packer等[31]將彈性階段初始剛度和強化階段硬化剛度的交點作為節點設計承載力(Fd)。本文在此基礎上，將節點承載力試驗中荷載-位移曲線彈性階段的初始剛度作為節點軸向剛度。由于初始剛度的人為因素較大，為減小初始剛度取值的隨機性，結合Zhao[32]對節點變形極限的分析，取主管表面變形達到0.5%b0時的割線剛度作為軸向初始剛度試驗值，割線剛度通過F0.5%b0/Δ0.5%b0計算得到，其中，Δ0.5%b0代表主管表面變形達到0.5%b0，F0.5%b0為Δ0.5%b0對應的荷載，如圖20所示。

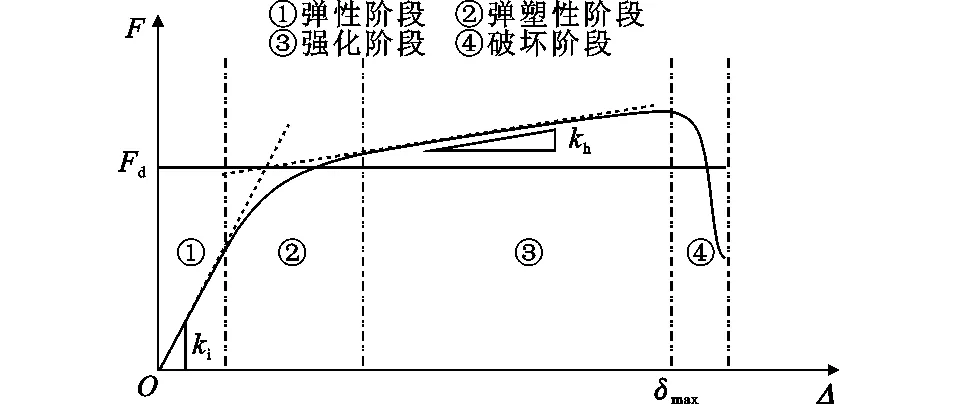
圖19 節點受力全過程曲線Fig.19 Whole Process Curve of Joint Stress

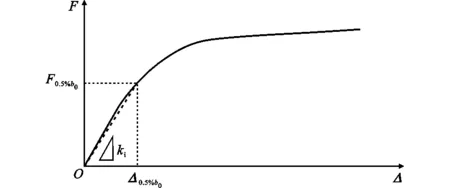
圖20 軸向初始剛度的作圖法Fig.20 Graphical Approach for Initial Axial Stiffness

4.2 理論公式與試驗結果的對比

本文基于框架模型提出了矩形鋼管T形受拉節點軸向剛度計算公式，基于固端梁模型提出了矩形鋼管混凝土T形受拉節點軸向剛度計算公式，為驗證節點軸向剛度理論公式的準確性，將現有研究中T形節點承載力試驗進行整理，提取節點荷載-位移曲線中彈性初始剛度，并與軸向剛度理論公式進行對比，如表3所示。Garifullin等[14]指出，節點軸向初始剛度無須像承載力精確度那么高，在工程設計上允許有30%的偏差，總體上，本文理論公式計算結果與試驗結果吻合較好，而對于矩形鋼管混凝土節點，由于試驗數據較少，仍需更多的試驗數據驗證公式的準確性。

4.3 理論公式與有限元結果的對比

由于試驗裝置偏心、試件加工誤差和焊縫等原因，節點承載力試驗初始剛度可能與真實節點軸向剛度存在一定的差異，為此，本文進行理論公式與有限元結果的對比，有限元參數取值范圍見表2，結果如圖21，22所示。矩形鋼管節點和鋼管混凝土節點理論公式結果與有限元結果吻合較好，2類節點理論公式與有限元結果比值的均值分別為1.010和1.034，變異系數分別為0.005和0.003，差值基本在15%以內。

5 節點軸向初始剛度分析

將矩形鋼管和鋼管混凝土節點的軸向剛度進行對比，得到混凝土提高系數kc/h，kc/h通過式(15)進行計算。

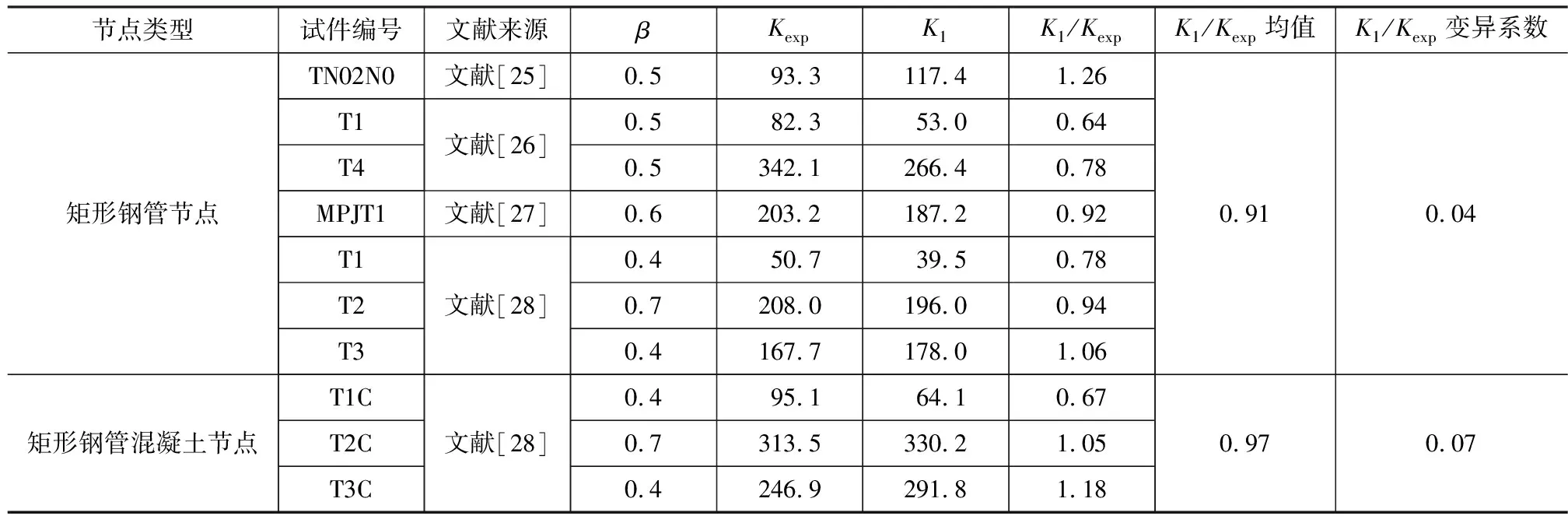
表3 節點軸向剛度理論公式與試驗結果對比Tab.3 Comparison of Theoretical Formula and Experimental Results of Joint Axial Stiffness

注：Kexp為節點軸向剛度試驗值；K1為本文剛度公式計算值。

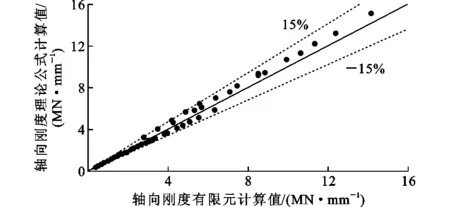
圖21 矩形鋼管節點軸向剛度理論公式與有限元結果對比Fig.21 Axial Stiffness Comparison of Theoretical Formula and Finite Element Results for RHS Joint

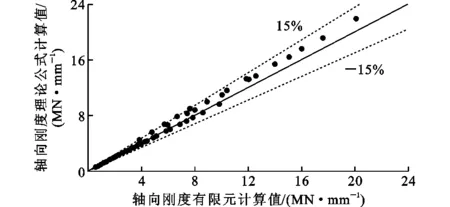
圖22 矩形鋼管混凝土節點軸向剛度理論公式與有限元結果對比Fig.22 Axial Stiffness Comparison of Theoretical Formula and Finite Element Results for CFRHS Joint

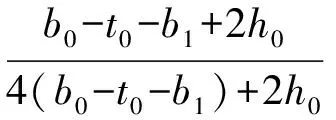
(15)

由于上述公式較為復雜，為便于工程應用，對公式進行量綱一化分析，并將公式進行必要的簡化，假設桁架節點的支管為方形鋼管(h1=b1)，此時kc/h只與α，β有關，計算公式如式(16)所示。

(16)

kc/h與α，β變化規律如圖23所示，由圖23可知：kc/h隨著α的增大而增大，產生這種現象的原因是矩形鋼管混凝土節點計算模型為固端梁模型，α的影響較小，矩形鋼管節點為框架模型，主管側板長度隨著α的增大逐漸增加，框架逐漸變柔，框架模型逐漸向簡支梁模型過渡，矩形鋼管節點軸向剛度逐漸降低；kc/h隨著β的增大呈現先增大后減小的規律，發生上述規律的原因是當β較小時，混凝土對節點外凸變形的約束較明顯，此時隨著β的增加，kc/h逐漸增大，當β增大到某一程度時，隨著β的增加，矩形鋼管節點受力模式逐漸由框架抗彎向主管側板抗拉轉化，混凝土的約束作用減弱，kc/h逐漸減小。當β=0.6～0.7時，混凝土對節點軸向剛度的提高作用最顯著。

圖23 kc/h與α，β的關系Fig.23 Relationship of kc/h, α，β

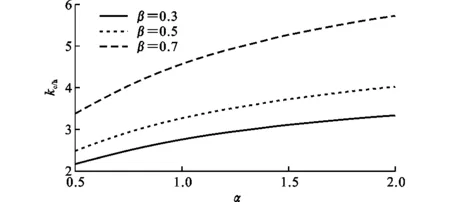
圖24 文獻[19]中kc/h與α,β的關系Fig.24 Relationship of kc/h, α, β in Reference[19]

文獻[19]中對X形節點的kc/h進行了分析討論，節點簡化模型橫截面寬度取單位寬度，結果如圖24所示。由圖24可知，文獻[19]中混凝土提高范圍在2倍～6倍，本文中kc/h提高范圍在1倍～1.8倍，相對于本文計算結果，文獻[19]中的計算結果過于樂觀，但α，β對kc/h的影響規律與本文結論一致。

6 結語

(1)基于T形節點受力特點，提出適用于矩形鋼管節點的框架計算模型和矩形鋼管混凝土節點的固端梁計算模型，并運用力法和位移法推導得到2類節點的軸向剛度理論公式。

(2)采用有限元方法計算節點域有效長度leff，忽略次要影響因素α，2γ的影響，對b0，η，β進行擬合，得到leff計算公式。2類節點leff的變化規律相似，均與b0和η呈線性關系，且隨之增大而增大，與β呈非線性關系，且隨之增大而減小。

(3)基于節點域有效長度leff公式，得到節點軸向剛度公式，取變形為0.5%b0時的割線剛度作為節點荷載-位移曲線軸向剛度的試驗值，通過節點軸向剛度理論公式計算結果與試驗和有限元結果的對比，驗證了節點軸向剛度理論公式的準確性。

(4)將矩形鋼管節點和鋼管混凝土節點軸向剛度進行對比，結果表明主管內填混凝土可以提高節點軸向剛度，并且kc/h隨著α增大而增大，隨著β的增大呈現先增大后減小的規律，且當β=0.6～0.7時提高最大。