基于機器視覺的微型擺輪質量檢測系統①

魏東亮,周迪斌,張家瑜,馬建峰

1(杭州師范大學 杭州國際服務工程學院,杭州 311121)

2(杭州手表有限公司,杭州 310015)

在精密機械行業,微型擺輪(圖1)是一種常見的部件,在生產過程中容易出現表面不平整,邊緣處弧度不達標等缺陷.因此,在組裝設備之前必須進行嚴格檢測,剔除次品.傳統的檢測方法主要是人工檢測,工人通過雙目顯微鏡放大零件圖像,并手動吹氣來轉動零件,肉眼觀察零件上下擺動幅度,以確定零件是否合格.人工檢測依賴個人經驗,主觀性強,且易疲勞,導致產品質量管理的不穩定,難以量化評估.采用視覺技術進行檢測是大勢所趨,其能有效保證產品檢測的準確度和穩定性.

一個優質的機器視覺系統必須具備以下幾點:第一,所采用的光學系統必須成像清晰,對比度好,噪聲少;第二,算法必須精確的計算出零件的邊緣線;第三,算法必須具有一定的魯棒性,比如能夠自動矯正傾斜的圖像.

圖1 擺輪

數字圖像的基本單位是像素.為了提高檢測的精度,需要進行亞像素的定位.亞像素邊緣檢測是指將邊緣附近的像素進行分解,從而精確定位邊緣[1].常用的亞像素檢測技術有矩法,最小二乘方差法,插值法,擬合法等[2,3].文獻[2,4–6]提出了基于二次曲線擬合的亞像素定位模型,該模型在理想條件下定位精準度高.文獻[7]提出了對二次多項式的最小二乘擬合求梯度的亞像素插值算法,但模型比較復雜,求解速度慢.本文參考了以上文獻中的理論,使用一種基于局部區域特征的二次曲線模型來計算亞像素位置,這種模型考慮了局部的特征和邊緣梯度,精確度高,速度快,能夠滿足項目的需要.

1 項目總體設計

1.1 光學方案設計

由于零件本身微小,且檢測的是輪面的平整度,同時為了減少虛影提高圖像對比度,所以選擇平行背光源.鏡頭選擇高分辨低畸變的遠心鏡頭.

系統采用視頻檢測方式,零件放置在專用的工作臺上,使用導氣管吹動零件轉動.工作臺如圖2所示.

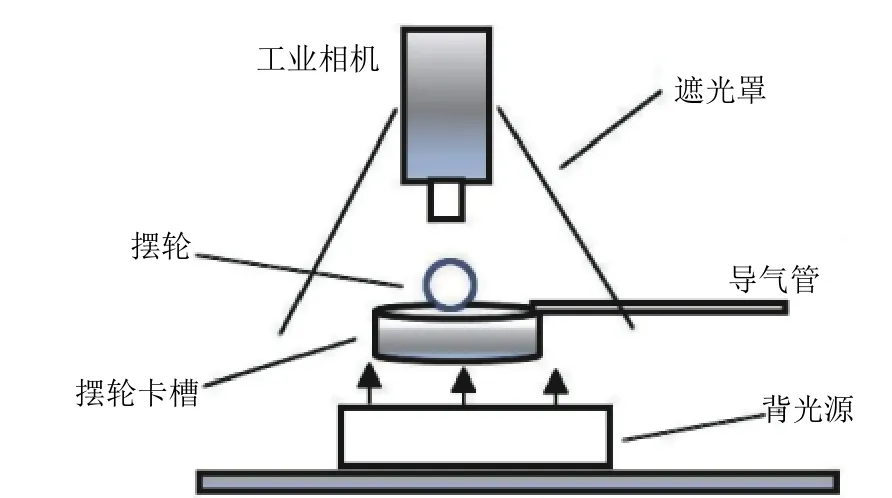
圖2 擺輪工作臺

1.2 算法框架

擺輪檢測依次經歷如下步驟:圖像采集與預處理,Canny邊緣檢測,傾角矯正,ROI (感興趣區域)亞像素位置計算,ROI水平邊緣和垂直邊緣計算,計算極差,判定結果.圖3顯示了這個流程框架.

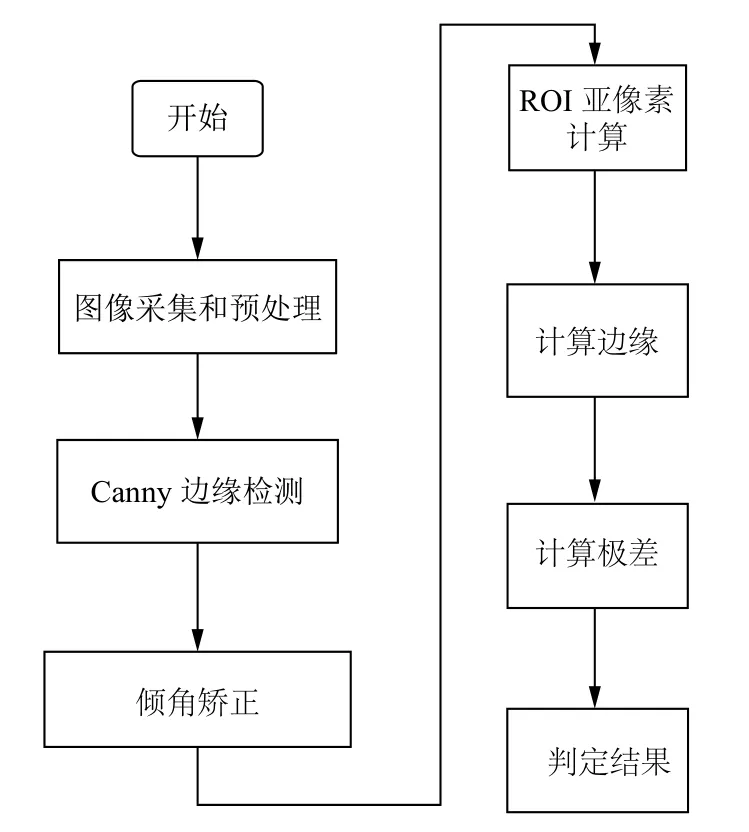
圖3 流程框架

2 算法分析

2.1 圖像采集和預處理

圖像采集是將傳感器檢測到的圖像信息傳輸到計算機的過程.擺輪圖像中背景為白色,目標為黑色,目標和背景的對比度明顯,使用常見幾種閾值分割方法進行實驗,實驗結果如圖4所示.

圖4 常見閾值方法分割效果

從上面的實驗結果來看,OTSU方法,迭代閾值法,p參數法效果都不錯.p參數法依賴于參數的設置,固定的參數會使得算法的魯棒性降低.OTSU在細節體現上比迭代閾值法更好一些,故選擇OTSU法.

2.2 Canny邊緣檢測

圖像的邊緣檢測算法有很多,常見的有Robert,Sobel,Prewitt,Krisch,LOG,Canny等算子[8].使用Canny算子檢測的效果如圖5所示.

圖5 Canny邊緣檢測效果

Canny算法能夠滿足項目需要,且使得后面霍夫直線檢測時取得比較好的性能,所以選擇Canny算子.

2.3 圖像矯正

零件在拍攝的過程中容易存在一定的傾斜,根據先驗知識,傾斜的角度一般在30度以內.目前常用的傾角矯正方法有:基于投影的方法、基于Hough變換、基于線性擬合等方法[9].使用霍夫變換的方法能夠矯正擺輪圖像的傾斜,滿足項目的需求.下面是常見的兩類傾斜情況及其矯正結果,如圖6所示.

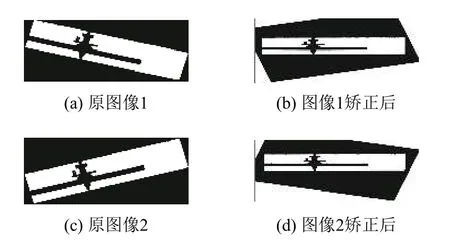
圖6 圖像矯正效果

從上面的實驗結果可以看到,利用霍夫直線檢測算法能夠矯正常見的沿順時針或逆時針具有一定傾斜角度的圖像.

2.3.1 圖像矯正流程

1)基于Canny檢測后的圖像使用霍夫變換方法檢測圖像中的直線.霍夫變換本身比較耗時,但根據擺輪圖像的特點只需要檢測出2到3條比較長的水平直線,其余水平直線和垂直直線則全部忽略掉.當設置直線檢測閾值為500像素點時即可達成上述目標.這樣能大大提高霍夫算法的效率.

2)對于每條檢測出的直線,獲取其傾角θ,如圖7所示.

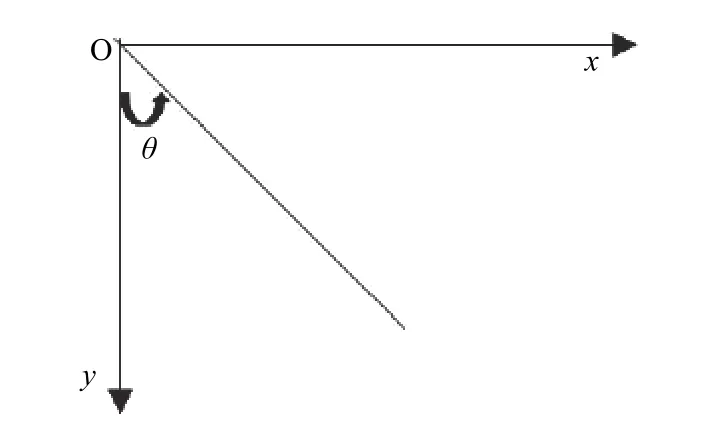
圖7 圖像坐標系

3)旋轉圖像至水平位置.設β為圖像需要旋轉的角度,則有:

圖像旋轉的步驟如下:

第1步,把圖像坐標系的原點從左上角轉移到圖像中心.

第2步,旋轉所有像素點.

第3步,把旋轉后的圖像平移到原來的圖像坐標系中.

2.4 ROI亞像素計算

在該項目中我們使用了5×3的模板,考慮每個可能的邊緣像素,然后在模板區域內計算一個二次曲線模型,利用此模型計算亞像素位置.二次函數模型是在一次函數模型的基礎上推導出來的,所以先介紹一次函數模型.

2.4.1 一次函數模型

如圖8所示,假設直線L:y=kx+b是圖像中的邊緣,且L將圖像區域分成上下兩部分,分別記做M,N.這兩部分的面積記做SM,SN,M,N也表示M,N兩部分的平均灰度值.直線L所在的坐標系的中心點為(i,j).設 (i,j)處 像素的灰度值為F(i,j),它也代表整個模板區域的平均灰度值.設圖像區域總面積為S[2,5].則有:

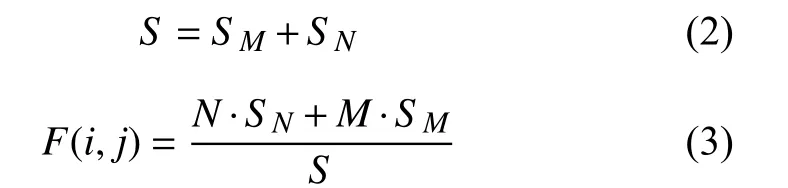
圖8 一次函數模型

我們考慮中間像素 (i,j)的5×3鄰域模板,以L2、M2和R2來表示模板中直線L下側左、中、右列的像素面積,如圖9所示.直線L坐標系中心的位置依然是O(i,j),l列中心的橫坐標是i–1,r列中心的橫坐標是i+1;最上一行的中心縱坐標是j+2,最下一行中心位置的縱坐標是j–2;設每個像素格的邊長為w[2,5].

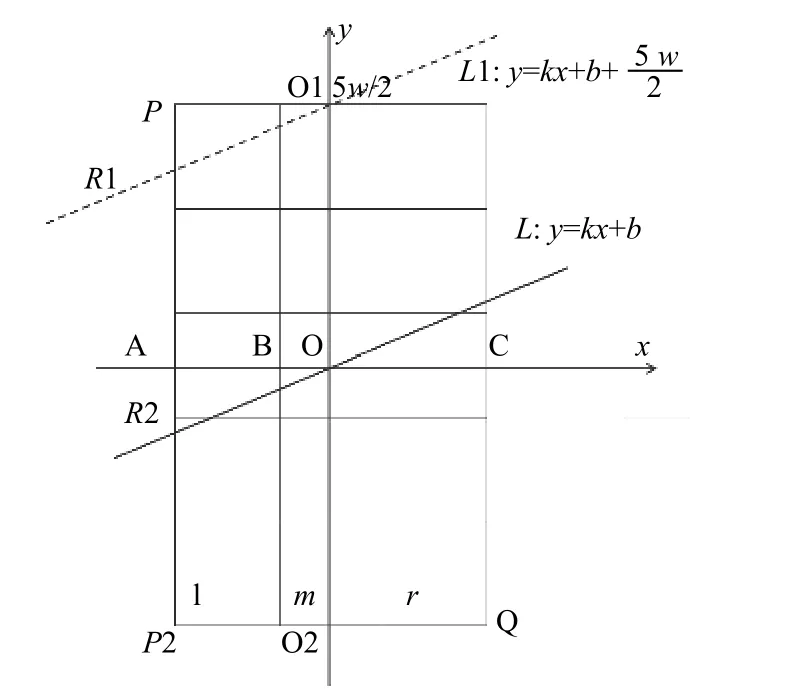
圖9 5×3模板

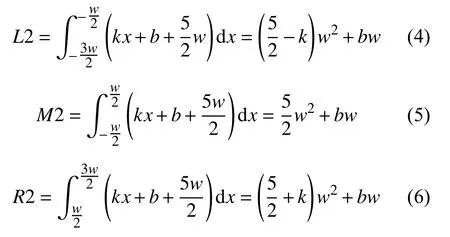
設5×3模板中左邊一列的像素灰度值之和為Tl,中間一列為Tm,右邊一列為Tr,則有:

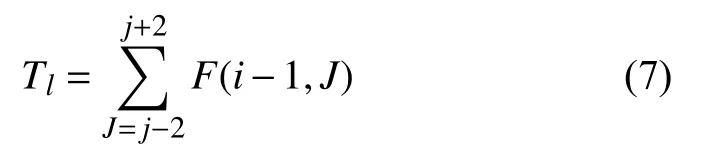
代入式(3),可得:

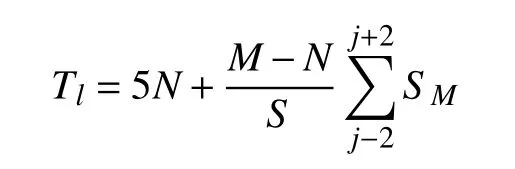
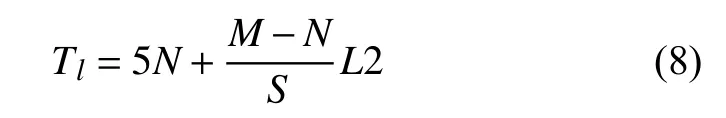
同理,可知:

2.4.2 二次函數模型

一次函數可以看做是二次函數當二次項系數為0時的特例,所以使用二次函數模型來預測亞像素的位置會比一次函數模型更普遍一些.在二次函數模型中我們還可以求得邊緣的曲率,這樣對邊緣的描述會更準確.二次函數模型預測亞像素位置如圖10所示.各數學符號還保持前面的定義,假設拋物線f:y=ax2+bx+c為圖像中的邊緣.

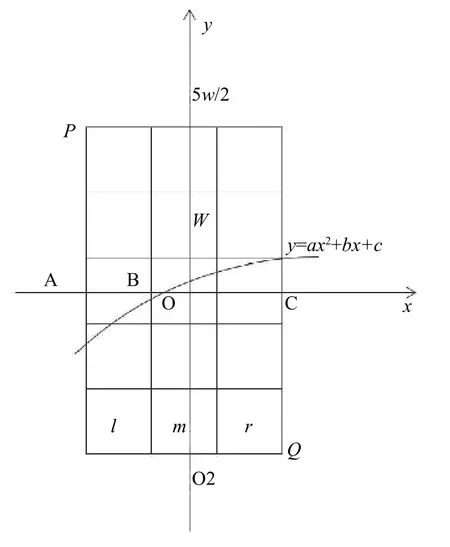
圖10 二次函數模型

邊緣下側左、中、右部分面積計算[2,4–6]:

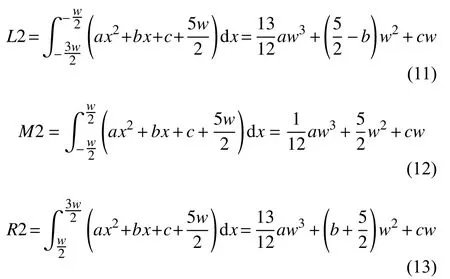
由前面的推導過程可知,式(8),(9),(10)在二次函數模型中依然成立.將式(11),(12),(13)代入式(8),(9),(10)中,可以得到包含了a,b,c三個變量的三個方程,解之,可得a,b,c的值.

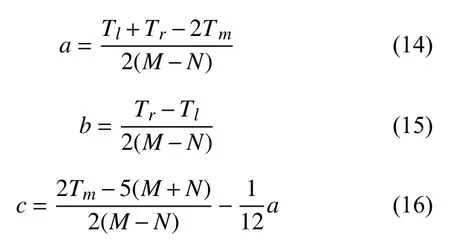
由式(16)可知,二次函數模型下真實的像素點(i,j)對應的亞像素位置為(i,j–c).

在上面的公式中,M,N代表了邊緣兩側平均灰度值,|M–N|則代表了邊緣兩側的梯度幅值,其方向為邊緣的梯度方向.

如圖11所示,設點O(i,j)處沿x方向的偏導數為fx,沿y方向的偏導數為fy,當fx·fy>0 時,設?x=1;當fx·fy≤0 時,?x=?1.

圖11 圖像強度

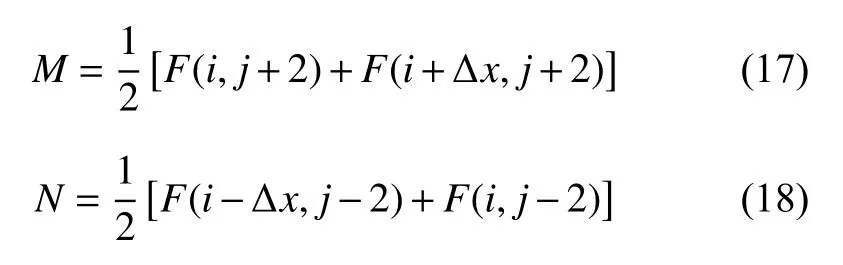
將式(17),式(18)代入前面的公式,即可求得二次函數模型下的亞像素位置.

在使用上述模型之前必須先粗略定位出邊緣的位置.對于每個邊緣點,使用上述模型求解亞像素位置.

2.5 計算邊緣直線

如圖12所示,我們需要描繪出ROI中擺輪邊緣的直線.此處ROI就是方框的區域.可以使用投影法來生成直線.投影法是通過計算圖像在水平和垂直邊緣上的像素點的個數來確定邊緣的位置[10].

圖12 ROI擺輪邊緣直線

計算水平直線的方法如下.ROI中以行為單位,每行的像素數累計起來,相當于往y軸上投影,按照式(19)的方式進行統計.f(i,j)為 (i,j)處的像素值.為了利用計算前面得到的亞像素位置,i,j的增量都設置為0.5像素,即將1個像素點分解為4個亞像素點,這樣就可以將邊緣精確到0.5像素.

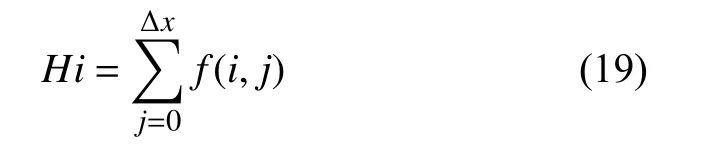
其中,當f(i,j)>100 時,f(i,j)=1 ,當f(i,j)≤100時,f(i,j)=0,Δx是ROI在x軸方向的長度.

在圖12中,從上往下依次是白色區域,黑色區域,白色區域,所以生成的Hi數組從上往下會依次出現峰,谷,峰,取靠上的峰值處的縱坐標y0為生成的水平線段L1的起點P1的縱坐標,L1的終點P2的縱坐標也取y0,P1,P2的橫坐標取ROI的沿x軸方向的起點和終點的橫坐標,連接P1,P2即得到水平線段L1.如圖13所 示.

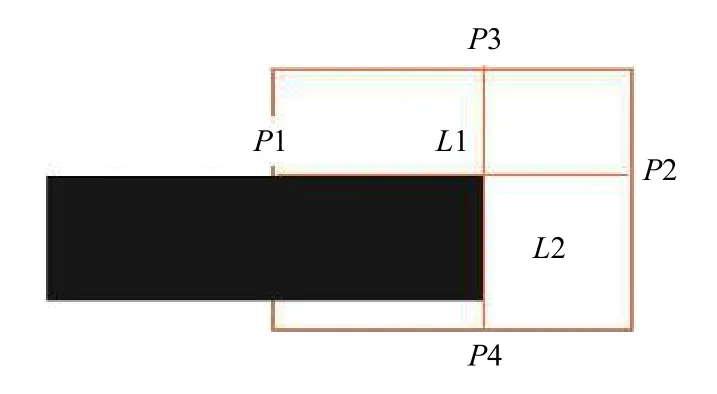
圖13 邊緣直線

生成邊緣垂直線的方法與上面生成水平線的方法類似.只是在計算ROI投影時,以列為單位,統計每列的像素數,相當于往x軸投影,如式(20)所示.

其中,當f(i,j)>100 時,f(i,j)=1 ,當f(i,j)≤100時,f(i,j)=0,Δy是ROI在y軸方向的長度.

在圖12中,從左往右依次是包含黑色區域,純白色區域,所以生成的Vi數組從左往右必然是谷,峰,取峰值處的橫坐標x0為生成的垂直線段L2的起點P3的橫坐標,L2的終點P4的橫坐標也取x0,P3,P4縱坐標取ROI沿y軸方向的起點和終點的縱坐標,連接P3,P4即得到圖13中的垂直線段L2.

2.6 計算極差

視頻檢測時軟件連續的采集幀.對于每一幀,進行上述的處理,生成擺輪的水平邊緣線和垂直邊緣線.擺輪的平面是否平整反映在數據上就是生成的水平線的位置的偏差大小.統計同一個零件的一定數量的幀的水平線位置的極差,依據極差判斷出擺輪表面平整度是否合格.另外,工廠還需檢測擺輪的邊緣處弧度是否標準,這可以通過圖13中一定數量幀的垂直線的極差來判斷.

3 結果分析

按照機械手表行業的規定,2 g微型擺輪產品合格的標準是端跳、徑跳最大偏差都不大于2絲.端跳對應圖13中垂直邊緣,徑跳則對應水平邊緣.系統計量的單位是像素,擺輪的度量單位是絲.

如圖14所示,獲取到擺輪上下邊緣直線的縱坐標y1,y2,經檢測?y=y2?y1=908?814=94像素,已知擺輪設計的厚度為47絲,所以得到下面的換算關系:

圖14 擺輪厚度計算

這樣,在統計動態極差的時候以不大于4像素作為合格的標準.

為了檢測算法的穩定性,對400個擺輪零件進行了測試,其中200個合格品,200個不合格品.對于每一個零件的檢測結果,都與人工檢測結果進行比對.軟件檢測結果如表1所示.

表1 檢測結果

經分析,出錯的原因在于ROI位置設置的有些遠離擺輪末端,重新設置至擺輪末端后,這類誤檢情況沒有再出現.

分析表明,ROI的標記位置是一個影響因素.正確的標記方法是將此區域標記在擺輪的末端,如圖12所示.如果標記在遠離末端位置,零件旋轉時靠中間的位置其擺動幅度較小導致統計的極差較小,這樣可能會導致誤判.檢測系統使用背光源,所以必須在周圍遮光的條件下進行,如果周圍有亮光射入實驗臺就可能干擾實驗結果.

選取有代表性的7個合格品和7個缺陷品,其測試數據見表2.表中偏差值的單位是像素.

表2 對比實驗

系統檢測實況如圖15所示.OK表示合格品,NG表示缺陷品.

系統通過亞像素算法得到的像素點的位置是浮點型數據,根據式(22)將亞像素位置精確到0.5像素的整數倍.

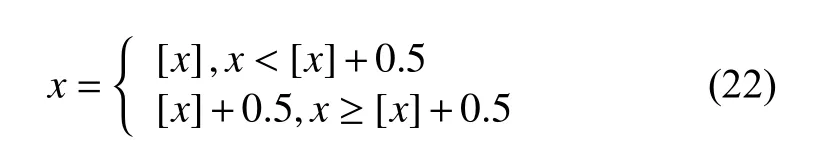
其中,x表示偏差值,x≥0.

表2中,產品序號為2、6、7的零件徑跳最大偏差值都是4像素,屬于合格品.產品序號為12、13的零件徑跳最大偏差為4.5像素,屬于缺陷品.系統在工廠進行了6個月的試運行,具有4、4.5這樣偏差數據的擺輪普遍存在,系統檢測的結論得到了充分的驗證.

由實驗中人工和軟件檢測結論的一致性可以進一步確定,4像素小于等于2絲,4.5像素大于2絲.

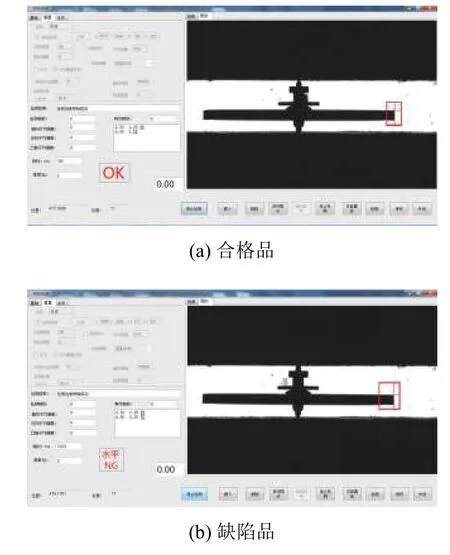
圖15 系統工作實況

由此可知,使用0.5像素代表0.25絲的誤差小于0.03絲.

在上述算法中,亞像素位置的計算對于準確度起著重要作用.項目中偏差值的精確度為0.5像素,在實驗條件下,對應0.25絲的實際長度,這一對應關系誤差小于0.03絲.這能夠滿足工廠對擺輪的檢測要求.

4 結語

目前微型零件檢測技術逐步向非接觸式檢測、數字化檢測等方向發展[11],引入機器視覺檢測技術,既能保證檢測的結果更加精確,可解釋,又能彌補工人數量不足的問題,深受企業的歡迎.本文提出一種微型擺輪的機器視覺檢測算法,算法的平均準確率為99.5%,單幀檢測時間平均27 ms,一個零件可以在2秒鐘之內檢測出結果.實驗結果表明:該算法能夠實時和準確的檢測擺輪的表面平整度和邊緣整齊情況,能夠滿足工業檢測的要求.

目前工廠仍在使用人工上料,如果未來能夠使用精密機械成批的上料,那么整體檢測的效率會更高.