改進回溯搜索優(yōu)化回聲狀態(tài)網(wǎng)絡(luò)時間序列預(yù)測①

胡 率,肖治華,饒 強,廖榮濤

(國網(wǎng)湖北省電力有限公司 信息通信公司,武漢 430077)

現(xiàn)實世界中存在各種各樣的時間序列數(shù)據(jù),分析挖掘數(shù)據(jù)的隱藏信息,基于合理的假設(shè)和推理,建立能夠擬合復(fù)雜系統(tǒng)行為的模型,并依據(jù)該模型對序列未來的發(fā)展規(guī)律做出估計和判斷符合科學(xué)規(guī)律[1].作為時間序列分析的一個研究分支,時間序列預(yù)測在實際中廣泛應(yīng)用.但是,進行時間序列預(yù)測依然存在巨大的挑戰(zhàn),主要原因是時間序列數(shù)據(jù)往往表現(xiàn)出復(fù)雜的特性,比如時序性、高維性、非線性和非周期性等.

人工神經(jīng)網(wǎng)絡(luò)(Artificial Neural Network,ANN)是一種以數(shù)據(jù)為驅(qū)動的、自適應(yīng)的人工智能模型,它具有非常良好的非線性映射能力.從理論角度來講,ANN可以以任意精度無限逼近任何動態(tài)系統(tǒng)的行為[2].ANN幾乎能夠模擬任何線性和非線性的時間序列數(shù)據(jù)生成過程,因而成為準確且應(yīng)用廣泛的預(yù)測模型[3].

2004年,Jaeger等[4]提出了一種全新的遞歸神經(jīng)網(wǎng)絡(luò)——回聲狀態(tài)網(wǎng)絡(luò)(Echo State Network,ESN).ESN最顯著特征是網(wǎng)絡(luò)訓(xùn)練過程簡單:只有儲備池(隱藏層)到輸出層的輸出連接權(quán)值矩陣需要計算,其他各層之間的連接權(quán)值矩陣在網(wǎng)絡(luò)初始化階段隨機生成并保持不變.ESN能夠克服傳統(tǒng)遞歸神經(jīng)網(wǎng)絡(luò)的網(wǎng)絡(luò)結(jié)構(gòu)難以確定、訓(xùn)練效率低下、收斂速度慢、容易陷入局部最優(yōu)等缺點,因而應(yīng)用廣泛.例如網(wǎng)絡(luò)流量預(yù)測[5]、變風(fēng)量空調(diào)內(nèi)模控制[6]和非線性衛(wèi)星信道盲均衡[7]等.標準的ESN在計算輸出連接權(quán)值矩陣時會采用最小二乘估計或者嶺回歸等線性方法,這類方法在節(jié)約計算成本的同時會造成網(wǎng)絡(luò)過擬合.因此,對ESN的輸出連接權(quán)值矩陣進行優(yōu)化以提升其性能具有現(xiàn)實意義.

本質(zhì)上,對ESN的輸出連接權(quán)值矩陣進行優(yōu)化是一個離散、高維和強非線性的復(fù)雜問題.研究指出進化算法(Evolutionary Algorithm,EA)在解決此類問題時性能卓著.宗宸生等[8]運用改進粒子群算法優(yōu)化 BP神經(jīng)網(wǎng)絡(luò)的初始權(quán)重,建立糧食產(chǎn)量預(yù)測模型,該模型具有更高的預(yù)測精度和較大的適應(yīng)度.朱海龍等[9]利用GA優(yōu)化 BP神經(jīng)網(wǎng)絡(luò)的初始權(quán)值和閾值進而建立胎兒體重預(yù)測模型,模型收斂速度和預(yù)測精度都得到提升.針對ESN的優(yōu)化,田中大等[5]利用經(jīng)典的GA對ESN儲備池參數(shù)進行優(yōu)化,進行網(wǎng)絡(luò)流量預(yù)測時獲得不錯的精度.Chouikhi等[10]應(yīng)用PSO對ESN的固定權(quán)值矩陣進行預(yù)訓(xùn)練,以降低連接權(quán)值矩陣在具體應(yīng)用問題上的隨機性.也有學(xué)者使用進化算法對ESN的儲備池到輸出層之間的連接進行優(yōu)化,例如Wang等[11]提出使用BPSO對ESN的儲備池到輸出層之間的連接進行優(yōu)化,優(yōu)化模型在系統(tǒng)識別和時間序列預(yù)測問題上獲得更好的實驗結(jié)果.本文將從提升ESN的預(yù)測精度出發(fā),提出使用自適應(yīng)回溯搜索算法(Adaptive Backtracking Search Optimization Algorithm,ABSA)對ESN的輸出連接權(quán)值矩陣進行優(yōu)化.

1 相關(guān)知識

1.1 回聲狀態(tài)網(wǎng)絡(luò)

回聲狀態(tài)網(wǎng)絡(luò)因為其相對簡單的網(wǎng)絡(luò)結(jié)構(gòu)、訓(xùn)練算法和性能而廣受關(guān)注.ESN是儲備池計算方法之一,采用“儲備池”作為信息處理媒介,儲備池將網(wǎng)絡(luò)的輸入信號映射到高維的復(fù)雜動態(tài)狀態(tài)空間.儲備池的神經(jīng)元之間的連接在網(wǎng)絡(luò)初始化階段隨機生成并在整個訓(xùn)練過程中保持不變[12].正是由于儲備池計算特征,ESN相對于傳統(tǒng)的RNN具有明顯的優(yōu)勢.標準結(jié)構(gòu)的ESN如圖1所示,可以分為3個組成部分:一個輸入層(K個神經(jīng)元),一個儲備池(N個神經(jīng)元)和一個輸出 層(L個神經(jīng)元).

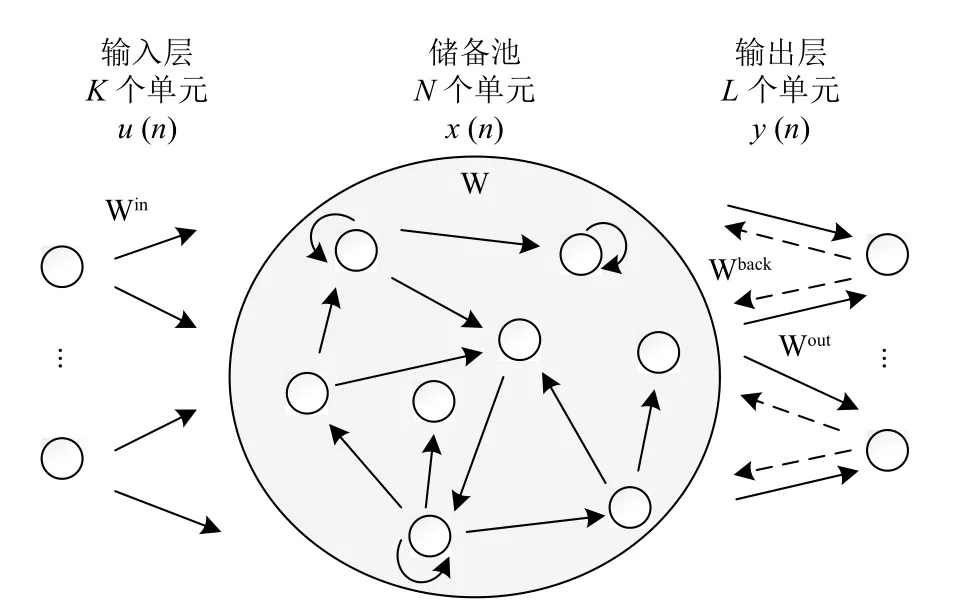
圖1 回聲狀態(tài)網(wǎng)絡(luò)的標準結(jié)構(gòu)

ESN在時刻n的輸入,儲備池神經(jīng)元的狀態(tài)和輸出層神經(jīng)元輸出分別表示如下:

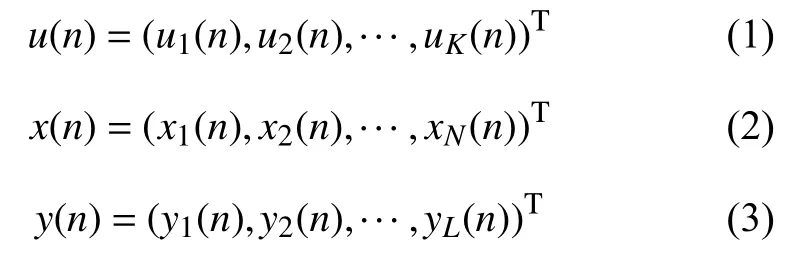
如圖1所示,在標準結(jié)構(gòu)的ESN中,當(dāng)輸入信號u(n+1)輸 入到網(wǎng)絡(luò)時,儲備池內(nèi)部神經(jīng)元在時刻n+1的狀態(tài)和網(wǎng)絡(luò)的輸出分別按照方程(4)和(5)進行更新:

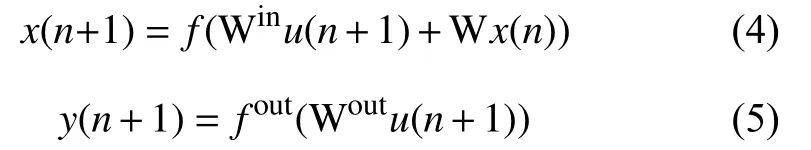
其中,Win(Win∈RN×K)、W (W∈RN×N)和Wout(Wout∈RL×N)分別代表網(wǎng)絡(luò)的輸入層到儲備池、儲備池內(nèi)部神經(jīng)元和儲備池到輸出層之間的連接權(quán)值矩陣.f=[f1,f2,···,fN]表示儲備池中神經(jīng)元的輸出函數(shù).一般來說,fi(i=1,2,···,N)采用“S-型”函數(shù),比如雙曲正切函數(shù) tanh .fout=[f1out,f2out,···,fLout]表示網(wǎng)絡(luò)輸出層神經(jīng)元的輸出函數(shù).通常情況下,fiout(i=1,2,···,L)會取恒等函數(shù).

1.2 回溯搜索算法及其改進

回溯搜索算法(Backtracking Search optimization Algorithm,BSA)是由Civicioglu在2013年提出的一種屬于進化算法范疇的新智能算法[13].BSA自從被提出就吸引了眾多學(xué)者進行研究并應(yīng)用到不同的領(lǐng)域,比如數(shù)值優(yōu)化[13,14]、自動發(fā)電控制[15]和功率流[16]等.標準的BSA主要包括5個基本算子:初始化(Initialization)、選擇I (Selection-I)、變異(Mutation)、交叉(Crossover)和選擇II (Selection-II),其算法流程如圖2所示.

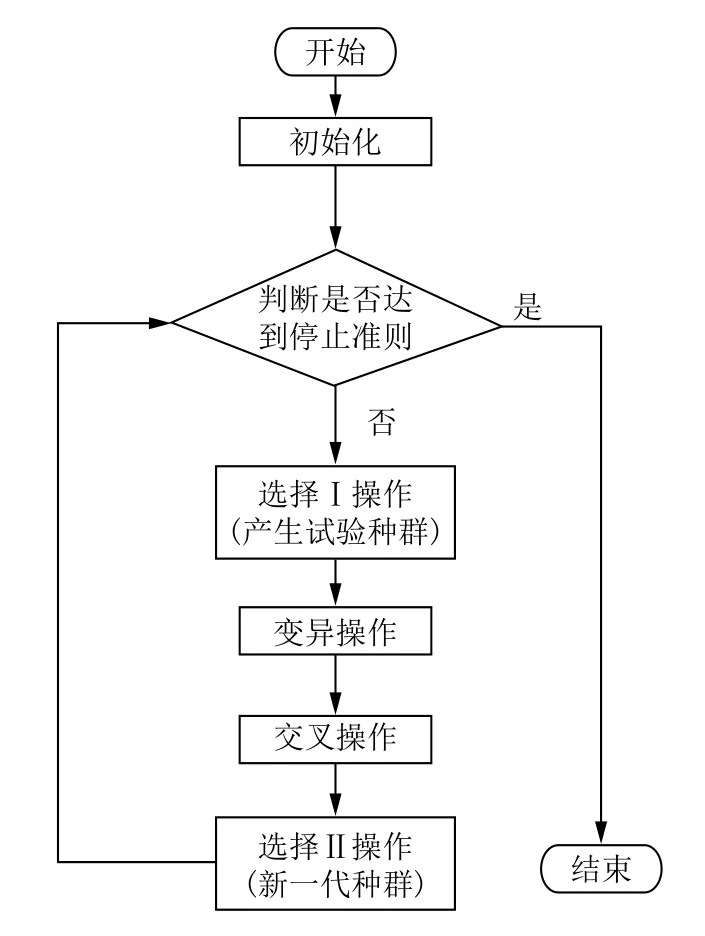
圖2 標準BSA算法流程

在標準BSA中,變異因子F在初始化過程中隨機給定并在整個過程中保持不變,這種策略不能平衡BSA算法的搜索能力和收斂性之間的關(guān)系.如果變異因子F取值大,BSA的全局搜索能力會很強而獲得的全局最優(yōu)解可能展現(xiàn)出低精度.如果變異因子F取值小,BSA在迭代過程中會加速收斂而其全局搜索能力會減弱.可以說,變異因子F是平衡BSA的全局搜索能力和收斂性的關(guān)鍵參數(shù).為了充分考慮變異因子F對BSA性能的影響,本文提出自適應(yīng)回溯搜索算法(ABSA).ABSA使用自適應(yīng)變異因子策略去替換標準的隨機給定策略,其策略方程表達如式(6)所示:

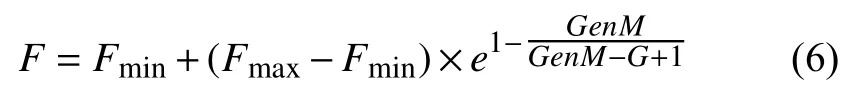
其中,Fmax和Fmin分別代表變異因子F的最大值和最小值.GenM是BSA的最大迭代次數(shù),G是當(dāng)前迭代次數(shù).e是自然常數(shù).從式(6)可以得出:變異因子 的取值是隨算法迭代過程的進行而不斷改變的.在開始迭代階段,F取值較大用于擴大搜索范圍,保證搜索時種群的多樣性;在隨后的迭代過程中,變異因子F取值逐漸變小,種群的搜索范圍將縮小且種群中已經(jīng)獲得的優(yōu)秀個體將會以較大概率被保留.

2 預(yù)測模型

2.1 模型介紹

為了驗證本文擬采用的自適應(yīng)回溯搜索算法優(yōu)化回聲狀態(tài)網(wǎng)絡(luò)(ABSA_ESN)的性能,將設(shè)計其他的四種預(yù)測模型用于與ABSA_ESN進行比較.具體而言,本文將設(shè)計以下5種預(yù)測模型:

(1)ESN.標準的ESN模型.

(2)GA_ESN.使用遺傳算法(Genetic Algorithm,GA)優(yōu)化ESN輸出連接權(quán)值矩陣.

(3)DE_ESN.使用差分進化算法(Differential Evolution,DE)優(yōu)化ESN輸出連接權(quán)值矩陣.

(4)BSA_ESN.使用標準回溯搜索算法(BSA)優(yōu)化ESN輸出連接權(quán)值矩陣.

(5)ABSA_ESN.使用自適應(yīng)回溯搜索算法(ABSA)優(yōu)化ESN輸出連接權(quán)值矩陣.

以上5種預(yù)測模型中,GA_ESN、DE_ESN、BSA_ESN和ABSA_ESN是四個優(yōu)化的ESN模型.其中,GA、DE、BSA和ABSA都屬于進化算法(Evolutionary Algorithm,EA)的范疇.

2.2 ESN的優(yōu)化流程

利用ABSA (GA,DE或者BSA)優(yōu)化ENS的輸出連接權(quán)值矩陣Wout的流程圖如圖3所示.

ESN的Wout優(yōu)化流程分為以下幾個步驟:

Step 1.設(shè)置ESN參數(shù)并收集網(wǎng)絡(luò)輸入產(chǎn)生的狀態(tài)矩陣.

Step 2.設(shè)置ABSA (GA,DE或BSA)的參數(shù)并生成初始化種群.設(shè)置ABSA的初始迭代代數(shù)G=0.

Step 3.判斷ABSA (GA,DE或BSA)的迭代是否達到最大迭代次數(shù).如果當(dāng)前迭代次數(shù)G等于最大迭代次數(shù)GenM,則ABSA (GA,DE或BSA)的迭代過程結(jié)束,獲得最優(yōu)種群和最優(yōu)個體;否則,流程繼續(xù)執(zhí)行.

Step 4.依次執(zhí)行ABSA (GA,DE或BSA)的選擇I (或沒有)、自適應(yīng)變異(或變異)、交叉和選擇II (或選擇)等幾個操作,獲得當(dāng)前迭代過程G的新種群.

Step 5.計算新種群中每個個體的適應(yīng)值,按照貪婪選擇原則更新當(dāng)前迭代過程的種群.比較當(dāng)前迭代過程獲得的最優(yōu)個體與當(dāng)前獲得的全局最優(yōu)個體的適應(yīng)值,適應(yīng)值較小的將作為新的全局最優(yōu)適應(yīng)值且相應(yīng)的個體更新為全局最優(yōu)個體.

Step 6.更新G=G+1.返回Step 3.

Step 7.將進化算法獲得的最優(yōu)個體設(shè)置為ESN的最優(yōu)輸出連接權(quán)值矩陣Wout,ESN網(wǎng)絡(luò)訓(xùn)練完成.

Step 8.將測試集中樣本按順序輸入到訓(xùn)練好的E SN中,進行預(yù)測.

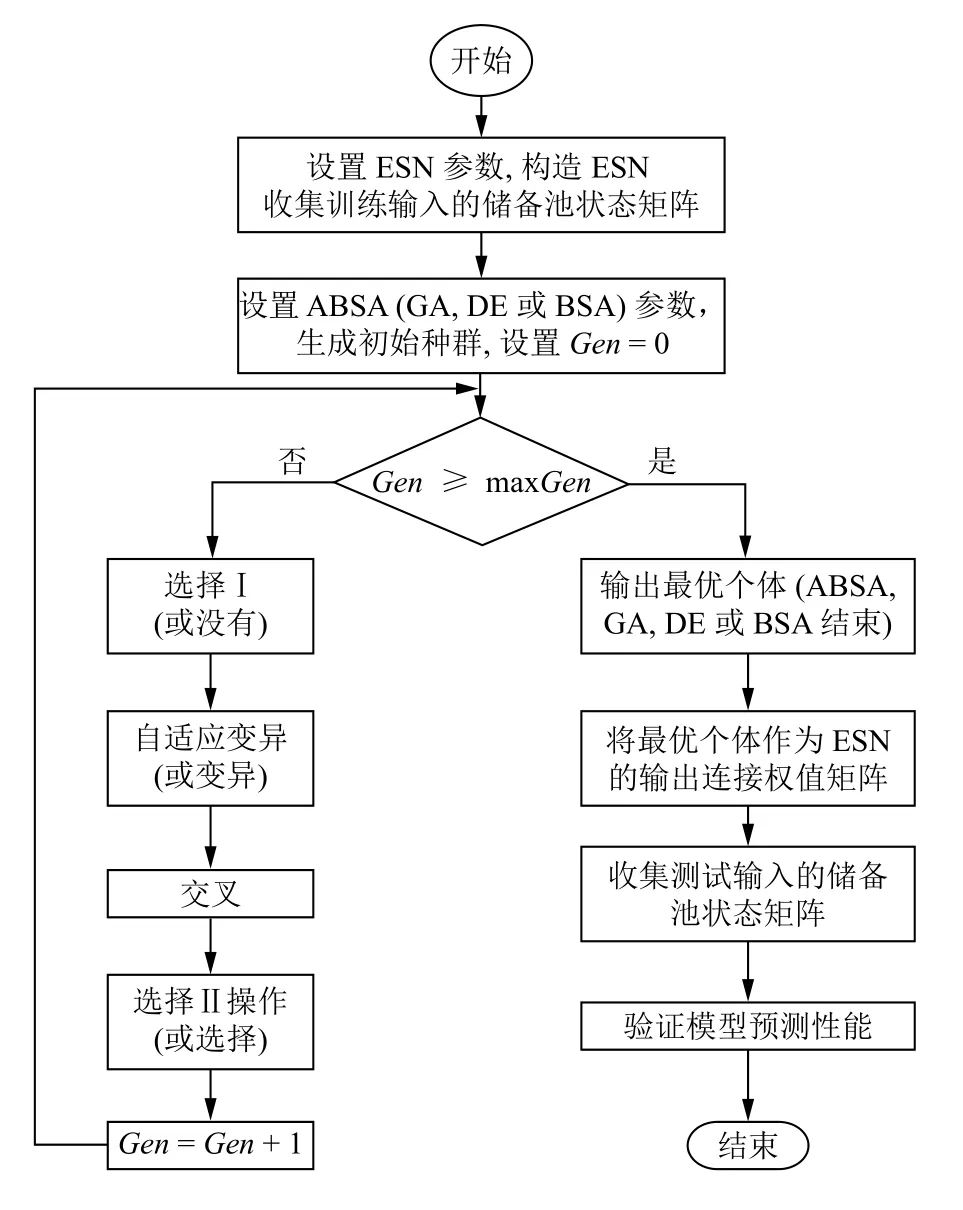
圖3 利用ABSA (GA,DE或BSA)優(yōu)化ESN的Wout的流程圖

2.3 模型合理性分析及模型比較

本文所采用的5種模型的建模方法在上述2.1和2.2小節(jié)已經(jīng)介紹.本小節(jié)將對5種模型進行比較并討論選擇它們的合理性.

(1)ESN是最先進的時間序列預(yù)測模型之一.ESN因為其網(wǎng)絡(luò)結(jié)構(gòu)簡單、訓(xùn)練效率高且耦合“時間參數(shù)”,因而能夠有效地應(yīng)用于時間序列預(yù)測問題研究.然而,標準的ESN計算地輸出連接權(quán)值矩陣容易致使網(wǎng)絡(luò)陷入過擬合狀態(tài),影響ESN性能的發(fā)揮.

(2)GA_ESN,DE_ESN和BSA_ESN是優(yōu)化的ESN預(yù)測模型.GA、DE和BSA 3種智能算法的算法流程、算子和參數(shù)個數(shù)不盡相同.使用3種智能算法對ESN進行優(yōu)化的目的是克服標準ESN容易陷入網(wǎng)絡(luò)過擬合狀態(tài)的缺陷,增加優(yōu)化方法的多樣性.相對于GA和DE,BSA在全局尋優(yōu)時只有一個參數(shù)需要設(shè)定,在很大程度上能夠簡化算法參數(shù)設(shè)置過程,進而節(jié)約計算成本.

(3)ABSA_ESN是采用改進BSA優(yōu)化的ESN預(yù)測模型.標準BSA的參數(shù)變異因子在算法初始化過程中隨機給定并在整個過程中保持不變,這種策略難以平衡BSA算法的搜索能力和收斂速率.ABSA是采用自適應(yīng)變異因子策略改進的BSA,其能夠有效地克服上述缺陷.具體而言,ABSA在迭代初期變異因子取值較大,能夠擴大搜索范圍從而保證種群的多樣性.此時,ABSA的收斂速度較慢且收斂精度較低.隨著迭代過程的進行,變異因子的取值將逐漸變小,種群的搜索范圍將圍繞已經(jīng)獲得的優(yōu)秀個體展開以保證優(yōu)秀個體將會以較大概率被保留.此時,ABSA的收斂速度和收斂精度逐步加快和提高.總體而言,ABSA_ESN在算法的參數(shù)設(shè)置、收斂速度和收斂精度上較GA_ESN,DE_ESN和BSA_ESN等均有優(yōu)勢.

3 數(shù)值實驗和結(jié)果分析

3.1 實驗設(shè)置

為了驗證本文所提出的ABSA_ESN和其他四個用于對比的模型預(yù)測性能,兩個混沌時間序列將被采用作為實驗數(shù)據(jù)集.完成所有實驗的個人電腦配置如下:操作系統(tǒng)是64位Windows 10專業(yè)版、處理器是Intel(R)Core(TM)i7-7700 CPU @3.6 GHz和內(nèi)存為16 GB.運行實驗的軟件環(huán)境是Python 3.6和Matlab 2016b.

3.2 數(shù)據(jù)集及性能評估標準

本文將采用兩個混沌時間序列數(shù)據(jù)集用于驗證所提出的五種預(yù)測模型的性能.第一個混沌時間序列是非線性自回歸滑動模型(Nonlinear Autoregressive Moving Average,NARMA),這是一種有輸入的非線性自回歸移動平均數(shù)數(shù)列,該模型已經(jīng)成功應(yīng)用于非線性系統(tǒng)[17].第二個混沌時間序列是Mackey-Glass時間序列[18].以上兩個時間序列模型經(jīng)常被使用作為測試時間序列預(yù)測算法的性能.

3.2.1 NARMA模型

NARMA模型方程式表示如下:

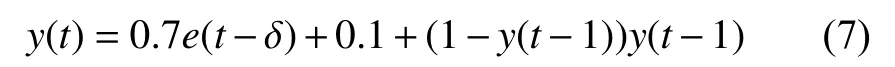
其中,e(t)為獨立分布在( 0,1)之 間的時刻t的模型輸入,y(t)是時刻t的模型輸出,δ 為時滯參數(shù).通常取δ =3.

在本實驗中,我們設(shè)定NARMA模型的樣本大小為1000.訓(xùn)練集、驗證集和測試集樣本的產(chǎn)生過程如下:首先,隨機產(chǎn)生1000個取值范圍在( 0,1)的樣本作為系統(tǒng)輸入e(t).根據(jù)式(7)計算出NARMA方程式相應(yīng)的期望輸出y(t).第二,分別取系統(tǒng)輸入樣本和期望輸出樣本的前80%(樣本編號1–800)樣本作為訓(xùn)練集樣本.第三,緊接著選取10%(樣本編號801–900)樣本作為確定回聲狀態(tài)網(wǎng)絡(luò)模型結(jié)構(gòu)的驗證樣本.最后,選取剩余10%(樣本編號901–1000)樣本作為預(yù)測集樣本.本文設(shè)計驗證集的主要目的是為了在訓(xùn)練階段選擇合適的ESN模型結(jié)構(gòu).含有1000個樣本的系統(tǒng)輸入如圖4及其對應(yīng)的系統(tǒng)輸出如圖5所示.

圖4 NARMA模型輸入序列

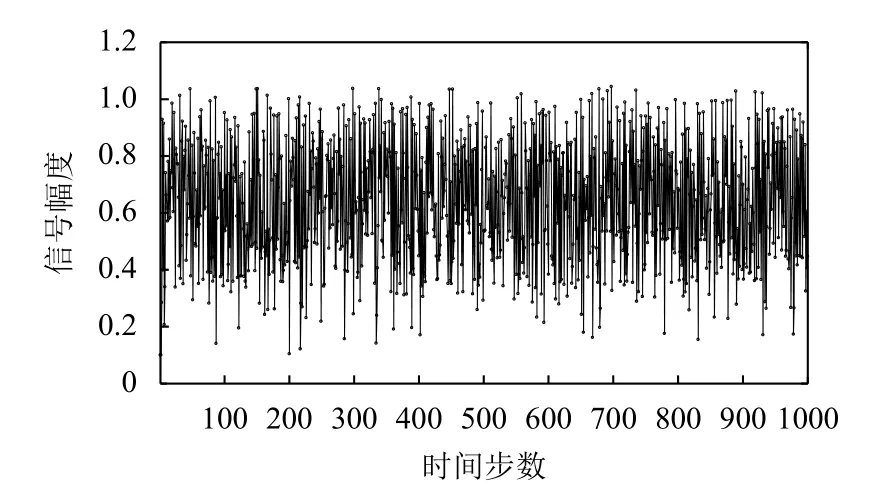
圖5 NARMA模型輸出序列

3.2.2 Mackey-Glass混沌系統(tǒng)

Mackey-Glass時間序列是從時延差分系統(tǒng)導(dǎo)出,其方程如式(8)所示:

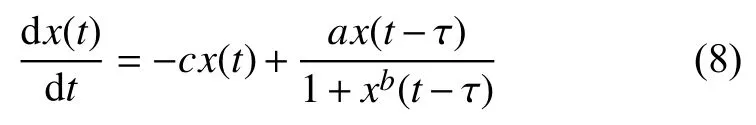
其中,x(t)是時間序列在時刻t時的取值.a、b和c為參數(shù),通常取a=0.2、b=10 和c=0.1.Farmer對Mackey-Glass方程的行為特性做過深入研究,研究結(jié)果表明當(dāng)時滯參數(shù) τ>16.8 時 該方程呈現(xiàn)混沌性,并且τ 值越大,混沌程度越高[19].本文依照一般情況設(shè)置時滯參數(shù)取值為τ =17.

在本實驗中,我們設(shè)定Mackey-Glass時間序列樣本大小為1000.訓(xùn)練集、驗證集和測試集樣本的劃分同NARMA模型一樣,即編號1–800的樣本作為訓(xùn)練集,編號801–900的樣本作為驗證集和編號901–1000的樣本作為測試集.使用二階Runge-Kutta方法以步長為0.1構(gòu)造的樣本長度為1000的時間序列如圖6所示.

圖6 Mackey-Glass時間序列

3.2.3 性能評估標準

用于測量時間序列預(yù)測模型性能的指標多種多樣,本文將采用均方根誤差(Root Mean Square Error,RMSE)作為評估預(yù)測精度指標,其定義如式(9)所示:

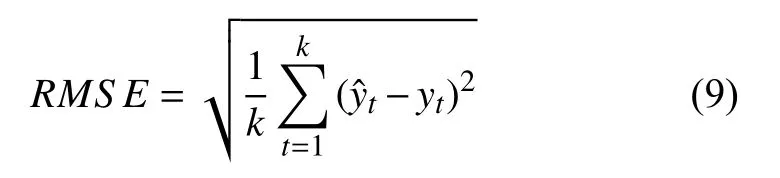
3.3 參數(shù)設(shè)置與分析

3.3.1 參數(shù)設(shè)置

本文所提出的預(yù)測模型的性能受ESN結(jié)構(gòu)選擇和相應(yīng)參數(shù)設(shè)置的影響.結(jié)合本文所使用的兩個時間序列數(shù)據(jù)集的特點,擬采用ESN的結(jié)構(gòu)參數(shù)如下:(1)輸入層單元的數(shù)目為2(在每個時刻t,ESN有一個常數(shù)輸入0.1);(2)儲備池的大小從集合{ 20,30,50}中選擇;(3)輸出層單元數(shù)目為1.ESN的其它的參數(shù),比如儲備池內(nèi)部連接權(quán)值矩陣譜半徑SR和儲備池稀疏性SP根據(jù)已有文獻的推薦進行設(shè)置,即SR=0.8 和SP=5%[12].輸入單元尺度IC及位移尺度IS分別設(shè)置為IC=0.3和IS=?0.2.

關(guān)于BSA和ABSA的參數(shù)設(shè)置主要是基于一列實驗和已有參考文獻的推薦.BSA和ABSA的具體參數(shù)設(shè)置如下:(1)種群大小均設(shè)置為100;(2)最大迭代次數(shù)均設(shè)置為100;(3)交叉概率mixrate均設(shè)置為1.0[13];(4)BSA的變異因子F設(shè)置為F=3?randn(randn∈N(0,1),N(0,1)是標準正太分布)[13],而ABSA的最大和最小的變異因子分別設(shè)置為0.9和0.1.另外,GA和DE的參數(shù)分別設(shè)置如下:(1)種群大小設(shè)置為100;(2)最大迭代次數(shù)設(shè)置為100;(3)交叉概率為0.6;(4)變異概率為0.01.

3.3.2 自適應(yīng)變異因子F取值分析

ABSA的變異因子F取值如圖7所示.從圖中可以看出,在算法迭代初期變異因子F取值較大(第一個迭代階段,F取值為最大設(shè)定值0.9).此時,ABSA的種群中的個體以較大概率進行變異,ABSA主要是在種群個體空間中進行全局尋優(yōu),形成的新種群個體隨機分布在個體空間之中且個體之間的關(guān)聯(lián)性較小.可以說,ABSA在迭代初期的全局尋優(yōu)能力非常強而局部尋優(yōu)能力非常弱,種群個體的相似性很小.隨著迭代過程的更迭,變異因子F取值逐步減小,ABSA種群中的優(yōu)秀個體逐漸沉淀并且這些優(yōu)秀個體以逐漸減小的概率進行變異.此時,ABSA逐漸由全局尋優(yōu)轉(zhuǎn)變?yōu)榫植繉?yōu).新種群的形成主要是圍繞已經(jīng)獲得的優(yōu)秀個體進行局部尋優(yōu).即隨著迭代的進行,ABSA的局部尋優(yōu)能力逐漸加強而全局尋優(yōu)能力逐漸減弱,種群個體的相似性逐漸加強.直到迭代進行到后期(圖7中的迭代次數(shù)達到90次左右),變異因子F取值趨于穩(wěn)定(最小設(shè)定值0.1),ABSA已經(jīng)由全局尋優(yōu)過渡到局部尋優(yōu).此時,ABSA全局尋優(yōu)能力非常弱而局部尋優(yōu)能力非常強.所以,ABSA的自適應(yīng)變異因子取值策略能夠平衡算法的全局尋優(yōu)能力和局部尋優(yōu)能力.

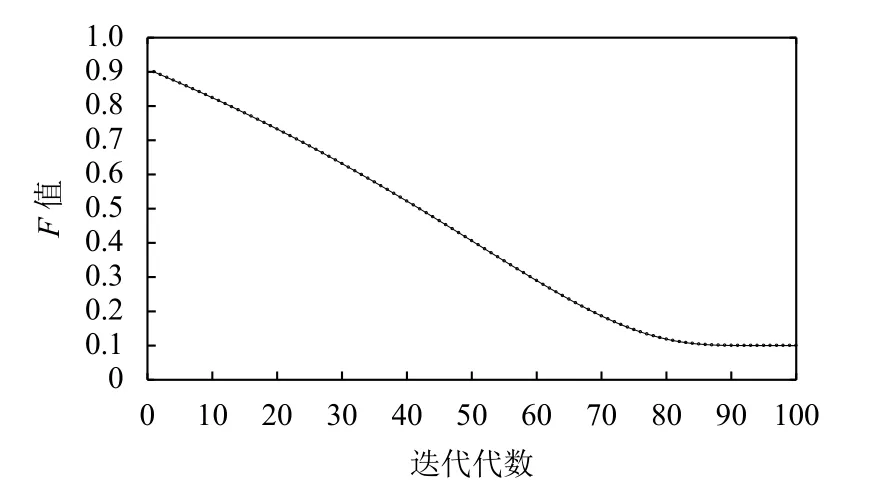
圖7 ABSA的變異因子F取值曲線

3.4 參數(shù)設(shè)置與分析

對于本文所使用的5個預(yù)測模型中的每個預(yù)測模型,在訓(xùn)練階段由于ESN儲備池大小不同而會設(shè)計3個候選模型結(jié)構(gòu),并且根據(jù)驗證集的結(jié)果選擇一個最優(yōu)模型結(jié)構(gòu)作為該預(yù)測模型的最優(yōu)結(jié)構(gòu).表1給出所有5種預(yù)測模型的最優(yōu)模型結(jié)構(gòu).5種預(yù)測模型在兩個時間序列數(shù)據(jù)集上的性能分別如圖8 (NARMA模型)和圖9 (Mackey-Glass混沌系統(tǒng))所示,其中“Actual”代表時間序列數(shù)據(jù)集的期望值.在以RMSE為誤差度量評價標準的前提下,5種預(yù)測模型在兩個時間序列數(shù)據(jù)集上的誤差如表2所示(最優(yōu)的預(yù)測結(jié)果用黑體特別標注).

表1 5種預(yù)測模型的最優(yōu)模型結(jié)構(gòu)

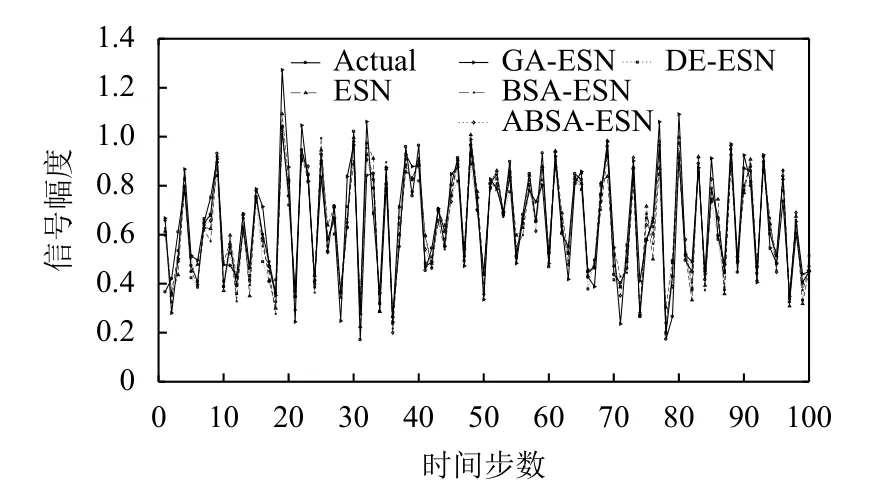
圖8 NARMA上5種模型的預(yù)測值和期望值

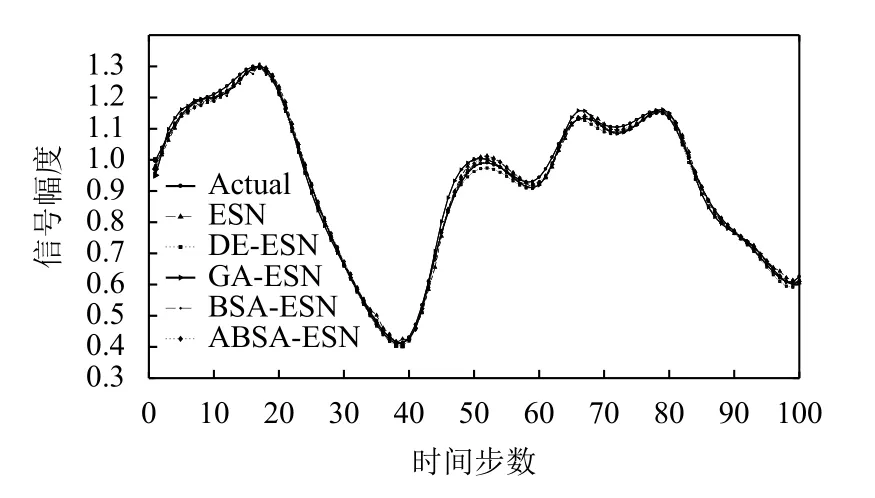
圖9 Mackey-Glass上5種模型的預(yù)測值和期望值

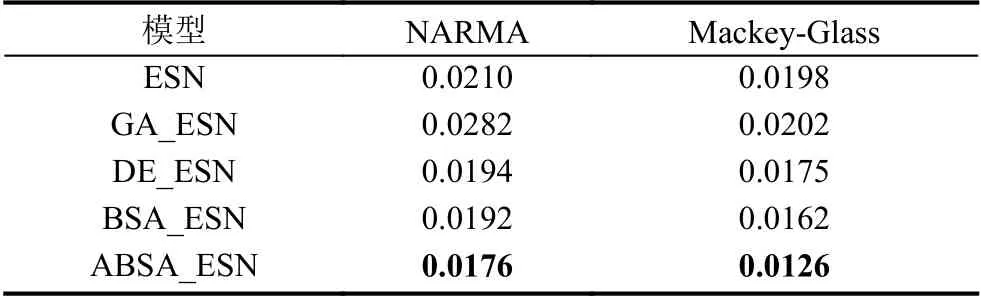
表2 5種預(yù)測模型的最優(yōu)結(jié)果(以RMSE為度量方式)

為了評估兩個相比較模型之間的性能差異,相對誤差將被采用作為度量方法.相對誤差是一種流行的用于比較兩個方法之間的性能的度量方法[20].對于兩種方法A(基本方法)和B(對比方法),其誤差分別記為δA和 δB,則相對誤差為相對誤差小于0,說明對比方法B比基本方法A性能更優(yōu).另外,相對誤差的平均指兩種比較方法在兩個或兩個以上數(shù)據(jù)集上的相對誤差的平均值.相對誤差的均值小于0說明對比方法B相對于基本方法A在所有數(shù)據(jù)集上預(yù)測性能有改進.

3.4.1 優(yōu)化的ESN與標準的ESN

在本文中,為了驗證所提出的使用進化算法優(yōu)化的ESN (GA_ESN、DE_ESN、BSA_ESN和ABSA_ESN)與標準的ESN之間的預(yù)測性能差異,將使用標準的ESN作為基本方法,使用GA_ESN、DE_ESN、BSA_ESN和ABSA_ESN作為對比方法進行預(yù)測性能比較.表3給出了兩兩比較模型之間的相對誤差.

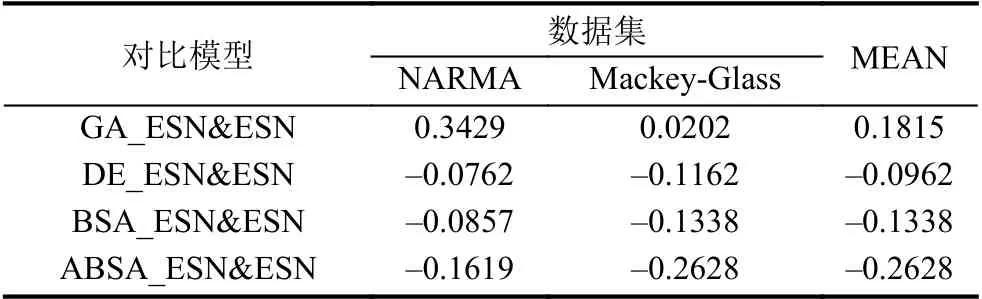
表3 兩種比較模型之間相對誤差(以ESN為基本方法)

從表3可以得出:標準的ESN預(yù)測模型無論是在單個數(shù)據(jù)集還是在兩個數(shù)據(jù)集作為整體的性能評估中,其性能都只比GA_ESN優(yōu)越而比DE_ESN、BSA_ESN和ABSA_ESN等預(yù)測模型差.具體而言,GA_ESN相對于ESN的性能單獨在NARMA和Mackey-Glass上分別下降34.29%和2.02%,在兩個數(shù)據(jù)集的整體性能上平均下降18.15%(如表3最后一列“MEAN”所示).而DE_ESN、BSA_ESN和ABSA_ESN相對于ESN單獨在兩個數(shù)據(jù)集上的性能分別提升7.62%/11.62%、8.57%/18.18%和16.19%/36.36%,在兩個數(shù)據(jù)集的整體性能上平均提升9.62%,13.38%和26.28%(如表3最后一列“MEAN”所示).總體來說,使用進化算法對ESN的輸出連接權(quán)值矩陣Wout進行優(yōu)化能夠提升ESN的預(yù)測性能.

3.4.2 ABSA_ESN與其他4種模型

由3.4.1小節(jié)可知,使用進化算法對ESN的輸出連接權(quán)值矩陣Wout進行優(yōu)化相對于標準的ESN具有一定的性能優(yōu)勢.本節(jié)將具體討論本文所提出的ABSAESN相對于標準的ESN和其他3種優(yōu)化的ESN的優(yōu)勢體現(xiàn).具體而言,將ABSA-ESN作為對比方法,而ESN、GA-ESN、DE-ESN和BSA-ESN等分別作為基本方法,然后比較它們兩兩之間的模型性能.表4列出了兩兩相比較模型之間的相對誤差.

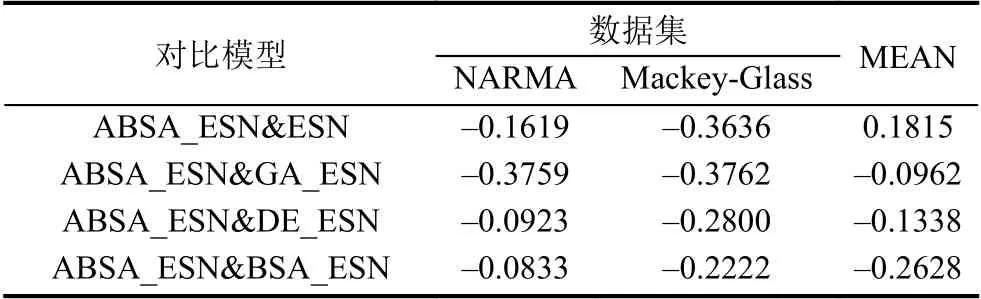
表4 兩種比較模型之間相對誤差(以ABSA_ESN為對比方法)

從表4可以得出:ABSA_ESN預(yù)測模型比所提出的其他4種預(yù)測模型ESN、GA_ESN、DE_ESN和BSA_ESN的預(yù)測精度大幅提升,具體體現(xiàn)在以下兩個方面:

(1)當(dāng)單獨關(guān)注NARMA或者Mackey-Glass數(shù)據(jù)集時,ABSA_ESN能夠比ESN、GA_ESN、DE_ESN和BSA_ESN等模型在兩個數(shù)據(jù)集上都能獲得更好的預(yù)測結(jié)果,主要表現(xiàn)在ABSA_ESN在兩個數(shù)據(jù)集上的預(yù)測精度提升比例分別為16.19%/36.36%、37.59%/37.62%、9.23%/28%和8.33%/22.22%.

(2)當(dāng)關(guān)注所有5種預(yù)測模型在兩個數(shù)據(jù)集上的總體性能時,ABSA_ESN模型比其他4個模型在預(yù)測精度上也有大幅提升.ABSA_ESN模型相對于ESN、GA_ESN、DE_ESN和BSA_ESN等模型的平均相對誤差提升比例分別為26.28%、37.61%、18.64%和15.28%.這個信息如表4中最后一列“MEAN”所示.

由此可見,本文提出的使用自適應(yīng)回溯搜索算法優(yōu)化的回聲狀態(tài)網(wǎng)絡(luò)模型(ABSA_ESN)能夠比未優(yōu)化的回聲狀態(tài)網(wǎng)絡(luò)模型(ESN)和采用其他進化算法優(yōu)化的回聲狀態(tài)網(wǎng)絡(luò)模型(GA_ESN、DE_ESN和BSA_ESN)在兩個混沌時間序列數(shù)據(jù)集上獲得更好的預(yù)測精度.

4 結(jié)束語

本文提出使用自適應(yīng)回溯搜索算法優(yōu)化回聲狀態(tài)網(wǎng)絡(luò)的時間序列預(yù)測模型(ABSA_ESN),以解決標準回聲狀態(tài)網(wǎng)絡(luò)中使用的線性方法求解輸出連接權(quán)值矩陣容易陷入過擬合的問題,從而提升回聲狀態(tài)網(wǎng)絡(luò)的預(yù)測性能.為了驗證本文所提出ABSA_ESN在時間序列預(yù)測問題上的可行性和有效性,本文還設(shè)計了4種預(yù)測模型用于比較,它們分別是標準的回聲狀態(tài)網(wǎng)絡(luò)(ESN)、遺傳算法的優(yōu)化回聲狀態(tài)網(wǎng)絡(luò)(GA_ESN)、差分進化算法優(yōu)化的回聲狀態(tài)網(wǎng)絡(luò)(DE_ESN)和標準回溯搜索算法優(yōu)化的回聲狀態(tài)網(wǎng)絡(luò)(BSA_ESN).通過對實驗結(jié)果進行分析可以得出如下結(jié)論:(1)使用進化算法優(yōu)化的ESN (GA_ESN、DE_ESN、BSA_ESN和ABSA_ESN)相對于標準的ESN在預(yù)測性能上具有一定的優(yōu)勢;(2)ABSA_ESN相對于4種對比模型能夠獲得更好的預(yù)測精度.值得注意的是本文使用的是基本結(jié)構(gòu)的回聲狀態(tài)網(wǎng)絡(luò),其自身性能可能會受到一定的限制.在未來,可以研究使用其他更加有效的進化算法優(yōu)化具有復(fù)雜結(jié)構(gòu)的回聲狀態(tài)網(wǎng)絡(luò)的輸出連接權(quán)值矩陣,進一步提升回聲狀態(tài)網(wǎng)絡(luò)的性能.