一種八推進器水下機器人動力學分析

李卓禹，張志強，周宏偉

（1.海軍研究院，北京 100161；2.復雜艦船系統仿真重點實驗室，北京 100161；3.海軍工程大學，湖北 武漢 430033）

0 引言

目前，各國對水下機器人的航行研究越來越重視[1-2]。水下機器人可以在軍用和民用的多個領域發揮重要作用，水下機器人的發展和優化涉及多方面技術[3]，其中水下機器人的空間運動動力學數學模型是進行水下機器人總體性能、彈道、控制和導航系統研究、設計與仿真的基本前提和重要依據。

水下機器人的運動已由早期單純的平動逐步強化為有多個自由度的空間運動[4]，其中的典型樣式是裝有8個推進器（4個垂直電機、4個水平電機四角對峙布置）的水下機器人。該型機器人能夠進行3個維度上的平移運動以及繞三軸的轉動，具備6個自由度運動能力；同時，8個推進器在四角對稱布置，該型水下機器人的靈活性及穩定性都得到了較好保證，是應用范圍很廣泛的機器人類型。本文以該型機器人為研究對象，對其進行動力學分析，分析方法及結果對其它類型水下機器人有較好的借鑒意義。

1 水下機器人坐標系建立與轉換

論文研究對象為某型質量m=20 kg，并具有8個推進器的水下機器人，如圖1所示。4個垂直布置的螺旋槳成正方形分布，4個水平布置的螺旋槳成45°角對峙分布。在俯視圖中可以看出水下機器人中間有一凹槽，凹槽是半徑R=0.25 m的圓柱，其主要參數見表1。

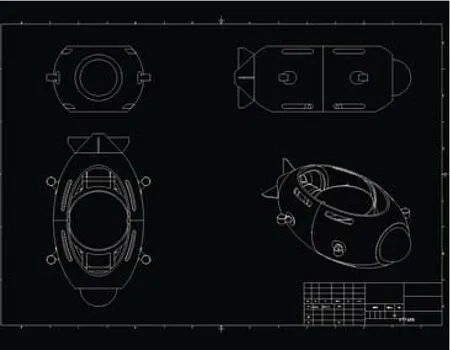
圖1 水下機器人三視圖及立體圖Fig.1 Three views and stereogram of underwater robot

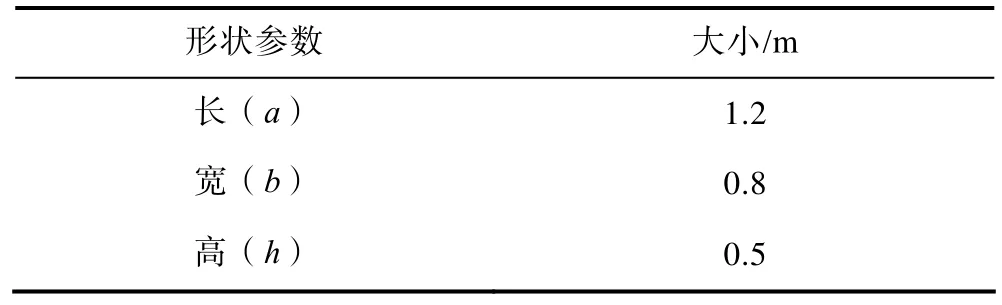
表1 水下機器人形狀參數Table 1 Shape parameters of underwater robot

1.1 坐標系建立與參數描述

水下機器人空間運動的坐標系一般采用慣性坐標系和隨動坐標系兩種坐標系 。通過慣性坐標系描述水下機器人的運動軌跡及姿態，通過隨動坐標系描述水下機器人的水動力特性。

慣性坐標系：一般采用地面坐標系O-xyz，與地球表面固連，原點O為水下機器人出發點；Ox軸處于通過O點的地平面內，指向任意方向（本文取水下機器人的初始航向）；Oz軸在通過Ox軸的鉛錘面內與Ox軸垂直，向下為正；Oy軸按右手定則確定。

隨動坐標系：一般采用體坐標系A-x1y1z1，原點A與水下機器人重心重合；Ax1軸與水下機器人縱軸重合，指向前部為正；Az1軸在水下機器人的縱向對稱面內，垂直于Ax1軸，指向下方為正；Ay1軸按右手定則確定。

在慣性坐標系中水下機器人的位置可以表示為P=x,y,z］T∈R3；水下機器人的姿態可以表示為 Θ =［φ,θ,ω］T∈S3；在體坐標系中速度描述為V=［u,v,w］T∈R3，角速度表示為ωb=［p,q,r］T∈R3；水下機器人所受力與所受力矩在水下機器人體坐標系中分別描述為F=［X,Y,Z］T∈R3與M=［K,M,N］T∈R3。

1.2 慣性坐標系與隨動坐標系的轉換

水下機器人的航行軌跡需要在慣性坐標系中進行計算。同時，由于水下機器人的運動參數都是在隨動坐標系，不能直接運用牛頓第二定律建立運動方程，所以需要將水下機器人的運動參數轉換到慣性坐標系中，建立水下機器人的運動學方程[6]。這涉及慣性坐標系O-xyz與隨動坐標系A-x1y1z1的轉換。

為方便研究，可假設兩坐標系的原點O與A重合，水下機器人在坐標系O-xyz的空間位置坐標為P（x,y,z），在坐標系A-x1y1z1的空間位置坐標為P1(x1,y1,z1)。同時Ox與Ax1的夾角為φ，Oy軸與Ay1軸的夾角為θ，Oz軸與Az1軸的夾角為ψ，則兩坐標系之間的轉換矩陣為

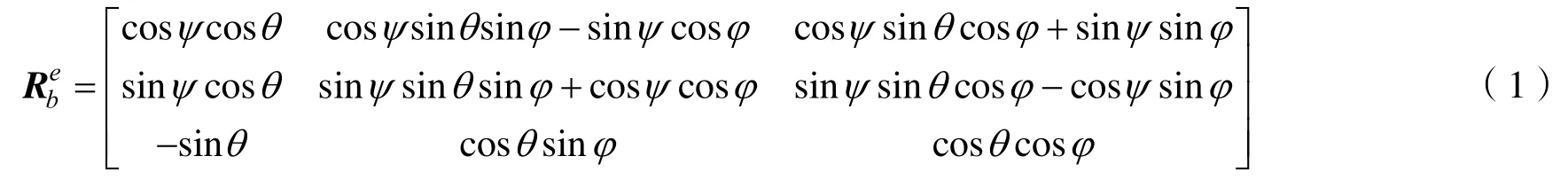
由于2個直角坐標系全部為正交系，故轉換矩

當歐拉角很小時，運用極限定理忽略二階小量將轉換矩陣簡化為

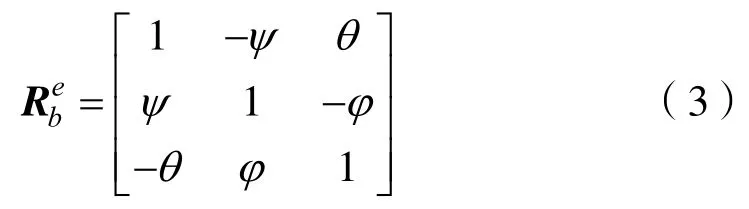
則有

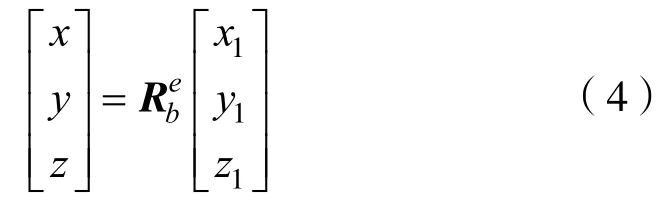
由兩坐標系的轉換關系，得歐拉角與隨動坐標系的角速度的轉換矩陣為

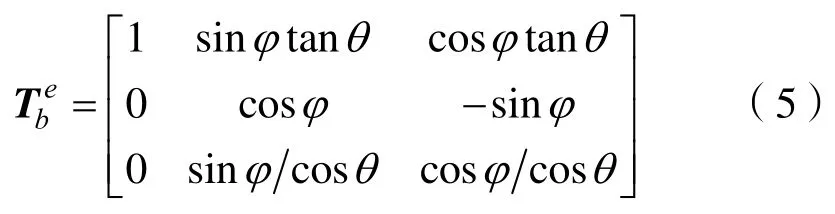
當歐拉角很小時，運用極限定理忽略二階小量將轉換矩陣簡化為

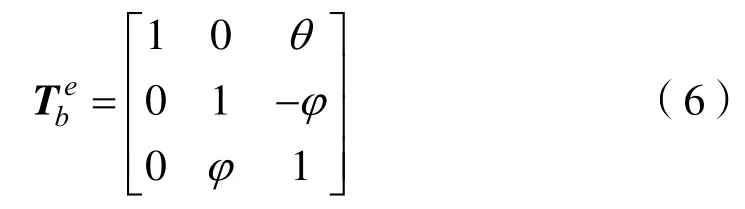
從上述式子看出θ≠±9 0o，且。

2 水下機器人動力學方程

推導水下機器人的動力學方程之前，首先提出下列假設：1）水下機器人為絕對剛體；2）將地面坐標系視為慣性坐標系；3）水下機器人完全浸沒在流體介質中，并完全處于全粘濕狀態；4）假設水下機器人的8個推進器所產生的推力大小一樣，控制信號大小一樣，且推進器正反轉所產生的推力大小一樣；5）假設水下機器人在水中不受其他外力處于懸停狀態，即重力等于浮力。

將水下機器人視為絕對剛體，在推導水下機器人的動力學方程時，可以不考慮水下機器人質量內部的相互作用力，忽略其微小的變形；本文研究的基于多推進器的水下機器人速度低、航程短，故只考慮水下機器人所受到的流體作用力。綜上假設，水下機器人航行時所受到的力與力矩主要包括[7]：1）重力 G、所受浮力 B，以及2個力共同產生的靜力矩；2）螺旋槳所產生的推力T和力矩；3）水下機器人受到的流體作用力。

經過推導，可以得出靜力與靜力矩為

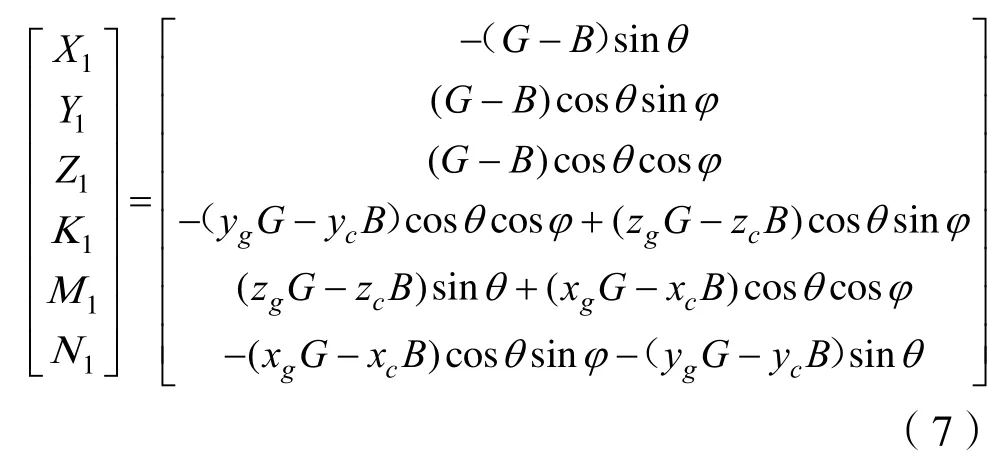
式中：(xg,yg, zg)為重心坐標；(xc, yc, zc)為浮心坐標；G為重力；B為浮力。假設重力G等于浮力B，又因隨動坐標系原點與水下機器人重心重合，故簡化得靜力與靜力矩得

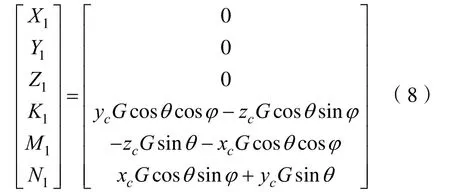
螺旋槳對水下機器人的推力及推力矩為[8]

式中：R1為4個垂直布置的螺旋槳中心距AZ1軸的距離；R2為4個水平布置的螺旋槳中心距AZ1軸的距離；KT為推力系數；ρ為水密度；n為螺旋槳轉速，r/min；D為螺旋槳直徑。水下機器人阻力為[9]

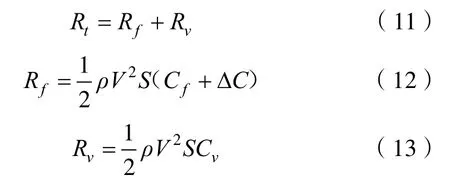
式中：Rf為摩擦阻力；Rv為形狀阻力；Cf為光滑表面的摩擦阻力系數；Cv為形狀阻力系數；CΔ為表面粗糙度的附加阻力系數；ρ為水的密度；V為水下機器人航行速度；S為浸濕的面積。

流體作用力產生的力矩大小為

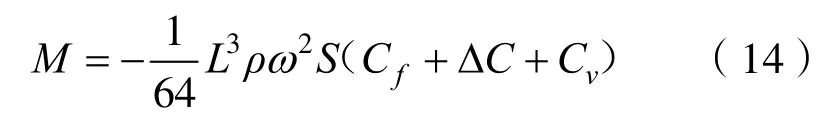
式中：L為特征長度；ρ為水的密度；ω為角速度；S為浸濕的面積；Cf為光滑表面的摩擦阻力系數；Cv為形狀阻力系數；CΔ為表面粗糙度的附加阻力系數。

由式（11）-（14）得水下機器人所受流體作用力與力矩為

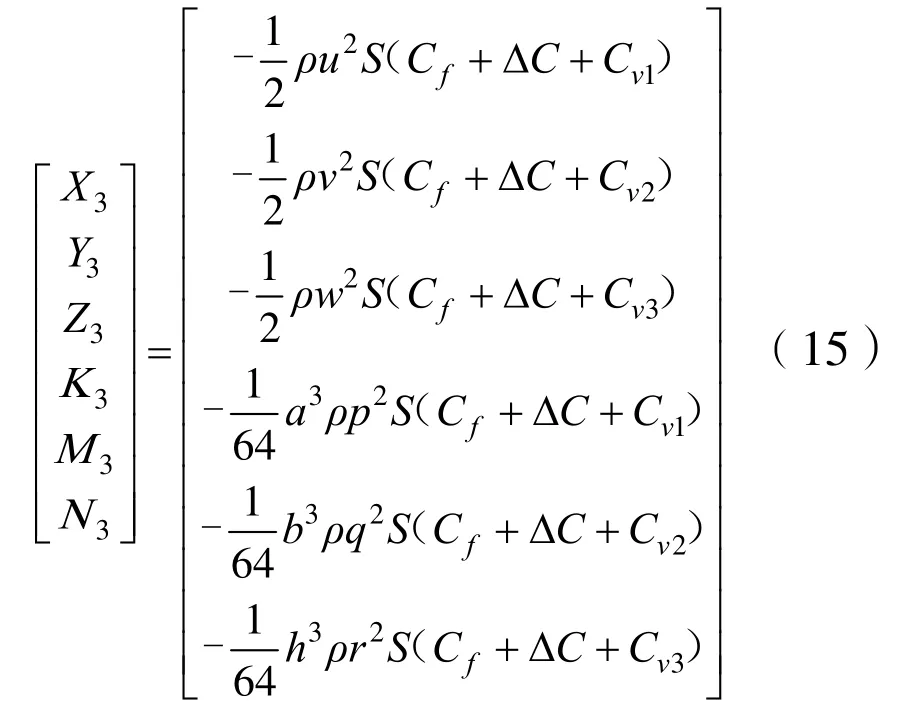
綜上所述，水下機器人所受到的力與力矩總和為

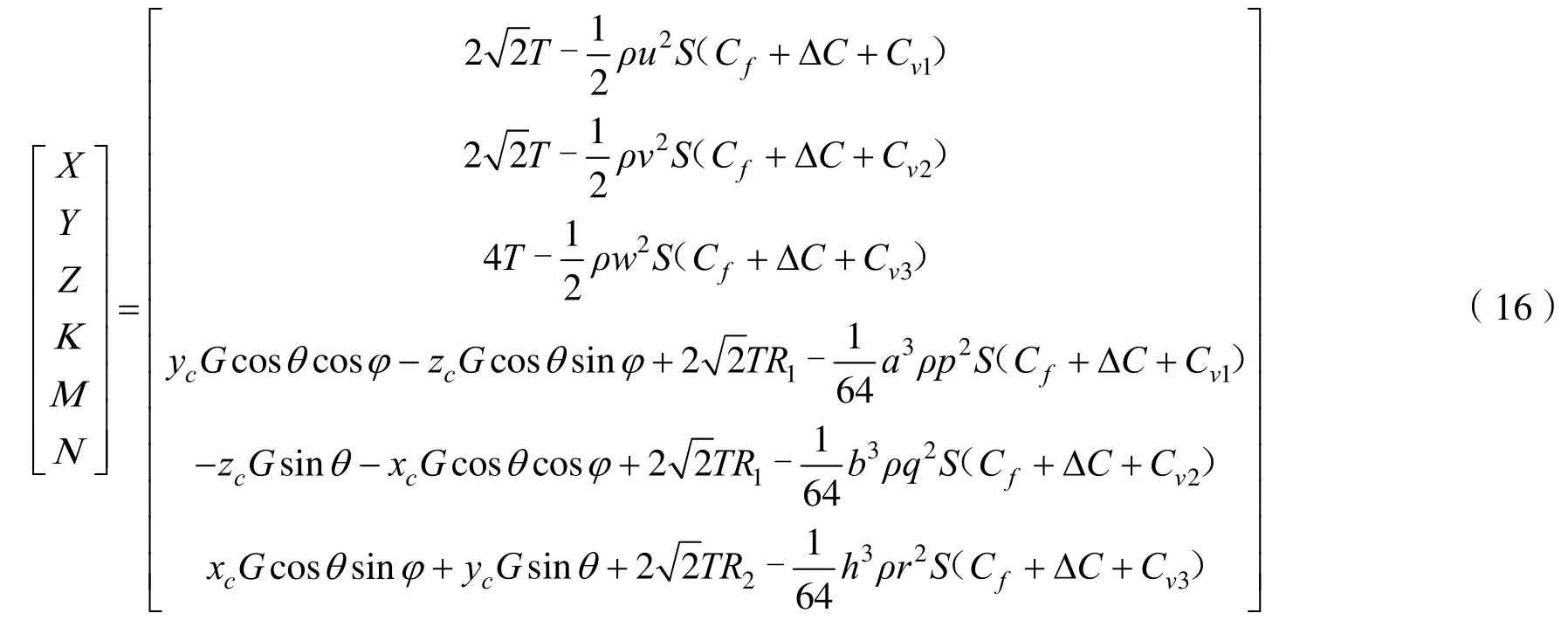
推導可得水下機器人在不計水流的 6個自由度空間運動方程，公式如下。

沿x軸方向前進與后退運動的方程

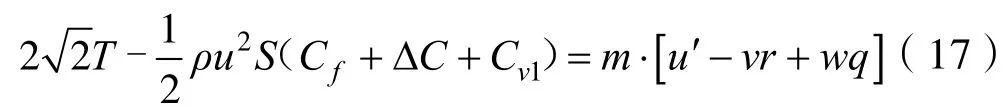
沿y軸方向的左右平移運動方程

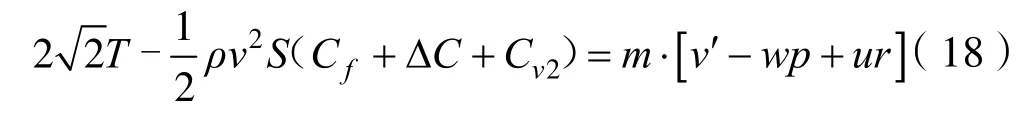
沿z軸方向的垂直上下運動方程

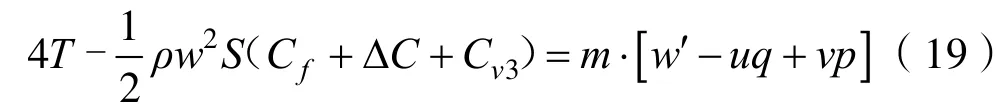
繞x軸旋轉的橫滾運動方程

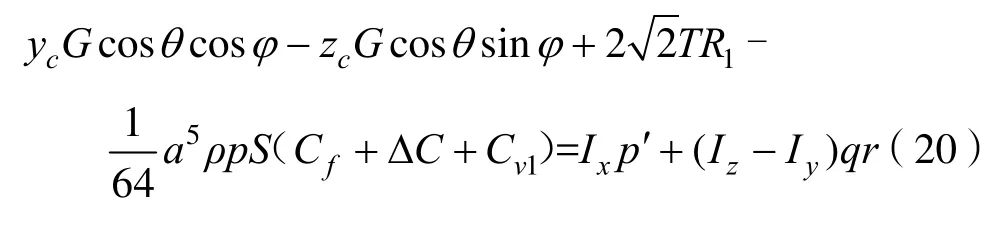
繞y軸旋轉的俯仰運動方程

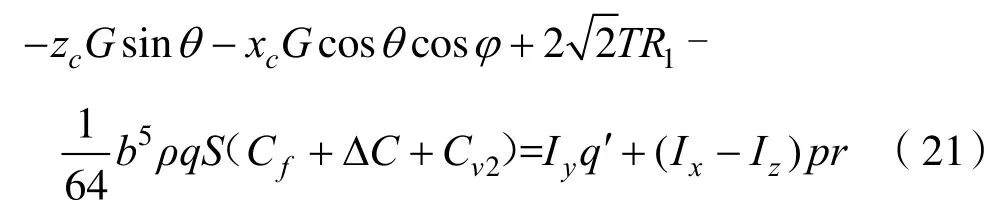
繞z軸旋轉的偏航運動方程

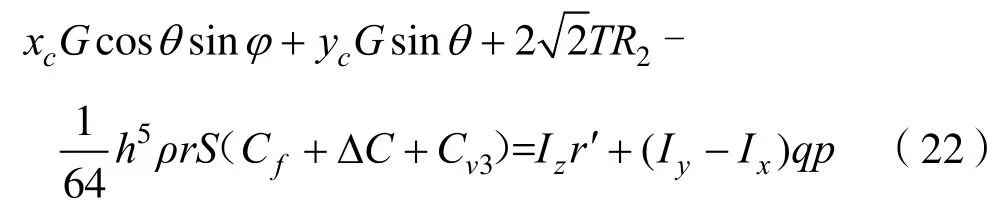
3 運動仿真與性能分析

根據上節中得出的模型，結合該水下機器人及環境的具體參數，可對其運動情況進行建模仿真。

3.1 水平面運動

當水平方向推進器旋轉方向全部相同，使得水下機器人進行前進與后退運動，其速度u隨時間的速度響應如圖2所示。速度u在推力T的作用下慢慢增加，隨后在2.5 s左右達到最大值并保持穩定。當單個推進器T=20 N時，最大速度可達1.9 m/s。

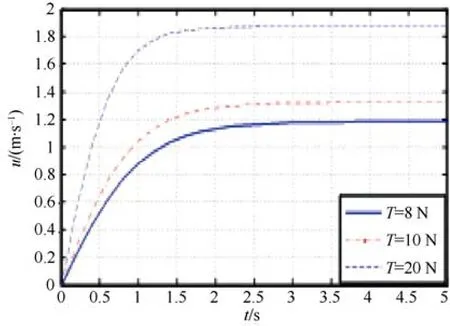
圖2 前進與后退速度響應圖Fig.2 Forward and backward speed response diagram

當水平方向推進器兩對角的 2組推進器旋轉方向不同，同時對角上的 2個推進器旋轉方向相同，使得水下機器人進行左右側移運動，其速度v隨時間的速度響應圖如圖3所示。在水平軸上的點是水下機器人的起點，速度v在推力T的作用下慢慢增加，隨后在2 s左右達到最大值并保持穩定。當單個推進器T=20 N時，最大速度可達1.85 m/s。

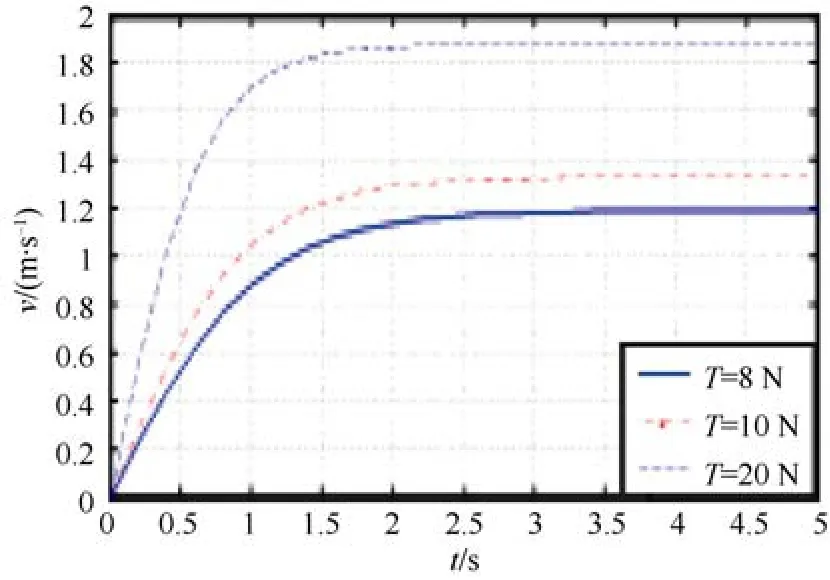
圖3 左右側移速度響應圖Fig.3 Left and right side shift speed response diagram

當水平方向推進器左右 2組推進器旋轉方向不同，同時左右2側的兩個推進器旋轉方向相同，使得水下機器人進行左右轉彎偏航運動，其角速度r隨時間的速度響應如圖4所示。角速度r在推力T的作用下慢慢增加，隨后在6 s左右達到最大值并保持穩定。當單個推進器T=20 N時，最大角速度可達 3o/s。

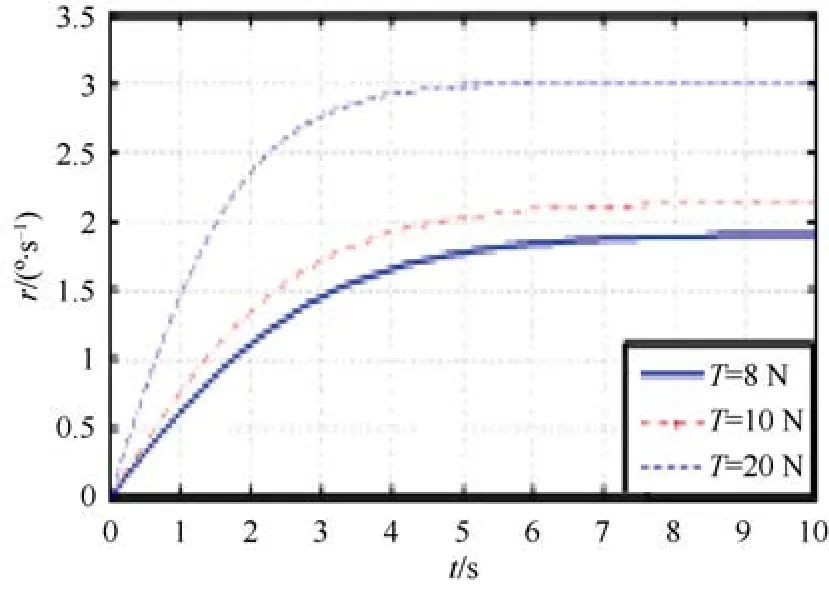
圖4 偏航角速度響應圖Fig.4 Yaw angular velocity response diagram

3.2 縱平面運動

當垂直方向推進器旋轉方向全部相同，使得水下機器人進行上浮與下潛運動，其速度w隨時間的速度響應如圖5所示。速度w在推力T的作用下慢慢增加，隨后在2 s左右達到最大值并保持穩定。當單個推進器T=20 N時，最大速度可達2.25 m/s。

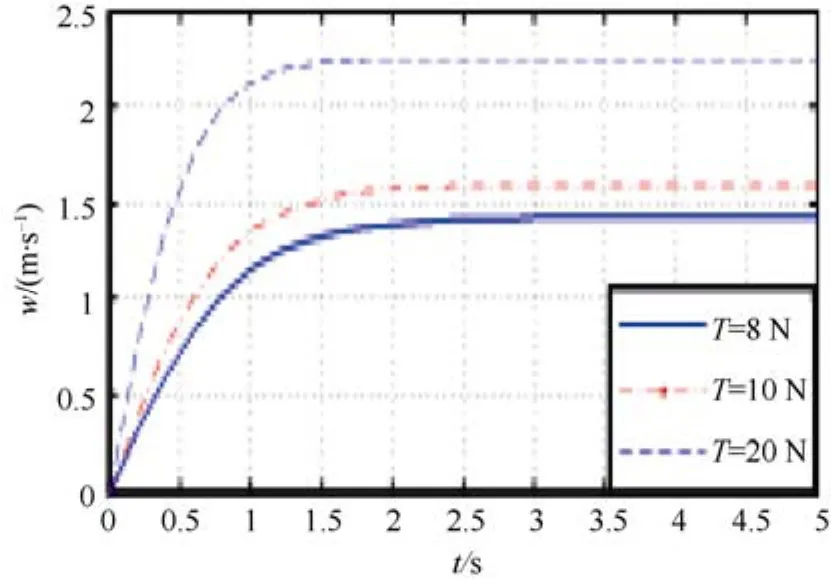
圖5 上浮與下潛速度響應圖Fig.5 Up and down speed response diagram

當垂直方向推進器前后 2組推進器旋轉方向不同，同時前后兩側的2個推進器旋轉方向相同，使得水下機器人進行前后俯仰運動，其角速度q隨時間的速度響應如圖6。角速度q在推力T的作用下慢慢增加，隨后在5 s左右達到最大值并保持穩定。當單個推進器T=20 N時，最大角速度可達13o/s。

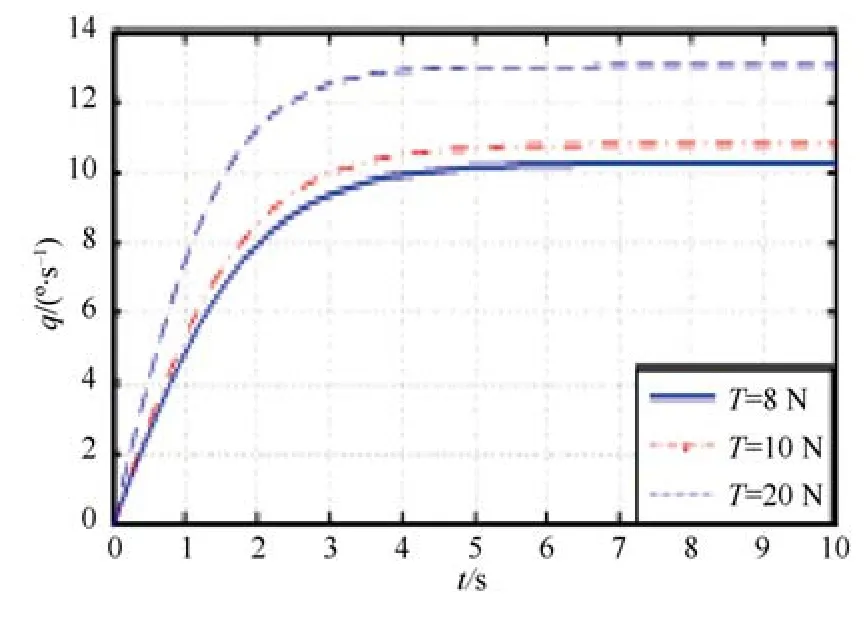
圖6 俯仰角速度響應圖Fig.6 Pitching angular velocity response diagram

3.3 橫滾運動

當垂直方向推進器左右 2組推進器旋轉方向不同，同時左右兩側的2個推進器旋轉方向相同，使得水下機器人進行左右橫滾運動，其角速度p隨時間的速度響應如圖7。角速度p在推力T的作用下慢慢增加，隨后在2 s左右達到最大值并保持穩定。當單個推進器 T=20 N時，最大橫滾角速度可達4.6o/s。

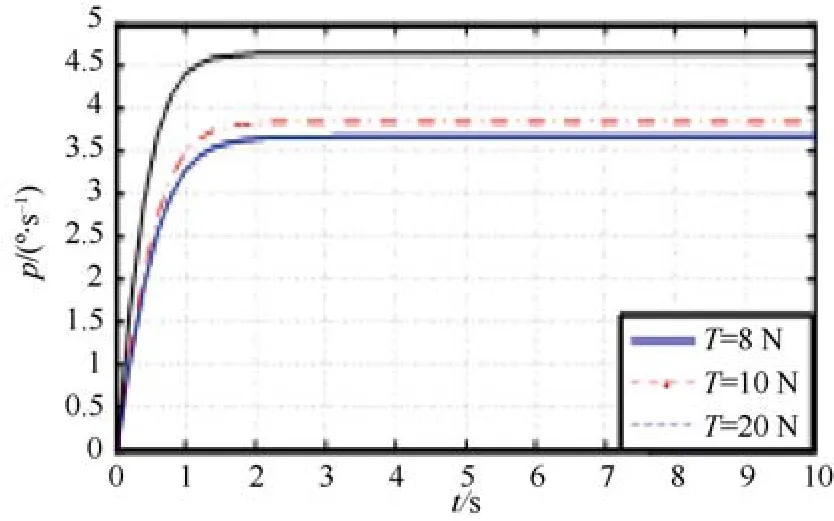
圖7 橫滾角速度響應圖Fig.7 Rolling angular velocity response diagram

4 結束語

本文從受力分析出發，對某型八推進器水下機器人進行了動力學方程建模，得出了其在6個自由度上的運動方程。在此基礎上，對其進行了運動仿真及性能分析，得到了該型水下機器人在6個自由度上的運動性能。通過仿真計算的結果，可以直觀地了解其運動能力，這是進行水下機器人總體性能、彈道、控制和導航系統研究、設計與仿真的基本前提和重要依據。同時由結果可知，該型水下機器人具備多個自由度的運動能力，靈活性高，具備實現多種功能的運動能力基礎。