鋼筋混凝土懸臂梁剪切破壞及尺寸效應律研究

金 瀏，王 濤，杜修力，夏 海

(北京工業大學城市減災與防災防護教育部重點實驗室，北京 100124)

鋼筋混凝土梁的失效模式主要包括彎曲破壞和剪切破壞2種，其中剪切破壞是最為危險的一類，通常表現出明顯的脆性破壞特征。因此，鋼筋混凝土梁的剪切破壞行為存在明顯的尺寸效應現象[1-9]。

眾多試驗研究工作均表明無腹筋鋼筋混凝土梁抗剪強度存在尺寸效應現象。Kani[1]開展了梁高分別為150 mm~1220 mm、幾何相似的無腹筋混凝土梁剪切破壞試驗，Kin和Park[2]開展了梁高分別為170 mm~1000 mm高強鋼筋混凝土無腹筋梁剪切破壞試驗(其中，梁的配筋率為1.0%~4.7%，剪跨比為1.5~6.0)，Chana[3]設計了36根鋼筋混凝土簡支梁(梁高分別為150 mm~750 mm)剪切破壞試驗，Yu等[4]開展了最大梁高為1200 mm的無腹筋混凝土梁剪切破壞試驗。以上試驗結果均表明：無腹筋混凝土梁抗剪強度存在明顯的尺寸效應現象。

雖然無腹筋鋼筋混凝土梁剪切破壞尺寸效應行為已被眾多試驗研究所證實，但由于剪切破壞問題極為復雜，不同學者對機理有不同甚至是相悖的解釋。Collins、Kuchma[5]和Lubell等[6]認為大尺寸構件受剪破壞會出現寬裂縫，這些寬裂縫會減小梁的骨料咬合力，從而使大尺寸梁在破壞時的剪應力降低。他們分析認為腹部裂縫的間距與梁高成正比，并提出了裂縫間距尺寸效應模型。而Ba?ant等[7]認為，裂縫間距尺寸效應模型是不合理的，在最大荷載時，可以忽略斜裂縫上通過骨料咬合作用而傳遞的剪力，尺寸效應與裂縫間距僅部分關聯，大尺寸構件的剪切破壞呈現出接近線彈性斷裂的趨勢。Ba?ant和Kim[8]將斷裂力學理論應用到鋼筋混凝土梁抗剪承載力尺寸效應的研究中，認為產生尺寸效應的根本原因是較寬的斜裂縫使得混凝土中的殘余拉應力減小，同時給出了相對應的尺寸效應系數。Ba?ant的尺寸效應律具有極為明確的理論基礎，在綜合考慮多種因素而進行的統計分析后，表現出了很強的適用性。

對于含有箍筋的混凝土梁，箍筋的存在限制了梁內裂縫的開展，進而使得骨料間的咬合作用增強，因而含有腹筋的鋼筋混凝土梁力學行為更為復雜。眾多學者對含腹筋混凝土梁抗剪承載力尺寸效應的認識仍然存在分歧。Lubell等[6]認為配置設計所要求的最低箍筋率，也能完全消除梁的抗剪強度尺寸效應現象。而Walraven和Lehwalter[9]開展的試驗研究表明：超過最小配箍率的混凝土深梁，其抗剪強度依然表現出了明顯的尺寸效應現象。Yu和Ba?ant[10]的數值結果同樣表明，箍筋的存在僅能削弱梁的抗剪強度尺寸效應，即使梁內配置了很高的配箍率，尺寸效應也不能被完全抑制。Jin等[11]設計了最大梁高為1000 mm，剪跨比為2的鋼筋混凝土懸臂梁在承受低周往復荷載作用下的剪切破壞試驗，試驗結果表明含有腹筋的懸臂梁在循環加載下的名義抗剪強度具有明顯的尺寸效應現象。Bhal[12]的含腹筋混凝土細長梁受剪試驗研究同樣表明了梁的抗剪強度存在明顯的尺寸效應現象。總體來說，腹筋對混凝土梁剪切破壞尺寸效應的影響機制極為復雜，研究者對此問題的認識還遠遠不足，需要開展更為深入的研究工作。

現有的尺寸效應理論，典型的包括Ba?ant[13]斷裂力學理論尺寸效應律、Carpinteri等[14]基于分形理論的尺寸效應律以及Weibull[15]統計尺寸效應律等，均是針對混凝土等脆性材料，采用理論推導及半理論半經驗等手段建立起來的理論公式，它們局限于混凝土材料層次，且僅能體現“結構尺寸”這一因素的大致影響。實際上，對于鋼筋混凝土梁，配箍率、剪跨比等均為影響強度及尺寸效應的重要因素。因此，以上適用于材料層次的尺寸效應理論難以反映構件層次破壞的尺寸效應行為，亦不能體現配箍率及剪跨比對強度尺寸效應的定量影響。

本文采用三維細觀隨機骨料模型，運用數值模擬手段，分析了剪跨比及配箍率對鋼筋混凝土梁剪切破壞尺寸效應行為的影響機制。結合經典的Ba?ant材料層次尺寸效應律，提出了考慮剪跨比及配箍率影響的鋼筋混凝土梁抗剪強度尺寸效應半經驗-半理論公式。

1 鋼筋混凝土懸臂梁三維數值模型

1.1 細觀數值模型的建立

從細觀層次考慮，混凝土可看作是由骨料顆粒、砂漿基質以及兩者間的界面過渡區[16]組成的三相非均質復合材料。參照Du等[17]的工作，將粗骨料顆粒假定為球體，混凝土采用二級配(粗骨料最小等效粒徑為12 mm，最大等效粒徑為30 mm)，骨料體積分數為30%，通過隨機投放的方法將粗骨料顆粒投放到砂漿基質中，并將粗骨料周圍1 mm的薄層設定為界面過渡區，進而生成素混凝土三維細觀模型。將有限元網格在三維結構上進行投影，然后按照各組分在網格中的相對位置判定單元類型，并設置相應的材料屬性。插入鋼筋籠，進而生成鋼筋混凝土懸臂梁三維細觀力學分析模型。為減少模型計算量，提高計算工作效率，混凝土各相組分按照八節點六面體減縮積分單元進行劃分，鋼筋采用梁單元進行離散，網格單元平均尺寸為2 mm。加載方式采用位移控制加載。細觀幾何模型及加載方式如圖1(a)所示。

圖1 鋼筋混凝土懸臂梁三維細觀數值模型Fig.1 3D mesoscopic numerical model of RC cantilever beam

1.2 細觀組分本構關系

通常認為，骨料顆粒強度較高，靜力加載時不產生大變形，因此，將骨料單元力學屬性設為彈性體。對于砂漿基質及界面過渡區，其力學性能采用塑性損傷本構模型[18]來描述，即假定材料的破壞形式主要分為拉伸損傷和壓碎破壞，用各向同性損傷變量描述拉伸損傷和壓縮損傷引起的剛度退化行為，其具體的應力-應變關系為：

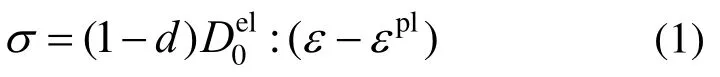
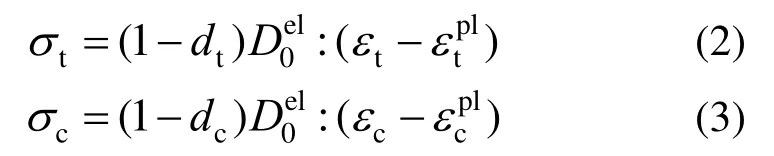
鋼筋視為均質材料，采用理想彈塑性本構模型描述其力學行為。本文采用《混凝土結構設計規范》(GB 50010―2010)[19]推薦的鋼筋-混凝土粘結滑移(τ-s)本構關系模型，即通過設置非線性彈簧單元來描述鋼筋與混凝土之間的粘結滑移行為。彈簧單元的設置形式及其粘結應力τ-滑移量s關系如圖1(b)所示，圖中各關鍵點的確定方法詳見文獻[20]。

1.3 細觀數值模型的驗證

Jin等[11]設計了幾何相似的5組不同尺寸的鋼筋混凝土懸臂梁構件(縱筋率為1.14%，箍筋率為0.14%)，研究了含腹筋懸臂梁在地震循環往復加載下的抗剪破壞行為，并揭示了名義抗剪強度的尺寸效應規律。本文以其中的1組試件作為模擬對象，驗證上文所建立的細觀數值模型的適用性。進而在此基礎上開展了更大尺度的懸臂梁剪切破壞模擬試驗，探究剪跨比和配箍率兩大因素對梁抗剪強度尺寸效應的影響規律。

在Jin等[11]的試驗中，所用混凝土強度等級為C35，實測抗壓強度37.1 MPa；縱筋采用HRB335級鋼筋，箍筋采用HPB235級鋼筋。

混凝土3種細觀組分及鋼筋力學參數如表1所示，包括拉伸/壓縮強度，斷裂能等力學參數。其中：“*”所示的力學參數為實測數據；“^”所示的界面力學參數是通過反復試算確定的界面力學參數[21]。具體的做法是將實際的砂漿基質的力學參數進行不同程度的折減(如70%~85%)，作為界面力學參數的試算值，然后對混凝土立方體試塊(邊長為150 mm)進行反復的壓縮破壞數值模擬試驗，選取最接近實測混凝土抗壓強度的1組數據作為界面力學參數。

表1 混凝土細觀組分及鋼筋力學參數Table 1 Mechanical parameters of the three meso components of concrete and reinforcing bars utilized

在進行大量的反復試算后，發現采用表1中的力學參數時，獲得的混凝土單軸壓縮強度為37.2 MPa，與實測強度37.1 MPa非常接近。因而可認為該界面力學參數選取的合理性。

為驗證上述細觀尺度數值模擬方法的合理性與有效性，結合試驗開展了懸臂梁剪切破壞數值模擬。圖2(a)為試驗結果與模擬結果破壞模式對比圖。在低周往復荷載作用下，試驗梁最終產生X形裂縫，梁的兩側由于受拉而產生了細微裂紋，但破壞時的主裂縫從固定端一側斜向貫通至加載點附近，主裂縫處的混凝土由于受拉嚴重并達到極限拉應變而部分脫落，底部混凝土受壓并達到極限壓應變而脫落，懸臂梁最終破壞。圖2(b)為骨架曲線對比圖。模擬得到的骨架曲線大致形狀及荷載峰值均與試驗結果吻合較好，只有反向加載段的曲線走向與試驗結果有部分偏差。

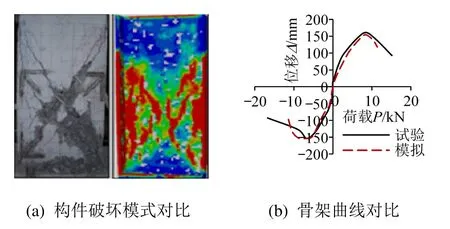
圖2 試驗與模擬結果對比Fig.2 Comparison of the test and simulation results

綜上所述，采用本文介紹的模擬方法在梁的破壞模式及抗剪承載能力等方面均可得到合理的結果，驗證了模型的合理性及準確性。

2 剪跨比對抗剪強度尺寸效應的影響

為研究剪跨比對鋼筋混凝土懸臂梁抗剪強度及其尺寸效應的影響，采用上述方法，設計了剪跨比為1.0、1.5和2.0三組無腹筋懸臂梁單調加載下剪切破壞模擬試驗，其中每組懸臂梁包含4種不同截面尺寸(100 mm×200 mm、200 mm×400 mm、400 mm×800 mm、800 mm×1600 mm)的構件。模型相關幾何參數如表2所示。對于表2的試件名稱，以“CB-1.0-0.0-200”為例，字母“CB”代表Concrete Beam(混凝土梁)；數字“1.0”代表懸臂梁剪跨比λ為1.0；數字“0.0”代表配箍率為0.0%；數字“200”代表懸臂梁橫截面高度為200 mm。因模型數量較多，表2只列出部分試件的幾何參數，其它試件名稱及參數可按命名方式類比得出。

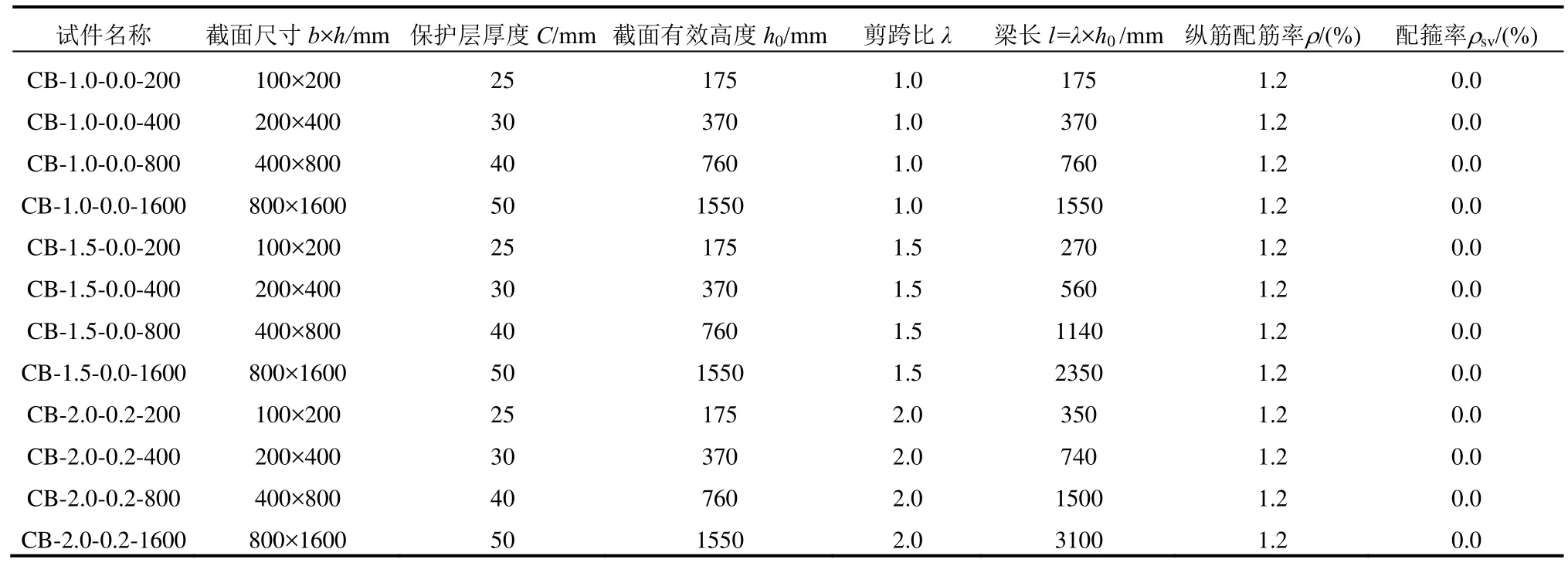
表2 鋼筋混凝土懸臂梁幾何參數Table 2 Geometrical parameters of the RC cantilever beam

2.1 壞模式描述

不同剪跨比(λ=1.0、1.5、2.0)下各無腹筋鋼筋混凝土懸臂梁在單調荷載下最終破壞模式如圖3所示。根據模型最終破壞的形態特點，可以判斷所有試件均為剪切破壞。當剪跨比和梁截面尺寸都較小時，如CB-1.0-0.0-200，梁最終破壞時的主斜裂縫從加載點斜向延伸至固定端底部，混凝土形成多個斜向受壓短柱而被壓碎，具有明顯的斜壓破壞特征。隨著剪跨比及截面尺寸的增大，懸臂梁破壞時有明顯橫向發展的彎曲裂縫。以CB-1.5-0.0-800為例，圖4為該懸臂梁裂縫發展過程圖。加載初期，梁內首先出現橫向發展的彎曲裂縫，隨后裂縫橫向延伸，此階段荷載位移曲線接近直線，梁剛度退化不顯著，處于彈性階段；隨著荷載增大，橫向裂縫開始斜向延伸；荷載進一步增大，新產生的裂縫斜向發展，并與已有斜裂縫逐漸貫通，此時梁剛度退化明顯，荷載逐漸達到峰值；最終梁內形成由加載點到固定端底部的貫通斜裂縫，混凝土梁破壞。

2.2 無腹筋懸臂梁名義抗剪強度及尺寸效應分析

圖5為相同尺寸，不同剪跨比的無腹筋懸臂梁荷載-位移(P-Δ)曲線。加載初期，曲線接近直線，梁剛度基本保持恒定，此時已經有細微裂縫出現；隨后曲線出現一定程度的波動，剛度不穩定退化，此時裂縫開始斜向發展；繼續加載，曲線仍處在上升階段，但隨著裂縫斜向擴展延伸，剛度退化明顯；最終曲線達到峰值后陡降，梁剛度急劇退化，發生明顯的脆性剪切破壞，完全失去承載能力。如圖5所示，隨著剪跨比的增大，梁抗剪承載力明顯降低。小剪跨比(λ=1.0)時，梁的P-Δ曲線在峰值點后下降更為劇烈，表明斜壓破壞相比于剪壓破壞具有更強的脆性特征。

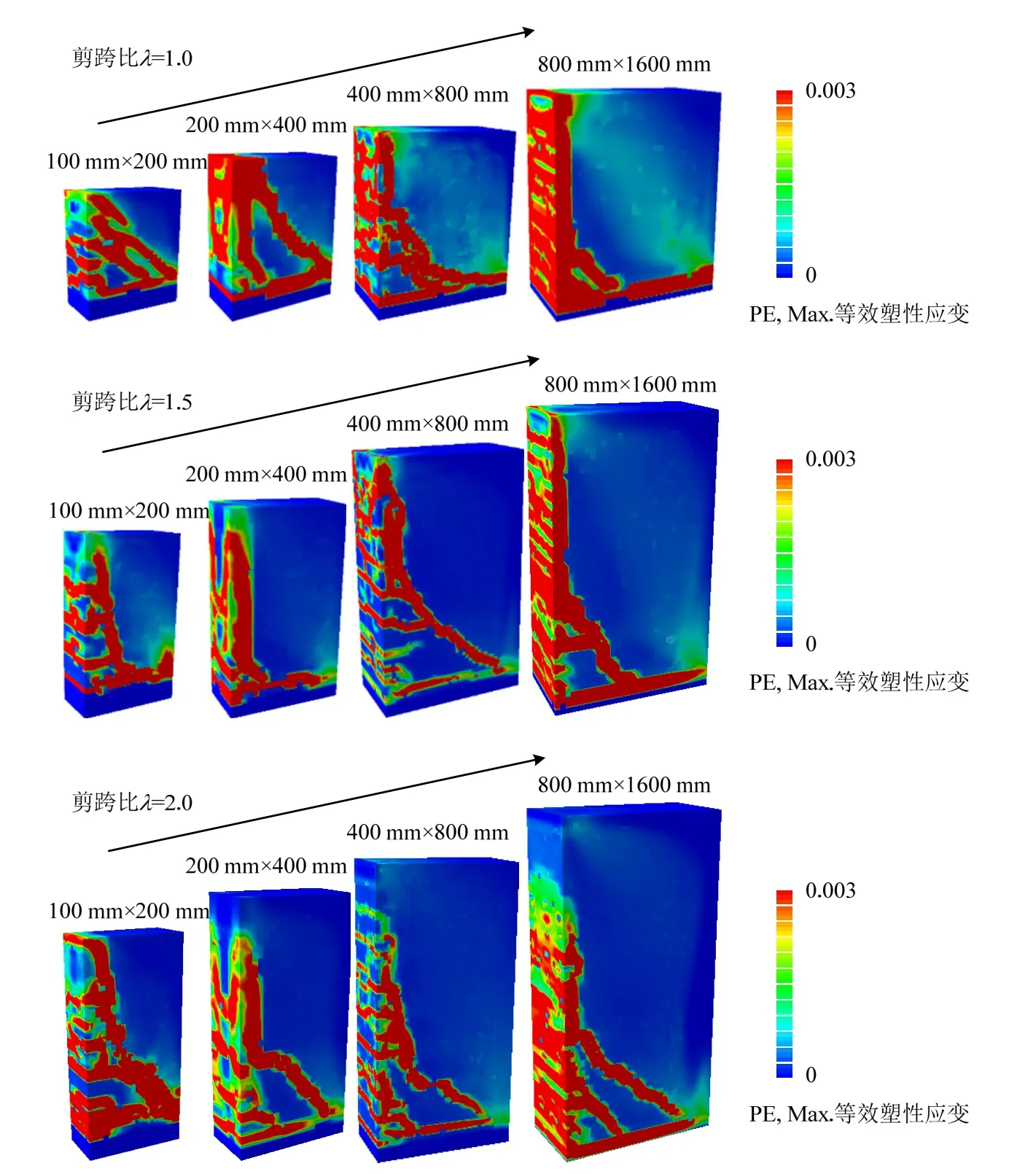
圖3 不同剪跨比不同尺寸懸臂梁最終破壞形態Fig.3 Ultimate failure modes of the cantilever beams with different sizes and different shear span ratios

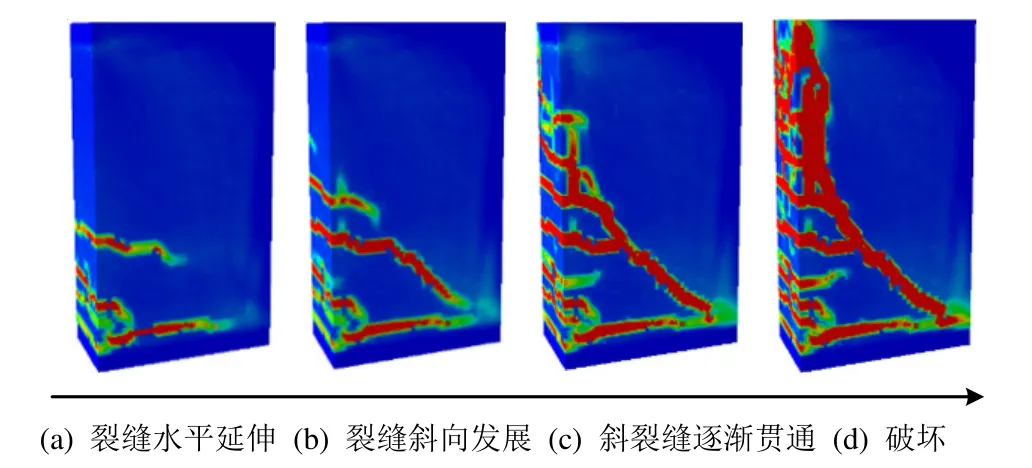
圖4 剪跨比為1.5梁高800 mm懸臂梁裂縫開展過程Fig.4 Crack process of the cantilever beam with a height of 800 mm and a shear span ratio of 1.5

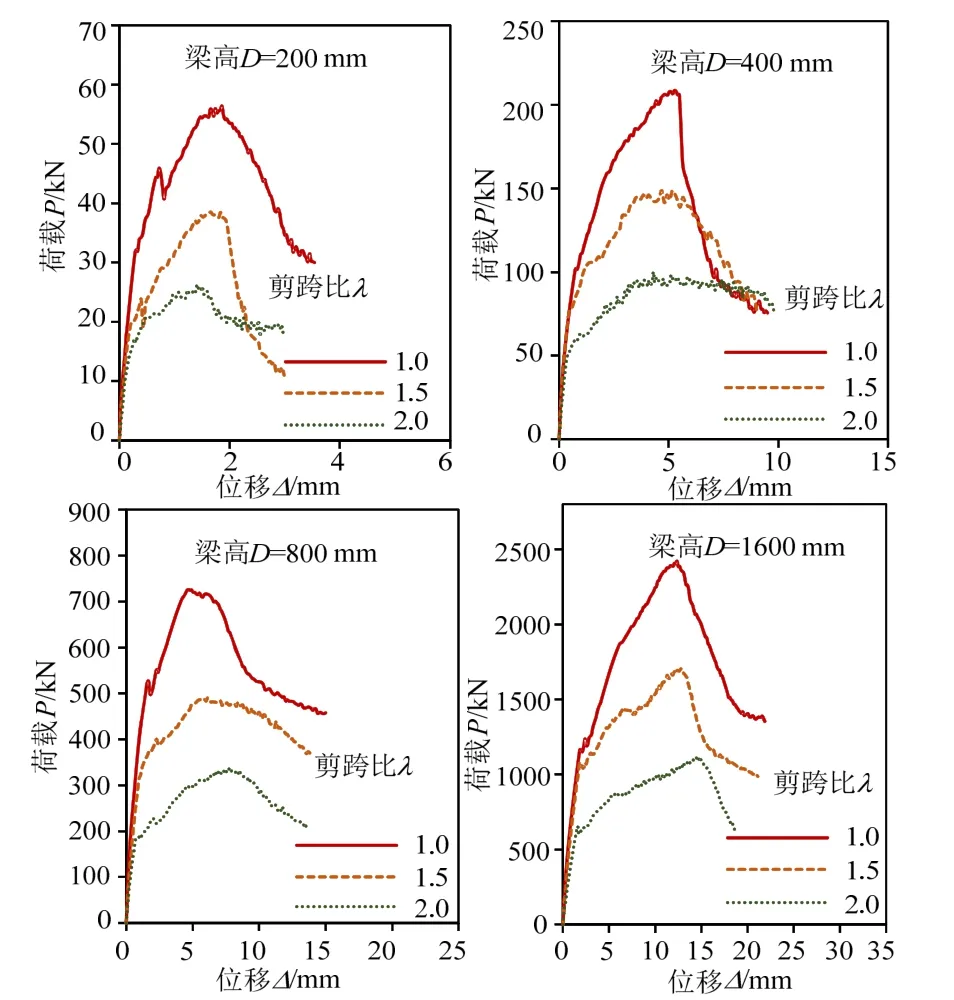
圖5 相同尺寸試件在不同剪跨比下的P-Δ曲線Fig.5 P-Δ curves of specimens of the same size at different shear span ratios

圖6為3種剪跨比下的無腹筋懸臂梁名義抗剪強度隨尺寸的變化趨勢。相同尺寸的懸臂梁，剪跨比越小，名義抗剪強度越大。剪跨比最小(λ=1.0)的梁名義抗剪強度比剪跨比最大(λ=2.0)時提高近50%，說明剪跨比對抗剪強度值有著極為重要的影響。對于相同剪跨比的梁，名義抗剪強度隨尺寸的增大而明顯降低，梁高1600 mm比200 mm的梁名義抗剪強度下降近40%，表現出了明顯的尺寸效應現象。但由于圖6中3條趨勢線基本平行，即不同剪跨比下，懸臂梁的名義抗剪強度隨尺寸下降的趨勢和速度相同，說明剪跨比對尺寸效應的影響較小。

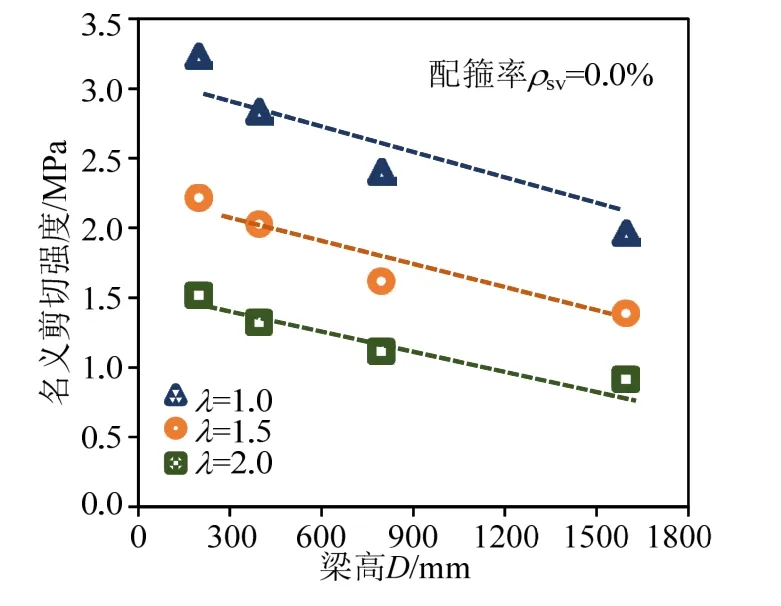
圖6 無腹筋懸臂梁名義抗剪強度Fig.6 Nominal shear strength of cantilever beams without web reinforcement

Ba?ant基于斷裂力學理論提出了適用于混凝土材料的尺寸效應理論公式[13]：

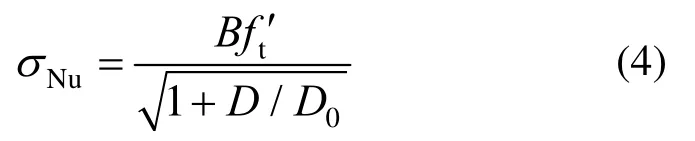
式中：σNu為混凝土構件的名義抗剪強度；B和D0為經驗系數；D為混凝土構件的特征尺寸(這里即為梁截面高度)；為混凝土抗拉強度，這里采用混凝土材料劈拉強度模擬值2.01 MPa。將式(4)轉化為線性方程：

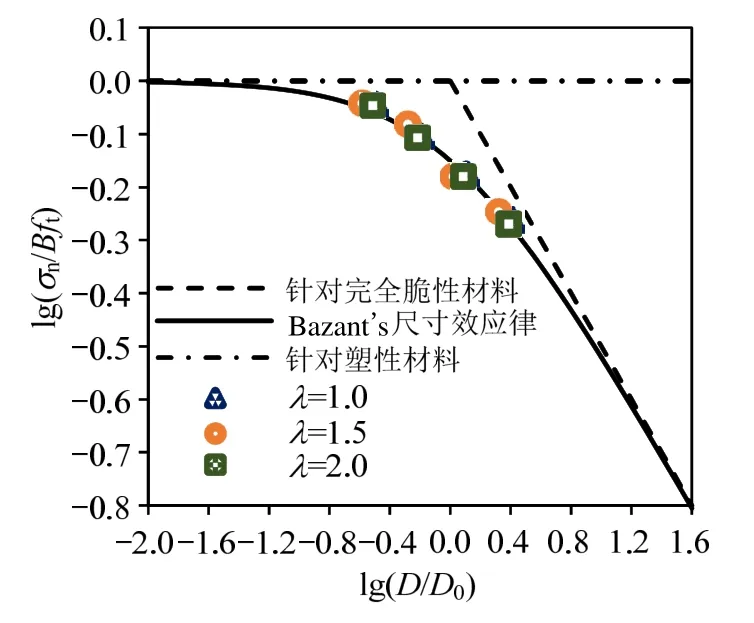
圖7 無腹筋懸臂梁名義抗剪強度尺寸效應擬合Fig.7 Size effect fitting of nominal shear strength of cantilever beams without web reinforcement

3 配箍率對抗剪強度尺寸效應的影響

對于含有腹筋的鋼筋混凝土梁，箍筋一方面可以直接承受剪力，從而提高鋼筋混凝土梁的抗剪承載力；另一方面，箍筋的存在可以限制裂縫開展，提高梁的延性，進而削弱抗剪強度尺寸效應。

基于上述剪跨比為2.0的無腹筋梁(即配箍率為零)剪切破壞模擬試驗，對其配置了0.2%、0.4%、0.6%、0.8%這4種配箍率，進而探究配箍率對鋼筋混凝土懸臂梁抗剪強度及其尺寸效應的影響規律。

3.1 破壞模式描述

配箍率不同，梁的破壞模式有些許差別。圖8給出了0.4%配箍率下不同尺寸懸臂梁的最終破壞模式。對比無腹筋梁，配箍率增大，梁內裂縫橫向開展的更加充分，受拉區混凝土裂縫增多，彎曲破壞現象更加明顯，說明箍筋的存在改善了鋼筋混凝土梁的延性。

3.2 含腹筋懸臂梁抗剪強度及尺寸效應分析

箍筋的存在增大了鋼筋混凝土梁的抗剪承載力，同時改善了混凝土梁的延性，提高了變形能力。圖9給出了相同尺寸，不同配箍率下的懸臂梁荷載-位移(P-Δ)曲線。對比配箍率為0.0%的結果，配有箍筋的梁抗剪承載力都有不同程度的提高，并且曲線在荷載達到峰值點后變得平緩，沒有陡降段，說明梁的剪切延性得到明顯改善。不同配箍率下峰值荷載對應的梁端位移沒有較大變化。

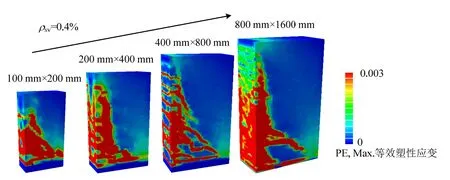
圖8 配箍率為0.4%時不同尺寸懸臂梁最終破壞形態Fig.8 Ultimate failure modes of cantilever beams with different sizes at 0.4% stirrup ratio

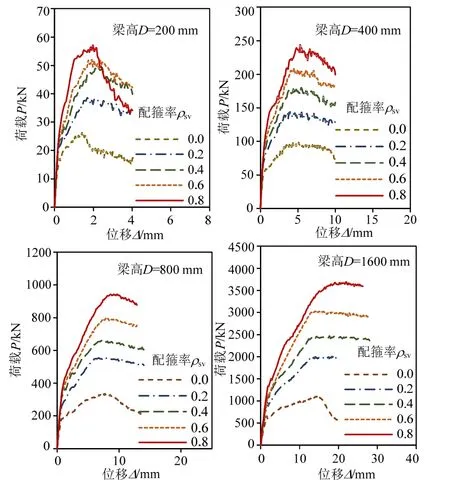
圖9 相同尺寸試件在不同配箍率下P-Δ曲線Fig.9 P-Δ curves of specimens of the same size at different stirrup ratios

圖10為不同配箍率下各懸臂梁的名義抗剪強度及其變化趨勢。配箍率增大使得梁的名義抗剪強度增大，說明箍筋的存在提高了梁的抗剪承載能力。但名義抗剪強度隨著梁高的增大仍有下降趨勢，同樣表現出尺寸效應現象。但隨著配箍率的增大，這種下降趨勢減小，趨勢線逐漸變得平緩，說明箍筋的存在削弱了梁抗剪強度的尺寸效應。即使在很大配箍率下，大尺寸梁的名義抗剪強度仍有下降趨勢，說明配箍率增大僅能削弱尺寸效應，但并不能使尺寸效應完全消除，這與Ba?ant等[10]的結論一致。

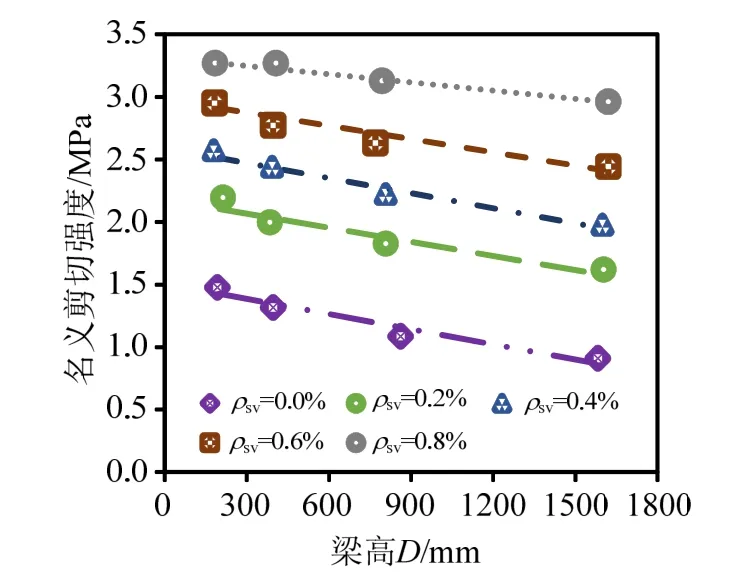
圖10 不同配箍率下懸臂梁名義抗剪強度Fig.10 Nominal shear strength of cantilever beams with different stirrup ratios

4 抗剪強度尺寸效應律

4.1 抗剪強度尺寸效應公式

鋼筋混凝土梁的抗剪承載力V主要由兩部分組成：1) 箍筋直接受剪而承擔的剪力Vsv；2) 無腹筋混凝土梁承受的剪力Vc。因此，梁的抗剪承載力V為：

其中：

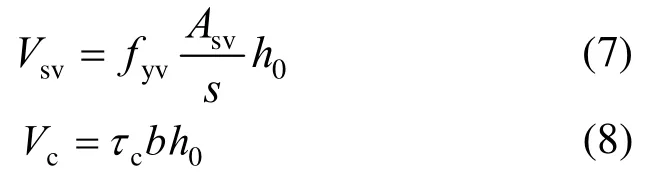
式中：fyv為箍筋抗拉強度設計值；Asv為配置在同一截面內箍筋各肢的全部截面面積；s為沿構件長度方向的箍筋間距；h0為截面有效高度；τc為無腹筋混凝土梁名義抗剪強度；b為梁截面寬度。

鋼筋混凝土梁抗剪承載力分配情況如圖11所示。其中，素混凝土梁所貢獻的承載力Vc(或名義抗剪強度τc)與配箍率、剪跨比及截面尺寸等因素相關，即與尺寸效應有關；而第一部分Vsv為箍筋直接受剪承擔的剪力，與尺寸效應無關。

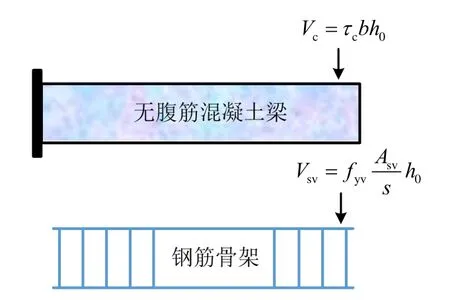
圖11 鋼筋混凝土梁抗剪承載力分配情況示意Fig.11 Indication of shear strength distribution of RC beams

根據第2節的結論，這里首先考慮剪跨比的影響。隨著剪跨比增大，梁抗剪強度呈現出減小趨勢，對此可用剪跨比對抗剪強度的影響系數γ來表征。

由第3節得出的結論，梁內箍筋除直接承受剪力外，同時抑制裂縫開展，改善混凝土梁延性，削弱了抗剪強度尺寸效應。當箍筋對混凝土的約束作用極強(即配箍率極大)時，抗剪強度尺寸效應被極大削弱。這種行為可用配箍率對尺寸效應的削弱系數β來描述。

基于以上兩點認識，在Ba?ant材料層次尺寸效應理論公式的基礎上，考慮剪跨比及配箍率兩種因素對梁抗剪強度及尺寸效應的影響，建立了構件層次上的鋼筋混凝土梁抗剪強度尺寸效應理論公式，如下：

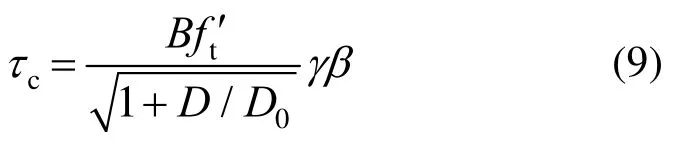
式中：參數γ應為剪跨比的函數；β應為配箍率的函數。因此，這里的τc實際上是考慮了剪跨比、配箍率以及構件尺寸影響下的無腹筋混凝土梁名義抗剪強度。式(9)還反映了構件層次上的鋼筋混凝土梁尺寸效應定量規律與混凝土材料層次尺寸效應規律之間的關聯性。

4.2 尺寸效應公式相關參數確定

4.2.1 剪跨比影響系數γ的確定

我國現行《混凝土結構設計規范》(GB 50010―2010)[19]中鋼筋混凝土梁斜截面受剪承載力Vcs計算公式如下：

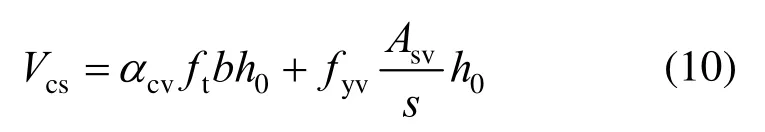
式中：αcv為斜截面混凝土受剪承載力系數，對于一般受彎構件取0.7；對于集中荷載作用下的獨立梁，取αcv為λ為剪跨比。系數αcv實際上是考慮剪跨比對鋼筋混凝土梁抗剪承載力的影響系數。由系數αcv的形式可知，隨著剪跨比的增大，抗剪承載力減小，與前文結論一致。

這里的系數γ借鑒規范公式的形式，考慮γ與剪跨比λ的某種函數形式具有反比形式的關系。對模擬結果進行擬合分析，擬合情況如圖12，得：

需要說明的是，這里的系數γ僅針對本文中所用混凝土情況，其它情況還需進一步討論驗證。

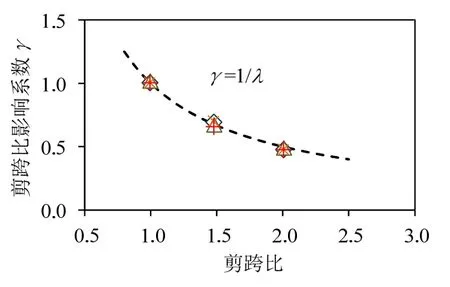
圖12 剪跨比影響系數γ的確定Fig.12 Determination of the weakening coefficient γ

4.2.2 配箍率對尺寸效應削弱系數β的確定

如前文所述，箍筋可以限制裂縫開展，進而改善混凝土梁剪切破壞時的延性，削弱抗剪強度尺寸效應。下面討論配箍率對梁抗剪強度尺寸效應的具體影響。

當ρsv≤ρsv,min時(這里ρsv,min為配箍率下限值)，箍筋對尺寸效應影響作用很小，此時β=1。

當ρsv→∞時，即配箍率很大，此時箍筋對混凝土的約束作用很強，抗剪強度尺寸效應被極大削弱，混凝土梁(構件層次)抗剪強度逐漸趨向于混凝土材料的抗剪強度。這里采用張琦等[22]提出的混凝土抗剪強度與抗拉強度的關系式：

聯立式(9)~式(12)，得到：

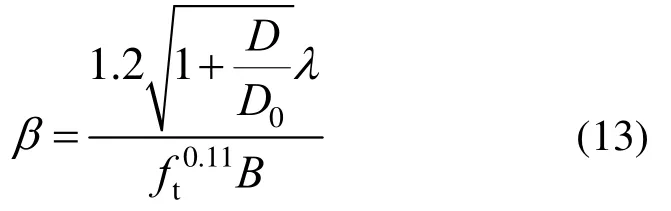
如圖13所示，當ρsv＞ρsv,min時，β成為1條從1開始無限趨向于的非線性變化曲線。這里采用雙曲正切曲線來描述β的變化趨勢，因此可得削弱系數β的表達式為：

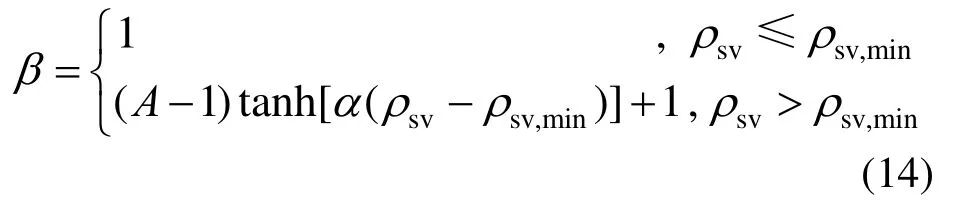
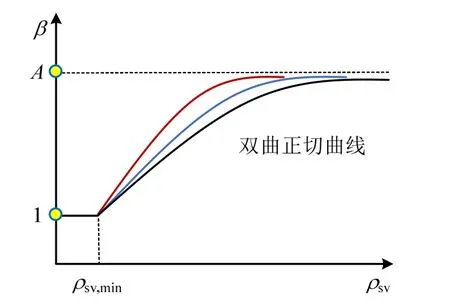
圖13 尺寸效應削弱系數β的確定Fig.13 Determination of the weakening coefficient β

4.3 尺寸效應公式驗證

上述式(9)、式(11)、式(14)需要確定3個參數：B、D0和調節系數α。這里采用剪跨比為1.0的無腹筋懸臂梁模型作為基準試件，模擬結果回歸分析所得到的B=1.802，D0=616。對于調節系數α，可通過與模擬結果的對比擬合來確定。

我國《混凝土結構設計規范》(GB 50010―2010)[19]規定，鋼筋混凝土梁配箍率下限值ρsv,min=0.24ft/fyv，這里ρsv,min取為0.23%。結合所選B和D0，通過數據對比發現，調節系數α在8~12之間時，理論值與模擬結果吻合較好，這里α取10。

在此基礎上，將更多工況下(不同配箍率、不同尺寸)的模擬結果與所提公式的預測值進行對比，如圖14。可以發現所建立的半經驗-半理論公式的預測結果與細觀模擬結果吻合良好，說明了建立的半經驗-半理論公式的合理性和準確性。

另外，這里還搜集了相關的試驗結果來進行對比，圖15即為本文的理論預測值與Jin等[11]及Syroka-Korol等[23]試驗數據之間的對比情況。可以看出二者吻合良好，從而進一步驗證了所提公式的準確性與合理性。

盡管如此，需要說明的是，相關的試驗數據多針對無腹筋或腹筋率較小混凝土梁，因此后續仍需開展大量的試驗工作來驗證本文半經驗-半理論公式的準確性與合理性。

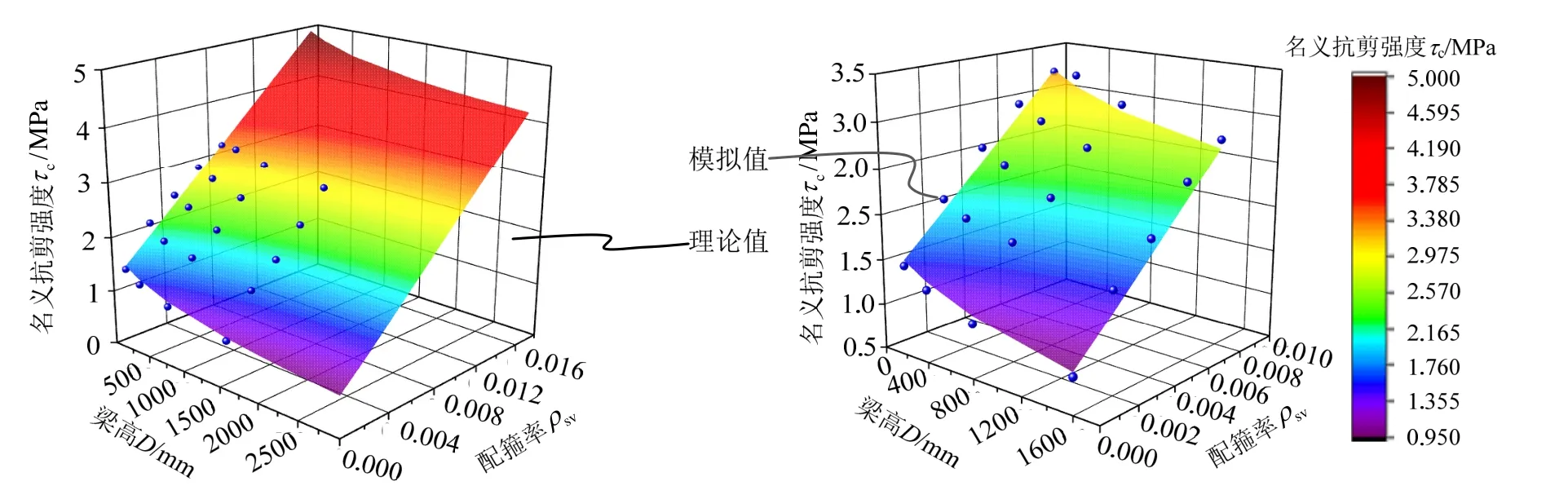
圖14 名義抗剪強度理論值與模擬結果對比Fig.14 Comparisons between the theoretical values and the numerical results

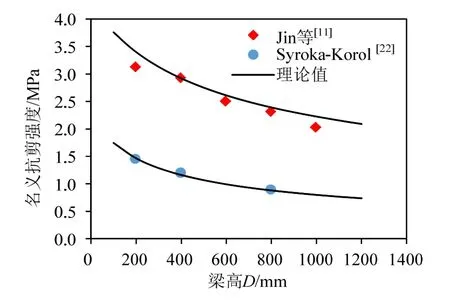
圖15 名義抗剪強度理論值與現有試驗數據對比Fig.15 Comparisons between the theoretical values and the test data

5 結論

本文采用三維細觀數值模擬方法，建立了鋼筋混凝土懸臂梁剪切破壞分析模型，模擬研究了不同剪跨比及不同配箍率下懸臂梁剪切破壞尺寸效應行為，分析了剪跨比和配箍率對梁名義抗剪強度及其尺寸效應的影響機制與規律。進而，在混凝土材料層次經典Ba?ant尺寸效應律的基礎上，提出了可反映剪跨比和配箍率影響的鋼筋混凝土梁剪切強度尺寸效應半經驗-半理論公式。主要結論如下：

(1) 剪跨比對混凝土梁抗剪強度尺寸效應的影響很小，但對抗剪強度值有較大影響，表現為名義抗剪強度隨剪跨比增大而降低。

(2) 梁內箍筋一方面直接承受剪力，增大了梁的抗剪承載力；另一方面通過限制裂縫開展，改善梁的延性，從而削弱了梁抗剪強度尺寸效應，但不能完全抑制抗剪強度尺寸效應行為。

(3) 提出的鋼筋混凝土梁抗剪強度尺寸效應律公式反映了構件層次上的鋼筋混凝土梁尺寸效應定量規律與混凝土材料層次尺寸效應規律之間的關聯性，能很好的描述剪跨比及配箍率對梁抗剪強度尺寸效應行為的影響。

需要說明的是，本文僅討論剪跨比及配箍率對梁抗剪強度尺寸效應的影響，關于混凝土強度等級、加載方式、箍筋間距及箍筋強度等因素對梁抗剪強度尺寸效應的影響將另文研究。