基于微課的微專題設計分析

吳俊英

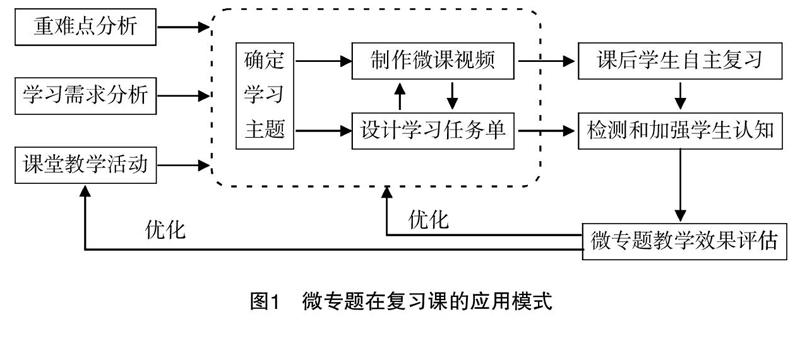
[摘? 要] 文章以空間中平行與垂直為例，闡述微專題在復習課中的應用模式.精選例題及測試題，用微型精細化原則將有關空間的平行與垂直分割成“小切口”的6個微專題，通過例題及變式練習，落實直觀想象素養與數學運算素養的培養，最后給出結合利用微課進行微專題教學實踐的建議.

[關鍵詞] 微課;微專題;平行與垂直;直觀想象

■引言

立體幾何在高考考查中一般占據22分，其題型與題量一般是1個解答題，1～2個選擇題或填空題.高考中立體幾何的解答題常以棱柱或棱錐為載體，解答題一般采用分步設問的方式，常見的兩個考查熱點：一是定性分析，二是定量分析. 其中定性分析，文科主要是以平行、垂直的證明為主;而定量分析，文科試題主要考查表面積、體積的計算. 經過高三一輪復習，學生已經學習了直線、平面平行垂直的判定及其性質，對空間概念有一定的基礎. 但是，絕大多數的學生在定性分析時由于定理條件不清楚，推理的邏輯欠清晰，常造成“會而不全”，導致失分. 同時學生的抽象概括能力、空間想象能力還有待提高，轉化意識還有待加強.

當課堂教學完成后，微專題可以作為課后復習工具應用. 學生在課堂上吸收的知識屬于短時記憶，需要通過及時復習加以鞏固. 微課視頻可以將課堂上教師講解過程再次回放，并可以反復播放，幫助學生復習所學知識，特別是加深對重點、難點知識的認知. 使用時應當提前做好微課視頻，引導學生通過網絡和移動工具開展課后補償性學習，及時復習課堂新授知識，并引導學生抓住零散時間開展學習，進行知識的查漏補缺.

■微專題設計

1. 學習內容與學習目標分析

在點、線、面的位置關系中，直線、平面的位置關系是中心內容，其中直線、平面的平行與垂直尤為重要. 本微專題課擬通過學生在問題探索、應用過程中，對空間直線、平面的平行與垂直進行判定方法的結構性整合，進一步明確直線、平面的平行與垂直之間的內在聯系. 教學重點是直線、平面平行與垂直的判定方法.

本專題采用問題——引導的模式，通過對各學習任務單問題的解決，理清空間直線、平面的平行與垂直證明之間的聯系，復習鞏固、熟練掌握空間直線、平面平行與垂直的判定方法，進一步明確空間直線、平面平行與垂直的相互聯系. 在具體問題的探索中，整合平面平行與垂直的判定方法，從整體上掌握所學的知識并能靈活運用.

學生已具備空間直線、平面平行與垂直判定的基本知識及較為單一的判斷方法，面對問題有一定的思維，能動手一試，但對直線、平面平行與垂直相互之間的聯系的應用意識不強，對問題解決中知識交匯應用和綜合歸納的意識不強.因此確定教學難點為直線、平面平行與垂直的判定方法的結構化整合.

根據以上分析，空間中的平行與垂直總計開發6個課時微專題，每節課提供以下內容：學習任務單、微視頻（對學習任務單進行解析）、在線微檢測.

2. 學習資源及學習測評的設計

微專題1：教學設計“線面平行的證明1——利用平行四邊形進行轉化”.

第一，明確專題指向，直擊思路方法.

教師小結空間平行的證明中常見的方法.

設計意圖：開門見山，進行方法歸納.

第二，精選典型例題，煉思路揭本質.

學習任務單（2016年高考全國Ⅲ卷，文科19題節選）：

如圖2，四棱錐P-ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M為線段AD上一點，AM=2MD，N為PC的中點.

①證明：MN∥平面PAB;

②略.

解題思路簡析：

法一（利用線線平行）：取BP的中點T，可證四邊形AMNT是平行四邊形，進而得到MN∥平面PAB.

法二（利用面面平行）：取BC的中點Q，連接MQ，NQ，可證平面MNQ∥平面PAB，進而得到MN∥平面PAB.

設計意圖：以高考真題吸引學生的學習興趣. 本題較為簡單，通過本題鞏固證明線面平行常見的兩個轉化思路.小專題微課的例題應該具有基礎性、針對性、典型性和研究性. 例題的選擇必須針對重點內容，鞏固“雙基”，貼近學生的“最近發展區”，不要過于追求難度.

第三，精選變式訓練，促進技能形成.

在線微檢測：如圖4，在直角梯形ABCD中，AB∥CD，AB⊥AD，且AB=AD=■CD=1.現以AD為一邊向梯形外作正方形ADEF，然后沿邊AD將正方形ADEF翻折，使平面ADEF與平面ABCD垂直，M為ED的中點，如圖5. 求證：AM∥平面BEC.

選題分析：本題的解題思路和例題相似.

設計意圖：基本技能的掌握必須通過變式練習才可能內化鞏固完成，練習是學生形成技能的有效途徑.利用變式訓練可以讓學生把握問題的本質特征和解題的核心方法，加深對問題的理解，變套路為新式，從模仿到創新.

第四，自主小結方法，反思領悟提高.

學生自主小結本節課的方法，反思內化.

設計意圖：反思例題、訓練題，感悟出運用平行四邊形轉換證明平行的方法是解題的要領和注意事項，讓學生的認識更明確到位.

微專題2：教學設計“線面平行的證明2——逆用平行線分線段成比例定理”.

第一，明確專題指向，直擊思路方法.

第二，精選典型例題，煉思路揭本質.

學習任務單（2017年3月福州市質檢節選）：

如圖6，在等腰梯形PDCB中，PB∥DC，PB=3，DC=1，∠DPB=45°，DA⊥PB于A. 將△PAD沿AD折起，構成如圖7所示的四棱錐P-ABCD，點M在棱PB上，且PM=■MB.

①求證：PD∥平面MAC;

②略.

解題思路簡析：逆用“平行線分線段成比例定理”（利用線線平行）：連接BD交AC于點O，連接OM，可證得PD∥OM，進而得到PD∥平面MAC.

第三，精選變式訓練，促進技能形成.

在線微檢測：如圖8，在四棱錐P-ABCD中，AD∥BC，且BC=2AD，AD⊥CD，PB⊥CD，點E在棱PD上，且PE=2ED.求證：PB∥平面AEC.

選題分析：本題的解題思路和例題相似.

第四，自主小結方法，反思領悟提高.

微專題3：教學設計“線面平行的證明3——利用三角形的中位線”.

第一，明確專題指向，直擊思路方法.

第二，精選典型例題，煉思路揭本質.

學習任務單（2018年高考全國Ⅲ卷，文科19題節選）：

如圖9，矩形ABCD所在平面與半圓弧■所在平面垂直，M是■上異于C，D的點.

①略;

②在線段AM上是否存在點P，使得MC∥平面PBD？說明理由.

解題思路簡析：利用三角形的中位線進行平行轉化：當P為AM的中點時，MC∥平面PBD.

第三，精選變式訓練，促進技能形成.

在線微檢測（2016年高考四川卷，理科18題節選）：

如圖10，在四棱錐P-ABCD中，AD∥BC，∠ADC=∠PAB=90°，BC=CD=■AD，E為棱AD的中點，異面直線PA與CD所成的角為90°.

①在平面PAB內找一點M，使得直線CM∥平面PBE，并說明理由;

②略.

解題思路簡析：在梯形ABCD中，AB與CD不平行. 延長AB，DC，相交于點M（M∈平面PAB），點M即為所求的一個點. （說明：延長AP至點N，使得AP=PN，可證得平面PBE∥平面DMN，則所找的點可以是直線MN上任意一點）.

第四，自主小結方法，反思領悟提高.

設計說明：可以發現利用線線平行證明線面平行是其中的關鍵題型，而平面中證明線線平行的常用方法有：利用平行四邊形的性質（微專題1），逆用“平行線分線段成比例定理”（微專題2），利用“中位線定理”（微專題3），其中微專題1和微專題3也可以先證明面面平行得到線面平行.這三個專題的難度逐漸遞增，供不同情況的學生自主選擇用于課后鞏固，在題目的選擇上，盡量選擇高考題引起學生重視.

微專題4：教學設計“垂直的轉化”.

第一，明確專題指向，直擊思路方法.

第二，精選典型例題，煉思路揭本質.

學習任務單（2017年全國高考Ⅰ卷，文科18題）：

如圖12，在四棱錐P-ABCD中，AB∥CD，且∠BAP=∠CDP=90°.

①證明：平面PAB⊥平面PAD;

②若PA=PD=AB=DC，∠APD=90°，且四棱錐P-ABCD的體積為■，求該四棱錐的側面積.

解題思路簡析：①由條件得AB⊥PD，AB⊥PA，從而AB⊥平面PAD，進而得到平面PAB⊥平面PAD.

②在平面PAD內作PE⊥AD，垂足為E. 由①知，AB⊥平面⊥PAD，故AB⊥PE，可得PE⊥平面ABCD. 可得四棱錐P-ABCD的側面積為6+2■.

第三，精選變式訓練，促進技能形成.

在線微檢測（2015年全國高考Ⅰ卷，文科18題）：

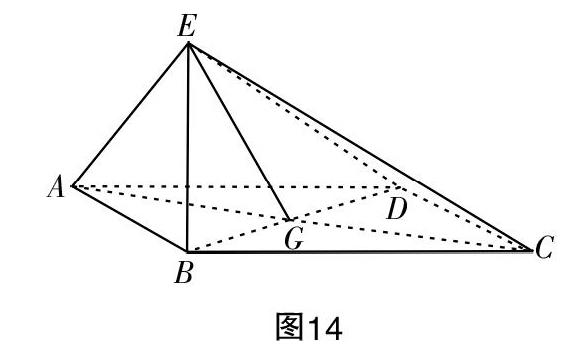
如圖14，四邊形ABCD為菱形，G為AC與BD交點，BE⊥平面ABCD.

①證明：平面AEC⊥平面BED;

②若∠ABC=120°，AE⊥EC，三棱錐E-ACD的體積為■，求該三棱錐的側面積.

解題思路簡析：①先證AC⊥平面BED，再得到平面AEC⊥平面BED. ②三棱錐E-ACD的側面積為3+2■.

第四，自主小結方法，反思領悟提高.

微專題5：教學設計“垂直的證明”.

第一，明確專題指向，直擊思路方法.

第二，精選典型例題，煉思路揭本質.

學習任務單（2014年全國高考Ⅰ卷，文科19題）：

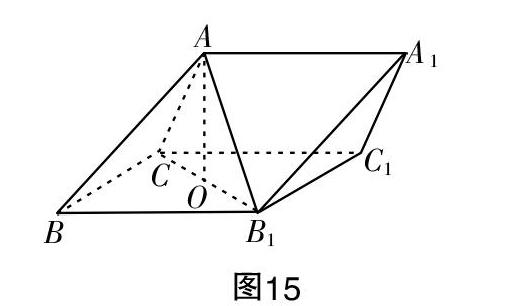
如圖15，三棱柱ABC-A1B1C1中，側面BB1C1C為菱形，B1C的中點為O，且AO⊥平面BB1C1C.

①證明：B1C⊥AB;

②若AC⊥AB1，∠CBB1=60°，求三棱柱ABC-A1B1C1的高.

解題思路簡析：①先證B1C⊥平面ABO，再得到B1C⊥AB.②三棱柱ABC-A1B1C1的高為■.

第三，精選變式訓練，促進技能形成.

在線微檢測（2013年高考全國Ⅰ卷，文科19題）：

如圖16，三棱柱ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°.

①證明：AB⊥A1C;

②若AB=CB=2，A1C=■，求三棱柱ABC-A1B1C1的體積.

解題思路簡析：①取AB的中點O，連接OC，OA1，先證AB⊥平面OA1C，再得到AB⊥A1C. ②先證OA1⊥平面ABC，所以OA1為棱柱ABC-A1B1C1的高，又△ABC的面積S△ABC=■，所以三棱柱ABC-A1B1C1的體積V=S△ABC×OA1=3.

第四，自主小結方法，反思領悟提高.

微專題6：教學設計“垂直的綜合應用”.

第一，明確專題指向，直擊思路方法.

第二，精選典型例題，煉思路揭本質.

學習任務單（2016年全國卷Ⅰ，文科18題）：

如圖17，已知正三棱錐P-ABC的側面是直角三角形，PA=6，頂點P在平面ABC內的正投影為點D，D在平面PAB內的正投影為點E，連接PE并延長交AB于點G.

①證明：G是AB的中點;

②在圖中作出點E在平面PAC內的正投影F（說明作法及理由），并求四面體PDEF的體積.

解題思路簡析：①利用線面垂直與線線垂直的相互轉化以及等腰三角形“三線合一”證明. ②V=■.

第三，精選變式訓練，促進技能形成.

在線微檢測（2018年高考全國卷Ⅱ，文科19題）：

如圖19，在三棱錐P-ABC中，AB=BC=2■，PA=PB=PC=AC=4，O為AC的中點.

①證明：PO⊥平面ABC;

②若點M在棱BC上，且MC=2MB，求點C到平面POM的距離.

解題思路簡析：①連接OB，先證OP⊥OB，又OP⊥AC，再推出PO⊥平面ABC.②點C到平面POM的距離為■.

第四，自主小結方法，反思領悟提高.

設計說明：本設計從學生的學習起點出發，以學生為中心，精選例題及測試題，用微型精細化原則將有關空間的平行與垂直分割成“小切口”的6個微專題，每個微專題解決一個問題，每節課充分考慮學生的認知負荷，適度適量鞏固已有知識和方法.

■微專題開發

微專題開發中的微課視頻制作是一個系統工作，一般從以下幾個環節逐步展開：確定學習內容——撰寫教學設計——制作PPT——錄制微課視頻——優化微課視頻——開發配套資源——上傳和管理微課視頻. 其中微課視頻制作是微專題開發的重要環節，本研究用Camtasia Studio軟件錄制微課視頻. Camtasia Studio是一種專業視頻錄制和編輯軟件，錄制完視頻可以基于時間軸進行編輯，如字幕、貼標簽、畫中畫、媒體庫、特效場景變化、畫外音和主題編輯等，支持多種源文件格式及輸出格式，使用方便，簡單易懂. 錄制微課視頻時，Camtasia Studio會一起錄制所選定的屏幕畫面和講授者的聲音.錄制視頻中教師可充分利用信息技術分析題目，比如借助幾何圖霸動態展示變化過程.

微課視頻制作完成后可發布在公共學習平臺如班級QQ群或微信公眾號上，由學生課后自主學習，再收集學生的作業進行評價和反饋優化微專題資源.

■微專題教學實施建議

（1）考慮到學生的直觀想象水平不一，作為課外學習的一種方法就是制作合適的微課以供學生自學鞏固.通過動態的形式給學生展示圖形的變化，演示各種截面、各種展開圖、不同觀察角度的動畫. 在初學階段可以多借助實物觀察去體會，初步培養學生的空間感覺;后續階段主要是引導學生通過解決空間位置關系的證明以及根據位置關系的轉化解決一些空間角、空間距離、空間最值等問題. 在大量的自身體驗之后獲得經驗，從而發展直觀想象素養. 針對比較復雜的綜合性問題，可采取分層次的方式逐一突破，化整為零;也可細分為某一些微專題，再整合成一個整體. 因此教師可以利用微專題為學生鋪設臺階逐步提升直觀想象素養.

（2）加強現代教育技術與學科教學的融合. 利用信息技術多媒體輔助教學，比如幾何畫板、幾何圖霸、希沃白板等多媒體技術演示動圖讓學生體會空間關系. “動則悅，靜則思”. 在立體幾何教學中可以讓學生在三維動態中沉浸體驗，在直觀圖注視上寧靜思考.比如空間幾何體的不同視角的動態展示，三視圖與直觀圖的轉換過程，以及平面圖形的翻折與展開問題，借助信息技術動態演示，能便捷直觀地了解圖形的特點.

（3）微課的優點是主題突出、時長較短，便于學生利用零碎時間針對自身的疑難問題進行自主學習，能夠更好地滿足學生的不同學習需求，作為課堂的延續可以給課堂教學擴容，提高學生的自學能力，實現效益最大化. 微課不同于文本，能從視聽角度給學生不一樣的刺激，可視，共享，儲存方便，借助網絡突破時間、空間的局限，學生可以更自由地把握學習時間，對重點、難點的問題可以反復觀看，也可以自主選擇薄弱知識或題型總結的微課反復觀看.

總之，應合理設置微專題幫助學生突破學習難點并鞏固重點. 積極有效地將微課的直觀和微專題的短平快、高效簡潔的特點結合起來，發揮二者“因微而準、因微而細、因微而深”等優勢.