向量法在求解幾何問題中的應用

摘?要：向量是建立代數、函數、幾何問題之間聯系的紐帶，作為一種解題方法在簡化相應問題、提升解題效率上非常實用，文章主要探討向量法在幾何命題、三角函數、不等式以及動點軌跡四個方面的應用，最后給出了在解析幾何教學中的幾點建議。

關鍵詞：向量法;代數化;動點軌跡;Matlab軟件

中圖分類號：O182?文獻標識碼：A

解析幾何是數學專業的基礎課，可以說是其他數學課程的基礎，是高等數學類課程的基石。線性代數，數學分析，常微分方程等課程的學習都離不開解析幾何的基本知識及研究方法。其基本思想是用代數的方法來研究幾何，數學家笛卡兒曾說過：一切問題最終都可以轉化為數學問題，一切問題可轉化為代數問題進行研究，雖然這種說法過于絕對，但是很好地說明了用代數中的方法去研究幾何問題的重要性。為了把代數里涉及的運算引進到幾何中，最根本的做法就是設法把空間的幾何結構有系統的代數化、數量化。

幾何中最基本的單位是“點”，點成線、線成面、面成體，而代數中最基本的單位是“數”，要建立幾何與代數之間的關系，就需要建立“點”與“數”之間的關系，即借助空間坐標系來實現[1]。

向量是一個既有大小又有方向的矢量，通過直角坐標系可以將向量的分量分別給出，因此在研究幾何問題中起著重要的作用。本文主要介紹利用向量求解四類幾何問題。

一、向量方法在幾何命題證明中的應用

傳統的幾何命題都是利用已知條件之間的各種變換和構造輔助線來證明，這種方法往往復雜，如果找不到隱含的信息，則無從下手，但是利用向量法卻事半功倍。

例1：利用向量法證明四面體對邊中點的連線交于一點且互相平分。

二、向量法在三角函數中的應用（正弦、余弦定理）

正弦、余弦定理的證明方法有很多[2-3]，比如做輔助線和外接圓，在高中對于學生來說是非常困難的，證明過程復雜、懊悔難懂，一般情況下只有記憶公式沒有理解，在大學的學習中講解了向量的數量積和向量積之后，作為向量的應用外拓，利用向量法證明，學生理解得更透徹，進而對學習向量法產生興趣。

三、向量法在不等式中的應用

柯西——施瓦茲不等式有著非常廣泛的應用，如求函數極值、求解方程、求解三角與幾何問題等方面，證明方法有直接法和三角函數變換證明[4]，構造二次函數法、歸納法、配方法[5]等，向量法證明相對于上述方法更簡單易懂。

四、向量方法在動點軌跡中的應用

例4：把一根線繞在一個固定的圓周上，將線頭拉緊后向反方向旋轉，以把線從圓周上解放出來，使得放出來的部分成為圓的切線，求線頭的軌跡方程。

分析：若將線頭的軌跡方程以普通方程的形式表示，顯然是非常困難且不容易求解的，并且軌跡方程不唯一，但是如果利用向量法來求解動點的軌跡方程，是比較簡單的，只需要理解線頭動之前和動之后的向量關系，那么求解過程簡單直接，降低了問題的難度。

這種曲線叫做圓的漸伸線或者切展線，在工業上常被稱作齒輪曲線[6]。利用向量的方法求解類似的問題，如內旋輪線、外旋輪線等問題的動點軌跡亦是非常簡便的。

在解析幾何教學中筆者有以下三點建議：

一是解析幾何是一門比較抽象的課程，課前應給學生提供相應的學習材料，如慕課資源，課中講解應啟發式的指導學生學習，使學生將高中知識與大學知識銜接起來，而不是脫節;

二是解析幾何中有很多的運算，包括向量的運算和直線、平面的方程求解、直線與平面之間的關系等，在學習的過程中應注重學生計算能力的培養，避免出現上課聽著會考試不會的情況發生;

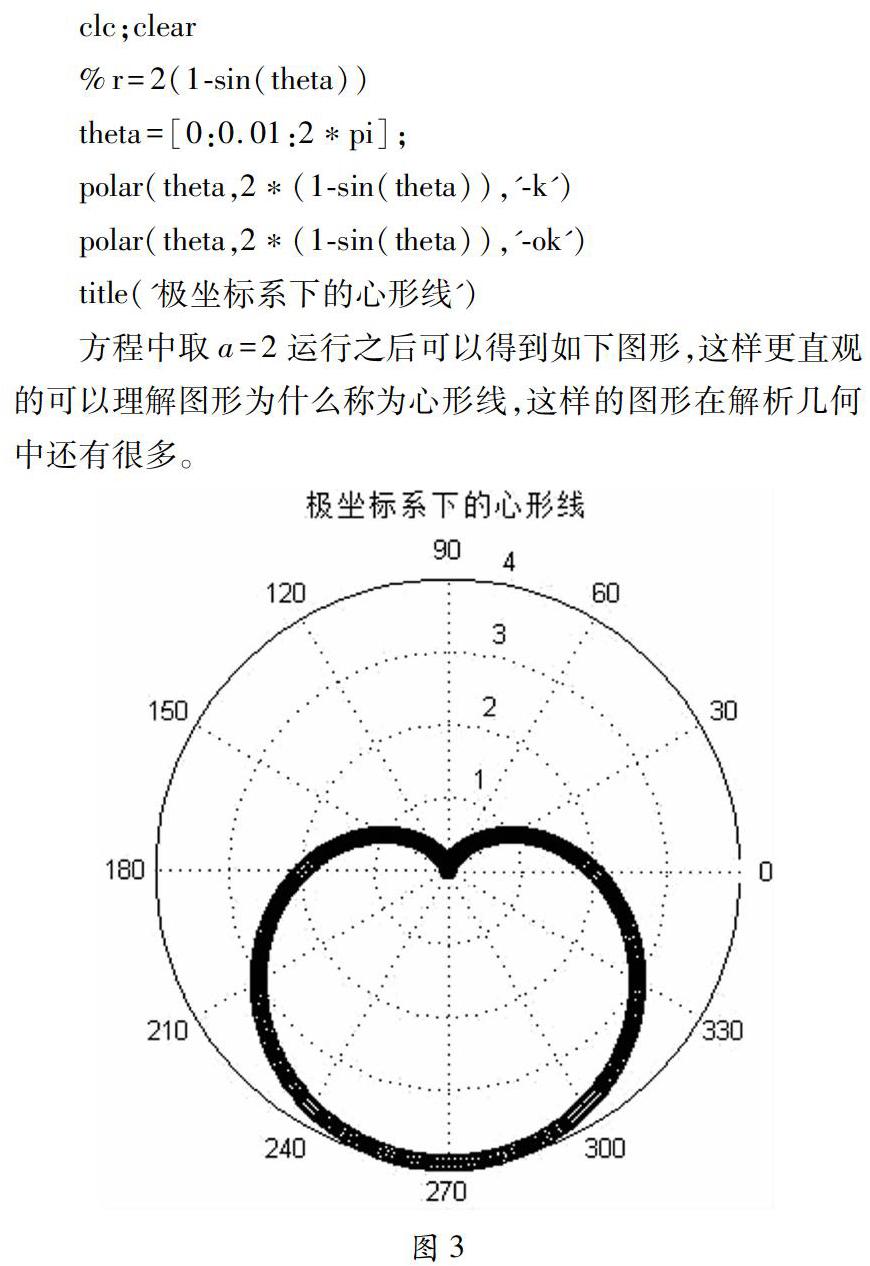
三是學生對于空間中的幾何圖形比較陌生，在上課的時候鍛煉學生數形結合的能力，比如在空間中，方程x2+y2=1代表圓柱，學生第一反應是圓，因此在平時的教學活動中應適當的利用Matlab軟件演示一些幾何圖形，這樣學生容易理解、記憶深刻，而且在無形中向學生介紹了Matlab軟件，這對學生后期的學習奠定了基礎。比如心形線極坐標方程r=a（1-sinθ），a是常數。代碼為：

clc;clear

%r=2（1-sin（theta））

theta=[0：0.01：2*pi];

polar（theta，2*（1-sin（theta）），'-k'）

polar（theta，2*（1-sin（theta）），'-ok'）

title（'極坐標系下的心形線'）

方程中取a=2運行之后可以得到如下圖形，這樣更直觀的可以理解圖形為什么稱為心形線，這樣的圖形在解析幾何中還有很多。

五、結語

以上是向量法在四類問題中的應用以及在教學中的三點建議，當然向量法還有很多應用，比如求解直線方程，求解平面方程，求解定比分點問題等等，在此不一一列舉。向量法為求解上述問題提供了一種新途徑，使得解題思路簡單，化難為易，事半功倍。

參考文獻：

[1]滕吉紅，等.淺析高等數學中蘊含的思維觀和方法論[J].高等數學研究，2020，23（4）：124-127.

[2]趙冬梅.正弦定理、余弦定理的證明方法探究[J].西北成人教育學報，2012，6，137-140.

[3]宋現印.深入應用領域，探討向量解法[J].數學教學通訊，2019，10，78-79.

[4]龔加安.柯西不等式的證明及幾何解釋[J].讀與寫雜志，2018，15（12）：34-35.

[5]黃韜，顧華強.柯西不等式的證明與應用.數學學習與研究，2018（3）：108-109.

[6]呂林根，許子道.解析幾何（第四版）[M].北京：高等教育出版社，2006.

作者簡介：蘇曉璐（1989—?），女，回族，寧夏人，碩士，助教，研究方向：偏微分方程數值解法。