基于神經網絡觀測器的水下拖體輸出反饋姿態控制

井安言， 佘湖清

(宜昌測試技術研究所, 湖北 宜昌 443003)

0 引言

21世紀是海洋的世紀，人類對于海洋的探索永不停歇，水下拖體作為一種高效且安全的平臺廣泛用于多種場合，如：水下勘探、海洋監測和水聲對抗等，平臺上可搭載多種聲吶探測設備、溫鹽深(CTD)傳感器和化學元素探測傳感器[1]，以完成各類科考或軍事任務。水下拖體屬于一類水下航行器，其外殼上一點與拖纜一端相連，拖纜另一端與拖曳母船連接。拖體的姿態控制一直是科研人員十分重視的課題，而其中俯仰控制又是姿態控制中非常重要的一環。由于拖體平臺的工作環境惡劣，工作要求苛刻，對于拖體的可控性需求也極其迫切。

國內外學者相繼開展了關于水下拖曳系統水動力理論和穩定性分析的研究[2-9]。Blintsov等[10]針對拖體在小深度拖曳情況下的特點，提出在不確定條件下使用局部功能最小化的方法進行運動控制，改進條件積分方法以消除工作中的積分飽和，基于2階控制律合成俯仰和橫滾控制器，并綜合單元旋轉運動控制系統以達到解耦的作用。Nakamura等[11]和Kajiware等[12]研究了具有自推進模式和拖曳模式的水下航行器 “DELTA”，在兩種模式下均設計了基于線性二次型積分(LQI)的控制器和基于線性矩陣不等式(LMI)的H∞魯棒控制器。之后考慮受到波浪振蕩和速度變化干擾的拖體，基于線性變參數(LPV)控制理論提出一種魯棒控制策略，該控制策略相較于PI控制和LQI控制有更好的效果。Campa等[13]認為可以使用H∞魯棒理論克服復雜非線性模型固有的不確定性，非線性和線性模型之間的差異以及其他未知干擾，提出了一種在設計過程中自動選擇加權函數的方法以及一種多變量識別過程的自適應方案，以在更廣的修整范圍內提高性能，Teixeira等[14]設計并證明了一種基于Lyaounov的非線性自適應控制器，以解決拖體的俯仰和深度控制問題。

考慮到一些水下航行器為了減輕質量、降低成本以及避免過多傳感器帶來的測量誤差和測量噪聲等目的，本身不會搭載足夠的傳感器，導致系統狀態變量無法全部反饋。針對這一問題，許多文獻提出設計觀測器的方法[15-21]，張利軍等[15-16]在文獻[15]中根據可測量的深度和縱搖角設計觀測器實現不可測縱搖角速度反饋，在文獻[16]中考慮近水面自主水下機器人(AUV)受波浪干擾，設計觀測器估計AUV姿態、速度和波浪位移、速度，并將系統輸出信號中的波浪干擾分離。Liu等[17-18]提出了一種用于AUV的非線性無源觀測器，無需聲學多普勒測速儀便可實現濾波操作以及對無法測量的波浪速度和AUV相對波浪速度的重建。楊盼盼等[19]設計了一種分布式觀測器，對AUV集群中鄰居速度信息進行實時估計。Minowa等[20-21]對一種拖體系統設計了高增益觀測器與線性卡爾曼觀測器進行狀態估計，并將估計值輸入基于LQI設計的魯棒控制器，用來控制拖體的深度和俯仰姿態。此外，水下航行器一般使用慣性測量單元(IMU)測量角速度，IMU需要安裝在航行器重心位置才可以比較準確地測量角速度。

本文研究對象拖體在執行不同種類任務時會搭載不同設備，有時甚至會外掛設備，拖體重心難免會發生變化，這種情況下IMU的測量精度無法保證，所以本文設計了一種基于神經網絡觀測器的拖體姿態補償控制系統，該系統由兩部分組成：一是狀態觀測器，二是補償滑模控制器，兩部分中各包含一個徑向基函數(RBF)神經網絡和獨立的權值更新自適應律，其中控制器部分含有一種映射修正自適應律，以保證控制律不會產生奇異，兩個RBF神經網絡在線辨識模型中的未知非線性函數。基于Lyapunov理論證明了系統的穩定性，仿真和實驗結果表明，所設計的補償控制系統可以保證當拖體存在有界干擾以及未建模動態情況時仍然具有良好的控制性能。

1 模型描述

通過對AUV六自由度動力學模型[22]修改并解耦后可得拖體垂直面俯仰通道動力學模型為

(1)

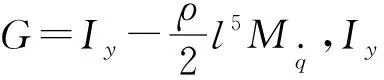
由(1)式可知拖體動力學模型具有較強的非線性和不確定性，考慮模型誤差和其他干擾，可表示為如下單輸入單輸出非線性系統：

(2)

2 基于觀測器的姿態補償控制系統

2.1 傳統狀態觀測器設計

對于系統(2)式，可以設計傳統狀態觀測器[23]如下：

(3)

(4)

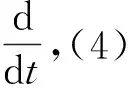
(5)

引理1如果AH是Hurwitz矩陣，Q是正定矩陣，而且嚴格正常有理函數H(s)=cT(sI-AH)-1b是嚴格正實的，I為單位矩陣，則一定存在正定矩陣P，滿足

(6)

引理2存在線性時不變狀態方程

(7)

式中：x(t)∈R，u(t)∈R，AH∈R，BH∈R. 初始值為x(0)=x0. 對(7)式中的任意解存在不等式

(8)

式中：k1隨x0以指數形式衰減為0的正常數；k2為與AH的特征值有關的正常數；α為正常數。

2.2 自適應神經網絡狀態觀測器設計

2.2.1 RBF神經網絡

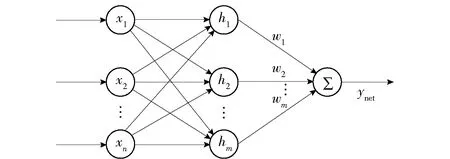
圖1 RBF神經網絡結構Fig.1 RBF neural network structure

考慮到觀測器(3)式中需要估計未知非線性函數f(x)和g(x)，可以采用RBF神經網絡[25-26]對其進行逼近估計，其結構如圖1所示。圖1中:x1、x2、…、xn為神經網絡輸入；w1、w2、…、wm為輸出層權值；m為輸出節點的數量；h1、h2、…、hm為隱含層輸出的非線性激活函數，ynet為網絡輸出。

(9)

式中：cj(t)為第j個隱含層神經元的中心點向量值；bj為隱含層神經元j的高斯基函數寬度，其值為正。網絡輸出為

(10)

式中：wi為輸出層權值。

2.2.2 觀測器誤差動態和結構

根據RBF神經網絡的函數逼近特性，系統(2)式中的未知非線性函數可以由理想權值W和基函數h表示為

(11)

(12)

因此，傳統觀測器(3)式和觀測誤差動態方程(4)式可寫為

(13)

和

(14)

為表述方便，后文中函數的部分自變量均省略。

(12)式代入(5)式，可得系統輸出估計誤差為

(15)

2.2.3 觀測器穩定性分析

對(15)式進行濾波處理：

(16)

(16)式的狀態空間實現為

(17)

假設控制輸入信號u(t)有界，即|u(t)|≤ud，針對觀測器方程(13)式，設計魯棒項為

(18)

定理1設計RBF神經網絡權值自適應律為

(19)

證明定義Lyapunov函數為

(20)

(21)

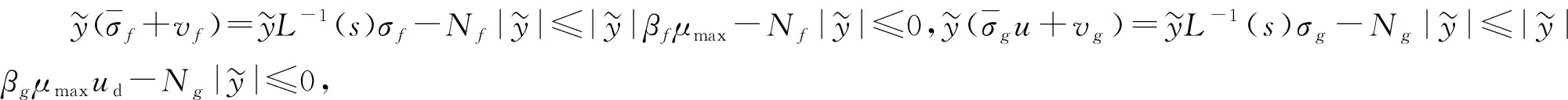
(22)

(23)

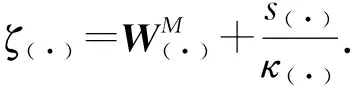
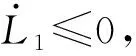
條件1

(24)

條件2

(25)

證畢。

(26)

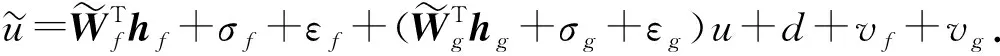
根據1階線性齊次微分方程求解公式，對(14)式求解，得

(27)

根據引理2和(26)式，可得

(28)

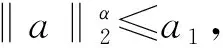
(29)

式中：a1、a2和a3為正常數。

2.3 自適應神經網絡補償滑模控制器

2.3.1 控制器結構和誤差動態方程

對于系統(2)式，考慮到系統狀態變量x由2.2節神經網絡狀態觀測器估計得到，記為，干擾d(t)視為未知非線性函數的一部分，即令f′()=f()+d(t)，則(2)式可寫為

(30)

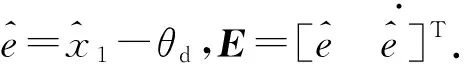
(31)

設計神經網絡權值自適應律為

(32)

設計滑模函數為

(33)

式中：c>0且滿足Hurwitz條件；設計滑模控制律為

(34)

式中：ψ>0.

(35)

式中：δ1和δ2為正常數；Pc是一個正定矩陣，且滿足

ΔTPc+PcΔ=-Qc，

(36)

Qc為任意正定2×2階矩陣。

基于觀測器的拖體俯仰姿態補償控制系統結構如圖2所示。

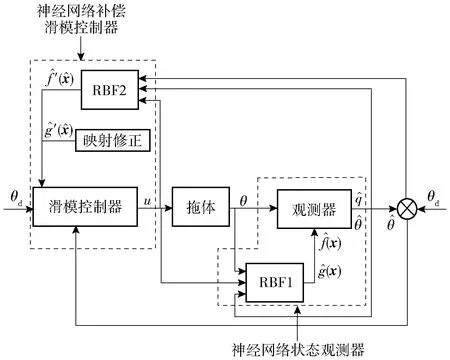
圖2 基于觀測器的拖體俯仰姿態補償控制系統結構圖Fig.2 Block diagram of observer-based attitude compensation control system for towed underwater vehicle

2.3.2 控制系統穩定性分析

控制律(34)式代入系統(30)式，得系統閉環動態方程的向量形式為

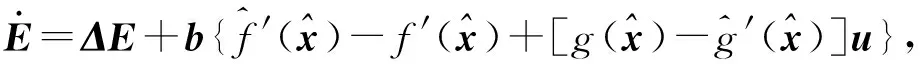
(37)

ω1=′(|W1)-f′())，

(38)

根據(31)式，(36)式可改寫為

(39)

定義Lyapunov函數為

L=L1+L2+L3，

(40)

式中：L2和L3分別為

(41)

(42)

(43)

神經網絡權值自適應律(32)式和映射修正自適應律(35)式代入(43)式，得

(44)

對L3求導并將滑模函數(33)式和動態方程(36)式代入，得

(45)

滑模控制律(34)式代入(45)式，則

(46)

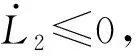
對映射修正自適應律進行分析，可得如下結論：

3 仿真算例與實驗結果

3.1 仿真算例

首先，在標稱情況下，設俯仰角指令為θd=0.1sin(t)，對補償控制系統和PD控制系統進行仿真計算，比較兩種控制系統的響應情況以及角速度的觀測精度。然后，在相同指令下，考慮存在水動力和力矩偏差、舵機死區、外界干擾以及拖纜張力變化的情況，比較兩種控制系統的魯棒性。

3.1.1 有效性檢驗

標稱情況下， 圖3(a)為兩種控制系統的正弦響應曲線，圖3(b)～圖3(d)為角速度的觀測結果和精度，圖3(e)為艉水平舵角響應曲線。由圖3可知：補償控制系統的響應曲線光滑，經過短時間的學習可以快速跟蹤俯仰角指令曲線；PD控制系統的響應曲線比較粗糙，尤其在曲線峰值處會出現小振蕩，跟蹤誤差較大；神經網絡觀測器能夠在角速度初始狀態存在偏差的情況下，僅用時1 s快速收斂到真實值，并隨后完成無差估計；傳統狀態觀測器始終存在較大的估計誤差。以上結果表明，在滿足一定條件下，本文所設計的3種自適應更新律和兩個RBF神經網絡可以對模型中的非線性、不確定部分進行在線辨識和實時補償，有效提高控制效果和觀測精度。

圖3 標稱情況下仿真結果Fig.3 Simulated results under normal conditions

3.1.2 魯棒性檢驗

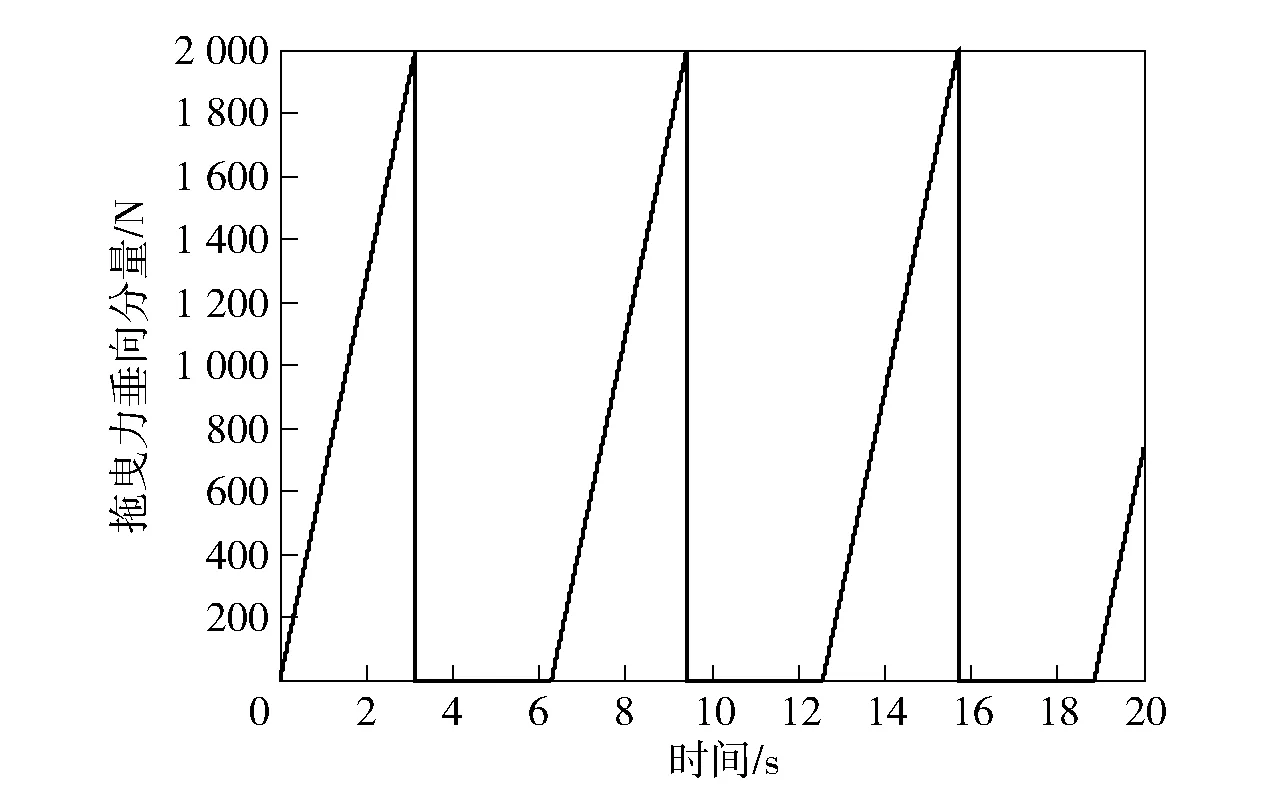
圖4 拖曳力垂向分量Fig.4 Vertical component of drag force

圖5 擾動情況下仿真結果Fig.5 Simulated results under disturbance conditions

3.2 實驗結果

以某型號拖體為實驗平臺，在海況約3級、拖體定深7～9 m、航速4～6 kn的工況下，得到控制算法實驗結果如圖6所示。由圖6可見，PD控制系統作用下的俯仰角變化范圍為-3°～8°，補償控制系統在經歷約20 s的學習過程后控制俯仰角穩定在0°～3°. 相比之下，補償控制系統的控制效果更出色。

4 結論

本文針對拖體俯仰姿態控制系統設計中模型強烈的非線性不確定性以及外部干擾的問題，提出了自適應神經網絡和映射修正自適應律逼近模型未知非線性部分和常數項的方法，實現了無需拖體精確模型的狀態觀測和補償控制。設計了兩種神經網絡權值更新自適應律，實現兩種神經網絡在線辨識拖體非線性動力學模型并加入魯棒項抑制附加干擾，以及一種映射修正自適應律，保證控制律不產生奇異。基于Lyapunov理論證明在滿足一定條件時系統的誤差是最終一致有界的。仿真和實驗結果表明，本文設計的補償控制系統具有優異的魯棒性和自適應性，可以在模型系統存在水動力和力矩偏差、舵機死區、外部干擾以及拖曳力變化的情況下，實現對系統狀態的精確估計和有效控制。