基于超混沌與分塊操作的快速圖像加密算法

楊 丹，謝淑翠，張建中

(1.西安郵電大學 通信與信息工程學院，陜西 西安 710119；2.西安郵電大學 理學院，陜西 西安 710119；3.陜西師范大學 數學與信息科學學院，陜西 西安 710119)

0 引 言

近年來，研究人員一直在努力尋找圖像加密[1]的最優方法，由于混沌具有初值敏感性，非周期性和不可預測性[2]，許多學者利用混沌系統產生密鑰流從而加密圖像。這種方法通常有兩個步驟組成：像素置亂和擴散，在置亂過程中，像素的位置被改變，在擴散過程中，像素的值被改變[3]。

目前，研究者提出了許多基于混沌的圖像加密算法，其中一些算法不是被發現不安全就是時間開銷過大。文獻[4,5]均提出了超混沌圖像的加密算法，魯棒性好安全性高，但加密速度不夠理想；文獻[6]提出了新型置換和替代加密算法，增加破解難度，但采用一維混沌系統，密鑰空間小安全性不高；文獻[7]提出了一種典型的圖像加密算法，具有結構簡單加密速度快的優點，卻存在安全問題，主要是因為其等效密鑰與明文無關，無法抵抗選擇明文攻擊。如果一種加密算法具有較高的安全級別，但運行很耗時，就不適合于實時加密環境。因此，需要設計具有高安全性的快速圖像加密方案，以滿足實時通信的要求。基于以上分析，本文提出一種基于超混沌和分塊操作的快速圖像加密算法。算法的圖像置亂過程是以塊為單位，包括塊間交換及塊內循環，以期提高加密效率，節省時間。通過建立密鑰和明文的關聯，提高密鑰敏感性。利用動態密鑰進行擴散，增強安全性。我們對圖像灰度分布、相鄰像素相關性、密鑰空間、密鑰敏感性、加密速度、抗差分攻擊能力及抗噪聲和裁剪的魯棒性進行了深入分析和仿真實驗，結果表明本算法具有較高的安全性及較快的運行速率。

1 動態原始序列的產生

本文采用超混沌Lorenz系統[8]產生混沌序列

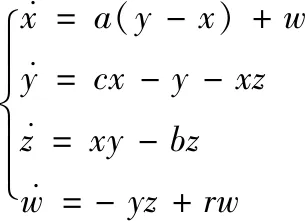
(1)

其中，a,b,c,r為系統控制參數，x,y,z,w為系統的狀態變量。當a=10,b=8/3,c=28, -1.52≤r≤-0.06時，系統(1)表現為混沌運動。取r=-1，用matlab R2016a進行仿真，得到的吸引子相圖如圖1所示，可見系統(1)具有極其復雜的動力學特性，運動軌跡難以預測，適合用于圖像加密。

假設明文圖像為P，大小為M×N。 為了消除暫態過程帶來的影響，系統(1)用龍格庫塔算法迭代N0(N0≥1000) 次，接著選擇與明文相關的動態原始序列

I=mod(p(n),4)

(2)

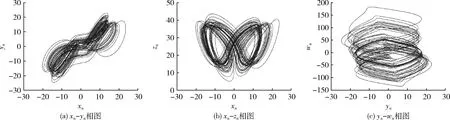
圖1 系統(1)的部分吸引子相圖

當I=0,I=1,I=2,I=3，分別從x,y,z,w中進行取樣，用取樣的值組成原始動態序列D，大小為M×N。

2 加密算法

加密算法包括兩個步驟：像素置亂和擴散。

2.1 像素置亂

將P分成m1·n1個小塊，其中m1能整除M，n1能整除N，經過塊間交換和塊內循環得到置亂圖像Q。

2.1.1 塊間交換

沿著不同方向進行兩輪的塊交換，每個塊和另一個塊進行交換，塊間交換的位置由K1控制，K1由下式產生

temp=floor((abs(D)-floor(abs(D)))×10^14)
K1=mod(temp,256)

(3)

其中，abs(x) 為x的絕對值，floor(x) 為小于等于x的最大整數，K1∈[0,255]。

假設一個塊圖像的位置為 (p1,q1)，和它交換的另一個塊圖像的位置為 (p2,q2)，(p2,q2) 由下式確定

(4)

(5)

其中，temp1=1,2…,m1，temp2=m1+1,…,m1+n1，g1=inverse(temp1),g2=inverse(temp2)，inverse表示逆序數。塊與塊之間的交換由式(6)表示

P′p1,q1=Pp2,q2；P′p2,q2=Pp1,q1

(6)

其中，P′p1,q1表示在 (p1,q1) 位置處交換后的塊圖像，Pp2,q2表示在 (p2,q2) 處的塊圖像。

第一輪塊置換是從第一行掃描到第m1行，第二輪塊置換是從第一列掃描到第n1列，經過兩輪塊置亂后的圖像記為A。

2.1.2 塊內循環

將A按塊排成一列，每個子塊是m×n的矩陣，總共m1×n1個子塊，每個子塊內的像素用索引矩陣Hm和Hn中的不同元素進行兩個方向的循環移位，即Hm和Hn中的元素分別表示向右、向下循環移位的位數。步驟如下：

步驟1 由式(7)產生大小為M×N的S1序列

S1=mod((floor(D×10^14)),256)

(7)

步驟2 從S1中選m=M/m1個數作為Hm的第一行，再選m個數作為Hm的第二行，選取m1·n1次，直到Hm成為m1·n1行，m列的矩陣。同理從S1選數使Hn成為m1·n1行，n=N/n1列的矩陣；

步驟3 進行循環右移，第一個子塊中的m行由Hm中第一行的m個數控制進行循環右移，第二個子塊中的m行由Hm中第二行的m個數控制進行循環右移，以此類推，直到循環右移完所有的子塊；

步驟4 接著進行循環下移，第一個子塊中的n列由Hn中第一行的n個數控制進行循環下移，第二個子塊中的n列由Hn中第二行的n個數控制進行循環下移，以此類推，直到循環下移完所有的子塊。

2.2 像素擴散

為了進一步提高加密算法的安全性，還需進行像素擴散，擴散使用的密鑰為K2

K2=mod(fix(D×10^3),256)

(8)

fix(x) 為向0取整。將置亂圖Q轉化成一維序列進行如下操作

(9)

這里，T為預先設定的參數。

3 解密算法

圖像解密是加密的相反操作，其中擴散的解密執行下式

(10)

接著進行置亂的解密操作，首先將經過上式解擴散得到的圖分成m1·n1的子塊，每個子塊中的像素進行循環上移和循環左移，接著進行兩輪塊間交換的解密操作：第一輪按列掃描，第二輪按行掃描，最終得到解密圖。

4 仿真結果和安全性分析

本文采用512×512的Lena圖，在Win7操作系統下，以MATLAB R2016a為平臺進行仿真。超混沌Lorenz系統的初始密鑰設為x0=1.1,y0=2.2,z0=3.3,w0=4.4,r=-1。 加密過程中的參數設為T=1。 對Lena進行加解密如圖2所示，可見加密圖像隱藏了明文信息，確保了傳輸安全，并且解密圖像可以很好地恢復出明文圖像。下面給出詳細分析。

圖2 加密和解密

4.1 信息熵

信息熵反映圖像信息的不確定性，通常被認為熵越大，不確定性越大，可視信息越少[9]。對于灰度等級為L的圖像，假設灰度值i出現的概率為p(i)，信息熵計算公式如下

(11)

對于L=256的灰度隨機圖，信息熵的理論值為8[10]。經過本算法加密的密文圖像的信息熵為7.9992，接近理想值，表明本文算法可以生成隨機性更好的密文圖像。

4.2 直方圖分析

直方圖是用來顯示像素分布特性的，在加密算法中，改變分布特性是十分重要的。圖3(a)和圖3(b)分別表示明文圖像和加密圖像的直方圖，可以看出原始明文圖像具有明顯的統計特性，而加密圖像每個灰度值出現的概率趨于相等，因此對密文圖像進行基于頻率的攻擊是無效的[11]。

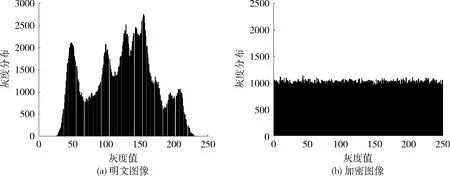
圖3 加密前后的直方圖

4.3 相關性分析

圖像中相鄰像素之間通常具有很強的相關性，因此一個好的加密算法應該能夠產生具有低相關性的密文圖像，從而隱藏圖像信息，抵抗統計攻擊[12]。相鄰像素相關性由下式確定

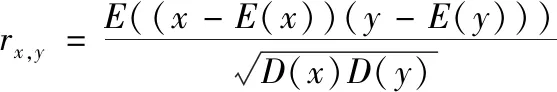
(12)

其中，E(x) 和D(x) 分別為變量x的期望和方差，rx,y為相鄰像素x和y的相關系數。

從Lena測試圖和它的加密圖中隨機選取3000對相鄰像素進行相關性分析，測得水平方向的相關分布如圖4所示，可以看出，明文圖像的相鄰像素值位于斜率為1的直線附近，這表明相鄰兩個像素的相關性較高；密文圖像的像素值布滿整個區域，這表明相鄰兩個像素的相關性較低。表1給出了本文在水平、垂直、對角3個方向相關性的測試值，可以看出，明文圖像的相鄰像素具有較高相關性 (rxy→1)，密文圖像的相鄰像素具有較低相關性 (rxy→0)，同時與文獻[13]和文獻[14]的相應結果進行對比，表明本文所提出的加密算法相鄰像素的相關性更低，可以更有效抵抗統計攻擊[15]。

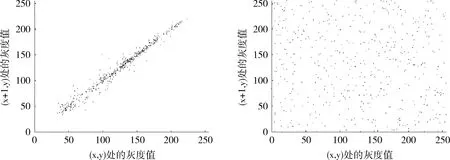
圖4 相鄰像素水平方向的相關分布

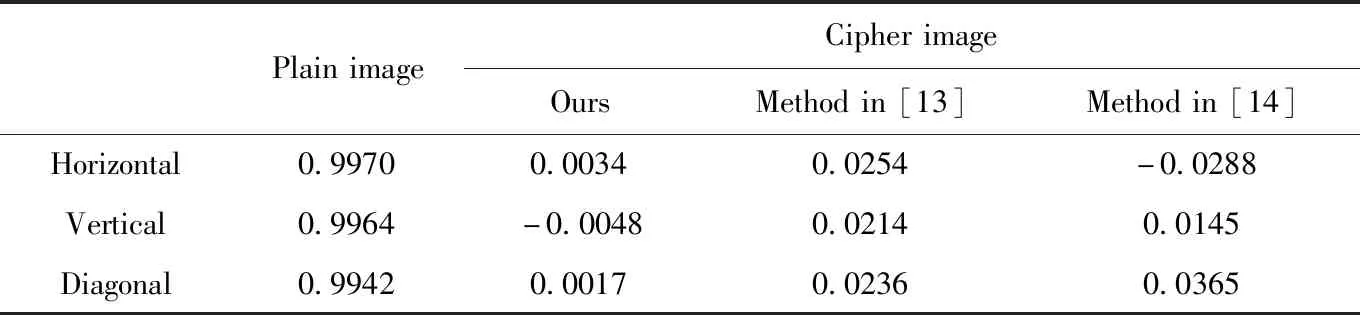
表1 相鄰像素的相關系數

4.4 敏感性分析

加密算法對密鑰和明文敏感意味著微小改變密鑰和明文將會產生完全不同的加密結果。通常有兩個指標衡量：像素變化率(number of pixels change rate，NPCR)和歸一化像素平均改變強度(unified average changing intensity，UACI[16])。NPCR的計算公式為

(13)

UACI的計算公式為

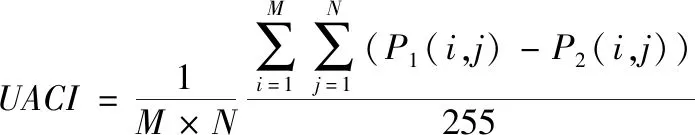
(14)

其中，P1和P2為兩幅大小為M×N的圖像。

為了衡量密鑰敏感性，取密鑰x0=1.1,y0=2.2,z0=3.3,w0=4.4加密原始明文圖5(a)并得到加密圖5(b)，輕微改變z0(z0+10-12) 后再次對圖5(a)進行加密得到圖5(c)，圖5(d)為圖5(b)和圖5(c)的差分圖。圖5(e)和圖5(f)分別是用正確密鑰解密圖5(b)和用微小改變的密鑰解密圖5(b)的解密圖。圖5(a)和圖5(b)間的NPCR和UACI分別為99.60%,33.45%，它們均接近相應的理想值NPCR=99.6094%,UACI=33.4635%[8]，這表明本文算法具有強的密鑰敏感性。

圖5 密鑰敏感性

為了衡量明文敏感性，用上述相同的密鑰加密圖5(a)并得到加密圖6(a)，輕微改變明文圖像(第4個像素最低位取反)并且加密該明文圖像得到相應的加密圖6(b)，圖6(c)為圖6(a)和圖6(b)的差分圖。圖6(a)和圖6(b)間的NPCR和UACI分別為99.62%,33.46%，它們均接近相應的理想值NPCR=99.6094%,UACI=33.4635%[8]，這表明本文算法具有強的明文敏感性。

4.5 密鑰空間分析

本文算法密鑰由4個初值 (x0,y0,z0,w0) 和控制參數r組成，采用精確到小數點后15位的浮點數表示，密鑰空間可達到1015×1015×1015×1015×1015=1075≈2249，文獻[17]的密鑰空間為1073，且本文加密過程中的初值T也可作為密鑰。由此可見，本文算法有更大的密鑰空間，能更好地抵抗窮舉攻擊。

圖6 明文敏感性

4.6 加密速度

在實時系統中，除了對安全性有高的要求外，加密時間還需盡可能的短，以達到較高的實用性。表2是本文與文獻[18]加密速度的比較，結果表明，本文在加密速度方面尤其對較大圖像具有較強的優勢。

表2 加密速度對比/s

4.7 抗差分攻擊

差分攻擊是一種選擇明文攻擊，抗差分攻擊性能依賴于對明文的敏感性，通常用NPCR和UACI來衡量。我們分別對兩幅圖像進行加密，一幅為原始明文圖像，另一幅為明文圖像隨機選擇一個像素點并將該像素的最低位取反，計算得NPCR=99.50%，UACI=33.43%。 它們均接近其灰度圖像的對應理想值：NPCR=99.6094%，UACI=33.4635%[7]，所以該算法具有強的抗差分攻擊能力。

4.8 抗噪聲及抗裁剪攻擊的魯棒性分析

在傳輸過程中，密文圖像會受到種種的干擾及攻擊，一個好的加密算法還需使圖像對外界的干擾具有魯棒性[19]。

抗噪聲攻擊分兩種情況進行分析。第一種，圖像加密前被噪聲污染，在原始明文圖像中加入均值為0，方差為0.05的椒鹽噪聲如圖7(a)所示，經過加密得到密文圖像如圖7(b)所示，到接收端進行解密后使用中值濾波器進行濾波得到圖7(c)。由圖可見，即使明文圖像受到噪聲污染后，原始圖像也可以通過加密、解密、濾波來恢復。第2種是在傳輸過程中密文圖像被噪聲污染，圖8(a)和圖8(b)分別為密文圖像和受均值為0，方差為0.0005高斯噪聲污染的密文圖像，在接收端進行解密得到圖8(c)，可以看出，解密后的圖像仍有噪聲，但能恢復出原始圖像的主要信息，可以根據實際需要進一步進行去噪處理。由以上分析可知，本文加密算法在微噪聲的污染下仍能恢復有效的信息，對噪聲具有較強魯棒性。

圖7 椒鹽噪聲污染測試

圖8 高斯噪聲污染測試

在抗裁剪攻擊的分析中，我們分別對密文圖像進行不同位置、不同大小的裁剪，然后對裁剪后的圖像進行解密，如圖9所示。由圖可見，在對密文經過各種裁剪后，解密后的明文圖像仍具有較高的辨析度，這表明本文算法對裁剪攻擊具有很好的魯棒性。

圖9 裁剪攻擊測試

5 結束語

本文提出了一種基于超混沌與分塊操作的快速圖像加密算法，首先通過超混沌Lorenz系統構建動態原始序列D，該序列用來產生置亂和擴散的密鑰，其次對圖像進行分塊處理，實行塊間置亂及塊內移位從而實現像素置亂，使加密速度得到較大提升，接著利用動態密鑰進行像素擴散以實現圖像加密。理論分析和仿真結果表明，本文所提出的算法具有更大的密鑰空間，更高的密鑰敏感性以及更快的運行速度，能有效抵抗統計攻擊和差分攻擊等攻擊手段，對噪聲及裁剪具有較好的魯棒性。因此，本文所提出的算法在實時保密通信中具有較大的應用價值。