拉索失效對(duì)多重四邊環(huán)索-張弦穹頂?shù)挠绊?/h1>
2020-02-16 14:48:14張超付馨迪許莉顏學(xué)淵賈宏宇
湖南大學(xué)學(xué)報(bào)·自然科學(xué)版 2020年1期
張超 付馨迪 許莉 顏學(xué)淵 賈宏宇
摘???要:多重四邊環(huán)索-張弦穹頂結(jié)構(gòu)作為一種新型的索支穹頂結(jié)構(gòu),拉索失效會(huì)對(duì)屋蓋結(jié)構(gòu)受力產(chǎn)生較大影響.?以全國(guó)首座三重四邊環(huán)索-張弦穹頂屋蓋(福州海峽奧林匹克中心體育館屋蓋)為研究背景,研究了拉索失效對(duì)于此類新型索支穹頂結(jié)構(gòu)的豎向剛度、構(gòu)件內(nèi)力及極限承載能力的影響規(guī)律,并評(píng)估單根拉索失效后屋蓋結(jié)構(gòu)的安全性.?分析結(jié)果表1明:拉索失效均會(huì)引起屋蓋顯著下?lián)希鞣N工況中外環(huán)索失效會(huì)引起最大的屋蓋下?lián)希牵煌魇Ш笪萆w豎向變形分布規(guī)律相差較大;外環(huán)索和張弦索的失效會(huì)引起相鄰拉索索力不同程度的增大;外環(huán)索與張弦索的相互影響大于各環(huán)索之間的相互影響;不同位置的拉索失效均會(huì)引起屋蓋極限承載能力下降,外環(huán)索失效引起結(jié)構(gòu)極限承載力下降最顯著;“僅單側(cè)張弦索失效”會(huì)引起較“兩側(cè)張弦索均失效”更不利的屋蓋撓度和極限承載力.?總之,外環(huán)索失效為最不利拉索失效工況,會(huì)引起屋蓋最大撓度增大134%,張弦索索力增加11.7%,極限承載力減小35%.?但是,剩余整體屋蓋結(jié)構(gòu)仍具有一定的安全性.
關(guān)鍵詞:多重環(huán)索;張弦梁;穹頂;拉索失效;極限承載能力
中圖分類號(hào):TU356???????????????????????文獻(xiàn)標(biāo)志碼:A
Influence?of?Multiple?Square?Loops-string?Dome?Subjected?to?Cable?Failure
ZHANG?Chao1,2,F(xiàn)U?Xindi1,XU?Li1,YAN?Xueyuan1?,JIA?Hongyu3
(1.?College?of?Civil?Engineering,F(xiàn)uzhou?University,F(xiàn)uzhou?350108,China;
2.?Key?Laboratory?of?Urban?Security?&?Disaster?Engineering?(Beijing?University?of?Technology)?of?the?MOE,Beijing?100124,China;
3.?School?of?Civil?Engineering,Southwest?Jiaotong?University,Chengdu?610031,China)
Abstract:Multiple?square?loops-string?dome?is?a?newly?suspen-dome?structure,and?cable?failure?shows?significant?effect?on?multiple?square?loops-string?dome?structures.?This?paper?used?the?Fuzhou?Strait?Olympic?Center?Gymnasium?as?the?research?background?to?study?the?effect?of?cable?on?the?vertical?stiffness?of?the?roof,the?internal?forces?of?the?roof?and?the?ultimate?bearing?capacity,and?safety?capability?evaluation?of?the?cable?failure?roof?was?carried?out.?The?analysis?results?show?that?the?vertical?deformation?of?the?roof?can?be?reduced?after?cable?failure.?Among?them,the?failure?of?the?outer?loop?cable?causes?the?maximum?vertical?deformation.?However,various?vertical?deformation?distributions?subjected?to?different?cable?failure?are?generated.?The?failure?of?either?the?outer?loop?or?string?cable?can?increase?the?tension?force?of?the?adjacent?cable?significantly.?The?interaction?between?the?outer?loop?cable?and?string?cable?is?greater?than?the?mutual?influence?between?the?other?loop?cables;?Ultimate?bearing?capacity?of?the?roof?can?be?reduced?when?cable?failure?occurs,which?reaches?the?minimum?value?when?the?outer?loop?cable?fails.?It?should?be?noted?that?“Only?one?side?string?cable?failure”?causes?more?serious?deflection?and?less?ultimate?bearing?capacity?when?compared?with“two?side?string?cable?failure”.?In?all,failure?of?the?outer?loop?cable?is?the?most?serious?case,which?causes?that?vertical?deflection?increases?by?134%,the?cable?tension?force?of?adjacent?cable?increases?by?11.7%,and?the?ultimate?bearing?capacity?reduces?by?35%.?However,the?residual?roof?structure?is?still?in?a?safe?state.
Key?words:multiple?square?loops;beam?string;domes;cable?failure;ultimate?bearing?capacity
弦支穹頂結(jié)構(gòu)是由日本政法大學(xué)川口衛(wèi)教授于1993年提出的一種新型雜交空間結(jié)構(gòu)[1],具有造型美觀、節(jié)省材料、質(zhì)量輕、剛度大、抗震性能好等空間結(jié)構(gòu)的綜合優(yōu)勢(shì),在大型的公共與工業(yè)建筑中得到廣泛應(yīng)用.?典型的工程應(yīng)用包括日本前橋綠色會(huì)館、日本北九州穴生屋頂、濟(jì)南奧體中心體育館、常州體育館、2008年北京奧運(yùn)會(huì)羽毛球館等.
1963年1月,羅馬尼亞布加勒斯特市一座直徑為93?m的國(guó)家經(jīng)濟(jì)展覽館穹頂網(wǎng)殼在近1?m厚積雪作用下失穩(wěn)倒塌.?此后,網(wǎng)殼結(jié)構(gòu)的安全問題成為人們研究的熱點(diǎn).?索結(jié)構(gòu)屬于柔性結(jié)構(gòu)體系,預(yù)應(yīng)力的引入可顯著改善網(wǎng)格結(jié)構(gòu)的整體變形、桿件內(nèi)力峰值和整體穩(wěn)定承載力[2].雖然在索穹頂結(jié)構(gòu)設(shè)計(jì)中,拉索的設(shè)計(jì)應(yīng)力只取索強(qiáng)度的30%~50%,且均采用強(qiáng)度較高的鋼材,不容易發(fā)生破斷,但實(shí)際使用過程中依然會(huì)因材料質(zhì)量缺陷、維護(hù)缺陷、加工和施工缺陷等偶然因素引起某根索的破斷,造成結(jié)構(gòu)整體性垮塌.
對(duì)于預(yù)應(yīng)力索桿結(jié)構(gòu)的斷索安全性,國(guó)內(nèi)外學(xué)者已開展了相關(guān)研究,如索穹頂[3]、張拉整體[4]、張弦桁架[5]、弦支穹頂[6-9]、索桿結(jié)構(gòu)[10-13]等.?朱明亮等[7]對(duì)一種由周邊環(huán)形張拉整體和中部索穹頂組成的新型環(huán)箍-穹頂全張力結(jié)構(gòu)進(jìn)行靜力和動(dòng)力分析,發(fā)現(xiàn)張拉整體單元的拉索破斷主要影響所在單元附近拉索,不會(huì)形成連續(xù)倒塌.?姜正榮等[12]對(duì)Levy型索穹頂結(jié)構(gòu)索桿破斷進(jìn)行敏感性分析,發(fā)現(xiàn)Levy型索穹頂對(duì)環(huán)索和中心撐桿的破斷最為敏感,其中最外環(huán)圈環(huán)索破斷對(duì)應(yīng)的敏感性系數(shù)最大.?高占遠(yuǎn)等[13]運(yùn)用瞬態(tài)動(dòng)力學(xué)的Newmark時(shí)間積分法對(duì)單根索桿斷裂后結(jié)構(gòu)的力學(xué)性能進(jìn)行分析,并提出一種桿件重要系數(shù),發(fā)現(xiàn)外環(huán)桿的重要性排在首位,內(nèi)脊索排在末位.?然而,目前對(duì)于拉索失效影響的分析僅是針對(duì)傳統(tǒng)弦支穹頂結(jié)構(gòu),由多重四邊環(huán)索、張弦索組合形成的復(fù)雜弦支穹頂屋蓋,各重拉索體系的受力相互影響,某局部拉索失效后,剩余拉索體系(同一環(huán)索中剩余拉索及其他重環(huán)索)會(huì)進(jìn)行復(fù)雜的內(nèi)力重分布,對(duì)于屋蓋結(jié)構(gòu)的影響規(guī)律可能會(huì)顯著區(qū)別于傳統(tǒng)索穹頂結(jié)構(gòu).?因此,本文以全國(guó)首個(gè)三重四邊環(huán)索-張弦索組合穹頂屋蓋——福州海峽奧林匹克中心體育館工程為研究背景,研究可能發(fā)生的拉索失效對(duì)于此類新型索支穹頂屋蓋結(jié)構(gòu)的剛度、內(nèi)力、穩(wěn)定極限承載能力的影響規(guī)律,并評(píng)估單根拉索斷裂后屋蓋結(jié)構(gòu)的安全性.
1???工程背景及數(shù)值模型
1.1???工程背景
福州海峽奧林匹克中心體育館屋蓋采用多重四邊環(huán)索-張弦穹頂結(jié)構(gòu),由網(wǎng)格梁、撐桿、斜索、四邊形環(huán)索、張弦梁構(gòu)成,其中各層撐桿與網(wǎng)格梁和索的連接均為鉸接.?屋蓋跨度約97?m?×?116?m,周圍混凝土柱作為屋蓋結(jié)構(gòu)的內(nèi)支座,弦支結(jié)構(gòu)網(wǎng)格梁與支座剛接,網(wǎng)格梁采用矩形截面鋼管.?為保證屋蓋結(jié)構(gòu)的空間幾何穩(wěn)定性,并避免壓桿側(cè)向失穩(wěn),本結(jié)構(gòu)在網(wǎng)格梁中設(shè)置十字交叉形和V形兩種形式的屋面支撐,采用圓形截面鋼管.?屋蓋網(wǎng)格梁、撐桿、支撐等型鋼構(gòu)件均采用Q345,混凝土柱采用C40.?此屋蓋結(jié)構(gòu)東西方向?qū)ΨQ,北側(cè)屋蓋標(biāo)高高于南側(cè),且北側(cè)網(wǎng)格梁橫向跨度略大于南側(cè)網(wǎng)格梁.
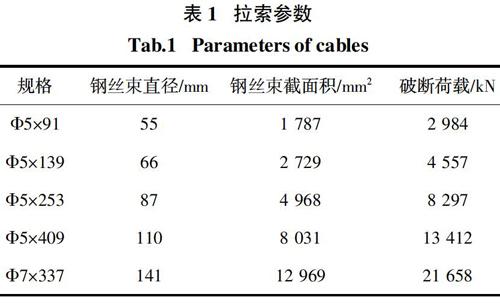
三重四邊環(huán)索成矩形,第一環(huán)(內(nèi)環(huán))撐桿高度9.0?m,四邊形環(huán)索長(zhǎng)21.6?m、19.0?m,斜索長(zhǎng)13.9?m、15.0?m;第二環(huán)(中環(huán))撐桿9.0?m,四邊形環(huán)索長(zhǎng)37.9?m、36.0?m,斜索長(zhǎng)13.4?m、14.85?m;第三環(huán)(外環(huán))撐桿9.5?m,四邊形環(huán)索長(zhǎng)56.9?m、51.1?m,斜索長(zhǎng)度15.8?m、18.2?m.?為增加豎向剛度,在四邊形環(huán)索第三環(huán)增設(shè)中間撐桿,高13.0?m,在東西兩側(cè)設(shè)置獨(dú)立張弦結(jié)構(gòu),撐桿高度8.5?m、11.0?m,索規(guī)格及相關(guān)參數(shù)見表11.
1.2???三維數(shù)值模型建立
本文采用SAP2000建立三維空間數(shù)值模型,如圖1所示.?其中,網(wǎng)格梁為箱型截面,屋面支撐為圓形截面鋼管,均采用Frame單元模擬,鋼材彈性模量為206?GPa;預(yù)應(yīng)力拉索采用Cable單元模擬,拉索彈性模量為195?GPa.?“型鋼混凝土環(huán)梁”和“混凝土柱”均采用Frame單元模擬,截面特性均按照實(shí)際截面計(jì)算;根據(jù)環(huán)梁與混凝土柱剛接的實(shí)際情況,數(shù)值模型中,混凝土柱頂節(jié)點(diǎn)與環(huán)梁節(jié)點(diǎn)剛接;混凝土柱底則為固端約束.
(c)屋蓋變形監(jiān)測(cè)節(jié)點(diǎn)
圖2???關(guān)鍵構(gòu)件編號(hào)示意圖
Fig.2???Numbering?diagram?of?key?components
1.3???基準(zhǔn)數(shù)值模型驗(yàn)證
為驗(yàn)證本文所建數(shù)值模型的準(zhǔn)確性,按實(shí)際屋蓋施工過程中拉索張拉情況,定義非線性階段施工工況,采用短鏈桿的溫降收縮[14]模擬索力張拉過程,得到不同索力張拉過程中各監(jiān)測(cè)關(guān)鍵點(diǎn)的受力及變形.?監(jiān)測(cè)關(guān)鍵點(diǎn)布置情況如圖3(a)、圖4(a)所示.
圖3(b)、圖4(b)分別表1示網(wǎng)格梁應(yīng)力和屋蓋節(jié)點(diǎn)撓度的實(shí)測(cè)數(shù)據(jù)與模型計(jì)算結(jié)果的對(duì)比.?從圖3(b)中可看出,實(shí)測(cè)數(shù)據(jù)與模型計(jì)算結(jié)果相差較小,誤差最大的為16號(hào),實(shí)測(cè)數(shù)據(jù)與模型計(jì)算值相差16.1?MPa.?從圖4(b)中可看出,實(shí)測(cè)數(shù)據(jù)的撓度值略小于模型計(jì)算值,但兩者相差較小,誤差最大的為6號(hào)節(jié)點(diǎn),二者相差10.1?mm.?由于篇幅有限,其監(jiān)測(cè)結(jié)果對(duì)比詳見文獻(xiàn)[15].
總之,各施工階段的數(shù)值模擬結(jié)果與實(shí)際施工監(jiān)測(cè)數(shù)據(jù)總體吻合較好,誤差均在可接受的范圍內(nèi).?因此,本文在后續(xù)分析中,以此數(shù)值模型為基準(zhǔn)分析模型.
2???完整屋蓋結(jié)構(gòu)的響應(yīng)規(guī)律
2.1???變形及內(nèi)力響應(yīng)
在上節(jié)基準(zhǔn)數(shù)值模型的基礎(chǔ)上,健康狀態(tài)下的完整屋蓋結(jié)構(gòu)(后文簡(jiǎn)稱“完整屋蓋”,以區(qū)分于拉索失效后屋蓋結(jié)構(gòu))在實(shí)際運(yùn)營(yíng)過程中,應(yīng)考慮屋面蓋板等二期附加恒載以及屋蓋活荷載的組合作用,其中,附加恒載為0.823?kN/m2,活載為0.5?kN/m2.?本文按“1.0附加恒載+1.0活載”考慮正常使用階段的荷載組合.
在正常使用階段荷載組合作用下,完整屋蓋的變形和軸向應(yīng)力如圖5、圖6所示,其中跨中節(jié)點(diǎn)位移最大,達(dá)106?mm,小于規(guī)范[16]規(guī)定屋蓋跨中撓度控制值388?mm?(L/250,L為完整屋蓋短跨).?外環(huán)斜索附近屋面支撐的壓應(yīng)力最大,約為127?MPa,但小于Q345鋼材的抗壓強(qiáng)度設(shè)計(jì)值f?(310?MPa).
豎向撐桿可看作是兩端鉸接的軸心受壓構(gòu)件.?本屋蓋體系中各類型撐桿軸壓力及截面應(yīng)力見表12.?根據(jù)《鋼結(jié)構(gòu)設(shè)計(jì)規(guī)范》[16]需要對(duì)受壓構(gòu)件進(jìn)行強(qiáng)度承載力和穩(wěn)定承載力驗(yàn)算.?根據(jù)穩(wěn)定承載力驗(yàn)算,截面應(yīng)力應(yīng)小于φf.?其中,f為鋼材的軸心受壓強(qiáng)度,設(shè)計(jì)值為310?MPa;φ為軸壓構(gòu)件穩(wěn)定系數(shù),根據(jù)構(gòu)件的長(zhǎng)細(xì)比、鋼材屈服強(qiáng)度和截面分類按規(guī)范[16]中附錄C采用.?穩(wěn)定性驗(yàn)算結(jié)果見表13,所有豎向撐桿的穩(wěn)定承載力滿足設(shè)計(jì)要求,并有一定的富余度.
表13、表14分別為各個(gè)位置的水平拉索及斜索索力分布.?可以看出:各重環(huán)的索力分布基本呈對(duì)稱狀
態(tài),南北向的索力均大于東西向的索力;同一重環(huán)的斜索索力大于環(huán)索索力;索力從內(nèi)環(huán)到外環(huán)依次增大,水平索中,H34索力最大,達(dá)到3?192?kN,小于其對(duì)應(yīng)的破斷荷載(13?412?kN);斜索中,X34索力最大,達(dá)到4?348?kN,遠(yuǎn)小于其對(duì)應(yīng)的破斷荷載(216?58?kN).
2.2???極限承載能力
一般認(rèn)為,弦支穹頂結(jié)構(gòu)中的單層網(wǎng)殼屬于缺陷敏感性結(jié)構(gòu),其臨界荷載可能會(huì)因極小的初始幾何缺陷而大大降低.?同時(shí),文獻(xiàn)[17]發(fā)現(xiàn)單層蜂窩型球面網(wǎng)殼因受到初始缺陷影響,其極限承載力不斷下降.?因此本文采用一致缺陷模態(tài)法[18]來考慮屋蓋的初始缺陷.?其中,初始缺陷按第一階整體線性屈曲模態(tài)分布方式(如圖7所示),表1現(xiàn)為:沿南北向屋蓋豎向?qū)ΨQ振動(dòng),沿東西向屋蓋豎向反對(duì)稱振動(dòng).?缺陷最大值按屋蓋短跨跨度(L)的1/300選取.
為探討完整屋蓋的極限承載力,本文在對(duì)完整屋蓋施加初始缺陷后,進(jìn)行考慮幾何、材料雙重非線性的彈塑性極限承載力分析.?在彈塑性數(shù)值模型中,網(wǎng)格梁兩端設(shè)置彎矩鉸,屋面支撐和豎向撐桿設(shè)置軸力鉸來模擬材料非線性.?其中,以1#網(wǎng)格梁為例(見圖2(c)),列出計(jì)算的彎矩鉸的彎矩-曲率曲線如圖8所示;計(jì)算得到的2#屋面支撐(見圖2(c))軸力鉸的力-位移曲線如圖9所示.?圖8和圖9中,點(diǎn)B代
圖10給出了完整屋蓋的極限承載力-位移曲線,為對(duì)比材料非線性的影響,對(duì)結(jié)構(gòu)在考慮初始缺陷基礎(chǔ)上進(jìn)行彈塑性分析的同時(shí),還進(jìn)行了僅考慮幾何非線性的彈性分析[19].?可看出:完整屋蓋的彈性極限承載力為66.7?MN,彈塑性極限承載力為56.1?MN.?說明彈性極限承載力會(huì)過高地估計(jì)屋蓋結(jié)構(gòu)承載力.?因此,后文計(jì)算屋蓋結(jié)構(gòu)極限承載力時(shí)均考慮屋蓋結(jié)構(gòu)的幾何、材料雙重非線性因素的影響.
3???拉索失效后屋蓋結(jié)構(gòu)的響應(yīng)規(guī)律
3.1???拉索失效分析工況研究
本文數(shù)值分析中,采用變換荷載路徑法[20]模擬拉索失效,即基于完整屋蓋結(jié)構(gòu)的數(shù)值模型,通過“移除”相應(yīng)的失效單元,得到拉索失效后的屋蓋結(jié)構(gòu),進(jìn)一步分析拉索失效后屋蓋結(jié)構(gòu)的變形響應(yīng)、內(nèi)力分布及極限承載力,進(jìn)而評(píng)估拉索失效后屋蓋結(jié)構(gòu)的安全性.?因多根拉索同時(shí)失效的概率較低,故本文僅探討單根拉索失效后屋蓋結(jié)構(gòu)的安全性.
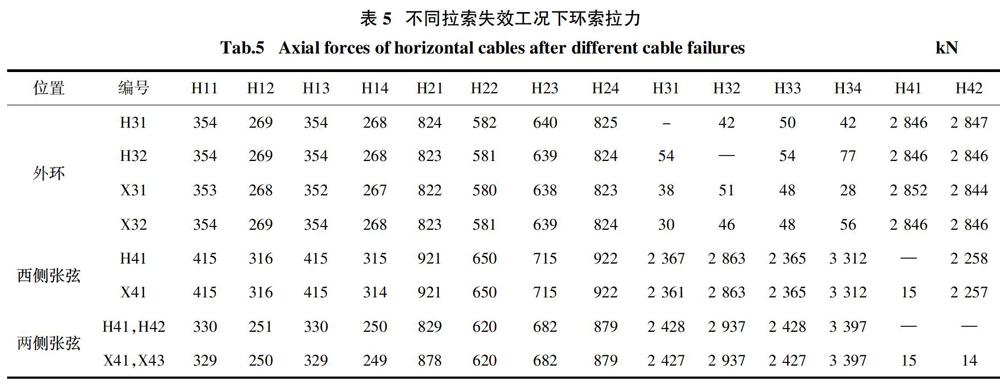
由表13、表14可知,完整屋蓋結(jié)構(gòu)中,不同位置(內(nèi)環(huán)、中環(huán)、外環(huán)、張弦)和不同布置形式(水平索和斜索)的拉索索力的絕對(duì)值差別較大.?因此,本文分析中探討了失效拉索位置和布置形式對(duì)剩余結(jié)構(gòu)響應(yīng)的影響.
以外環(huán)索為例,不同位置和布置形式的拉索失效后,剩余拉索索力值見表15.?從表1中可看出:當(dāng)外環(huán)中水平索或斜索失效后,外環(huán)中剩余拉索的索力僅50?kN左右(為拉索自重引起),說明同環(huán)中其余剩余拉索亦已失效.?即環(huán)索中任一拉索失效,會(huì)引起此環(huán)索整體(共8根拉索)全部失效.?因此,針對(duì)同一重環(huán)索,取任一拉索失效工況即可.?同樣地,張弦索中水平索或斜索失效,也會(huì)導(dǎo)致張弦索體系(共3根拉索)失效.?因此,針對(duì)張弦索,選擇任一拉索失效工況均可.
由于環(huán)索體系和張弦體系引起的失效拉索數(shù)量分別為8根和3根,數(shù)量相差較大.?為了更公平地比較“環(huán)索體系失效”和“張弦體系失效”對(duì)屋蓋結(jié)構(gòu)的影響,后文分析中增加“全部張弦索均失效”的分析工況,即“東、西兩側(cè)張弦索均失效”.
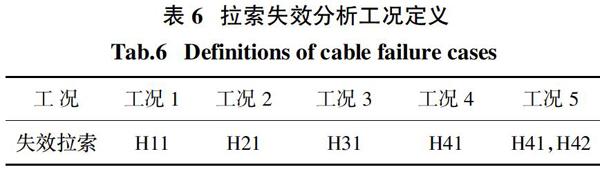
綜上所述,針對(duì)此結(jié)構(gòu)特點(diǎn),本文擬定的拉索失效的5種工況,見表16.
圖11所示為各重環(huán)索中水平索失效后的屋蓋豎向變形云圖.?可以看出:1)不同索失效后,引起不同程度的節(jié)點(diǎn)變形,從大到小依次為:工況3>工況4>工況1>工況2>工況5.?外環(huán)索失效的節(jié)點(diǎn)位移達(dá)到最大,為248?mm,為屋蓋短跨L的1/391,小于變形限值(L/250).?2)從變形云圖上看,不同索失效的屋蓋變形分布有較大差別.?為更細(xì)致地揭示不同拉索失效工況下屋蓋變形規(guī)律,本文分別選取屋蓋東西向和南北向關(guān)鍵節(jié)點(diǎn)的變形規(guī)律,如圖12所示.?同時(shí),為進(jìn)一步研究拉索體系對(duì)屋蓋結(jié)構(gòu)豎向剛度的貢獻(xiàn),圖12中還列出“僅上部網(wǎng)格梁屋蓋結(jié)構(gòu)”(后文簡(jiǎn)稱為“無索屋蓋”)的變形結(jié)果.
圖12(a)所示為不同拉索失效工況下東西向關(guān)鍵節(jié)點(diǎn)的撓度分布圖.?可以發(fā)現(xiàn):工況1、2、3中跨中撓度最大,逐漸向兩側(cè)減小,撓度曲線呈“U”形,與完整屋蓋和無索屋蓋的變形曲線一致.?工況5中跨中撓度顯著減小,東西兩側(cè)撓度增大,呈“W”形.?相比而言,工況4中西側(cè)撓度顯著增大,而東側(cè)撓度減小,呈“√”形.?產(chǎn)生此變形差異的原因是:工況4中僅一側(cè)張弦索失效后,另一側(cè)張弦索仍正常工作,因此,剩余屋蓋結(jié)構(gòu)在東西向?yàn)椴粚?duì)稱結(jié)構(gòu);對(duì)比而言,環(huán)索失效和兩側(cè)張弦梁失效后的剩余屋蓋結(jié)構(gòu)均為對(duì)稱結(jié)構(gòu),因此,屋蓋撓度曲線表1現(xiàn)為東西向?qū)ΨQ.
另外,值得注意的是:1)工況1、2、3中靠近支座位置的豎向變形值反而較“完整屋蓋”更小.?這是因?yàn)椋嬖谥T多撐桿的東西向屋蓋,可近似看成是“多點(diǎn)彈性支撐梁”.?當(dāng)跨中撓度增大時(shí),位于屋蓋兩端的節(jié)點(diǎn)則出現(xiàn)“變形反拱現(xiàn)象”.?2)工況4中屋蓋最大撓度大于工況5中的屋蓋最大撓度,這可能是因?yàn)楣r4中未失效一側(cè)張弦索產(chǎn)生的“反拱現(xiàn)象”加劇了失效一側(cè)的張弦梁處屋面撓度.
圖12(b)所示為不同拉索失效工況下南北向關(guān)鍵節(jié)點(diǎn)的撓度分布圖,可以發(fā)現(xiàn):
1)南北向“無索屋蓋”撓度曲線表1現(xiàn)為北側(cè)撓度大于南側(cè)撓度,最大撓度位于節(jié)點(diǎn)JS4處;而“完整屋蓋”撓度曲線表1現(xiàn)為對(duì)稱狀態(tài),最大撓度位于跨中節(jié)點(diǎn)處.?導(dǎo)致兩者變形曲線差異的原因是:結(jié)構(gòu)網(wǎng)格梁屋蓋的不等高設(shè)計(jì),使“無索屋蓋”在荷載作用下產(chǎn)生非對(duì)稱變形.?而在“完整屋蓋”中,即在“無索屋蓋”的基礎(chǔ)上增加拉索體系,從而改變屋面梁的豎向剛度,起到變形協(xié)調(diào)的作用.
2)工況1、4、5撓度曲線表1現(xiàn)為對(duì)稱分布,工況2、3撓度曲線表1現(xiàn)為非對(duì)稱分布.?產(chǎn)生這一現(xiàn)象的原因可以通過“完整屋蓋”和“無索屋蓋”的變形曲線比較得到解釋:中環(huán)索、外環(huán)索失效(工況2、工況3),剩余索的預(yù)加力十分有限,導(dǎo)致剩余屋蓋變形呈現(xiàn)類似“無索屋蓋”的非對(duì)稱變形特征.?而內(nèi)環(huán)索失效(工況1),僅索力較小的內(nèi)環(huán)索失效,剩余拉索預(yù)加力仍然很大,因此,其變形與“完整屋蓋”更為接近.
值得一提的是,工況4、工況5中屋蓋的跨中最大撓度小于完整屋蓋.?此現(xiàn)象可由“變形反拱現(xiàn)象”得到解釋.
3.3???拉索失效后的結(jié)構(gòu)內(nèi)力響應(yīng)
圖13所示為不同拉索失效工況下網(wǎng)格梁結(jié)構(gòu)的軸向應(yīng)力分布圖.?從中可看出:不同斷索工況下,外環(huán)斜索附近撐桿應(yīng)力最大,且由大到小排列為:工況3>工況2>工況1>工況4>工況5.?其中,工況3,即外環(huán)索失效時(shí),最大壓應(yīng)力達(dá)227?MPa,為完整屋蓋的1.78倍.
表17列出了不同拉索失效工況下,剩余結(jié)構(gòu)中關(guān)鍵拉索索力變化值.?從中可發(fā)現(xiàn):
內(nèi)環(huán)索(中環(huán)索)失效后(工況1、2),均不會(huì)引起剩余拉索索力的顯著增加.?相反,還會(huì)引起外環(huán)索和張弦索的索力下降,此現(xiàn)象可從屋蓋整體變形圖得到解釋(見圖13):當(dāng)內(nèi)環(huán)索(中環(huán)索)失效后,跨中撓度顯著增大,相應(yīng)地引起外環(huán)和張弦撐桿上端屋面梁產(chǎn)生“向上反拱”,最終,位于撓度反拱的網(wǎng)格梁下方的張弦索、外環(huán)索的索力下降.
外環(huán)索失效后(工況3),由于網(wǎng)格梁內(nèi)力傳遞作用,與其距離較近的張弦索的內(nèi)力增加約11.7%;但是,位于外環(huán)索內(nèi)部的內(nèi)環(huán)索和中環(huán)索的索力則有不同程度的下降,其中內(nèi)環(huán)索索力下降近31.6%.?因此,屋蓋變形圖上表1現(xiàn)為跨中撓度高達(dá)-223?mm.
僅西側(cè)張弦索失效時(shí),與其相鄰的外環(huán)索索力會(huì)略有增大,而中環(huán)、內(nèi)環(huán)索及西側(cè)張弦索的索力均減小;相比而言,當(dāng)兩側(cè)張弦索均失效時(shí),外環(huán)、中環(huán)、內(nèi)環(huán)的索力變化規(guī)律與單側(cè)拉索大致相同,但是變化數(shù)值約為后者的兩倍.
綜上所述,外環(huán)索和張弦索的失效會(huì)引起相鄰拉索索力不同程度地顯著增大,應(yīng)引起重視;同時(shí),外環(huán)索與張弦索的相互影響大于各環(huán)索之間的相互影響.
3.4???拉索失效后屋蓋的彈塑性極限承載力
對(duì)拉索失效后屋蓋結(jié)構(gòu)進(jìn)行考慮初始缺陷的雙重非線性極限承載力分析.?圖14給出了不同拉索失效工況下的屋蓋在施加初始缺陷后考慮幾何、材料雙重非線性的極限承載力(以“完整屋蓋的極限承載力”為基準(zhǔn)來表1示),可以看出:拉索失效對(duì)剩余屋蓋結(jié)構(gòu)極限承載力產(chǎn)生的影響由大到小依次為:外環(huán)索、張弦索、中環(huán)索、內(nèi)環(huán)索.?最不利工況為“外環(huán)索失效”:當(dāng)外環(huán)索失效時(shí)(工況3),剩余屋蓋極限承載力為36.2?MN,僅為完整屋蓋的65%.
值得注意的是:?jiǎn)蝹?cè)張弦索失效后剩余結(jié)構(gòu)的極限承載力為36.9?MN,小于兩側(cè)張弦索失效后剩余結(jié)構(gòu)的極限承載力(37.8?MN),說明單側(cè)張弦索失效會(huì)引起極限承載力更顯著的下降.?這一現(xiàn)象可以通過前文的“反拱現(xiàn)象”得以解釋.
4???結(jié)???論
通過SAP2000模擬多重四邊環(huán)索-張弦穹頂結(jié)構(gòu)的拉索失效,得到以下結(jié)論:
1)作為一種新型結(jié)構(gòu),多重四邊環(huán)索-張弦穹頂結(jié)構(gòu)外圈環(huán)索對(duì)結(jié)構(gòu)貢獻(xiàn)最大.?外環(huán)索失效對(duì)結(jié)構(gòu)節(jié)點(diǎn)位移、內(nèi)力、極限承載力各響應(yīng)的影響最大.
2)環(huán)索失效會(huì)引起整重環(huán)索失效,剩余結(jié)構(gòu)仍為對(duì)稱結(jié)構(gòu);張弦索失效僅引起單側(cè)張弦索全部失效,剩余結(jié)構(gòu)為非對(duì)稱結(jié)構(gòu).
3)拉索失效后,經(jīng)內(nèi)力重分布會(huì)增大部分桿件的內(nèi)力.?其中,外環(huán)索和張弦索的失效會(huì)引起相鄰拉索索力不同程度地顯著增大.?同時(shí),外環(huán)索與張弦索的相互影響大于各環(huán)索之間的相互影響,應(yīng)引起足夠重視.
4)不同位置的拉索失效會(huì)引起極限承載力不同程度的下降,降幅由大到小依次為:工況3>工況4?>工況5>工況2>工況1.
5)“單側(cè)張弦索失效”(3根拉索失效)引起的反拱現(xiàn)象,將導(dǎo)致“單側(cè)張弦索失效”比“兩側(cè)張弦索失效工況(6根拉索失效)”,更為不利.
6)不管是四邊環(huán)索體系,還是張弦索體系,均無多余的冗余度,為了提高此類結(jié)構(gòu)的安全儲(chǔ)備,建議采用一定的構(gòu)造措施增加拉索體系冗余度.
參考文獻(xiàn)
[1]????陳志華,劉紅波,王小盾,等.?弦支穹頂結(jié)構(gòu)研究綜述[J].?建筑結(jié)構(gòu)學(xué)報(bào),2010,31(S1):210—215.
CHEN?Z?H,LIU?H?B,WANG?X?D,et?al.?Review?and?forecast?of?suspendome?structures?[J].?Journal?of?Building?Structures,2010,31(S1):210—215.?(In?Chinese)
[2]????賀擁軍,孫軒,周緒紅.?張弦巨型網(wǎng)格結(jié)構(gòu)布索方案研究[J].?湖南大學(xué)學(xué)報(bào)(自然科學(xué)版),2015,42(5):8—13.
HE?Y?J,SUN?X,ZHOU?X?H.?Research?on?cable-strut?arrangement?of?string?reticulated?mega-structure?[J].?Journal?of?Hunan?University?(Natural?Sciences),2015,42(5):8—13.?(In?Chinese)
[3]????宗鐘凌,郭正興.?葵花型索穹頂結(jié)構(gòu)力學(xué)性能及拉索破斷試驗(yàn)研究[J].?工程力學(xué),2013,30(1):271—276.
ZONG?Z?L,GUO?Z?X.?Experimental?research?of?mechanical?properties?and?cable?broken?of?levy?cable?dome?[J].?Engineering?Mechanics,2013,30(1):271—276.?(In?Chinese)
[4]????SHEKASTENHBAND?B,ABEDI?K,DIANAT?N,et?al.?Experimental?and?numerical?studies?on?the?collapse?behavior?of?tensegrity?systems?considering?cable?rupture?and?strut?collapse?with?snap-through?[J].??????International?Journal?of?Non-linear?Mechanics,2012,47(7):751—768.
[5]????朱奕鋒,馮健,蔡建國(guó),等.??梅江會(huì)展中心張弦桁架抗連續(xù)倒塌分析[J].?建筑結(jié)構(gòu)學(xué)報(bào),2013,34(3):45—53.
ZHU?Y?F,F(xiàn)ENG?J,CAI?J?G,et?al.?Analysis?on?progressive?collapse?resistance?of?truss?string?structure?of?Meijiang?Exhibition?Center?[J].?Journal?of?Building?Structures,2013,34(3):45—53.?(In?Chinese)
[6]????王化杰,范峰,錢宏亮,等.?巨型網(wǎng)格弦支穹頂預(yù)應(yīng)力施工模擬分析與斷索研究[J].?建筑結(jié)構(gòu)學(xué)報(bào),2010,31(S1):247—253.
WANG?H?J,F(xiàn)AN?F,QIAN?H?L,et?al.?Analysis?of?pretensioning?construction?scheme?and?cable?breaking?for?megastructure?suspend-dome?[J].?Journal?of?Building?Structure,2010,31(S1):247—253.?(In?Chinese)
[7]????朱明亮,陸金鈺,郭正興.?新型環(huán)箍穹頂全張力結(jié)構(gòu)局部斷索抗連續(xù)倒塌性能分析[J].?東南大學(xué)學(xué)報(bào)(自然科學(xué)版),2016,46(5):1057—1062.
ZHU?M?L,LU?J?Y,GUO?Z?X.?Analysis?on?progressive?collapse?resistance?of?novel?torus-dome?tensile?structure?due?to?cable?rupture?[J].?Journal?of?Southeast?University(Natural?Science?Edition),2016,46(5):1057—1062.?(In?Chinese)
[8]????WANG?X?X,CHEN?Z?H,YU?Y?J,et?al.?Numerical?and?experimental?study?on?loaded?suspendome?subjected?to?sudden?cable?failure?[J].?Journal?of?Constructional?Steel?Research,2017,50(11):358—371.
[9]????HAN?Q?H,LIU?M?J,LU?Y,et?al.?Progressive?collapse?analysis?of?large-span?reticulated?domes?[J].?International?Journal?of?Steel?Structures,2015,15(2):261—269.
[10]??劉人杰,薛素鐸,李雄彥,等.?環(huán)形交叉索桁結(jié)構(gòu)局部斷索(桿)的動(dòng)力響應(yīng)分析[J].?工業(yè)建筑,2015,45(1):32—35.
LIU?R?J,XUE?S?D,LI?X?Y,et?al.?Dynamic?response?analysis?under?local?break?of?cable?or?rod?in?the?annular?crossed?cable-truss?structure?[J].?Industrial?Construction,2015,45(1):32—35.?(In?Chinese)
[11]??陸金鈺,董霄,李娜,等.?環(huán)箍-穹頂索桿結(jié)構(gòu)局部斷索抗倒塌能力分析[J].?工程力學(xué),2016,33(S1):173—178.
LU?J?Y,DONG?X,LI?N,et?al.?Progressive?collapse-resistant?capacity?analysis?of?torus-dome?cable-strut?structure?due?to?cablerupture?[J].?Engineering?Mechanics,2016,33(S1):173—178.?(In?Chinese)
[12]??姜正榮,劉小偉,石開榮,等.?索穹頂結(jié)構(gòu)桿破斷的敏感性分析[J].?華南理工大學(xué)學(xué)報(bào)(自然科學(xué)版),2017,45(5):90—96.
JIANG?Z?R,LIU?X?W,SHI?K?R,et?al.?Sensitivity?analysis?of?cable-strut?rupture?for?cable?dome[J].?Journal?of?South?China?University?of?Technology(Natural?Science?Edition),2017,45(5):90—96.?(In?Chinese)
[13]??高占遠(yuǎn),薛素鐸.?勁性支撐穹頂結(jié)構(gòu)局部斷索(桿)分析[J].?四川大學(xué)學(xué)報(bào)(工程科學(xué)版),2017,49(5):13—21.
GAO?Z?Y,XUE?S?D.?Analysis?of?rigid?bracing?dome?with?broken?cable(rod)?[J].?Sichuan?University?(Advanced?Engineering?Science),2017,49(5):13—21.?(In?Chinese)
[14]??張超,余立,許莉,等.?多重四邊環(huán)索-張弦穹頂屋蓋索力張拉方案比選[J].?福州大學(xué)學(xué)報(bào)(自然科學(xué)版),2017,45(2):151-158.
ZHANG?C,YU?L,XU?L,et?al.?Comparative?analysis?on?cable?tensioning?scheme?of?multiple?square?loops-string?dome?[J].?Journal?of?Fuzhou?University?(Natural?Science?Edition),2017,45(2):151—158.?(In?Chinese)
[15]??張超,余立,劉濤.?多重四邊形環(huán)索-張弦梁屋蓋拉索張拉施工過程監(jiān)測(cè)及數(shù)值模擬分析[J].?武漢理工大學(xué)學(xué)報(bào)(交通科學(xué)與工程版),2016,40(5):797—802.
ZHANG?C,YU?L,LIU?T.?Construction?process?monitoring?and?numerical?simulation?analysis?of?tensioning?of?multiple?square?loops-string?dome?[J].?Journal?of?Wuhan?University?of?Technology?(Transportation?Science?and?Engineering),2016,40(5):797—802.?(In?Chinese)
[16]??GB?50017—2003???鋼結(jié)構(gòu)設(shè)計(jì)規(guī)范[S].?北京:中國(guó)建筑工業(yè)出版社,2003:29-47.
GB?50017—2003???Code?for?steel?structures?[S].?Beijing:China?Architecture?and?Building?Press,2003:29—47.?(In?Chinese)
[17]??賀擁軍,彭正群.?蜂窩網(wǎng)格型球面網(wǎng)殼的非線性穩(wěn)定性研究[J].?湖南大學(xué)學(xué)報(bào)(自然科學(xué)版),2016,43(11):33—38.
HE?Y?J,PENG?Z?Q.?Nonlinear?stability?analysis?of?single-layer?honeycomb?spherical?latticed?shells?[J].?Journal?of?Hunan?University?(Natural?Sciences),2016,43(11):33—38.?(In?Chinese)
[18]??HE?S,JIANG?Z,CAI?J.?Investigation?on?simulation?methods?of?initial?geometric?imperfection?distribution?in?elasto-plastic?stability?analysis?of?single-layer?reticulated?shells[J].?KSCE?Journal?of?Civil?Engineering,2018,22(4):1193—1202.
[19]??崔曉強(qiáng),郭彥林.?Kiewit型弦支穹頂結(jié)構(gòu)的彈性極限承載力研究[J].?建筑結(jié)構(gòu)學(xué)報(bào),2003,24(1):74—79.
CUI?X?Q,GUO?Y?L.?Elastic?ultimate?capacity?of?Kiewitt?suspen-dome?[J].?Journal?of?Building?Structures,2003,24(1):74—79.?(In?Chinese)
[20]??KHUYEN?H?T,IWASAKI?E.?An?approximate?method?of?dynamic?amplification?factor?for?alternate?load?path?in?redundancy?and?progressive?collapse?linear?static?analysis?for?steel?truss?bridges?[J].?Case?Studies?in?Structural?Engineering,2016,6:53—62.
張超 付馨迪 許莉 顏學(xué)淵 賈宏宇



摘???要:多重四邊環(huán)索-張弦穹頂結(jié)構(gòu)作為一種新型的索支穹頂結(jié)構(gòu),拉索失效會(huì)對(duì)屋蓋結(jié)構(gòu)受力產(chǎn)生較大影響.?以全國(guó)首座三重四邊環(huán)索-張弦穹頂屋蓋(福州海峽奧林匹克中心體育館屋蓋)為研究背景,研究了拉索失效對(duì)于此類新型索支穹頂結(jié)構(gòu)的豎向剛度、構(gòu)件內(nèi)力及極限承載能力的影響規(guī)律,并評(píng)估單根拉索失效后屋蓋結(jié)構(gòu)的安全性.?分析結(jié)果表1明:拉索失效均會(huì)引起屋蓋顯著下?lián)希鞣N工況中外環(huán)索失效會(huì)引起最大的屋蓋下?lián)希牵煌魇Ш笪萆w豎向變形分布規(guī)律相差較大;外環(huán)索和張弦索的失效會(huì)引起相鄰拉索索力不同程度的增大;外環(huán)索與張弦索的相互影響大于各環(huán)索之間的相互影響;不同位置的拉索失效均會(huì)引起屋蓋極限承載能力下降,外環(huán)索失效引起結(jié)構(gòu)極限承載力下降最顯著;“僅單側(cè)張弦索失效”會(huì)引起較“兩側(cè)張弦索均失效”更不利的屋蓋撓度和極限承載力.?總之,外環(huán)索失效為最不利拉索失效工況,會(huì)引起屋蓋最大撓度增大134%,張弦索索力增加11.7%,極限承載力減小35%.?但是,剩余整體屋蓋結(jié)構(gòu)仍具有一定的安全性.
關(guān)鍵詞:多重環(huán)索;張弦梁;穹頂;拉索失效;極限承載能力
中圖分類號(hào):TU356???????????????????????文獻(xiàn)標(biāo)志碼:A
Influence?of?Multiple?Square?Loops-string?Dome?Subjected?to?Cable?Failure
ZHANG?Chao1,2,F(xiàn)U?Xindi1,XU?Li1,YAN?Xueyuan1?,JIA?Hongyu3
(1.?College?of?Civil?Engineering,F(xiàn)uzhou?University,F(xiàn)uzhou?350108,China;
2.?Key?Laboratory?of?Urban?Security?&?Disaster?Engineering?(Beijing?University?of?Technology)?of?the?MOE,Beijing?100124,China;
3.?School?of?Civil?Engineering,Southwest?Jiaotong?University,Chengdu?610031,China)
Abstract:Multiple?square?loops-string?dome?is?a?newly?suspen-dome?structure,and?cable?failure?shows?significant?effect?on?multiple?square?loops-string?dome?structures.?This?paper?used?the?Fuzhou?Strait?Olympic?Center?Gymnasium?as?the?research?background?to?study?the?effect?of?cable?on?the?vertical?stiffness?of?the?roof,the?internal?forces?of?the?roof?and?the?ultimate?bearing?capacity,and?safety?capability?evaluation?of?the?cable?failure?roof?was?carried?out.?The?analysis?results?show?that?the?vertical?deformation?of?the?roof?can?be?reduced?after?cable?failure.?Among?them,the?failure?of?the?outer?loop?cable?causes?the?maximum?vertical?deformation.?However,various?vertical?deformation?distributions?subjected?to?different?cable?failure?are?generated.?The?failure?of?either?the?outer?loop?or?string?cable?can?increase?the?tension?force?of?the?adjacent?cable?significantly.?The?interaction?between?the?outer?loop?cable?and?string?cable?is?greater?than?the?mutual?influence?between?the?other?loop?cables;?Ultimate?bearing?capacity?of?the?roof?can?be?reduced?when?cable?failure?occurs,which?reaches?the?minimum?value?when?the?outer?loop?cable?fails.?It?should?be?noted?that?“Only?one?side?string?cable?failure”?causes?more?serious?deflection?and?less?ultimate?bearing?capacity?when?compared?with“two?side?string?cable?failure”.?In?all,failure?of?the?outer?loop?cable?is?the?most?serious?case,which?causes?that?vertical?deflection?increases?by?134%,the?cable?tension?force?of?adjacent?cable?increases?by?11.7%,and?the?ultimate?bearing?capacity?reduces?by?35%.?However,the?residual?roof?structure?is?still?in?a?safe?state.
Key?words:multiple?square?loops;beam?string;domes;cable?failure;ultimate?bearing?capacity
弦支穹頂結(jié)構(gòu)是由日本政法大學(xué)川口衛(wèi)教授于1993年提出的一種新型雜交空間結(jié)構(gòu)[1],具有造型美觀、節(jié)省材料、質(zhì)量輕、剛度大、抗震性能好等空間結(jié)構(gòu)的綜合優(yōu)勢(shì),在大型的公共與工業(yè)建筑中得到廣泛應(yīng)用.?典型的工程應(yīng)用包括日本前橋綠色會(huì)館、日本北九州穴生屋頂、濟(jì)南奧體中心體育館、常州體育館、2008年北京奧運(yùn)會(huì)羽毛球館等.
1963年1月,羅馬尼亞布加勒斯特市一座直徑為93?m的國(guó)家經(jīng)濟(jì)展覽館穹頂網(wǎng)殼在近1?m厚積雪作用下失穩(wěn)倒塌.?此后,網(wǎng)殼結(jié)構(gòu)的安全問題成為人們研究的熱點(diǎn).?索結(jié)構(gòu)屬于柔性結(jié)構(gòu)體系,預(yù)應(yīng)力的引入可顯著改善網(wǎng)格結(jié)構(gòu)的整體變形、桿件內(nèi)力峰值和整體穩(wěn)定承載力[2].雖然在索穹頂結(jié)構(gòu)設(shè)計(jì)中,拉索的設(shè)計(jì)應(yīng)力只取索強(qiáng)度的30%~50%,且均采用強(qiáng)度較高的鋼材,不容易發(fā)生破斷,但實(shí)際使用過程中依然會(huì)因材料質(zhì)量缺陷、維護(hù)缺陷、加工和施工缺陷等偶然因素引起某根索的破斷,造成結(jié)構(gòu)整體性垮塌.
對(duì)于預(yù)應(yīng)力索桿結(jié)構(gòu)的斷索安全性,國(guó)內(nèi)外學(xué)者已開展了相關(guān)研究,如索穹頂[3]、張拉整體[4]、張弦桁架[5]、弦支穹頂[6-9]、索桿結(jié)構(gòu)[10-13]等.?朱明亮等[7]對(duì)一種由周邊環(huán)形張拉整體和中部索穹頂組成的新型環(huán)箍-穹頂全張力結(jié)構(gòu)進(jìn)行靜力和動(dòng)力分析,發(fā)現(xiàn)張拉整體單元的拉索破斷主要影響所在單元附近拉索,不會(huì)形成連續(xù)倒塌.?姜正榮等[12]對(duì)Levy型索穹頂結(jié)構(gòu)索桿破斷進(jìn)行敏感性分析,發(fā)現(xiàn)Levy型索穹頂對(duì)環(huán)索和中心撐桿的破斷最為敏感,其中最外環(huán)圈環(huán)索破斷對(duì)應(yīng)的敏感性系數(shù)最大.?高占遠(yuǎn)等[13]運(yùn)用瞬態(tài)動(dòng)力學(xué)的Newmark時(shí)間積分法對(duì)單根索桿斷裂后結(jié)構(gòu)的力學(xué)性能進(jìn)行分析,并提出一種桿件重要系數(shù),發(fā)現(xiàn)外環(huán)桿的重要性排在首位,內(nèi)脊索排在末位.?然而,目前對(duì)于拉索失效影響的分析僅是針對(duì)傳統(tǒng)弦支穹頂結(jié)構(gòu),由多重四邊環(huán)索、張弦索組合形成的復(fù)雜弦支穹頂屋蓋,各重拉索體系的受力相互影響,某局部拉索失效后,剩余拉索體系(同一環(huán)索中剩余拉索及其他重環(huán)索)會(huì)進(jìn)行復(fù)雜的內(nèi)力重分布,對(duì)于屋蓋結(jié)構(gòu)的影響規(guī)律可能會(huì)顯著區(qū)別于傳統(tǒng)索穹頂結(jié)構(gòu).?因此,本文以全國(guó)首個(gè)三重四邊環(huán)索-張弦索組合穹頂屋蓋——福州海峽奧林匹克中心體育館工程為研究背景,研究可能發(fā)生的拉索失效對(duì)于此類新型索支穹頂屋蓋結(jié)構(gòu)的剛度、內(nèi)力、穩(wěn)定極限承載能力的影響規(guī)律,并評(píng)估單根拉索斷裂后屋蓋結(jié)構(gòu)的安全性.
1???工程背景及數(shù)值模型
1.1???工程背景
福州海峽奧林匹克中心體育館屋蓋采用多重四邊環(huán)索-張弦穹頂結(jié)構(gòu),由網(wǎng)格梁、撐桿、斜索、四邊形環(huán)索、張弦梁構(gòu)成,其中各層撐桿與網(wǎng)格梁和索的連接均為鉸接.?屋蓋跨度約97?m?×?116?m,周圍混凝土柱作為屋蓋結(jié)構(gòu)的內(nèi)支座,弦支結(jié)構(gòu)網(wǎng)格梁與支座剛接,網(wǎng)格梁采用矩形截面鋼管.?為保證屋蓋結(jié)構(gòu)的空間幾何穩(wěn)定性,并避免壓桿側(cè)向失穩(wěn),本結(jié)構(gòu)在網(wǎng)格梁中設(shè)置十字交叉形和V形兩種形式的屋面支撐,采用圓形截面鋼管.?屋蓋網(wǎng)格梁、撐桿、支撐等型鋼構(gòu)件均采用Q345,混凝土柱采用C40.?此屋蓋結(jié)構(gòu)東西方向?qū)ΨQ,北側(cè)屋蓋標(biāo)高高于南側(cè),且北側(cè)網(wǎng)格梁橫向跨度略大于南側(cè)網(wǎng)格梁.
三重四邊環(huán)索成矩形,第一環(huán)(內(nèi)環(huán))撐桿高度9.0?m,四邊形環(huán)索長(zhǎng)21.6?m、19.0?m,斜索長(zhǎng)13.9?m、15.0?m;第二環(huán)(中環(huán))撐桿9.0?m,四邊形環(huán)索長(zhǎng)37.9?m、36.0?m,斜索長(zhǎng)13.4?m、14.85?m;第三環(huán)(外環(huán))撐桿9.5?m,四邊形環(huán)索長(zhǎng)56.9?m、51.1?m,斜索長(zhǎng)度15.8?m、18.2?m.?為增加豎向剛度,在四邊形環(huán)索第三環(huán)增設(shè)中間撐桿,高13.0?m,在東西兩側(cè)設(shè)置獨(dú)立張弦結(jié)構(gòu),撐桿高度8.5?m、11.0?m,索規(guī)格及相關(guān)參數(shù)見表11.
1.2???三維數(shù)值模型建立
本文采用SAP2000建立三維空間數(shù)值模型,如圖1所示.?其中,網(wǎng)格梁為箱型截面,屋面支撐為圓形截面鋼管,均采用Frame單元模擬,鋼材彈性模量為206?GPa;預(yù)應(yīng)力拉索采用Cable單元模擬,拉索彈性模量為195?GPa.?“型鋼混凝土環(huán)梁”和“混凝土柱”均采用Frame單元模擬,截面特性均按照實(shí)際截面計(jì)算;根據(jù)環(huán)梁與混凝土柱剛接的實(shí)際情況,數(shù)值模型中,混凝土柱頂節(jié)點(diǎn)與環(huán)梁節(jié)點(diǎn)剛接;混凝土柱底則為固端約束.
(c)屋蓋變形監(jiān)測(cè)節(jié)點(diǎn)
圖2???關(guān)鍵構(gòu)件編號(hào)示意圖
Fig.2???Numbering?diagram?of?key?components
1.3???基準(zhǔn)數(shù)值模型驗(yàn)證
為驗(yàn)證本文所建數(shù)值模型的準(zhǔn)確性,按實(shí)際屋蓋施工過程中拉索張拉情況,定義非線性階段施工工況,采用短鏈桿的溫降收縮[14]模擬索力張拉過程,得到不同索力張拉過程中各監(jiān)測(cè)關(guān)鍵點(diǎn)的受力及變形.?監(jiān)測(cè)關(guān)鍵點(diǎn)布置情況如圖3(a)、圖4(a)所示.
圖3(b)、圖4(b)分別表1示網(wǎng)格梁應(yīng)力和屋蓋節(jié)點(diǎn)撓度的實(shí)測(cè)數(shù)據(jù)與模型計(jì)算結(jié)果的對(duì)比.?從圖3(b)中可看出,實(shí)測(cè)數(shù)據(jù)與模型計(jì)算結(jié)果相差較小,誤差最大的為16號(hào),實(shí)測(cè)數(shù)據(jù)與模型計(jì)算值相差16.1?MPa.?從圖4(b)中可看出,實(shí)測(cè)數(shù)據(jù)的撓度值略小于模型計(jì)算值,但兩者相差較小,誤差最大的為6號(hào)節(jié)點(diǎn),二者相差10.1?mm.?由于篇幅有限,其監(jiān)測(cè)結(jié)果對(duì)比詳見文獻(xiàn)[15].
總之,各施工階段的數(shù)值模擬結(jié)果與實(shí)際施工監(jiān)測(cè)數(shù)據(jù)總體吻合較好,誤差均在可接受的范圍內(nèi).?因此,本文在后續(xù)分析中,以此數(shù)值模型為基準(zhǔn)分析模型.
2???完整屋蓋結(jié)構(gòu)的響應(yīng)規(guī)律
2.1???變形及內(nèi)力響應(yīng)
在上節(jié)基準(zhǔn)數(shù)值模型的基礎(chǔ)上,健康狀態(tài)下的完整屋蓋結(jié)構(gòu)(后文簡(jiǎn)稱“完整屋蓋”,以區(qū)分于拉索失效后屋蓋結(jié)構(gòu))在實(shí)際運(yùn)營(yíng)過程中,應(yīng)考慮屋面蓋板等二期附加恒載以及屋蓋活荷載的組合作用,其中,附加恒載為0.823?kN/m2,活載為0.5?kN/m2.?本文按“1.0附加恒載+1.0活載”考慮正常使用階段的荷載組合.
在正常使用階段荷載組合作用下,完整屋蓋的變形和軸向應(yīng)力如圖5、圖6所示,其中跨中節(jié)點(diǎn)位移最大,達(dá)106?mm,小于規(guī)范[16]規(guī)定屋蓋跨中撓度控制值388?mm?(L/250,L為完整屋蓋短跨).?外環(huán)斜索附近屋面支撐的壓應(yīng)力最大,約為127?MPa,但小于Q345鋼材的抗壓強(qiáng)度設(shè)計(jì)值f?(310?MPa).
豎向撐桿可看作是兩端鉸接的軸心受壓構(gòu)件.?本屋蓋體系中各類型撐桿軸壓力及截面應(yīng)力見表12.?根據(jù)《鋼結(jié)構(gòu)設(shè)計(jì)規(guī)范》[16]需要對(duì)受壓構(gòu)件進(jìn)行強(qiáng)度承載力和穩(wěn)定承載力驗(yàn)算.?根據(jù)穩(wěn)定承載力驗(yàn)算,截面應(yīng)力應(yīng)小于φf.?其中,f為鋼材的軸心受壓強(qiáng)度,設(shè)計(jì)值為310?MPa;φ為軸壓構(gòu)件穩(wěn)定系數(shù),根據(jù)構(gòu)件的長(zhǎng)細(xì)比、鋼材屈服強(qiáng)度和截面分類按規(guī)范[16]中附錄C采用.?穩(wěn)定性驗(yàn)算結(jié)果見表13,所有豎向撐桿的穩(wěn)定承載力滿足設(shè)計(jì)要求,并有一定的富余度.
表13、表14分別為各個(gè)位置的水平拉索及斜索索力分布.?可以看出:各重環(huán)的索力分布基本呈對(duì)稱狀
態(tài),南北向的索力均大于東西向的索力;同一重環(huán)的斜索索力大于環(huán)索索力;索力從內(nèi)環(huán)到外環(huán)依次增大,水平索中,H34索力最大,達(dá)到3?192?kN,小于其對(duì)應(yīng)的破斷荷載(13?412?kN);斜索中,X34索力最大,達(dá)到4?348?kN,遠(yuǎn)小于其對(duì)應(yīng)的破斷荷載(216?58?kN).
2.2???極限承載能力
一般認(rèn)為,弦支穹頂結(jié)構(gòu)中的單層網(wǎng)殼屬于缺陷敏感性結(jié)構(gòu),其臨界荷載可能會(huì)因極小的初始幾何缺陷而大大降低.?同時(shí),文獻(xiàn)[17]發(fā)現(xiàn)單層蜂窩型球面網(wǎng)殼因受到初始缺陷影響,其極限承載力不斷下降.?因此本文采用一致缺陷模態(tài)法[18]來考慮屋蓋的初始缺陷.?其中,初始缺陷按第一階整體線性屈曲模態(tài)分布方式(如圖7所示),表1現(xiàn)為:沿南北向屋蓋豎向?qū)ΨQ振動(dòng),沿東西向屋蓋豎向反對(duì)稱振動(dòng).?缺陷最大值按屋蓋短跨跨度(L)的1/300選取.
為探討完整屋蓋的極限承載力,本文在對(duì)完整屋蓋施加初始缺陷后,進(jìn)行考慮幾何、材料雙重非線性的彈塑性極限承載力分析.?在彈塑性數(shù)值模型中,網(wǎng)格梁兩端設(shè)置彎矩鉸,屋面支撐和豎向撐桿設(shè)置軸力鉸來模擬材料非線性.?其中,以1#網(wǎng)格梁為例(見圖2(c)),列出計(jì)算的彎矩鉸的彎矩-曲率曲線如圖8所示;計(jì)算得到的2#屋面支撐(見圖2(c))軸力鉸的力-位移曲線如圖9所示.?圖8和圖9中,點(diǎn)B代
圖10給出了完整屋蓋的極限承載力-位移曲線,為對(duì)比材料非線性的影響,對(duì)結(jié)構(gòu)在考慮初始缺陷基礎(chǔ)上進(jìn)行彈塑性分析的同時(shí),還進(jìn)行了僅考慮幾何非線性的彈性分析[19].?可看出:完整屋蓋的彈性極限承載力為66.7?MN,彈塑性極限承載力為56.1?MN.?說明彈性極限承載力會(huì)過高地估計(jì)屋蓋結(jié)構(gòu)承載力.?因此,后文計(jì)算屋蓋結(jié)構(gòu)極限承載力時(shí)均考慮屋蓋結(jié)構(gòu)的幾何、材料雙重非線性因素的影響.
3???拉索失效后屋蓋結(jié)構(gòu)的響應(yīng)規(guī)律
3.1???拉索失效分析工況研究
本文數(shù)值分析中,采用變換荷載路徑法[20]模擬拉索失效,即基于完整屋蓋結(jié)構(gòu)的數(shù)值模型,通過“移除”相應(yīng)的失效單元,得到拉索失效后的屋蓋結(jié)構(gòu),進(jìn)一步分析拉索失效后屋蓋結(jié)構(gòu)的變形響應(yīng)、內(nèi)力分布及極限承載力,進(jìn)而評(píng)估拉索失效后屋蓋結(jié)構(gòu)的安全性.?因多根拉索同時(shí)失效的概率較低,故本文僅探討單根拉索失效后屋蓋結(jié)構(gòu)的安全性.
由表13、表14可知,完整屋蓋結(jié)構(gòu)中,不同位置(內(nèi)環(huán)、中環(huán)、外環(huán)、張弦)和不同布置形式(水平索和斜索)的拉索索力的絕對(duì)值差別較大.?因此,本文分析中探討了失效拉索位置和布置形式對(duì)剩余結(jié)構(gòu)響應(yīng)的影響.
以外環(huán)索為例,不同位置和布置形式的拉索失效后,剩余拉索索力值見表15.?從表1中可看出:當(dāng)外環(huán)中水平索或斜索失效后,外環(huán)中剩余拉索的索力僅50?kN左右(為拉索自重引起),說明同環(huán)中其余剩余拉索亦已失效.?即環(huán)索中任一拉索失效,會(huì)引起此環(huán)索整體(共8根拉索)全部失效.?因此,針對(duì)同一重環(huán)索,取任一拉索失效工況即可.?同樣地,張弦索中水平索或斜索失效,也會(huì)導(dǎo)致張弦索體系(共3根拉索)失效.?因此,針對(duì)張弦索,選擇任一拉索失效工況均可.
由于環(huán)索體系和張弦體系引起的失效拉索數(shù)量分別為8根和3根,數(shù)量相差較大.?為了更公平地比較“環(huán)索體系失效”和“張弦體系失效”對(duì)屋蓋結(jié)構(gòu)的影響,后文分析中增加“全部張弦索均失效”的分析工況,即“東、西兩側(cè)張弦索均失效”.
綜上所述,針對(duì)此結(jié)構(gòu)特點(diǎn),本文擬定的拉索失效的5種工況,見表16.
圖11所示為各重環(huán)索中水平索失效后的屋蓋豎向變形云圖.?可以看出:1)不同索失效后,引起不同程度的節(jié)點(diǎn)變形,從大到小依次為:工況3>工況4>工況1>工況2>工況5.?外環(huán)索失效的節(jié)點(diǎn)位移達(dá)到最大,為248?mm,為屋蓋短跨L的1/391,小于變形限值(L/250).?2)從變形云圖上看,不同索失效的屋蓋變形分布有較大差別.?為更細(xì)致地揭示不同拉索失效工況下屋蓋變形規(guī)律,本文分別選取屋蓋東西向和南北向關(guān)鍵節(jié)點(diǎn)的變形規(guī)律,如圖12所示.?同時(shí),為進(jìn)一步研究拉索體系對(duì)屋蓋結(jié)構(gòu)豎向剛度的貢獻(xiàn),圖12中還列出“僅上部網(wǎng)格梁屋蓋結(jié)構(gòu)”(后文簡(jiǎn)稱為“無索屋蓋”)的變形結(jié)果.
圖12(a)所示為不同拉索失效工況下東西向關(guān)鍵節(jié)點(diǎn)的撓度分布圖.?可以發(fā)現(xiàn):工況1、2、3中跨中撓度最大,逐漸向兩側(cè)減小,撓度曲線呈“U”形,與完整屋蓋和無索屋蓋的變形曲線一致.?工況5中跨中撓度顯著減小,東西兩側(cè)撓度增大,呈“W”形.?相比而言,工況4中西側(cè)撓度顯著增大,而東側(cè)撓度減小,呈“√”形.?產(chǎn)生此變形差異的原因是:工況4中僅一側(cè)張弦索失效后,另一側(cè)張弦索仍正常工作,因此,剩余屋蓋結(jié)構(gòu)在東西向?yàn)椴粚?duì)稱結(jié)構(gòu);對(duì)比而言,環(huán)索失效和兩側(cè)張弦梁失效后的剩余屋蓋結(jié)構(gòu)均為對(duì)稱結(jié)構(gòu),因此,屋蓋撓度曲線表1現(xiàn)為東西向?qū)ΨQ.
另外,值得注意的是:1)工況1、2、3中靠近支座位置的豎向變形值反而較“完整屋蓋”更小.?這是因?yàn)椋嬖谥T多撐桿的東西向屋蓋,可近似看成是“多點(diǎn)彈性支撐梁”.?當(dāng)跨中撓度增大時(shí),位于屋蓋兩端的節(jié)點(diǎn)則出現(xiàn)“變形反拱現(xiàn)象”.?2)工況4中屋蓋最大撓度大于工況5中的屋蓋最大撓度,這可能是因?yàn)楣r4中未失效一側(cè)張弦索產(chǎn)生的“反拱現(xiàn)象”加劇了失效一側(cè)的張弦梁處屋面撓度.
圖12(b)所示為不同拉索失效工況下南北向關(guān)鍵節(jié)點(diǎn)的撓度分布圖,可以發(fā)現(xiàn):
1)南北向“無索屋蓋”撓度曲線表1現(xiàn)為北側(cè)撓度大于南側(cè)撓度,最大撓度位于節(jié)點(diǎn)JS4處;而“完整屋蓋”撓度曲線表1現(xiàn)為對(duì)稱狀態(tài),最大撓度位于跨中節(jié)點(diǎn)處.?導(dǎo)致兩者變形曲線差異的原因是:結(jié)構(gòu)網(wǎng)格梁屋蓋的不等高設(shè)計(jì),使“無索屋蓋”在荷載作用下產(chǎn)生非對(duì)稱變形.?而在“完整屋蓋”中,即在“無索屋蓋”的基礎(chǔ)上增加拉索體系,從而改變屋面梁的豎向剛度,起到變形協(xié)調(diào)的作用.
2)工況1、4、5撓度曲線表1現(xiàn)為對(duì)稱分布,工況2、3撓度曲線表1現(xiàn)為非對(duì)稱分布.?產(chǎn)生這一現(xiàn)象的原因可以通過“完整屋蓋”和“無索屋蓋”的變形曲線比較得到解釋:中環(huán)索、外環(huán)索失效(工況2、工況3),剩余索的預(yù)加力十分有限,導(dǎo)致剩余屋蓋變形呈現(xiàn)類似“無索屋蓋”的非對(duì)稱變形特征.?而內(nèi)環(huán)索失效(工況1),僅索力較小的內(nèi)環(huán)索失效,剩余拉索預(yù)加力仍然很大,因此,其變形與“完整屋蓋”更為接近.
值得一提的是,工況4、工況5中屋蓋的跨中最大撓度小于完整屋蓋.?此現(xiàn)象可由“變形反拱現(xiàn)象”得到解釋.
3.3???拉索失效后的結(jié)構(gòu)內(nèi)力響應(yīng)
圖13所示為不同拉索失效工況下網(wǎng)格梁結(jié)構(gòu)的軸向應(yīng)力分布圖.?從中可看出:不同斷索工況下,外環(huán)斜索附近撐桿應(yīng)力最大,且由大到小排列為:工況3>工況2>工況1>工況4>工況5.?其中,工況3,即外環(huán)索失效時(shí),最大壓應(yīng)力達(dá)227?MPa,為完整屋蓋的1.78倍.
表17列出了不同拉索失效工況下,剩余結(jié)構(gòu)中關(guān)鍵拉索索力變化值.?從中可發(fā)現(xiàn):
內(nèi)環(huán)索(中環(huán)索)失效后(工況1、2),均不會(huì)引起剩余拉索索力的顯著增加.?相反,還會(huì)引起外環(huán)索和張弦索的索力下降,此現(xiàn)象可從屋蓋整體變形圖得到解釋(見圖13):當(dāng)內(nèi)環(huán)索(中環(huán)索)失效后,跨中撓度顯著增大,相應(yīng)地引起外環(huán)和張弦撐桿上端屋面梁產(chǎn)生“向上反拱”,最終,位于撓度反拱的網(wǎng)格梁下方的張弦索、外環(huán)索的索力下降.
外環(huán)索失效后(工況3),由于網(wǎng)格梁內(nèi)力傳遞作用,與其距離較近的張弦索的內(nèi)力增加約11.7%;但是,位于外環(huán)索內(nèi)部的內(nèi)環(huán)索和中環(huán)索的索力則有不同程度的下降,其中內(nèi)環(huán)索索力下降近31.6%.?因此,屋蓋變形圖上表1現(xiàn)為跨中撓度高達(dá)-223?mm.
僅西側(cè)張弦索失效時(shí),與其相鄰的外環(huán)索索力會(huì)略有增大,而中環(huán)、內(nèi)環(huán)索及西側(cè)張弦索的索力均減小;相比而言,當(dāng)兩側(cè)張弦索均失效時(shí),外環(huán)、中環(huán)、內(nèi)環(huán)的索力變化規(guī)律與單側(cè)拉索大致相同,但是變化數(shù)值約為后者的兩倍.
綜上所述,外環(huán)索和張弦索的失效會(huì)引起相鄰拉索索力不同程度地顯著增大,應(yīng)引起重視;同時(shí),外環(huán)索與張弦索的相互影響大于各環(huán)索之間的相互影響.
3.4???拉索失效后屋蓋的彈塑性極限承載力
對(duì)拉索失效后屋蓋結(jié)構(gòu)進(jìn)行考慮初始缺陷的雙重非線性極限承載力分析.?圖14給出了不同拉索失效工況下的屋蓋在施加初始缺陷后考慮幾何、材料雙重非線性的極限承載力(以“完整屋蓋的極限承載力”為基準(zhǔn)來表1示),可以看出:拉索失效對(duì)剩余屋蓋結(jié)構(gòu)極限承載力產(chǎn)生的影響由大到小依次為:外環(huán)索、張弦索、中環(huán)索、內(nèi)環(huán)索.?最不利工況為“外環(huán)索失效”:當(dāng)外環(huán)索失效時(shí)(工況3),剩余屋蓋極限承載力為36.2?MN,僅為完整屋蓋的65%.
值得注意的是:?jiǎn)蝹?cè)張弦索失效后剩余結(jié)構(gòu)的極限承載力為36.9?MN,小于兩側(cè)張弦索失效后剩余結(jié)構(gòu)的極限承載力(37.8?MN),說明單側(cè)張弦索失效會(huì)引起極限承載力更顯著的下降.?這一現(xiàn)象可以通過前文的“反拱現(xiàn)象”得以解釋.
4???結(jié)???論
通過SAP2000模擬多重四邊環(huán)索-張弦穹頂結(jié)構(gòu)的拉索失效,得到以下結(jié)論:
1)作為一種新型結(jié)構(gòu),多重四邊環(huán)索-張弦穹頂結(jié)構(gòu)外圈環(huán)索對(duì)結(jié)構(gòu)貢獻(xiàn)最大.?外環(huán)索失效對(duì)結(jié)構(gòu)節(jié)點(diǎn)位移、內(nèi)力、極限承載力各響應(yīng)的影響最大.
2)環(huán)索失效會(huì)引起整重環(huán)索失效,剩余結(jié)構(gòu)仍為對(duì)稱結(jié)構(gòu);張弦索失效僅引起單側(cè)張弦索全部失效,剩余結(jié)構(gòu)為非對(duì)稱結(jié)構(gòu).
3)拉索失效后,經(jīng)內(nèi)力重分布會(huì)增大部分桿件的內(nèi)力.?其中,外環(huán)索和張弦索的失效會(huì)引起相鄰拉索索力不同程度地顯著增大.?同時(shí),外環(huán)索與張弦索的相互影響大于各環(huán)索之間的相互影響,應(yīng)引起足夠重視.
4)不同位置的拉索失效會(huì)引起極限承載力不同程度的下降,降幅由大到小依次為:工況3>工況4?>工況5>工況2>工況1.
5)“單側(cè)張弦索失效”(3根拉索失效)引起的反拱現(xiàn)象,將導(dǎo)致“單側(cè)張弦索失效”比“兩側(cè)張弦索失效工況(6根拉索失效)”,更為不利.
6)不管是四邊環(huán)索體系,還是張弦索體系,均無多余的冗余度,為了提高此類結(jié)構(gòu)的安全儲(chǔ)備,建議采用一定的構(gòu)造措施增加拉索體系冗余度.
參考文獻(xiàn)
[1]????陳志華,劉紅波,王小盾,等.?弦支穹頂結(jié)構(gòu)研究綜述[J].?建筑結(jié)構(gòu)學(xué)報(bào),2010,31(S1):210—215.
CHEN?Z?H,LIU?H?B,WANG?X?D,et?al.?Review?and?forecast?of?suspendome?structures?[J].?Journal?of?Building?Structures,2010,31(S1):210—215.?(In?Chinese)
[2]????賀擁軍,孫軒,周緒紅.?張弦巨型網(wǎng)格結(jié)構(gòu)布索方案研究[J].?湖南大學(xué)學(xué)報(bào)(自然科學(xué)版),2015,42(5):8—13.
HE?Y?J,SUN?X,ZHOU?X?H.?Research?on?cable-strut?arrangement?of?string?reticulated?mega-structure?[J].?Journal?of?Hunan?University?(Natural?Sciences),2015,42(5):8—13.?(In?Chinese)
[3]????宗鐘凌,郭正興.?葵花型索穹頂結(jié)構(gòu)力學(xué)性能及拉索破斷試驗(yàn)研究[J].?工程力學(xué),2013,30(1):271—276.
ZONG?Z?L,GUO?Z?X.?Experimental?research?of?mechanical?properties?and?cable?broken?of?levy?cable?dome?[J].?Engineering?Mechanics,2013,30(1):271—276.?(In?Chinese)
[4]????SHEKASTENHBAND?B,ABEDI?K,DIANAT?N,et?al.?Experimental?and?numerical?studies?on?the?collapse?behavior?of?tensegrity?systems?considering?cable?rupture?and?strut?collapse?with?snap-through?[J].??????International?Journal?of?Non-linear?Mechanics,2012,47(7):751—768.
[5]????朱奕鋒,馮健,蔡建國(guó),等.??梅江會(huì)展中心張弦桁架抗連續(xù)倒塌分析[J].?建筑結(jié)構(gòu)學(xué)報(bào),2013,34(3):45—53.
ZHU?Y?F,F(xiàn)ENG?J,CAI?J?G,et?al.?Analysis?on?progressive?collapse?resistance?of?truss?string?structure?of?Meijiang?Exhibition?Center?[J].?Journal?of?Building?Structures,2013,34(3):45—53.?(In?Chinese)
[6]????王化杰,范峰,錢宏亮,等.?巨型網(wǎng)格弦支穹頂預(yù)應(yīng)力施工模擬分析與斷索研究[J].?建筑結(jié)構(gòu)學(xué)報(bào),2010,31(S1):247—253.
WANG?H?J,F(xiàn)AN?F,QIAN?H?L,et?al.?Analysis?of?pretensioning?construction?scheme?and?cable?breaking?for?megastructure?suspend-dome?[J].?Journal?of?Building?Structure,2010,31(S1):247—253.?(In?Chinese)
[7]????朱明亮,陸金鈺,郭正興.?新型環(huán)箍穹頂全張力結(jié)構(gòu)局部斷索抗連續(xù)倒塌性能分析[J].?東南大學(xué)學(xué)報(bào)(自然科學(xué)版),2016,46(5):1057—1062.
ZHU?M?L,LU?J?Y,GUO?Z?X.?Analysis?on?progressive?collapse?resistance?of?novel?torus-dome?tensile?structure?due?to?cable?rupture?[J].?Journal?of?Southeast?University(Natural?Science?Edition),2016,46(5):1057—1062.?(In?Chinese)
[8]????WANG?X?X,CHEN?Z?H,YU?Y?J,et?al.?Numerical?and?experimental?study?on?loaded?suspendome?subjected?to?sudden?cable?failure?[J].?Journal?of?Constructional?Steel?Research,2017,50(11):358—371.
[9]????HAN?Q?H,LIU?M?J,LU?Y,et?al.?Progressive?collapse?analysis?of?large-span?reticulated?domes?[J].?International?Journal?of?Steel?Structures,2015,15(2):261—269.
[10]??劉人杰,薛素鐸,李雄彥,等.?環(huán)形交叉索桁結(jié)構(gòu)局部斷索(桿)的動(dòng)力響應(yīng)分析[J].?工業(yè)建筑,2015,45(1):32—35.
LIU?R?J,XUE?S?D,LI?X?Y,et?al.?Dynamic?response?analysis?under?local?break?of?cable?or?rod?in?the?annular?crossed?cable-truss?structure?[J].?Industrial?Construction,2015,45(1):32—35.?(In?Chinese)
[11]??陸金鈺,董霄,李娜,等.?環(huán)箍-穹頂索桿結(jié)構(gòu)局部斷索抗倒塌能力分析[J].?工程力學(xué),2016,33(S1):173—178.
LU?J?Y,DONG?X,LI?N,et?al.?Progressive?collapse-resistant?capacity?analysis?of?torus-dome?cable-strut?structure?due?to?cablerupture?[J].?Engineering?Mechanics,2016,33(S1):173—178.?(In?Chinese)
[12]??姜正榮,劉小偉,石開榮,等.?索穹頂結(jié)構(gòu)桿破斷的敏感性分析[J].?華南理工大學(xué)學(xué)報(bào)(自然科學(xué)版),2017,45(5):90—96.
JIANG?Z?R,LIU?X?W,SHI?K?R,et?al.?Sensitivity?analysis?of?cable-strut?rupture?for?cable?dome[J].?Journal?of?South?China?University?of?Technology(Natural?Science?Edition),2017,45(5):90—96.?(In?Chinese)
[13]??高占遠(yuǎn),薛素鐸.?勁性支撐穹頂結(jié)構(gòu)局部斷索(桿)分析[J].?四川大學(xué)學(xué)報(bào)(工程科學(xué)版),2017,49(5):13—21.
GAO?Z?Y,XUE?S?D.?Analysis?of?rigid?bracing?dome?with?broken?cable(rod)?[J].?Sichuan?University?(Advanced?Engineering?Science),2017,49(5):13—21.?(In?Chinese)
[14]??張超,余立,許莉,等.?多重四邊環(huán)索-張弦穹頂屋蓋索力張拉方案比選[J].?福州大學(xué)學(xué)報(bào)(自然科學(xué)版),2017,45(2):151-158.
ZHANG?C,YU?L,XU?L,et?al.?Comparative?analysis?on?cable?tensioning?scheme?of?multiple?square?loops-string?dome?[J].?Journal?of?Fuzhou?University?(Natural?Science?Edition),2017,45(2):151—158.?(In?Chinese)
[15]??張超,余立,劉濤.?多重四邊形環(huán)索-張弦梁屋蓋拉索張拉施工過程監(jiān)測(cè)及數(shù)值模擬分析[J].?武漢理工大學(xué)學(xué)報(bào)(交通科學(xué)與工程版),2016,40(5):797—802.
ZHANG?C,YU?L,LIU?T.?Construction?process?monitoring?and?numerical?simulation?analysis?of?tensioning?of?multiple?square?loops-string?dome?[J].?Journal?of?Wuhan?University?of?Technology?(Transportation?Science?and?Engineering),2016,40(5):797—802.?(In?Chinese)
[16]??GB?50017—2003???鋼結(jié)構(gòu)設(shè)計(jì)規(guī)范[S].?北京:中國(guó)建筑工業(yè)出版社,2003:29-47.
GB?50017—2003???Code?for?steel?structures?[S].?Beijing:China?Architecture?and?Building?Press,2003:29—47.?(In?Chinese)
[17]??賀擁軍,彭正群.?蜂窩網(wǎng)格型球面網(wǎng)殼的非線性穩(wěn)定性研究[J].?湖南大學(xué)學(xué)報(bào)(自然科學(xué)版),2016,43(11):33—38.
HE?Y?J,PENG?Z?Q.?Nonlinear?stability?analysis?of?single-layer?honeycomb?spherical?latticed?shells?[J].?Journal?of?Hunan?University?(Natural?Sciences),2016,43(11):33—38.?(In?Chinese)
[18]??HE?S,JIANG?Z,CAI?J.?Investigation?on?simulation?methods?of?initial?geometric?imperfection?distribution?in?elasto-plastic?stability?analysis?of?single-layer?reticulated?shells[J].?KSCE?Journal?of?Civil?Engineering,2018,22(4):1193—1202.
[19]??崔曉強(qiáng),郭彥林.?Kiewit型弦支穹頂結(jié)構(gòu)的彈性極限承載力研究[J].?建筑結(jié)構(gòu)學(xué)報(bào),2003,24(1):74—79.
CUI?X?Q,GUO?Y?L.?Elastic?ultimate?capacity?of?Kiewitt?suspen-dome?[J].?Journal?of?Building?Structures,2003,24(1):74—79.?(In?Chinese)
[20]??KHUYEN?H?T,IWASAKI?E.?An?approximate?method?of?dynamic?amplification?factor?for?alternate?load?path?in?redundancy?and?progressive?collapse?linear?static?analysis?for?steel?truss?bridges?[J].?Case?Studies?in?Structural?Engineering,2016,6:53—62.

