基于ARMA模型預測我國貨幣供應量M1

張雨 許學軍

摘 要：貨幣供應量M1作為一個重要的先行指標，反映了經濟周期和價格的波動。嚴密監測與調控貨幣供應量M1對抑制通貨膨脹和促進經濟健康增長具有重要的意義。因此，正確預測貨幣供應量M1的變動顯得尤為重要。以我國貨幣供應量M1從2018年4月至2020年4月的月度數據為樣本，通過Eviews統計軟件，構建貨幣供應量的ARMA模型，經檢驗擬合效果較好且模型預測誤差較小，最后利用該模型對未來3個月（2020年5—7月）的貨幣供應量M1進行預測。

關鍵詞：時間序列;ARMA模型;貨幣供應量

中圖分類號：F820? ? ? ? 文獻標志碼：A? ? ? 文章編號：1673-291X（2020）36-0052-03

引言

貨幣供應量M1反映了貨幣供給的活化程度，其與經濟的微觀預期及經濟的基本面息息相關。其作為經濟基本面的領先指標，引起了人們的高度重視和廣泛研究。貨幣供應量作為一個時間序列，數據之間具有合乎規律的連續性。在一定條件下，如果未來期間整體的經濟環境沒有發生巨大的變化，貨幣供應量的基本發展趨勢還會延續下去，所以可以建模來分析其中的規律。

ARMA模型是研究時間序列平穩隨機過程的典型方法，將此模型運用到貨幣供應量M1的預測，可以降低預測誤差。因此，本文以貨幣供應量M1的歷史數據為樣本，通過建立ARMA模型預測未來3個月的貨幣供應量M1。

一、模型理論介紹

（一）ARMA模型簡介

自回歸移動平均模型ARMA主要應用于對一維、方差恒定的時間序列進行分析，認為時間序列當年觀測項的值可以表示為之前的p項觀測值及q項隨機誤差的線性組合，如式（1）所示，記作ARMA（p，q）模型。

其中，Xt與前p期的序列值有關，還與前q期的隨機干擾有關，εt為噪聲，稱時間序列{Xt}為p階自回歸移動平均模型。p是自回歸階數，q是移動平均階數，Φi（i=1，2，…，p）是自回歸參數，θj（j=1，2，…，p）是移動平均參數。

（二）ARMA模型的平穩性檢驗

當時間序列不平穩時，不能直接運用ARMA模型。因此收集和預處理數據之后，要對數據進行平穩性檢驗。對ARMA模型進行平穩性檢驗常用的方法是單位根（ADF）檢驗法。首先對式（2）進行回歸分析：

根據回歸分析的結果，分析ADF檢驗的t統計量和其所對應的P值，如果P值在相應的置信區間內顯著，就表明可以拒絕原假設，認為該時間序列是平穩的。反之，若不能拒絕原假設，就可以判斷該時間序列是非平穩的，此時要對數據進行處理使其平穩。

（三）ARMA模型的類型和滯后階數

ARMA模型的具體類型是依據（偏）自相關系數的形態決定。若時間序列的偏自相關系數與其自相關系數都呈現拖尾形態，則可以使用ARMA（p，q）建立模型，并可以根據（偏）自相關系數粗略的估計滯后階數。當根據相關系數難以確定p和q滯后的階數時，需要結合信息準則來判斷。即當p和q達到某一組數值時，AIC（p，q）、SC（p，q）和HQ（p，q）達到最小值時的p和q為最佳的模型階數。

二、我國貨幣供應量M1的實證分析及預測

（一）數據選取

本文以我國貨幣供應量M1從2018年4月至2020年4月的月度數據作為樣本，數據來源于東方財富網數據中心。通過Eviews統計軟件，運用ARMA模型構建了關于貨幣供應量M1的預測分析模型。

（二）數據的單位根檢驗

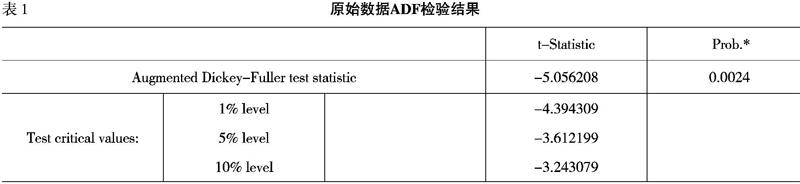
數據的平穩性檢驗是建立模型的基礎，檢驗平穩性經常使用的是單位根（ADF）檢驗法。使用Eviews統計軟件對原始數據進行單位根檢驗（如下頁表1所示），ADF檢驗的t統計量小于1%顯著性水平下的臨界值，故該序列數據是平穩的，可以利用此數據建立模型。

（三）識別模型形式

在驗證原始數據是平穩的時間序列之后，我們需要觀察自相關和偏自相關系數圖來識別模型的形式，并結合信息準則判斷模型的滯后階數。

從下圖左側可以看出，貨幣供應量M1的自相關和偏自相關都具有拖尾的形態，初步確定可以使用ARMA模型對貨幣供應量M1進行預測分析，同時結合信息準則來進一步預測該模型的滯后階數。

由于樣本（偏）自相關系數在滯后一階的時候明顯超過兩倍標準差的界限，但從滯后兩階開始幾乎所有的（偏）自相關系數都在界限之內，所以暫時粗略的估計滯后兩階。又因為通常情況下，ARMA模型的滯后階數不會太大，故選取ARMA（1，1）、ARMA（1，2）、ARMA（2，1）、ARMA（2，2）這四種情形進行回歸分析，結果（如表2所示）。根據信息準則，比較AIC（p，q）、SC（p，q）、HQ（p，q）的值可以得出，p=1和q=1為最佳的模型階數，此時的ARMA（1，1）為最佳的模型。

同時，觀察ARMA（1，1）回歸分析的結果（如下頁表3所示），各系數都在99%的置信區間內顯著，所以我們選ARMA（1，1）模型對我國貨幣供應量M1進行建模。

（四）建立模型

結合信息準則和回歸分析的結果可以確定擬合度較好的預測模型是ARMA（1，1）。從下頁表3回歸分析的結果中可以得知，該模型的參數估計值中AR（1）的t統計量為15.69476，其對應的P值為0.00;MA（1）的t統計量為-16.62485，其對應的P值為0.00，都在99%的置信區間內顯著，因此其對應的模型表達式為：

Xt=29625.3755+0.9487Xt-1+εt-0.9479εt

接下來，對ARMA（1，1）回歸模型進行殘差檢驗，從回歸方程的殘差圖中可以得出，均方誤差度較小，殘差序列樣本的絕對值與均方誤差區間差異較小。因此可以認為，模型ARMA（1，1）估計結果的殘差序列不存在自相關。

（五）模型預測

對擬合模型2019年10月至2020年4月的數據進行靜態預測，得出曲線均在有效區間內，且模型預測值基本和差分序列圖擬合。進一步驗證，本文建立的模型較為準確，可以運用此模型進行預測。最后，通過ARMA（1，1）模型對未來3個月貨幣供應量M1進行模型差分預測，預測差距值的相對變動率在3%之內。經計算調整后，暫估未來3個月貨幣供應量M1（以億元為單位）依次為573 630、562 500、584 640。

結語

本文利用時間序列分析的建模思想，對我國貨幣供應量這一時間序列進行實證分析。本文的整體思路如下：首先，對樣本序列進行平穩性檢驗，在保證平穩性的基礎上，根據相關系數和信息準則來估計模型的滯后階數。其次，利用最小二乘法估計模型的參數，并檢驗殘差是否存在自相關。最后，通過擬合預測值和實際值驗證模型的可靠性，并以此來預測未來3個月的貨幣供應量M1。

綜上所述，ARMA模型充分利用有限的數據集對未來的發展趨勢進行了預測分析。通過ARMA模型進行建模和實證分析得到的短期貨幣供應量M1的預測值較為理想，為學者分析經濟周期和價格波動提供了一定的參考意義。

參考文獻：

[1]? 張思奇，馬剛，冉華.股票市場風險、收益與市場效率：——ARMA-ARCH-M模型[J].世界經濟，2000，（5）：19-28.

[2]? 郭雪，王彥波.基于ARMA模型對滬市股票指數的預測[J].Economic&TradeUpdate，2006，（4）：58-59.

[3]? 李美威，謝小鵬，馮偉，賀石中.基于ARMA模型的在線油液監測故障預警研究[J].潤滑與密封，2019，（12）：108-113.

[4]? 陳易平，俞龍，諶頏.大數據環境下基于小波神經網絡和ARMA模型的流量異常檢測[J].重慶理工大學學報：自然科學版，2019，（10）：149-154.

[5]? 蔡承智，黃軍結，梁穎.基于ARIMA模型的世界大豆總產預測分析[J].大豆科學，2019，（2）：298-303.

[6]? 鄧軍，楊宣，王瑋，等.運用ARMA模型對股價預測的市政研究[J].企業導報，2010，（6）：266-267.

[7]? 徐晨萌，方華.運用ARMA模型對股價預測的實證研究[J].經濟研究導刊，2019，（31）：77-82.