淺談定積分教學的優化策略

廣東省廣州市增城中學 侯曉燕

新課改后，在高中階段加入定積分的知識，擴大了學生學習的知識面，減少了在求解不規則平面圖形面積問題時的運算量，也為學有余力的同學提供了進一步學習的途徑和機會。縱觀近10 年高考全國卷，雖然每年的高考理科數學考試大綱對定積分與微積分原理的要求基本不變，但僅在2010 年考查了定積分概念及簡單運算，2011 年考查了定積分應用求面積，2012 年至今未見一題。近10 年高考考核新增熱點、難點，從算法到線性回歸直線方程，從二項分布與超幾何分布近似代替到獨立性檢驗，從熱點時事到數學文化知識成為題目背景，對定積分的考查也很有可能成為新的熱門考點，所以如何在有限的教學時間里完成考綱要求，培養學生進入大學后學習定積分的興趣，對定積分進行優化教學，還是值得研究的課題。

一、定積分概念教學及微積分基本原理的引入

以計算面積為索引，以分割求和為突破口，結合求極限思想，引入定積分概念。

物理求解運動位移，目前只能解決勻速直線運動，勻變速直線運動，如果一旦是一般的變速運動呢？

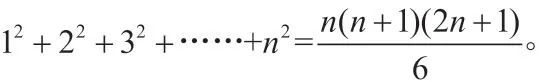
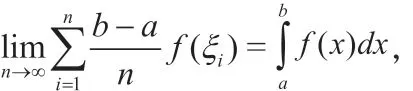
微積分基本定理揭示了導數和定積分之間的聯系，同時也提供了計算定積分的一種有效方法。微積分基本定理揭示了導數和定積分之間的聯系，同時也提供了計算定積分的一種有效方法。學生在經歷煩瑣的概念運算及數列求和過程中產生的消極情緒有了突破口，一下子精神振奮，很好奇地想知道解決方法，于是順理成章地引入課本45頁定積分概念，并利用微積分基本原理進行運算，而且在變式教學中，教師要不斷培養學生的思維轉換能力，“一題多變”對學生的知識能力進行了鞏固性訓練，增添了學生在學習過程中的趣味性，喚醒了學生的求知欲望，促使學生樂于研究此類題型。

通過比較，學生積累了利用微積分基本原理解決定積分的運算興趣，并為后面的運算題及理解定積分的幾何意義打下基礎。

二、定積分的幾何意義

在學生掌握好定積分運算后，方進入定積分幾何意義的學習。這樣的后置安排，有利于定積分幾何意義的探索，同樣能調動學生的數學思維，鍛煉數形結合解決數學問題的能力。同時，基于“最近發展區理論”，在教學中找準學生的認知起點，確定這節課教學的起點和終點，指引學生達到相應的層次，盡可能發揮潛能。

例2：（課本P53 例2）計算下列定積分：

【教師點撥】 通過計算發現，定積分有正有負。而我們為計算曲邊梯形面積引入了定積分，問題出現在哪里？引導學生查閱課本選修中定積分的幾何意義，得出P54 的結論：當對應的曲邊梯形位于軸上方時，定積分的值取正值，且等于曲邊梯形面積；當對應的曲邊梯形位于 軸下方時，定積分的值取負值，且等于曲邊梯形面積的相反數。

變式訓練1：已知函數 的圖像如下圖所示，則陰影部分的面積 為（ ）

例3：計算下列定積分。

【教師點撥】例3 是應用定積分的幾何意義，把數的問題用圖形來呈現，用求圖形面積來解決定積分計算的問題，其中（1）～（5）題對應的圖形分別是：

方法2：數形結合，計算陰影部分梯形面積。

（2）分段函數積分，數形結合，化繁為簡。

（4）綜合考查學生的應變能力，定積分基本運算及數形結合能力。

（5）在（3）的基礎上，考查學生的應變能力，數形結合能力，割補法求面積。

在這個知識點的教學設計里，變式教學，一法多用，是對解決問題的方法加以總結與歸納，進而形成一種技巧的解題方式。通過這種技巧的學習可以達到多題歸一的目的，使學生能夠迅速抓住題型的本質，將所學知識與能力的培養有機結合起來，提升課堂教學效率，并有助于學生良好學習習慣的養成，拓展學生思維的廣度。

三、定積分的綜合應用

高考數學試題中難題有一類題目題干較長，文字較多，會設計一些背景材料，在考試時間緊張的情況下會對考生心理造成很大壓力。例如定積分的應用，主要分為兩大類：一是定積分在幾何中的應用，二是定積分在物理中的應用，又分為變速運動、力學做功。這兩類應用課本及參考書已經有大量的例題及練習。在這里補充的是定積分與其他知識點結合的題。

A. 6+2sin2 B. -6-2sin2 C.20 D.-20

（5）概率：如圖，在邊長為e（e為自然對數的底數）的正方形區域的A處與C處各有一個通信基站，其信號覆蓋范圍分別為如圖所示的陰影區域，該正方形區域內無其他信號來源，且這兩個基站工作正常。若在該正方形區域內隨機選擇一個地點，則該地點無信號的概率為( )

A. 33 B.46 C.48 D. 50

高考數學命題思路是在考查基礎知識的基礎上，注重對數學思想方法的考查，注重對數學能力的考查，展現數學的科學價值和人文價值，同時兼顧試題的基礎性、綜合性和應用性。雖然定積分內容不多，但是可以與其他各章知識點結合考查學生的數學素養，應該給予重視。本文只是對定積分教學做了幾點優化嘗試，更多的優化值得教師們去探索研究。