復合建模在高樁透空式防波堤工程的研究與實踐

高 峰，郭源媛，許雄文，張慈珩，管 寧 ，彭 程

(1.交通運輸部天津水運工程科學研究所 港口水工建筑物技術國家工程實驗室 工程泥沙交通行業重點實驗室，天津 300456；2.天津大學 建筑工程學院，天津 300392；3.中交第三航務工程勘察設計院有限公司，上海 200032；4.三亞市交通運輸局，三亞 572099)

復合建模(Composite Modeling)不是一種全新的試驗技術，20世紀70年代即在海岸工程和水利工程中出現了這種新興的模擬技術，這是將物理模型與數學模型結合在一起的新模型，標志著模擬技術方面的重大進展。最先是由德國 Hannvoer大學的 Holz[1]提出了這種模型，其將一長段河道分成兩小段，分別用物模和數模各模擬其中一段，并通過接口耦合同步，加拿大學者將Holz的試驗結果首先應用到圣勞倫斯河口整體模型中。隨后，這種建模方法不斷發展應用，Oumeraci H[2]在海岸工程物理模擬中開展了數值模擬和現場測量的協同效應研究，Kamphuis J W[3]在第27屆國際海岸工程會議中就提出復合模型建模設計，Van Os A G，Soulsby R S和Kirkegaard J[4]探索了歐洲水力學研究中實驗方法的未來作用。如今高速大容量計算資源的提升使得數值模擬成為更受歡迎的工程研究手段，但是傳統物理測試仍然是必要補充，正是由于海岸工程設計中存在較大的不確定性，實測數據不完整、不充分和現有手段并不十分完善，導致一些實際問題和模擬過程很難用單一的數值方法求解。同樣，基于不斷的物理模型試驗的結果積累，更加參數化的描述方法也將納入數值模型中不斷提升數模技術的進步，兩者相互嵌套、相輔相成。廣義的復合建模是集成現場測量、數值模擬、試驗室研究和理論分析等各種研究方法，以獲得更好的解決方案，特別是對于不同空間尺度的復雜問題，其建模能力更高，是單個物理模型或數值模型所不能做到的。單個研究方法無法充分再現海岸工程問題所涉及的復雜過程，更不能以一種方法取代所有其他方法。一般最常用的方法是將物理模型和數值模型相結合，這是一種非常穩定的技術。復核建模的基本思路即是在更經濟的空間和成本條件下，先以數值模型基于1:1比例的精確建模，預測全球范圍或大尺度的水動力過程，被用作建模的第一階段，并作為物模的一種較為便捷的補充方法，快速提供設計所需的參數，而物理模型的邊界條件則來自數值模型，物模研究專注于解決小尺度的局部問題，并更直觀地理解和復演更加復雜的水動力過程，將一個非常復雜的海岸工程問題分解成幾個更容易分析和跟蹤的過程，這些過程可以用最合適的方法來描述，以獲得更可靠的結果。

海岸工程中的防波堤主要作用是擋浪，波浪在堤前破碎或反射，建筑物依靠自重來承受巨大的波浪荷載而維持穩定，因而傳統實體堤身高大、造價較高，且對生態環境影響較大。近年來，隨著經濟社會的發展，人們對海洋防護工程建設的觀念也大有不同，人們對環境的重視，綠色環保型、可持續發展型的工程越來越受到青睞。如今的港口建設不僅需要防波堤具有防浪功能，還需要防波堤滿足海洋生態環境的要求。因此，研究消波性能好、安全穩定且滿足環保要求的新型防波堤結構已迫在眉睫。在此背景下，透空式防波堤應運而生，基于波浪理論的研究和試驗表明，波動主要集中在水體上層，在表層2～3 倍波高的水層厚度內集中了90%以上的波能，由樁墩結構和入水一定深度的擋浪結構所組成的透空式防波堤就是根據這個特點設計[5]。上部擋浪結構可衰減外海傳來的大部分波浪，而在下部允許水體通過。由于透空式防波堤利于港內水體循環交換、對地質條件要求低等優點，特別適用于對環境有特殊要求的近海港口工程，既可達到較好的掩護效果，又可保證港區內具有良好的水質條件，而透空式防波堤的消波性能研究也是這一類型結構研究的重點問題之一。目前，國內外學者在板式透空式防波堤的水動力特性方面取得了一定的研究成果，在防波堤的結構形式上主要是以水平板或豎直板為主，主要通過交錯遮掩、渦流磨擦、沿程吸收、衰減、耗散波能，從而達到減小通過堤后的傳遞波高[6-7]。本文研究依托具體某海上巴士碼頭工程，針對其高樁透空式防波堤兼顧碼頭的結構形式進行專題試驗研究，結合數值模擬和物理模型的復合建模試驗研究方法，對透浪特性等設計參數進行測試驗證，為設計方案的確定提供科學依據。

1 消浪機理與研究思路

1.1 依托工程概況

圖1 高樁透空防波堤兼碼頭結構斷面示意圖(尺寸：mm)

該工程擬在開敞海域新建2個客輪泊位和預留2個游船泊位，由于受所在地海洋保護和海域環境的使用要求限制，不能采用傳統的斜坡式防波堤進行港區掩護。因此，在碼頭東側通過1座透空式棧橋與后方陸域連接，該碼頭即采用高樁結構形式兼做透空式防波堤，港內側布置橡膠護舷及系船柱用于停泊，外側布置擋浪板以一定深度入水，其剖面結構型式示意如圖1所示。

1.2 消浪原理

不同結構型式的透空式防波堤由于結構型式的差異，其消浪機理也有所差別。依托工程(圖1)為直立擋板透空式防波堤結構形式，主要是通過直立擋板反射波能及擋板斷面壓縮和板端出現渦漩消耗能量外，還有波浪通過擋板開孔形成渦漩耗能等措施。主要通過交錯遮掩、沿程吸收、衰減、耗散波能，使水體與擋板結構間碰撞或產生渦流磨擦,逐級消耗能量，從而達到減小通過堤后的傳遞波高，使堤后透射波高相對較小。透空式防波堤的消浪效果通常采用波浪透射率Kt來表征，波浪透射率Kt越小，堤后波高Ht就愈小，防波堤的消浪效果越好。國外學者已從理論上對透空式防波堤的波浪透射率進行研究與探索，如Ursell[8]首先研究無限水深時直立擋板的波浪透射率,給出深水條件下的精確解，Wiegel[9]假設透射波能量等于擋板下的入射波能量，用微幅波理論推導出了有限水深情況下波浪透射率的近似解。Hayashi[10]從連續方程和Berno ulli定理出發，假設堤前波浪為長波，堤前波浪水質點速度沿水深均勻分布,推導出圓柱型垂直樁防波堤的波浪透射率的計算公式。國內外對于透空式防波堤消浪特性的研究，除上述典型情況采用理論研究外，多數還是采用模型試驗方法研究。同時，由于各種透空式防波堤結構多樣復雜，消浪機理也有所差異，但都是從能量耗散的觀點出發與分析的，通過多次改變水質點的運動方向，使之相互碰撞或產生渦流，逐級消耗波能,從而既減小堤前反射波高，實現減小堤后透射波高[11]。

1.3 研究思路

由于高樁透空式防波堤的透浪系數與結構形式密切相關，傳統平面二維數值模型中對這類結構往往概化處理，如增加局部底摩阻系數或改變地形等，需要根據經驗判斷入射波透浪衰減并確定折減系數。相對而言物理模型則更為直觀，但需要一定場地、較大成本與時間，同時還有比尺效應。為了充分發揮數模、物模各自的優勢，復合模型正是通過數、物模之間交換數據使得兩種不同的試驗方法融合為一個整體，從而得到所需要的試驗成果，實現研究目的高效方法。本文先后采用二維數值波浪水槽與平面二維波浪數模、波浪水槽與局部三維波浪物理模型組成的多重復合建模方法開展研究。首先由平面二維整體波浪數模確定防波堤設計波浪要素和后續研究的波浪場邊界條件，再由數值波浪水槽初步確定正向入射波的透浪系數后再供平面波浪數模估算泊位損失作業天數，進而通過二維波浪水槽進行透浪系數的驗證并測試結構波浪力與越浪情況，最后考慮到數模對于復雜結構很難同時兼顧透射、繞射與反射等波浪傳播特性的模擬，故再以三維局部物理模型試驗進行對比驗證，從而在檢驗和修正不同浪向下的投射系數的同時，分析堤后碼頭泊穩條件，進而分析損失作業天數。

2 數值模擬方法與成果分析

2.1 數學模型試驗

根據已經驗證的工程外海-45 m等深線處重現期波浪條件，在自然地形條件下即工程建設前，推算工程區設計波浪條件，同時為工程后波浪場計算提供邊界條件。該模式為基于求解拋物型緩坡方程的PMS波浪數學模型，并在此基礎上進一步通過基于Boussinesq方程的BW近岸折射繞射數學模型，模擬工程建設后的港區波浪場分布，為分析碼頭泊穩條件和損失作業天數提供依據。其中，大范圍PMS波浪模型Kirby在Pade基礎上完善和發展的拋物型緩坡方程，可用于較大傳播角度的波浪計算，傳播主方向為x的方程為

(1)

模型中為了減少誤差保證計算的精確度，計算中均采用正向入射即入射方向與方程傳播的主方向x向相同。

圖2為PMS模型計算范圍與BW港區模型的嵌套關系以及極端高水位重現期為100 a時的H13%波高(圖2-a)和對應BW模型中港區范圍比波高分布(圖2-b)結果。結果表明，本工程主要控制浪向為S向，其次為SSE和SSW、SW向。其中，PMS模型推算的設計波浪要素結果也用作小范圍BW港區模型的起始波浪條件。

擬建工程防波堤處主要位于-1.6～-5.0 m水深水域，計算得到控制波浪S向H13%波高在2.53～4.55 m，其他浪向作用下SSE為2.24～3.86 m、SSW向為2.50～4.46 m和SW向為2.48～4.41 m。在PMS模型的基礎上，通過BW模型進一步計算工程建設后受防波堤掩護條件下設計高水位S向浪重現期2 a碼頭前沿波高，以分析泊位處的泊穩條件，此時平面二維波浪數模中的透空式防波堤透浪系數采用了后文中提到的二維水槽以及物理模型的試驗結果。

2-a 重現期100 a H13%波高2-b 港區比波高分布

2.1.2 二維波浪數值水槽

鑒于影響消浪效果的因素眾多，而復雜結構的透空防波堤暫無成熟的經驗估算方法，因此在數模階段采用CFD數值模型確定的透射系數來率定空隙介質的孔隙率。本研究依托FLOW-3D波浪模型，以RANS方程及連續性方程作為控制方程，通過VOF方法追蹤自由表面，可模擬復雜結構與波浪的相互作用[12]。由于控制方程為基礎的質量守恒及動量守恒方程，無需率定即可給出可靠的計算結果，其控制方程如下

連續性方程

首先，高校應積極利用自身的科研優勢，縱向開掘，深入研究并大力傳承中國傳統文化。幾千年的歷史長河孕育了輝煌燦爛的中華文明，這是祖先留給我們的寶貴財富。姑且單以易學一脈而言：研究《周易》的名家學者代不乏人，他們傾其心力，從不同的視角潛玩易學并為其作注訓疏。因此，易學已不僅僅是占算吉兇的卜筮之學，它更涵蓋了哲學、經濟管理、軍事、醫學等社會人生的方方面面。因為古代典籍保存方法落后和經歷時間太過久遠等諸多原因，許多珍貴的資料已經亡佚，現存的典籍也多有舛訛。所以，要完善協同創新體系，繁榮發展哲學社會科學事業，我們首先必須要深入挖掘、科學梳理、充分利用、積極傳承中華傳統文化中的優秀成分。

(2)

動量方程式

(3)

式中：ρ為流體密度，VF是可流動的體積分數，Ax、Ay、Az代表著x、y、z三個方向可流動的面積分數，u、v、w為對應x、y、z的速度分量；Gx、Gy、Gz為物體在x、y、z三個方向的重力加速度；fx、fy、fz為三個方向的粘滯力加速度。

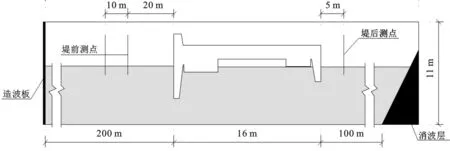
圖3 二維數值波浪水槽示意圖

湍流模型采用k-ε模型，自由表面采用VOF法進行追蹤，即通過求解方程獲取自由表面位置。

提取前文二維平面波浪數學模型中擬建防波堤處的波浪要素作為數值波浪水槽試驗的率波邊界條件，建立如圖3所示的二維數值波浪水槽，長348 m、高11 m、寬2.0 m。計算網格尺寸為：長0.2 m、高0.05 m、寬0.2 m。水槽左端采用與波浪條件相適應的非線性生波邊界，右端設置消波層。波浪條件及透射系數計算結果如表1所示，可見擋浪板擋浪效果與水位相關：水位越高，擋浪效果越好。

表1 二維數模得到的透射系數計算結果

2.2 物理模型試驗

在前面研究的基礎上，為進一步確定和復核防波堤/碼頭平面與結構布置，開展物理模型試驗驗證工作，包括：(1)二維水槽斷面試驗，主要針對透空式結構形式，校核與補充不同擋浪板底高程在設計高水位不同波浪作用下堤防的透射系數，并對防波堤結構所受波浪力進行測試；(2)三維局部整體試驗波浪，主要對不同波向時透空式防波堤在波浪作用下的傳播特征以及泊穩條件進行驗證。

表2 二維波浪物模得到的透射系數計算結果

2.2.1 二維波浪斷面物模

結合場地與技術要求，采用正態模型，幾何比尺20，即水深比尺、波高比尺、波長比尺均為20，周期比尺為4.47，力比尺為8 000。為便于驗證，率波邊界條件與數值波浪水槽一致。試驗中針對透空式結構，確定不同擋浪板底高程(-2.0 m和-3.0 m)設計高水位重現期50 a和2 a波浪作用下高樁碼頭的透射系數，詳見表2。該結果在前期數值波浪水槽基礎上做了驗證，整體上檢驗了數模的合理性，而物模試驗由于補充了更多工況條件、且結構模擬更精確，因此對于后續研究與方案設計依據將更加全面合理。

試驗中，由于防波堤兼顧碼頭的結構形式為直立式高樁透浪結構，波浪正向沖擊前沿擋浪板，形成直立反射，并形成較大上水。試驗工況情況下的越浪量如圖4所示，在極端高水位與設計高水位下發生較多整體越浪，越浪量較大，在設計低水位時主要為濺浪。

4-a 極端高水位4-b 設計低水位

5-a 水平力合力過程線5-b 下部浮托力合力過程線

在極端高水位、設計高水位和設計低水位情況下，分別組合重現期為100 a、50 a與15 a一遇的波浪作用，測定防波堤擋浪板所受到的波浪水平力、浮托力及其分布，并在此基礎上優化和改進斷面結構布置方案。 圖5為重現期100 a波浪作用下的擋浪板水平力過程線和下部浮托力過程線。

2.2.2 三維局部整體波浪物模

三維局部整體波浪物模僅針對防波堤開展建模，模型幾何比尺為30。試驗波要素提取自平面二維波浪試驗結果，并驗證了堤外的傳播分布規律，模型中采用單向不規則波，譜型為JONSWAP譜，譜峰因子取3.3。防波堤結構取自經過二維波浪斷面物理模型試驗優化后的斷面結構，以在之前研究基礎上進一步驗證調整后方案在不同浪向下的透浪系數以及堤后碼頭泊穩條件。分別模擬SSE、S、SSW，SW和WSW共五種波向，試驗中觀測到了波浪透射、反射與繞射并存的復雜傳播以及與堤頂越浪上水的現象，不同波向作用下的物模試驗場景如圖6-a～6-e所示。

6-a SSE向重現期50 a波浪作用6-b S向重現期50 a波浪作用

圖7 不同擋浪板入水深度時的碼頭損失作業天數和堤頂越浪量關系

另外，還選取代表波向作用下透空式堤外側擋浪板不同入水深度時透浪效果的對比試驗，試驗結果如圖6-f所示，這為進一步優化設計方案提供依據。同時，在物模試驗中可以更加直觀地看到高水位時除了透浪外，還有一部分波浪在堤前擋板出現反射以及越浪現象，且防波堤的透射系數隨著水位不同效果也有明顯的差異，表現為設計低水位時透浪率要大于設計高水位時，這與之前二維波浪水槽試驗結果相一致。此外，對比防波堤不同擋浪板入水深度的波高結果，隨著入水深度增加，碼頭波高逐漸減小，從而堤后碼頭的損失作業天數也隨著深度的增加而減少，有利于泊穩條件的改善。但是，其所帶來的不利影響即是堤外側的反射面增大，導致堤頂越浪量增加，其變化規律如圖7所示。

對比相同工況下試驗結果，物模與數模整體上比較接近，但在來浪方向與碼頭走向夾角較大時，物模試驗中堤后波高結果比數模偏小一些，除了反映出物模中完全對防波堤結構的復演體現了其消浪效果更顯著之外，實際水體受結構間的阻尼作用比數模反映的更為明顯，數值模擬的參數設置還有待于和原型間的驗證，綜合分析后物理模型試驗的結果將更接近真實情況[13]。

3 結語

復合建模方法集中了多種試驗技術手段的優點, 體現了多種試驗技術融合的發展方向。本文依托采用透空式防波堤的碼頭工程，結合平面二維波浪數學模型、二維數值水槽以及二維波浪物模水槽試驗和局部三維整體物模試驗的復合模型，對該防波堤的設計波浪要素、透浪特性、防波堤波浪荷載以及泊穩條件和越浪情況進行了研究分析，為工程設計的最終確定提供了科學依據。這種結合數值模擬和試驗室物模的復合建模雖然不是解決工程問題的最優方法，也不是解決問題的唯一途徑，但是復合建模在工程實際問題的研究中是一種很有前途的方法，可以充分利用有限的資源來從不同角度解決更復雜的實際問題。展望未來，港口航道與海岸工程的水工模型試驗在今后的發展將著眼于進一步提高成本效益、提高精度、減少模型間不確定性，也對研究團隊的多學科交叉提出了更高要求，包括數值模擬、物理模型和現場觀測等常規方法之間的交互應該得到重視和改進，以獲取更高質量的結果，如今單一的方法已難以支撐整個復雜工程，而復合建模正是綜合了各方面的優勢，今后應得到進一步重視，合理的設計與使用值得繼續深入研究與實踐。