系桿拱橋吊桿張拉方案優化試驗研究

王莉

（中鐵第一勘察設計研究院集團有限公司，陜西西安 710043）

系桿拱橋外部為靜定結構，內部為高次超靜定結構［1］，吊桿內力的改變對全橋受力狀態均有一定影響。系桿拱橋最常用的是柔性吊桿，其應力-應變曲線呈非線性，在長期荷載作用下會產生應力松弛和應力損失［2］。因此，系桿拱橋索力優化具有重要的實際意義。

朱敏等［3］通過零位移法和能量最小法的優化組合形成最優化的成橋狀態，建立了施工期結構狀態變量與成橋狀態目標之間的關系，從而得到不同施工階段合理的吊桿張拉力。任偉新等［4］指出將吊桿理想化為張緊的弦時，忽略了吊桿的垂度和抗彎剛度，在實際應用中會帶來不可接受的誤差。因此對弦公式進行了修正，采用能量法和曲線擬合法，建立了分別考慮索垂度和抗彎剛度影響、由基頻計算索力的實用公式。張戎令等［5-6］從吊桿受力分析出發，結合抗彎剛度，在考慮轉動慣量、剪切變形的影響和鋼絞線及高密度聚乙烯（High Density Polyethylene，HDPE）2 種復合材料耦合振動的情況下，推導出吊桿鉸接下索力計算公式。宋一凡等［7］引用斜拉索的動力計算長度概念得到吊桿的動力計算長度，然后將兩端固結支承的拉索振動問題等效成兩端鉸結支承的拉索振動問題，從而解決了長期以來用振動法測估索力時遇到的有效吊桿長度取值難題。既有研究成果完善了索體系理論，為實際工程索結構張拉提供了借鑒。

本文以蘭新二線新疆烏魯木齊河特大橋為1 跨128 m 系桿拱橋為背景，建立室內1/16 縮尺模型，研究不同初張拉力時張拉過程中索力變化規律及拆除支架后系梁的應力和線形，可為同類橋梁的吊桿張拉方案提供借鑒和參考。

1 模型試驗

1.1 模型設計

該橋為雙線鐵路橋，拱軸線為二次拋物線，矢跨比為1/5，系梁為單箱雙室，每道拱肋上有17 組吊桿，每組2 根，采用先梁后拱的施工方法。對系桿拱橋進行縮尺模型吊桿索力試驗，其幾何縮尺比例為1/16，依據相似原理確定模型橋與原型橋面積、剛度、質量等參數的相似系數，并進行截面設計。系梁尺寸見圖1，拱肋為啞鈴形截面（拱肋壁厚82 mm，拱肋外經1.4 mm），模型橋吊桿采用6×19φ6.2 mm的鋼絲繩，鋼絲繩采用U形鎖扣［5］將其錨固。

圖1 系梁尺寸（單位：cm）

為控制各吊桿索力，在模型橋拱肋安裝吊桿的位置安裝S 形拉式傳感器，在系梁底錨具上方安裝壓式傳感器，通過連接DH3016 靜態應變儀測試吊桿張拉過程中索力變化情況［8］。

吊桿上端與S 形傳感器連接，吊桿下端穿過系梁并錨固于齒板上，最后取拉式傳感器與壓式傳感器的平均值為該吊桿索力。在系梁L/8，L/4，3L/8，L/2，5L/8，3L/4，7L/8 截面布置百分表測試張拉過程中系梁撓度［9］。在系梁底緣拱腳和L/4，L/2，3L/4 截面布置應力應變計測試張拉過程中系梁應變。

模型橋測試試驗見圖2。

圖2 模型橋測試試驗

1.2 試驗工況

為便于研究，將每道拱肋上的吊桿按小里程到大里程依次編號，每道拱肋上每組吊桿分為A，B 吊桿，見圖3。

圖3 吊桿編號

在系梁L/4，L/2，3L/4 跨底布置臨時支墩，承擔系梁、拱肋全部重量。張拉時，橫向和縱向對稱的4根吊桿同時張拉，根據吊桿數量和實際工程中千斤頂張拉吊桿情況，試驗共分為10 個工況，每個工況共有8 根吊桿（工況3 除外）。如工況1，張拉吊桿號為5B13A，其左線和右線各有1 根吊桿，即2 根5B 和13A，共計4根吊桿同時張拉；然后張拉2 根5A 和13B；工況3 中，9A和9B為跨中吊桿，共有4根吊桿，一次張拉完畢。

系桿拱橋采用先梁后拱的形式，吊桿張拉方案的選取參考實際同跨徑的3座橋梁張拉力進行吊桿張拉試驗。依據相似比例將3 座橋的初始張拉力進行換算，對應的方案分別為方案1、方案3、方案4；將方案1對應橋梁的初始張拉力按加權平均值換算后作為方案2。

擬通過不同張拉力下吊桿內力重分布、系梁內力分布、成橋線形等進行分析。4 種張拉方案吊桿初始張拉力見表1。

表1 4種張拉方案吊桿初始張拉力 kN

2 試驗結果分析

2.1 吊桿索力變化

4種張拉方案索力變化見圖4。可知，系桿拱橋在分批張拉過程中，大多數吊桿表現出的規律是后批次張拉的吊桿索力對先批次張拉吊桿索力有明顯的卸載作用。如首批張拉的5#，13#吊桿，自張拉開始，在其他吊桿分批次張拉過程中，該吊桿索力一直呈減小趨勢，且張拉順序越靠后吊桿受到的影響越小。在系梁拆除支架后發生了體系轉換，由于系梁自重全部通過吊桿傳遞給鋼管混凝土拱肋，因此各吊桿索力均有所增加。但在不同批次張拉過程中1#，3#，9#吊桿索力變化呈加載、卸載循環狀態，表明少數吊桿在張拉過程中存在非線性應力重分布。

4 種方案下吊桿總張拉力分別為41.8，40.8，56.78，131.74 kN，方案1 和方案2 吊桿總張拉力相對較小，方案4吊桿總初張拉力最大，且其在不同工況吊桿張拉索力變化幅度較大。對比4 種方案下5#，1#，9#吊桿的索力變化情況，對于最先張拉的5#吊桿在方案1 中工況9 時索力減少為0，其余3 種張拉方案從張拉開始到張拉結束時索力分別減少了88.0%，78.9%和71.9%，方案3 和方案4 索力損失相對較少。1#吊桿為短吊桿，方案4吊桿初始張拉力最大，其值為3.45 kN，方案1 與方案2 吊桿張拉力相對較小，分別為1.37，1.20 kN。4 種張拉方案在體系轉換前的張拉過程中索力變化較均勻，卸載也較小。對于中間9#吊桿，在張拉過程中吊桿處于加載、卸載的循環狀態，從工況5到工況10 索力分別減少了63.7%，65.0%，58.6%和43.7%，方案3和方案4索力減少得相對較少。

圖4 4種張拉方案索力變化

綜合考慮吊桿初始張拉力、張拉過程中索力變化可知：方案4吊桿初始張拉力最大，張拉過程中吊桿索力相對較大且分布不均勻，該方案是不合理的；方案1與方案2中5#吊桿索力張拉完后卸載較大，也不合理；方案3比較合理。

2.2 恒載作用下系梁應力

恒載作用下系梁下緣應力見圖5。可知，4種方案各控制截面最大應力為2.4 MPa，均滿足規范要求。在跨中4 種方案截面下緣均受拉；在拱腳方案4 系梁下緣受拉，其余3 種方案系梁下緣受壓。 方案1 和方案2各控制截面應力比較接近且系梁下緣拉壓狀況相同，方案3 和方案4 各控制截面應力絕對值小于方案1和方案2。說明方案3和方案4優于方案1和方案2。

圖5 恒載作用下系梁下緣應力

2.3 拆除支架后系梁線形

吊桿張拉后拆除支架后系梁變形見圖6。可知，系梁變形整體上呈拋物線形，系梁撓度隨吊桿初始張拉力增大而減小。在跨中系梁變形最大，方案1 中撓度最大值為2.93 mm，是方案2 的1.03 倍，是方案3 的1.2 倍，是方案 4 的 3.7 倍。方案 1 與方案 2 在跨中附近撓度差別較小，其他位置系梁變形基本相等。方案4 在L/8 和7L/8 處發生了上拱，而在跨中附近下撓，這不利于系梁澆筑時預拱度的設置。相比之下，方案3優于其他3種方案。

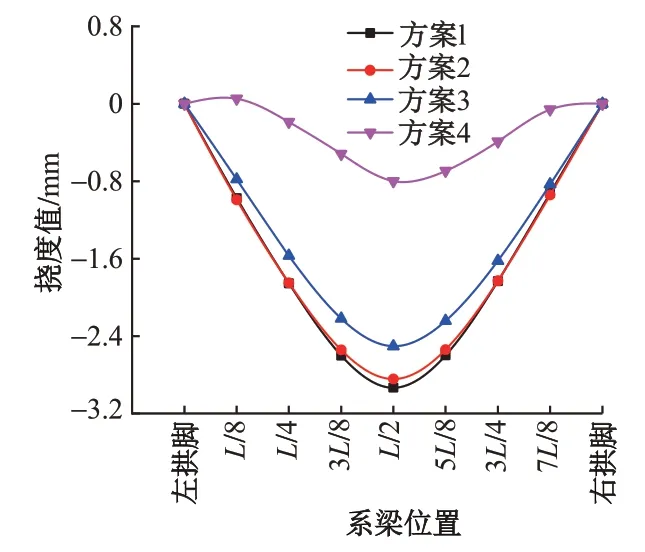
圖6 吊桿張拉后拆除支架后系梁變形

3 結論

本文以1 跨128 m 特大橋為工程背景，按照實際結構的計算參數，在室內1/16 縮尺模型上進行了同一張拉順序下不同吊桿索力試驗，得出以下結論：

1）4 種張拉方案中，方案4 初始張拉力最大，吊桿索力卸載較大；方案1中先張拉吊桿索力被完全卸載，有一定的不合理性；方案1 與方案2 吊桿索力變化趨勢基本一致；方案3 中各吊桿初始張拉力比原橋設計值偏大，但吊桿索力和系梁應力均滿足規范要求。考慮吊桿受力及系梁應力和變形，方案3較為合理。

2）吊桿在張拉過程中表現出明顯的應力重分布，后張拉的吊桿索力對先張拉的吊桿索力部分卸載，也會出現部分吊桿索力增大的現象，且應力重分布規律呈非線性變化。試驗中最先張拉的5#，13#吊桿索力受到的影響最大。

3）拆除支架后系梁變形呈拋物線形，吊桿索力、系梁撓度和系梁應力均增大。