補(bǔ)脾益氣散聯(lián)合西藥治療小兒秋季腹瀉療效觀察
李娜 張小明(陜西省黃陵縣人民醫(yī)院,陜西黃陵727300)
補(bǔ)脾益氣散聯(lián)合西藥治療小兒秋季腹瀉療效觀察
李娜 張小明
(陜西省黃陵縣人民醫(yī)院,陜西黃陵727300)
目的觀察補(bǔ)脾益氣散聯(lián)合西醫(yī)藥物治療小兒秋季腹瀉臨床效果及安全性。方法小兒秋季腹瀉患兒共150例,采用隨機(jī)數(shù)字表法分為對(duì)照組和中醫(yī)組,各75例;對(duì)照組給予西醫(yī)常規(guī)藥物治療,中醫(yī)組患者則在此基礎(chǔ)上加用補(bǔ)脾益氣散輔助治療。比較兩組患兒臨床療效,癥狀體征緩解時(shí)間,治療前后腹瀉頻率及不良反應(yīng)發(fā)生率等。結(jié)果中醫(yī)組患兒臨床療效顯著優(yōu)于對(duì)照組,差異有統(tǒng)計(jì)學(xué)意義(P<0.05);中醫(yī)組患兒癥狀體征緩解時(shí)間顯著短于對(duì)照組(P<0.05);中醫(yī)組患兒治療后腹瀉頻率均顯著低于對(duì)照組(P<0.05);同時(shí)兩組不良反應(yīng)發(fā)生率比較差異無(wú)統(tǒng)計(jì)學(xué)意義(P>0.05)。結(jié)論補(bǔ)脾益氣散聯(lián)合西醫(yī)藥物治療小兒秋季腹瀉可有效改善腹瀉癥狀體征及頻率,縮短臨床病程,且未增加不良反應(yīng)發(fā)生率。
小兒秋季腹瀉中醫(yī)藥安全性
小兒秋季腹瀉是一類主要由輪狀病毒感染所致的兒科消化道常見(jiàn)疾病,流行病學(xué)研究顯示,其好發(fā)于6個(gè)月至3歲嬰幼兒[1]。小兒秋季腹瀉患兒主要臨床表現(xiàn)為大便次數(shù)及性狀改變,常伴有嘔吐、發(fā)熱及脫水等,如不及時(shí)治療可造成嚴(yán)重水電解質(zhì)及酸堿平衡紊亂,威及生命[2-4]。目前西醫(yī)治療小兒秋季腹瀉尚無(wú)特效方案,常規(guī)對(duì)癥藥物干預(yù)近遠(yuǎn)期療效欠佳,無(wú)法滿足臨床需要。如何有效改善小兒秋季腹瀉患兒癥狀體征,加快病情康復(fù)進(jìn)程已越來(lái)越受到兒科學(xué)界的關(guān)注。本次研究以我院兒科近年來(lái)收治小兒秋季腹瀉患兒共150例作為研究對(duì)象,分別給予西醫(yī)常規(guī)藥物和在此基礎(chǔ)上加用補(bǔ)脾益氣散輔助治療;比較兩組患兒臨床療效,癥狀體征緩解時(shí)間,治療前后腹瀉頻率及不良反應(yīng)發(fā)生率等,觀察中西醫(yī)結(jié)合治療小兒秋季腹瀉臨床效果及安全性。現(xiàn)報(bào)告如下。
1資料與方法
1.1納入標(biāo)準(zhǔn)符合《中國(guó)腹瀉病診斷治療方案》(1998年)急性水樣腹瀉診斷及分型標(biāo)準(zhǔn)[4];符合中醫(yī)泄瀉脾虛濕盛證辨證診斷標(biāo)準(zhǔn)[5];年齡≤24個(gè)月;輪狀病毒(+);研究方案經(jīng)醫(yī)院倫理委員會(huì)批準(zhǔn);患兒家長(zhǎng)簽署知情同意書,自愿加入研究。排除標(biāo)準(zhǔn):入組前未行抗生素及止瀉藥物應(yīng)用;重度脫水;嚴(yán)重心腦肝腎功能障礙;藥物過(guò)敏;治療依從性差;臨床資料不全,失訪及脫落。
1.2臨床資料研究對(duì)象選取我院兒科2014年9月至2015年5月收治小兒秋季腹瀉患兒共150例,采用隨機(jī)數(shù)字表法分為對(duì)照組和中醫(yī)組,各75例。對(duì)照組男性35例,女性40例;年齡10~24個(gè)月,平均(12.82± 2.30)個(gè)月;病程2~5 d,平均(3.14±1.10)d。中醫(yī)組男性37例,女性38例;年齡12~24個(gè)月,平均(12.90± 2.35)個(gè)月;病程3~5 d,平均(3.20±1.16)d。兩組患兒臨床資料差異無(wú)統(tǒng)計(jì)學(xué)意義(P>0.05)。
1.3治療方法對(duì)照組給予西醫(yī)常規(guī)藥物治療,包括抗病毒、退熱、腸黏膜保護(hù)劑、合理喂養(yǎng)、糾正水/電解質(zhì)平衡紊亂及益生菌(培菲康,1歲以內(nèi)每日0.5 g,1歲及以上每日1.0g溫水沖服)等;中醫(yī)組患兒則在此基礎(chǔ)上加用補(bǔ)脾益氣散輔助治療,方藥為人參15 g,茯苓15 g,白術(shù)10 g,山藥10 g,薏苡仁10 g,陳皮10 g,蓮子肉6 g,桔梗6 g,砂仁6 g;食積甚者加山楂6 g,腹痛甚者加肉桂6 g(此劑量主要針對(duì)24個(gè)月小兒);每劑加水500mL煎至100mL,早晚溫服,其內(nèi)可加適量紅糖;兩組患者治療時(shí)間均為3 d。
1.4觀察指標(biāo)記錄患兒癥狀體征緩解時(shí)間,包括脫水(口渴癥狀消失,啼哭時(shí)伴眼淚流出,且尿量及次數(shù)恢復(fù)正常)、腹瀉(大便次數(shù)<3次/d)及發(fā)熱(腋下體溫<37.4℃)等;分別于治療前、治療后24 h和24 h記錄患兒總腹瀉次數(shù),計(jì)算每天腹瀉發(fā)作頻率;記錄患兒不良反應(yīng)發(fā)生例數(shù),計(jì)算發(fā)生率;不良反應(yīng)類型主要包括皮疹和便秘。
1.5療效標(biāo)準(zhǔn)[6]顯效:患兒治療3 d內(nèi)腹瀉頻率及大便性狀恢復(fù)正常,全身癥狀體征基本消失。有效:患兒治療3 d內(nèi)腹瀉頻率、大便性狀及全身癥狀體征明顯緩解。無(wú)效:患兒治療3 d內(nèi)腹瀉頻率、大便性狀及全身癥狀體征未見(jiàn)緩解或加重。
1.6統(tǒng)計(jì)學(xué)處理本次研究數(shù)據(jù)、錄入及邏輯糾錯(cuò)選擇Epidata 3.10軟件,數(shù)據(jù)分析選擇SPSS13.0軟件;其中計(jì)量資料以(±s)表示,采用t檢驗(yàn);計(jì)數(shù)資料采用χ2檢驗(yàn),以百分比(%)表示;檢驗(yàn)水準(zhǔn)為α=0.05。P《 0.05為差異有統(tǒng)計(jì)學(xué)意義。
2結(jié)果
2.1兩組患兒臨床療效比較見(jiàn)表1。中醫(yī)組患兒臨床療效顯著優(yōu)于對(duì)照組(P《0.05)。

表1 兩組患兒臨床療效比較(n)
2.2兩組患兒癥狀體征緩解時(shí)間比較見(jiàn)表2。中醫(yī)組患兒癥狀體征緩解時(shí)間均顯著短于對(duì)照組,差異有統(tǒng)計(jì)學(xué)意義(P《0.05)。

表2 兩組患兒癥狀體征緩解時(shí)間比較(h?
2.3兩組患兒治療前后腹瀉頻率比較見(jiàn)表3。中醫(yī)組患兒治療后腹瀉頻率顯著低于對(duì)照組、治療前,差異有統(tǒng)計(jì)學(xué)意義(P《0.05);
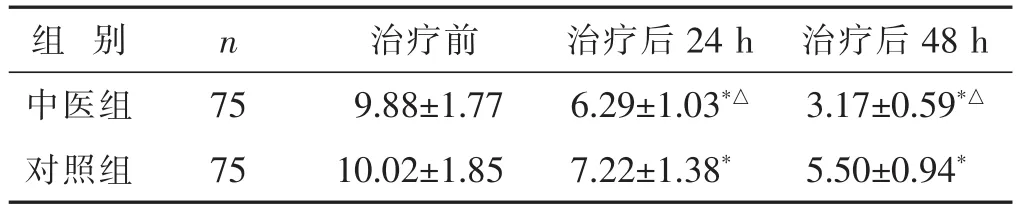
表3 兩組患兒治療前后腹瀉頻率比較(次/d,?
3 討論
已有研究顯示,小兒秋季腹瀉發(fā)生與患兒機(jī)體免疫系統(tǒng)及消化系統(tǒng)發(fā)育尚未成熟關(guān)系密切;對(duì)于尚無(wú)自我進(jìn)食能力患兒不合理喂養(yǎng)、氣溫驟變及病原菌侵襲是導(dǎo)致發(fā)病主要原因[7-9]。目前西醫(yī)治療小兒秋季腹瀉一般在常規(guī)補(bǔ)液、抗感染及保護(hù)腸黏膜等基礎(chǔ)上加用腸道益生菌以調(diào)節(jié)腸道內(nèi)環(huán)境。
中醫(yī)學(xué)將小兒秋季腹瀉歸于“泄瀉”范疇,病機(jī)為脾胃弱致乳哺失調(diào),風(fēng)寒濕邪干正所致;而運(yùn)化失常、水谷合污而下,終引泄瀉而生[10-13]。補(bǔ)脾益氣散組分中人參補(bǔ)中益氣,茯苓健脾燥濕,白術(shù)滲濕益氣,山藥補(bǔ)氣益脾,薏苡仁祛濕健脾,陳皮消積理氣,蓮子肉止瀉健脾,桔梗利水行氣,砂仁化濕合胃,食積甚者加山楂健胃消滯,腹痛甚者加暖陽(yáng)止痛;諸藥合用可共奏益氣滲濕,健脾祛濕之功效,且溫燥適宜,藥效平和。現(xiàn)代藥理學(xué)研究證實(shí),人參、茯苓及白術(shù)提取物均可發(fā)揮增強(qiáng)機(jī)體免疫功能,抑制病毒繁殖等作用,這亦是本方劑扶正祛邪之關(guān)鍵所在[14-15]。服用時(shí)加入紅糖可起合胃健脾之效,同時(shí)亦可改善口感,提高患兒治療依從性。
本研究結(jié)果顯示,中醫(yī)組患兒臨床療效和癥狀體征緩解時(shí)間均顯著優(yōu)于對(duì)照組,差異有統(tǒng)計(jì)學(xué)意義,提示中西醫(yī)結(jié)合治療小兒秋季腹瀉有助于緩解臨床癥狀體征,加快病情康復(fù)進(jìn)程;中醫(yī)組患兒治療后腹瀉頻率顯著低于對(duì)照組,差異有統(tǒng)計(jì)學(xué)意義,提示中醫(yī)藥輔助用于小兒秋季腹瀉治療在控制腹瀉頻率,提高生活質(zhì)量方面優(yōu)勢(shì)明顯;而兩組患兒不良反應(yīng)發(fā)生率比較差異無(wú)統(tǒng)計(jì)學(xué)意義,則說(shuō)明消補(bǔ)脾益氣散聯(lián)合西醫(yī)藥物治療小兒秋季腹瀉安全性符合臨床應(yīng)用需要。
綜上所述,補(bǔ)脾益氣散聯(lián)合西醫(yī)藥物治療小兒秋季腹瀉可有效改善腹瀉癥狀體征及頻率,縮短臨床病程,且未增加不良反應(yīng)率。
[1]McFarland LV.Antibiotic-associated diarrhea:epidemiology,trendsand treatmen[J].Future Microbiol,2008,30(3):563-578.
[2]羅菲.熱毒寧聯(lián)合蒙脫石散對(duì)輪狀病毒腹瀉患兒止瀉效果分析[J].實(shí)用藥物與臨床,2013,16(7):644-645.
[3]唐敬麗.消旋卡多曲顆粒在嬰幼兒輪狀病毒性腸炎治療中的臨床應(yīng)用[J].中國(guó)醫(yī)療前沿,2012,7(12):48.
[4]方鶴松,魏承毓.中國(guó)腹瀉病診斷治療方案[J].中國(guó)實(shí)用兒科雜志,1998,13(6):381-384.
[5]中華人民共和國(guó)衛(wèi)生部.中藥新藥臨床研究指導(dǎo)原則[M].北京:中國(guó)醫(yī)藥科技出版社,2002:152.
[6]全國(guó)腹瀉病防治學(xué)術(shù)探討會(huì).腹瀉病療效判斷標(biāo)準(zhǔn)的補(bǔ)充建議[J].中國(guó)實(shí)用兒科雜志,1998,13(6):384.
[7]梁建中,郭思,李軼,等.消旋卡多曲顆粒聯(lián)合小兒氨基酸治療嬰幼兒輪狀病毒性腸炎[J].中國(guó)實(shí)用醫(yī)刊,2012,39 (19):48-50.
[8]王麗媛,謝詠梅,汪志凌,等.益生菌調(diào)節(jié)輪狀病毒腸炎患兒腸道菌群的動(dòng)態(tài)變化[J].實(shí)用兒科臨床雜志,2011,26 (7):489-461.
[9]楊生泉.參苓白術(shù)散加減結(jié)合利巴韋林治療小兒秋季腹瀉52例[J].陜西中醫(yī),2013,34(11):1461-1462.
[10]程健國(guó).熱毒寧注射液聯(lián)合培菲康治療小兒秋季腹瀉臨床療效觀察[J].湖南中醫(yī)藥大學(xué)學(xué)報(bào),2012,32(2):25-27.
[11]裴文利.秋瀉靈合劑與潘生丁聯(lián)合治療小兒秋季腹瀉的臨床療效觀察[J].2014,32(10):2528-2530.
[12]韓新民,汪受傳,虞舜,等.小兒泄瀉中醫(yī)診療指南[J].中醫(yī)兒科雜志,2008,4(3):1-3.
[13]沈亞婷.針?biāo)幉⒂弥委熜浩⑻撔篂a舉隅[J].醫(yī)藥衛(wèi)生(全文版),2016,2(3):286.
[14]黃向紅,林國(guó)榮,郭子寬.秋瀉方治療小兒秋季腹瀉臨床觀察[J].遼寧中醫(yī)藥大學(xué)學(xué)報(bào),2013,15(3):201-202.
[15]劉勇,陳娟.參苓白術(shù)散治療小兒秋季腹瀉45例[J].中國(guó)實(shí)驗(yàn)方劑學(xué)雜志,2011,17(1):181-182.
R725.7文獻(xiàn)標(biāo)志碼:B
1004-745X(2016)07-1441-02
10.3969/j.issn.1004-745X.2016.07.062
2015-10-17)

