大模數重載齒條中的缺陷應力場數值模擬

閆曉青，鄭衛力，張銀婷，黃曉歡

(長江三峽通航管理局，湖北 宜昌 443002)

三峽升船機是目前世界上提升質量最大的全平衡垂直升船機，驅動機構采用齒輪齒條爬升式，齒輪齒條為重要受力構件。驅動機構最大事故載荷8 800 kN。根據《機械設計手冊》，當齒輪齒條載荷較大時,應對齒輪和齒條材料、硬度和熱處理工藝進行專項研究。現行方法是通過解析解與有限元法計算相結合進行校核，再通過模型試驗對齒輪齒條接觸應力進行論證以確定合理制造工藝。在齒輪齒條制造過程中難免存在夾雜物及其他缺陷，但設計過程并未考慮缺陷工況，很多文獻研究成果表明，受力構件的損傷和失效的演化都是從夾雜物與金屬基體的交界部位開始[1]。因此，本文采用Ansys Workbench建立了含有夾雜物及蝕坑的齒輪齒條接觸三維有限元模型，計算各工況下齒條接觸應力及剪應力，并分析了不同缺陷工況下齒條力學性能，對齒條內夾雜物含量控制、齒輪齒條運行維保提供了科學的理論依據。

1 有限元模型建立

1.1 齒輪齒條技術參數

三峽升船機齒輪齒條是驅動機構的承載元件，正常工作狀態下，驅動機構小齒輪與齒條保持嚙合，驅動機構載荷通過齒條傳遞給混凝土結構。小齒輪軸兩側的軸段支承在支承與導向機構的軸承座內，齒輪齒條結構如圖1所示，齒輪齒條主要技術參數見表1。

表1 齒輪齒條主要技術參數

圖1 齒輪齒條嚙合示意(單位：mm)

1.2 有限元模型建立

根據齒條中夾雜物尺寸、形狀、分布特點，為了在有限元軟件中模擬夾雜物對齒條應力的影響，基于文獻[2-3]對齒條內夾雜物及缺陷描述“夾雜物存在于齒條部分單元中，且夾雜物彈性模量為鋼材的0.30～0.75倍，泊松比為0.178～0.306”，因此，本文做如下假設：1)齒條內夾雜物沿齒輪齒條嚙合作用線分布，夾雜物設置見圖2。2)由于夾雜物存在，且夾雜物與鋼基體彈性模量、泊松比不同，通過改變夾雜物的材料常數來模擬夾雜物對齒條接觸應力及剪應力的影響。3)對存在夾雜物單元進行更為細小剖分，剖分越接近夾雜物真實尺寸，計算結果越真實有效。夾雜物的尺寸為0.5 mm×0.5 mm×1 mm的立方體。為了在有限元軟件中便于施加齒輪的彎矩，齒輪中心設置直徑100 mm的圓孔，本文主要研究齒條的應力，齒輪中心開孔對計算結果影響較小可忽略[4-7]。齒輪齒條嚙合為線接觸，并且隨時間推移接觸線呈規律變化，為了精確模擬齒輪齒條的相對運動及運動過程產生的應力應變，對兩者進行動態接觸模擬分析，采用Ansys Workbench中的瞬態分析功能，齒輪齒條三維有限元模型見圖3。

圖2 齒條內夾雜物分布(單位：mm)

圖3 齒輪齒條嚙合有限元模型

2 計算結果及分析

2.1 設計的理想工況

齒條設計過程在確定加工及熱處理工藝時，未考慮缺陷的工況，為設計的理想工況。根據三峽升船機設計文件，升船機正常運行驅動機構最大工作載荷為1 100 kN，小齒輪等效載荷為932 kN。將升船機在超載工作狀態下的小齒輪載荷分為4個工況，工況1：驅動機構載荷超過1 560 kN時，監測和控制系統發出報警，小齒輪等效載荷為1 322 kN；工況2：驅動機構載荷超過1 580 kN時，主拖動系統開始電氣制動，至船廂停止升降后，工作制動器和安全制動器先后上閘，小齒輪等效載荷為1 339 kN；工況3：驅動機構載荷達到1 650 kN時，液氣彈簧開始動作，小齒輪等效載荷為1 398 kN；工況4：當安全機構螺紋間隙消失時，驅動機構最大事故荷載2 200 kN，此時小齒輪等效載荷為1 864 kN。

2.1.1理論計算

根據《機械設計手冊》[8]，齒輪齒條接觸應力為：

(1)

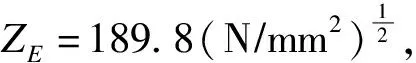
其中螺旋線載荷分布系數KHβ為：

(2)

通過計算得到4種工況下齒輪齒條的接觸應力為651.1、655.3、669.6、773.2 MPa。升船機正常運行最大載荷狀態下，齒輪齒條接觸應力為545.7 MPa。

2.1.2有限元分析計算

齒輪和齒條嚙合是復雜的接觸問題，且理論計算結果與與齒輪齒條運行的接觸應力存在一定誤差，因此對上述4種工況進行復核。齒輪材料為18CrNiMo7-6 ME，熱處理后踏面硬度為56～61HRC，齒條材料為G35CrNiMo6-6+QT1，熱處理后踏面硬度≥520 HV。將4種工況下小齒輪受力轉換成扭矩為1 122.7、1 137.1、1 187.5、1 583.3 kN·m。

Ansys Workbench在做接觸分析的非線性問題時，若選取整個模型分析，需要較多的單元、節點和內存空間，同時花費大量的求解時間，計算精度也會受到影響。為方便分析，僅建立模型的12進行計算，沿齒輪齒條中心對稱XY平面簡化模型，設置邊界條件時，在對稱面上添加“symmetric”約束[9-11]。齒輪齒條基體取彈性模量E=206 GPa，泊松比ν=0.3，齒輪與齒條的面的嚙合接觸設置為有摩擦約束，摩擦系數為0.3。瞬態分析時給齒輪內孔設置扭矩。計算結果見表2和圖4、5。

表2 不同工況下齒條最大接觸應力計算結果

圖4 不同算法對齒條最大接觸應力影響

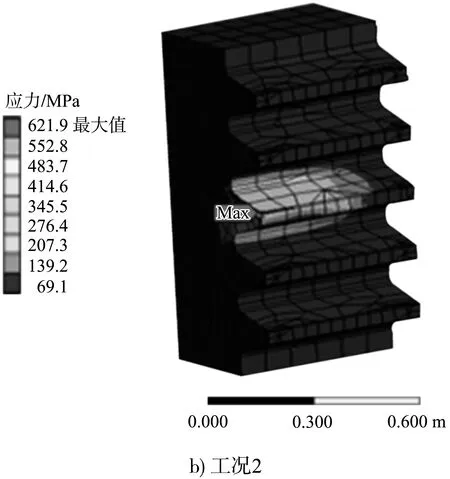
圖5 不同工況下齒條接觸應力云圖

由表2、圖4、5可知：1)4種不同載荷工況下齒輪齒條嚙合最大接觸應力均發生在嚙合表面。2)查看圖5中工況4齒條最大應力為852.9 MPa，位置并未在嚙合處，而是出現在了齒條齒頂內部的單元耦合部位，查看計算結果判定為應力集中點。忽略應力集中點，齒條的最大應力為嚙合表面的758.1 MPa。3)不同工況下隨著載荷增大，接觸應力呈非線性增大趨勢。4)有限元計算結果與理論計算的偏差均小于5%，在合理偏差范圍之內。

2.2 齒條含夾雜物

2.2.1不同載荷工況下

含夾雜物齒條分析計算時，夾雜物取彈性模量E=300 GPa，泊松比ν=0.2，齒輪與齒條的嚙合面、齒頂部缺陷與齒輪面的接觸設置為“有摩擦約束”，摩擦系數設置為0.3；其余夾雜物與齒條的接觸設置為“固定約束”。夾雜物位置網格劃分見圖6，計算結果見表3、圖7。

圖6 齒條夾雜物位置網格劃分

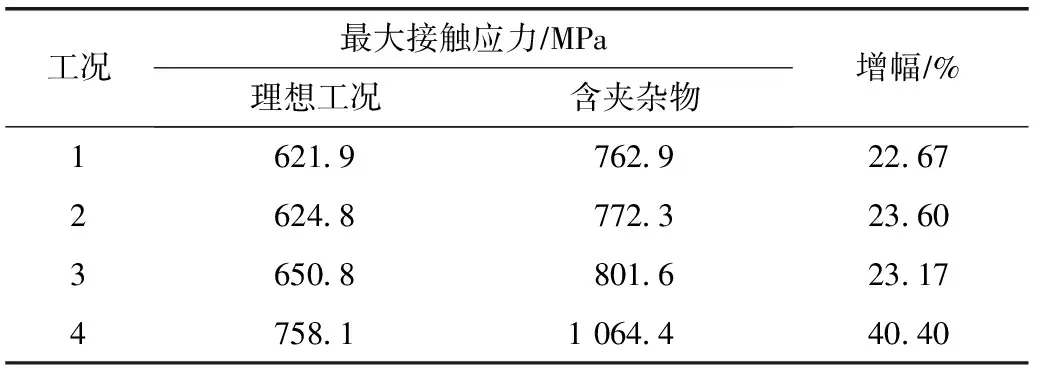
表3 含夾雜物不同工況下齒條最大接觸應力

圖7 含夾雜物不同工況下齒條接觸應力云圖

由表3、圖7可知：1)齒條含有夾雜物時，嚙合作用線位置夾雜物出現較大的應力。2)齒條在設計理想工況和含夾雜物工況下，隨著荷載增加，齒輪齒條接觸應力均呈非線性增大，在最大事故工況荷載作用下接觸應力增幅劇烈，因此，在重載工況下齒條內夾雜物對齒條影響較大。3)在事故工況下，齒條雖不會被破壞，但可能出現不可恢復的形變，齒輪齒條長期運行，在交變應力作用下會發生膠合和齒面接觸疲勞，出現安全事故。

2.2.2不同彈性模量工況

齒輪齒條基體彈性模量取E1=206 GPa，用遠小于齒條基體彈性模量E2=1 GPa模擬齒條中氣孔，對齒條中夾雜物彈性模量再分別取E2=150、206、300、412、620 GPa進行模擬，在最大事故工況4,計算1 864 kN等效荷載作用下齒條的最大接觸應力及最大剪應力，結果見表4、圖8。

表4 不同彈性模量夾雜物下齒條的最大接觸應力和最大剪應力

圖8 不同彈性模量夾雜物對齒條應力影響

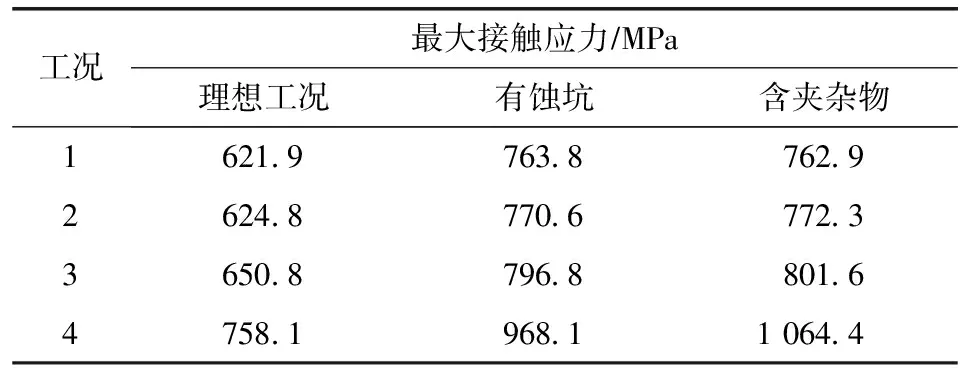
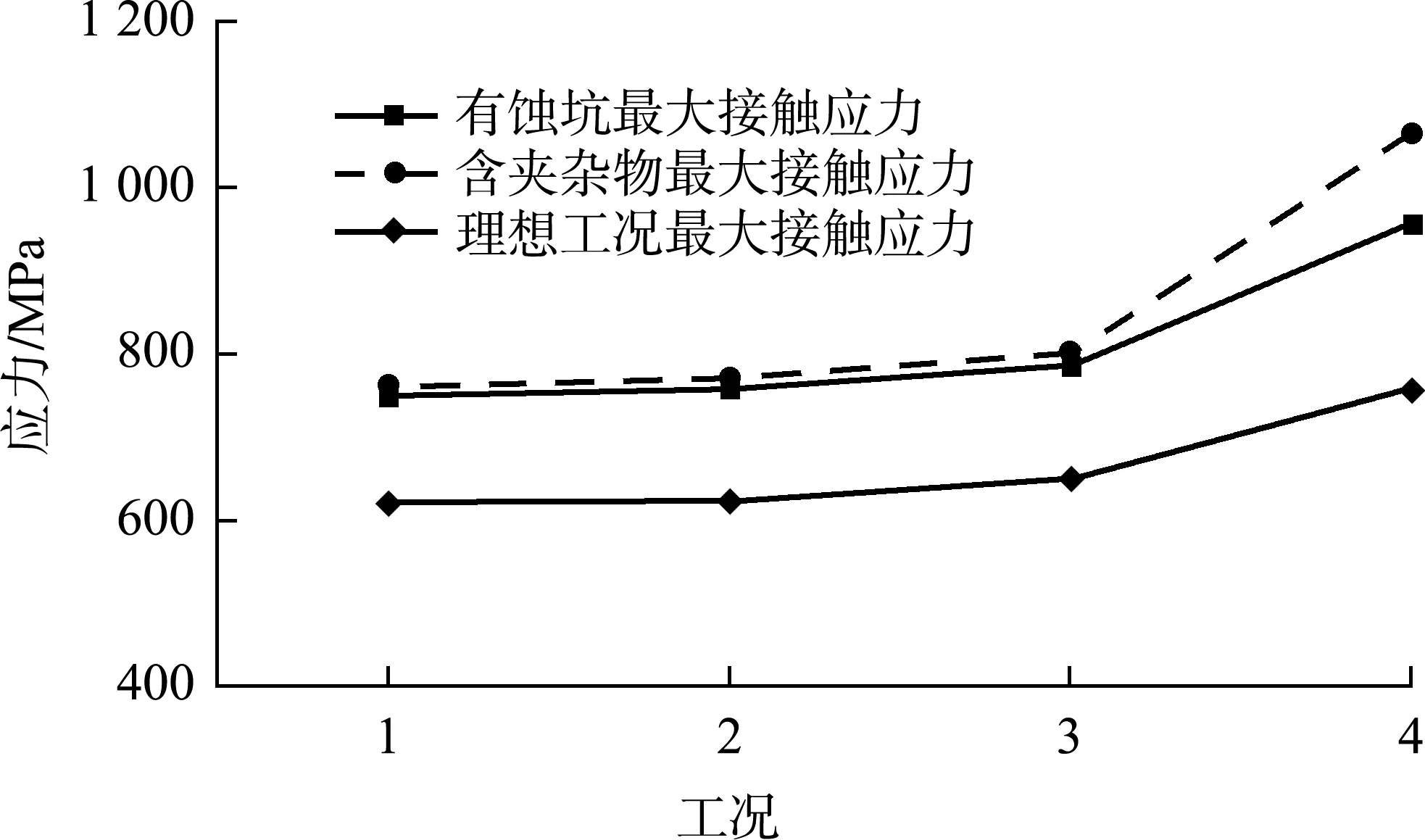
由圖8、表4可知：1)當彈性模量E2>E1、E2=E1、E2

2.2.3不同泊松比工況

對齒條內夾雜物泊松比分別取ν2=0.04、0.06、0.09、0.20、0.30，齒條基體泊松比取ν1=0.3，同樣在最大事故工況4,計算1 864 kN等效荷載作用下的齒輪齒條的最大接觸應力及最大剪應力，結果見表5、圖9。

表5 不同泊松比夾雜物齒條的最大接觸應力和最大剪應力

圖9 不同泊松比夾雜物對齒條應力影響

由圖9、表5可知：1)當泊松比ν2<ν1時，齒條的最大接觸應力與最大剪應力隨著泊松比的增大而減小，成反比例關系，最大接觸應力與最大剪應力均發生在夾雜物齒條基體交界位置附近。2)當泊松比ν2=ν1(即不含夾雜物)時，齒條最大接觸應力與最大剪應力發生在b1點，即齒輪齒條嚙合作用線上。3)有夾雜物區域齒條最大接觸應力和最大剪應力均大于ν2=ν1時的最大接觸應力與最大剪應力，而不在嚙合作用線上的c1、c2、c3點夾雜物的應力相對較小，表明齒輪齒條嚙合作用線上的夾雜物對齒條應力影響較大，而非嚙合線的夾雜物對齒條應力影響較小。

2.3 嚙合表面有蝕坑

在設計的理想工況模型的基礎上，建立蝕坑的缺陷模型，缺陷為0.5 mm×0.5 mm×1 mm的立方體，沿嚙合方向和齒厚方向的分布，與夾雜物分布相同。模型分析時，齒輪與齒條的嚙合面的接觸設置為“有摩擦約束”，摩擦系數設置為0.3。計算結果見表6和圖11、12。

表6 齒面蝕坑不同工況下齒條的最大接觸應力

圖10 齒面蝕坑不同工況下齒條接觸應力云圖

圖11 齒面蝕坑對齒條最大接觸應力的影響

由表6和圖10、11可知：1)齒條表面有蝕坑時，嚙合作用線位置蝕坑出現較大的應力。2)齒面有蝕坑工況下，隨著荷載增加，齒條接觸應力均呈非線性增大，在最大事故工況荷載作用下接觸應力增幅劇烈，因此，在重載工況下齒條蝕坑對齒條應力影響較大。3)在齒條表面有蝕坑時，比設計理想工況時應力增大22.8%、23.3%、22.4%和27.7%，與齒條含有夾雜物相比，在重載條件下，夾雜物比蝕坑更容易引起齒條的應力集中。

3 結論

1)采用Ansys Workbench有限元分析軟件模擬計算了齒條在含夾雜物、蝕坑等缺陷應力場分布情況，在齒條內缺陷數量和分布特點未知情況下，假設一種夾雜物及蝕坑的數目及分布策略，可有效分析缺陷對齒條受力的影響，夾雜物和蝕坑使得齒輪齒條嚙合過程最大接觸應力及最大剪應力位置發生變化。

2)該方法對齒條熱處理過程控制齒面及齒頂淬硬層達到硬化深度、減少夾雜物對齒條的影響及齒輪齒條維護保養等提供理論依據。