多機械臂系統無模型自適應神經網絡同步控制

(中國石油大學(華東)化學工程學院，山東 青島 266580)

隨著工業4.0和中國制造2025戰略的提出，生產制造業朝著數字化、智能化快速發展。而機械臂在制造業中有著重要的地位，多種操作任務都需要機械臂通過相互協作才能完成[1-3]。人們往往無法獲取機械臂所有精確的動力學參數，難以為其建立準確的數學模型[4-5]。并且機械臂在操作過程中還存在各種干擾等不確定因素，這就使其數學模型更加偏離實際系統。因此，機械臂同步控制的關鍵就在于其精確系統模型的建立以及對外界干擾的估計和補償，其中還需考慮各子系統之間的耦合關系[6]。

由于神經網絡對非線性系統具有極好的學習能力，因此對于機械臂這種多輸入多輸出的復雜非線性系統，神經網絡控制方法已經有一定的研究和應用。Cansever[7]針對三連桿機械臂設計了一種基于徑向基函數(radical basis fanction，RBF)神經網絡的模糊滑模控制器，其中RBF徑向基函數(radical basis fanction，RBF)神經網絡用于計算系統動力學所要求的等效控制ueq，模糊邏輯則用于調整滑模控制器增益。顧義坤等[8]基于自回歸神經網絡和自適應動態面方法設計了針對柔性關節機械臂的控制器，使得柔性關節的軌跡跟蹤精度顯著提高。Tang等[9]針對機械臂系統的強非線性和參數不確定性問題提出了一種基于RBF神經網絡的自適應PID控制器，其中PID控制器參數和雅克比矩陣采用神經網絡進行調節和在線識別[9]。董君等[10]針對機械臂軌跡運動誤差的問題，將神經網絡與非線性積分滑模相結合設計了控制器，提高了定位精度，并與傳統控制方法進行了對比。乃永強等[11]采用極限學習機對單隱層前饋神經網絡的隱層節點和權重系數選擇進行優化，提高了學習速度，對剛性機械臂系統不確定性進行逼近，保證了閉環系統的穩定性。Kumar等[12]基于RBF神經網絡對結構不確定性進行離線訓練，設計了一種針對冗余機械臂的自適應軌跡跟蹤控制器，并利用自適應控制器對非結構不確定性和網絡建模誤差的邊界進行了估計。

雖然目前神經網絡在機械臂控制中已經取得了一定成果，但大多只用于對系統不確定項或外界干擾的估計。而在系統極為復雜難以建模或全部參數都未知的情況下，尚無較好的控制方法。本研究首先對機械臂任務空間動力學模型進行簡單分析，運用RBF神經網絡對模型重力、哥氏力等分別獨立進行建模和在線學習，并基于圖論原理定義了各機械臂之間的耦合關系，根據滑模控制方法設計出一種新的無模型自適應神經網絡同步控制算法。所設計的同步控制器不僅具有較強的魯棒性，而且不依賴受控系統的數學模型。

圖1 多機械臂系統模型Fig. 1 Multiple robotic manipulators system model

1 機械臂動力學方程

假設由n個m關節串聯機械臂在同一任務空間完成操作任務，其系統模型如圖1所示。

取被控對象為多機械臂系統，根據Euler- Lagrange定理可知，在關節空間內其動力學方程為：

(1)

由于大多數操作任務都與機械臂末端執行器的空間位置相關，需要直接在任務空間中設計控制算法，因此需將機械臂系統動力學模型由關節空間轉換到任務空間中。假定任務空間有界，Jacobian矩陣是非奇異的，可以通過轉換函數和Jacobian矩陣將關節空間坐標轉換到笛卡爾坐標空間中[5]：

(2)

則機械臂系統任務空間中的動力學模型為：

(3)

2 機械臂神經網絡建模

2.1 RBF神經網絡

RBF神經網絡是一種結構簡單、訓練高效的前饋式神經網絡，被廣泛應用于模式識別和非線性函數逼近等領域[13-15]。

圖2 RBF神經網絡結構圖Fig. 2 RBF neural network structure

RBF神經網絡算法可以表示為：

(4)

2.2 RBF神經網絡建模

考慮其中任意一個機械臂子系統，采用RBF神經網絡對其動力學各部分分別進行建模。由于機械臂轉動慣量矩陣Mix(q)和重力矩陣Gix(q)僅是q的函數，因此采用靜態神經網絡建模如下[16]：

其中：mxkj、gxk分別為Mix(q)、Gix(q)中的元素，k、j分別表示矩陣的行和列，l表示神經網絡節點；θkjl、βkl∈R分別為mxkj(q)和gxk(q)的神經網絡權重；ξkjl(q)、ηkl(q)∈R為相應的徑向基函數，其輸入均為q；εmkj(q)、εgk(q)∈R為建模誤差，假設其有界。

根據神經網絡模型，第i個機械臂在任務空間中的動力學方程可以寫為：

(5)

其中：

(6)

其中，{Θi}、{Αi}、{Ξi(q)}和{Ζi(z)}為GL矩陣，其元素分別為θkj、αkj、ξkj(q)和ζkj，{Βi}和{Ηi(q)}為GL向量，其元素分別為βk和ηk(q)，矩陣EMi(q)、ECi(z)∈Rm×m和EGi(q)∈Rm的元素分別為建模誤差εmkj(q)、εckj(z)和εgk(q)。

3 同步控制器設計

對機械臂之間的同步誤差進行定義，基于滑模控制方法設計了神經網絡自適應同步控制器。

3.1 同步誤差和交叉耦合誤差

機械臂的跟蹤誤差可以定義為：

e=xd-x。

(7)

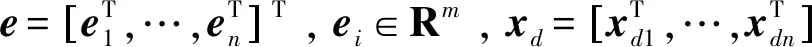
根據圖論思想，每個機械臂之間的耦合關系可以由拉普拉斯矩陣進行定義：

L=D-A。

(8)

則機械臂系統的同步誤差可以寫成如下形式：

(9)

機械臂子系統之間的交叉耦合誤差定義為：

(10)

3.2 神經網絡滑模同步控制器

定義如下形式：

(11)

滑模函數定義為如下形式：

(12)

則：

(13)

其中，Λ=ΛT>0。

將式(6)、(11)代入機械臂動力學方程(3)中可得：

(14)

設計神經網絡同步控制器如下：

(15)

將式(11)、(15)代入式(14)可得：

(16)

設計神經網絡自適應律為：

(17)

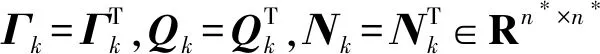
定理1針對式(5)所示的機械臂系統，若滑模面設計如式(12)，神經網絡自適應律為式(17)，在同步控制律(15)的控制作用下，每個機械臂都可以從任意初始位置追蹤期望軌跡，且同步誤差最終可以漸進收斂至零。

證明：選取如下Lyapunov函數：

(18)

求導可得：

(19)

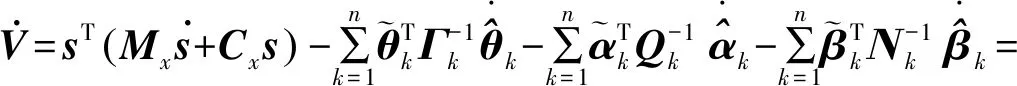
(20)

(21)

即當t→∞時，s→0。

當s=0時，可得：

選取Lyapunov函數如下：

(22)

則：

(23)

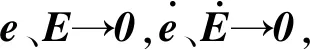
3 機械臂同步控制Matlab仿真

3.1 機械臂及控制器參數

以兩個平面二連桿機械臂為例，設計機械臂任務空間同步控制Matlab仿真。假設每個機械臂初始位置和速度不同，但具有相同的結構和動力學參數，動力學方程如下：

其中：

其中，pl為負載，P為機械臂參數向量，l1、l2為兩連桿的長度。

由于給定的期望軌跡一般直接在任務空間中表示，因此需要將關節角位置坐標轉換為連桿末端的笛卡爾坐標：

機械臂Jacobian矩陣為：

則

機械臂實際有關參數如下：

在笛卡爾坐標空間中期望軌跡設置為：

表1 控制器參數設置Tab. 1 Controller parameter setting

兩個二連桿機械臂在任務空間中的初始狀態參數為：

同步控制器參數設置見表1，拉普拉斯矩陣設置為：

神經網絡初值設為0，其他參數設置如下：

3.2 仿真結果及分析

基于上述參數的仿真結果如圖3～9所示。

多機械臂系統任務空間的軌跡和速度跟蹤仿真結果如圖3～5，可以看出，兩機械臂從任務空間中的不同位置出發，在神經網絡同步控制器(15)的作用下，大約0.8 s左右時可以同時到達預定的期望軌跡；0.4 s左右時，兩機械臂可以達到期望的運動速度。在到達期望軌跡后，兩機械臂均沿期望繼續保持同步運動，且不再發生較大波動。在第4 s時使兩機械臂的載荷增加，在增加的瞬間，機械臂會略微偏離預定軌跡，但在神經網絡同步控制器(15)的作用下可以迅速向期望軌跡收斂。機械臂系統在任務空間中的仿真結果如圖4，可以看出，在到達預定軌跡前，兩機械臂首先實現了同步運動。

圖3 機械臂x、y方向軌跡跟蹤曲線Fig. 3 Trajectories tracking of robotic manipulators in x and y direction

通過仿真結果圖6可以看出，兩機械臂關節的輸出力矩雖在初始時刻有較大波動，但隨后即穩定在|τ|≤40 N·m范圍內。在第4 s載荷增加后，力矩則維持在|τ|≤90 N·m的范圍內進行波動。機械臂神經網絡建模仿真結果如圖7，圖中分別表示了機械臂動力學方程Mx、Cx和Gx項的神經網絡建模結果。 可以看出，機械臂動力學模型可以通過神經網絡進行逼近，但未收斂到理想值，存在一定的建模誤差，造成這種不收斂現象的原因主要有兩種：一是指令信息未能達到持續激勵條件，即不足夠豐富而造成；二是除真實值外，還存在多個估計值滿足軌跡跟蹤收斂條件。但此誤差可以通過滑模魯棒項進行抵消。

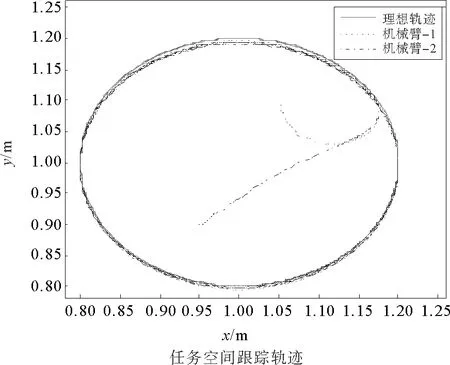
圖4 任務空間中機械臂軌跡跟蹤曲線Fig. 4 Trajectories tracking of robotic manipulators in task space

通過仿真結果圖8和圖9可知，在系統受擾動后兩機械臂跟蹤誤差最終可以向0漸進收斂，兩機械臂同步誤差也可以在控制器作用下快速地收斂到0。即在同步控制器(15)的控制作用下，雖然在第4 s時載荷發生變化，兩機械臂依然可以實現同步運動并滿足操作精度要求。

綜合分析仿真結果3～9，可以得到以下結論：利用所提出的神經網絡自適應同步控制算法，在機械臂系統結構參數未知和存在外界干擾的情況下，即使各子系統均具有較大的初始誤差，也可以使機械臂末端位置在控制器的作用下快速收斂至期望軌跡，并實現同步運動。

圖5 機械臂x、y方向速度跟蹤曲線Fig. 5 Velocity tracking of robotic manipulators in x and y direction

圖6 兩連桿機械臂關節驅動力矩Fig. 6 The joint driving torque of two connecting rod manipulators

圖7 機械臂動力學模型逼近Fig. 7 Manipulator dynamics model approximation

圖8 兩機械臂x、y方向跟蹤誤差Fig. 8 Tracking error of the two robotic manipulators in x and y direction

圖9 兩機械臂x、y方向同步誤差Fig. 9 Synchronization error of the two robotic manipulators in x and y direction

4 結論

針對結構復雜難以建立準確數學模型或系統參數未知、多變的復雜多機械臂系統的任務空間同步控制問題進行了研究，設計出一種新的任務空間神經網絡自適應同步控制算法。主要結論如下：

1) 對多機械臂系統進行動力學分析，利用RBF神經網絡對系統不同動力學結構分別進行網絡建模，對實際模型進行實時逼近，擺脫了數學模型的限制；

2) 考慮了各機械臂之間的耦合關系，并根據圖論思想定義了各子系統之間的交叉耦合誤差，在此基礎上設計的同步控制器可以保證系統在載荷發生改變等不確定情況下依然能夠實現同步；

3) 結合滑模控制原理，提出了一種任務空間中的機械臂無模型神經網絡自適應同步控制算法，在初始誤差較大的情況下也可以保證對期望軌跡實現快速跟蹤，提高了控制器的魯棒性。