例談晶胞計算
2020-02-29 03:41:04閆翠紅
高中數理化 2020年3期
閆翠紅
由于晶體結構知識能全面考查學生的觀察能力、思維能力和空間想象能力,在分析這類題目時,可讓學生通過對晶體結構的觀察,利用分攤法來解決晶體中所含的微粒數、晶體的化學式等問題.
1 晶胞中粒子數目的計算——均攤法
原則:晶胞任意位置上的1個原子如果是被n個晶胞所共有,那么每個晶胞對這個原子分得的份額就是1/n.
1) 平行六面體晶胞中不同位置的粒子數,根據均攤法情況如圖1所示.
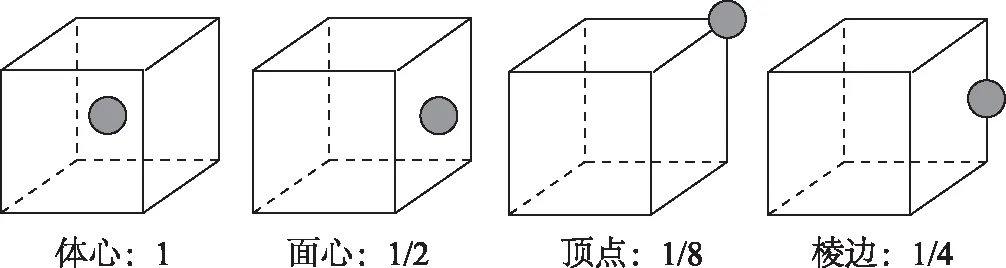
圖1
2) 六棱柱、三棱柱、平面晶體結構單元中頂點、棱上的微粒的均攤情況見表1.
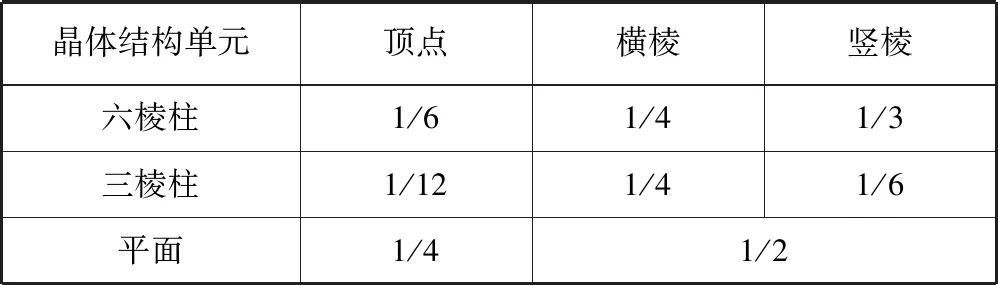
表1 各類晶體結構單元均攤情況

A. 8 B. 12 C. 24 D. 60
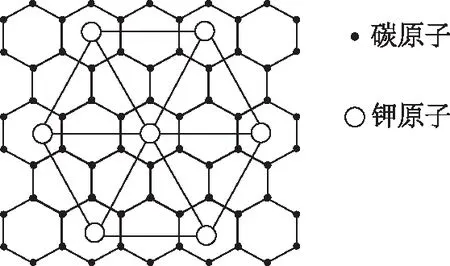
圖2

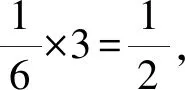

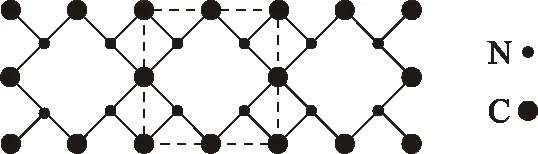
圖3
A. 氮化碳屬于原子晶體
B. 氮化碳中碳顯-4價,氮顯+3價
C. 氮化碳的化學式為C3N4
D. 每個碳原子與4個氮原子相連,每個氮原子與3個碳原子相連

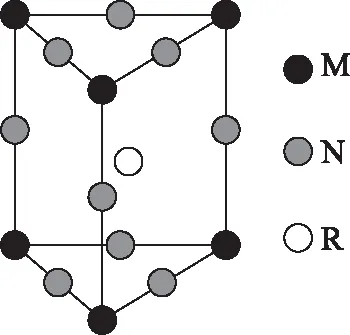
圖4

A. 1∶4∶2
B. 2∶9∶4
C. 3∶8∶4
D. 3∶9∶4

2 晶胞密度的相關計算
對于立方晶胞,可建立如下求算途徑:
1) 計算出1 個晶胞中粒子個數;
2) 推算出1 mol 晶胞中含粒子的物質的量;

表2 各類晶胞棱長與粒子半徑的關系
4) 密度的單位常用g·cm-3, 晶胞參數的單位需要與密度單位統一,經常用到的換算關系有:1nm=10-7cm=10-9m,1pm=10-10cm=10-12m.
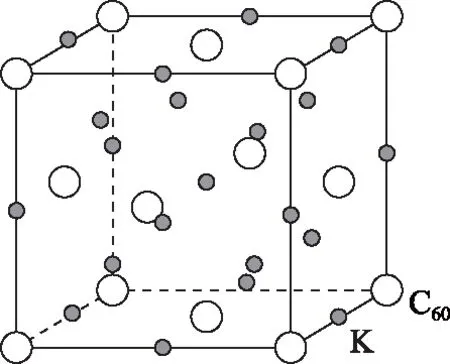
圖5


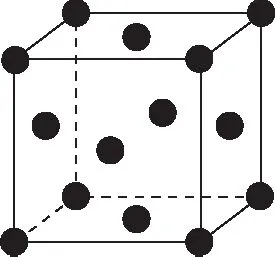
圖6


a3×9.00g·cm-3×NA=4×64g·cm-3,
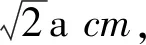

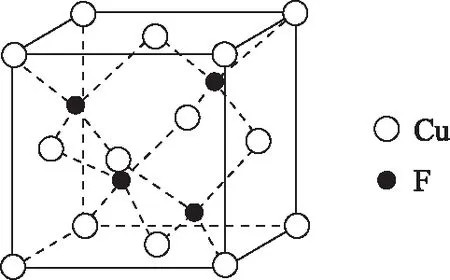
圖7

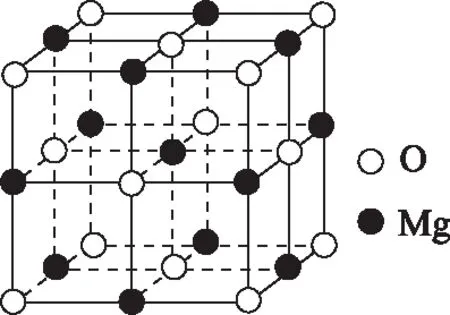
圖8



