基于改進準則法的復合殼阻尼結構拓撲減振動力學優化

袁維東，高瞻，劉浩康，繆國峰

航空工業南京機電液壓工程研究中心 航空機電系統綜合航空科技重點實驗室，南京 211106

減振作為現代機械發展中一項重要研究課題，如何有效地抑制結構無益振動是研究的首要內容，尤其是在航空航天、智能制造等高動力現代科技的領域，對結構的減振動力學性能提出了更高的要求。其中以“輕”“薄”為主要特性的殼板薄壁構件，在外部激勵下極易引起振動，因此勢必要對其振動進行控制[1]。對于結構振動的控制一般可分為：主動控制和被動控制。近些年來，在結構表面附加黏彈性阻尼材料的被動減振技術已成為一種實用、有效減振降噪措施。實踐表明，黏彈性阻尼材料具有高阻尼特性，在振動變形過程中通過相位的時滯特性來耗散能量，能在十分寬泛的頻帶內抑制結構的振動與噪聲，故常被用作振動結構的減振材料。自從Kerwin和Edward[2]提出以黏彈阻尼材料構建約束阻尼結構以來，其越來越廣泛應用于工程實踐。不過，對于具有高速和大動力化的減振對象，如航空航天中的多數結構，因其具有輕量化要求，采用在結構上全覆蓋阻尼材料的方案，并非是減振控制的最優布局構型。為此，如何有效地敷設黏彈性阻尼材料、提高結構減振效果成為研究阻尼結構拓撲減振的重點。

不少學者研究了殼阻尼結構的減振特性，進一步完善了阻尼結構減振理論和技術。Bieniek和Freudenthal[3]通過建立殼中性面的受迫振動，分析了約束阻尼結構振動；王目凱等[4]提出了在指定頻帶內能量耗散系數的評價標準，對約束阻尼殼結構進行參數分析。同時，對于薄壁構件在約束阻尼結構最優拓撲構型方面的減振優化，也開展了相關研究工作。Pedersen[5]采用了連續體結構的優化準則法，分析了求解拓撲優化域的局部模態與優化參數的數學邏輯關系；楊德慶和柳擁軍[6]提出阻尼胞單元和阻尼拓撲敏度概念，給出了靈敏度排序方式減振優化準則；Lima等[7]推導了復數形式的靈敏度公式，建立了約束阻尼板頻率和溫變響應的優化減振函數；郭中澤和陳裕澤[8]以模態損耗因子最大化為設計目標，采用變密度拓撲優化，實現了優化準則法求解最優分布構型。可以看出，結構拓撲減振優化的基礎理論在不斷地建立和推進，但較多的是以薄板的阻尼結構為首選對象給予了研究，而對薄殼減振優化的研究相對較少。Kumar和Singh[9-10]通過實驗對圓柱殼主動約束阻尼層位置進行優化。王明旭和陳國平[11]基于均勻化方法，研究了約束阻尼殼結構的拓撲減振效果，得出多模優化效果更佳的結論；柳承峰等[12]以漸進優化算法，研究了約束阻尼殼結構的布局優化，獲得較強的振動能量耗損；石慧榮等[13]選取前三階模態最大損耗因子為目標函數，利用多目標遺傳算法對兩端簡支的圓柱殼進行優化分析；Kim等[14]從模態振型、應變能密度和優化算法3方面，對約束阻尼殼結構減振拓撲構型的振動效果進行了數值仿真和實驗驗證，進而得出優化算法的拓撲減振優勢。對于黏彈性阻尼材料本構數學模型，Johnson和Kienholz[15]基于模態應變能法(Modal Strain Energy, MSE)，構建了將阻尼結構復數解簡化為實數解模態損耗因子的理論方法。

優化準則法(Optimality Criteria, OC)是拓撲優化變密度法中的一種迭代求解算法，具有完備的理論依據和工程應用價值。其應用于靜力學結構時，每一拓撲變量均能取得正數值，然而在動力學結構中則會有非全域迭代拓撲變量的負靈敏度，以至于全域優化變量并不能整體尋優。這種只有其中部分變量參與優化迭代的方式將導致拓撲變量值跳躍和不連續的狀況發生，最終迭代結果將不收斂或局部收斂[16-17]。為了滿足和提升結構的動力學性能，發揮OC法優勢，應用于以航空航天等領域薄殼結構為研究對象的拓撲減振動力學優化問題研究，本文基于變密度法的拓撲動力學優化理論，從數學的理論角度，建立了優化目標靈敏度一般公式，演算全局優化設計變量的改進準則法，并分析了薄殼復合結構的拓撲減振以及多模態減振優化問題。

1 阻尼結構拓撲減振模型

1.1 結構模態損耗因子

為了衡量復合殼約束阻尼結構的減振效果，根據結構振動基本理論，可采用結構模態損耗因子推進阻尼結構拓撲減振動力學優化。對于黏彈性阻尼減振材料，其材料損耗因子比一般彈性材料高幾個數量級，通常可忽略金屬材料損耗因子，并且在優化迭代中涉及大量的結構動力學參數和阻尼材料復數本構模型的計算，十分耗時，故本文基于能量的角度進行研究。根據有限單元法(Finite Element Method, FEM)和模態應變能法(MSE),可得復合殼阻尼結構的模態應變能計算式為

(1)

式中：Ei、μi分別為第i階模態應變能和振型；K為剛度矩陣。

黏彈性動力學理論表明，其有明顯的溫度和頻率非線性的變化特性，目前已建立了多種不同的力學本構模型，但較為實用的是常復數模量模型[18]，進而復合殼阻尼結構的模態損耗因子寫成

(2)

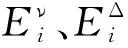
以便于諧響分析，對于復合殼阻尼結構采用黏彈性阻尼材料，基于模態應變能法[19]，其模態損耗因子與模態阻尼比之間數學關系：ηi≈2ξi。并可寫出阻尼結構的第i階模態振動平衡方程：

(3)

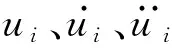
1.2 插值函數變密度模型

變密度法是基于某種插值模型，建立優化結構材料的物理屬性與偽密度之間的函數關系，通過優化設計變量的數值變化來決定優化結構材料的分布狀態。固體各向同性材料懲罰模型(Solid Isotropic Microstructures with Penalization，SIMP)的優化求解過程中，阻尼結構的約束材料與對應的阻尼材料存在狀態[0,1]作一致變化，可建立復合殼阻尼結構插值模型數學公式為

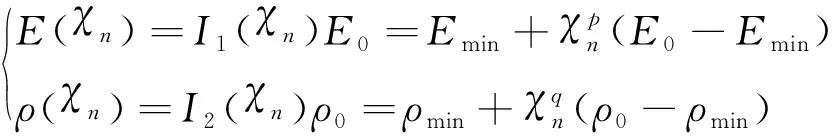
(4)

式中：E0、ρ0分別為阻尼材料的楊氏彈性模量和密度；n為有限元網格的單元數；χn為第n個單元插值模型的偽密度或設計變量；p、q為SIMP插值模型的懲罰因子；Emin、ρmin為了避免優化迭代中出現奇異值問題，通常設置為0.001；I1(χn)、I2(χn)為材料插值模型函數。

基于有限元法單元矩陣組合理論，可有

(5)

式中：下標s、v、c和上標e分別為約束阻尼結構的基層、阻尼層、約束層和有限單元標識；M為質量矩陣；TN為優化區域約束阻尼有限單元數。

1.3 結構動力學優化模型

任何實際問題均需要構建數學模型，以便于展開問題的定量分析。阻尼結構的拓撲減振優化也不例外，首先建立優化目標函數，明確指明優化求解的迭代方向。在約束阻尼結構中優化目標可以結構振動的固有特性參數，如固有頻率、模態損耗因子或模態阻尼比等作為目標，當然也可采用若干特征點的振幅或加速度、動撓度以及響應頻率等。鑒于模態損耗因子可以表征在某階振動時耗損能量多少的度量，其值越大，表示阻尼結構耗能越多，故可以以模態損耗因子為優化目標。然而考慮到優化準則法是以目標函數的極小值形式出現，為了便于借助現存的一些成熟優化迭代技巧推進優化，本文以模態損耗因子負值最小作為優化模型的目標函數。在此基礎上，增加移動常數，使目標函數為正值，以便于對目標函數進行數值分析。為滿足減振設計的結構輕量化要求，通常優化模型的約束條件之一是對在基體上使用黏彈性阻尼材料的體積作一定限制，與此同時減振優化對象尋優前后，不宜使結構的動態特性如頻率、模態、振型等出現過大的變化，影響預期結構優化性能[20-21]。綜上因素，復合殼阻尼結構的拓撲減振優化數學模型為

(6)

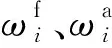
在工程實踐中，結構的工作頻率段振動通常包括前幾階振型，并且在不同激擾條件下，其振動貢獻會發生一定的改變。因此，在考慮多模態復合優化的同時，通過不同的權重系數?i來控制各階模態的減振效果，且最好依據模態參與因子取定?i。當然，也可對某一階頻率進行減振優化分析，選取權重系數為1，其他階次頻率權重系數為0，故可看出此拓撲優化目標函數具有較廣的適用性。

2 減振優化目標靈敏度分析

變密度法拓撲優化中，優化目標函數的尋優方向主要取決于對拓撲優化設計變量求解的梯度，即靈敏度，它準確反映了優化迭代方向的敏感性。加之目標函數是單模態優化線性疊加的數值關系，由此可先推演單模態減振優化靈敏度數值公式。

對式(2)求模態損耗因子梯度，并整理可有

(7)

(8)

根據結構動力學有限元理論，可知復合殼阻尼結構模態滿足：

(9)

將式(9)等號兩邊同時對χn求偏導，整理得

(10)

(11)

聯立式(9)和式(10)整理求解可有

(12)

接著，將式(10)～式(12)變換求解可得

(13)

為了使目標靈敏度具有廣泛的應用價值，基于材料插值模型函數，推導一般靈敏度計算公式。

將式(1)對設計變量求偏導，可有

(14)

聯立式(7)、式(8)、式(13)和式(14)，則整理推導出

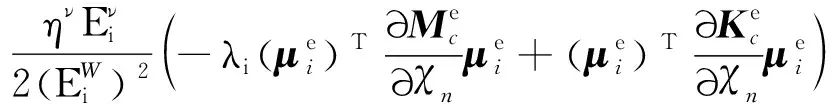
(15)

式(4)可作變換有

E′(χn)=I′1(χn)E0=

(16)

ρ′(χn)=I′2(χn)ρ0=

(17)

基于有限元的單元能量理論，可得

(18)

(19)

進一步將式(15)、式(18)和式(19)聯立可有

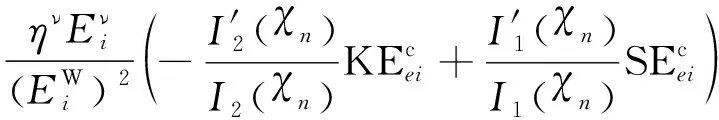
(20)

式中：KEei、SEei分別為當前某一迭代單元的第i階模態動能和模態應變能；I′1(χn)、I′2(χn)為材料插值模型一階導數。

3 拓撲減振優化算法

已有研究表明，基于優化準則法(OC)的設計變量啟發式迭代格更新方法，是一種與優化結構設計變量數量無關的迭代公式，具有優化尋優效率高和嚴格的理論推導等特點。不過，在動力學拓撲優化中靈敏度數值以實數范圍變化，即正數或負數均可出現。若直接采用靜力學中優化準則法進行動力學優化求解，勢必引起設計變量負值的出現，將會導致優化迭代無法進行。常規動力學優化準則法通過將正的靈敏度置為零，保留負靈敏度值，而這樣做易引起拓撲變量跳躍以及局部優化解[22]。因此，以復合殼阻尼結構為研究對象，基于改進準則法進行拓撲減振動力學演算。

3.1 動力學改進準則法

建立不隨優化目標凸性的求解算法，根據優化理論，基于數學規劃法中序列凸規劃方法構建相似性函數，并建立泰勒展開式逼近，推導優化數學模型嚴格凸性條件。首先對式(6)演算拉格朗日優化函數[23]：

(21)

式中：Λ、β-n、β+n均為拉格朗日乘子。僅須進一步滿足Karush-Kuhn-Tucke條件，并求其極值點處的χn值，即有

?ψ/?χn+Λ(?V/?χn)-β-n+β+n=0

(22)

為了構造相似性函數，引入移動參數c，令ψ-cV=ψ*，Λ=Λ*-c，并代入式(22)，得

(?ψ*/?χn)+Λ*(?V/?χn)-β-n+β+n=0

(23)

進一步令yn=(1/χn)ζ，根據泰勒展開思想構造逼近函數，即使自變量yn逼近ψ*，接著可令

(24)

式中：ψ0為一常數。推導式(24)對yn導數，則

?ψ*/?yn=αn

(25)

顯然，當αn≥0時，近似函數ψ*具有嚴格凸性。

另一方面推導式(24)對χn導數，可得

?ψ*/χn=?[αn(χn)-ζ]/?χn=

?(ψ-cV)/?χn

化簡并整理后，有

αn=-(?ψ/?χn-c(?V/?χn))(χn)ζ+1/ζ

(26)

c≥(?ψ/?χn)/(?V/?χn)

(27)

確定移動參數c數值關系，使αn≥0滿足函數嚴格凸性條件。

3.2 構建改進準則法迭代律

在建立凸性條件的基礎上，完成啟發式迭代格的推導。為此，對式(21)進一步細化設計變量的優化迭代空間，并簡化算式可令δn=?V/?χn，這樣便將式(21)函數整理簡化為

式中：

(28)

式中：Ω、-Ω、+Ω分別表示拓撲設計變量的中間值、最小值和最大值集合。為了求解式(28)，在求解式(29)所示數學問題同時，結合式(22)和式(23)求得，即

min:ln,χmin≤χn≤χmax

(29)

同理，由拉格朗日極值條件易得

(30)

將αn、δn代入式(30)化簡得設計變量滿足極值條件迭代格為

(31)

式中：k為迭代次數。若令Q=(?ψ/?χn)/(?V/?χn)，并結合式(27)可知，Q是一個與設計變量數量有關的參量，可建立第k次迭代中參數ck用∞-范數表示：ck=‖Q‖∞，且Q=[Q1,Q2,…,Qn]T。考慮到每次迭代時設計變量的移動極限，故改進準則法的設計變量迭代格為

(32)

并且，

式中：λ(0<λ<1)為設計變量移動極限值。

在優化算法尋優過程中，大量的偽密度設計變量更新帶來了優化對象的不同片區物理屬性躍變，避免優化前后振型發生紊亂致使優化拓撲構型失效。在迭代優化中通過振型控制因子(MAC)的數值大小[23]，直觀的反映每次迭代情況，其計算公式為

(33)

式中：τ≤1正系數，一般取值0.9。迭代格更新設計變量時，優化振型趨于穩定的量化MAC近于1。若有變化，則須調整迭代格參數，并作進一步迭代尋優。

復合殼阻尼結構減振尋優，借助大型商用軟件ANSYS給予數值處理，通過二次開發語言APDL編程實現改進準則法迭代格。圖1為算法程序流程圖。

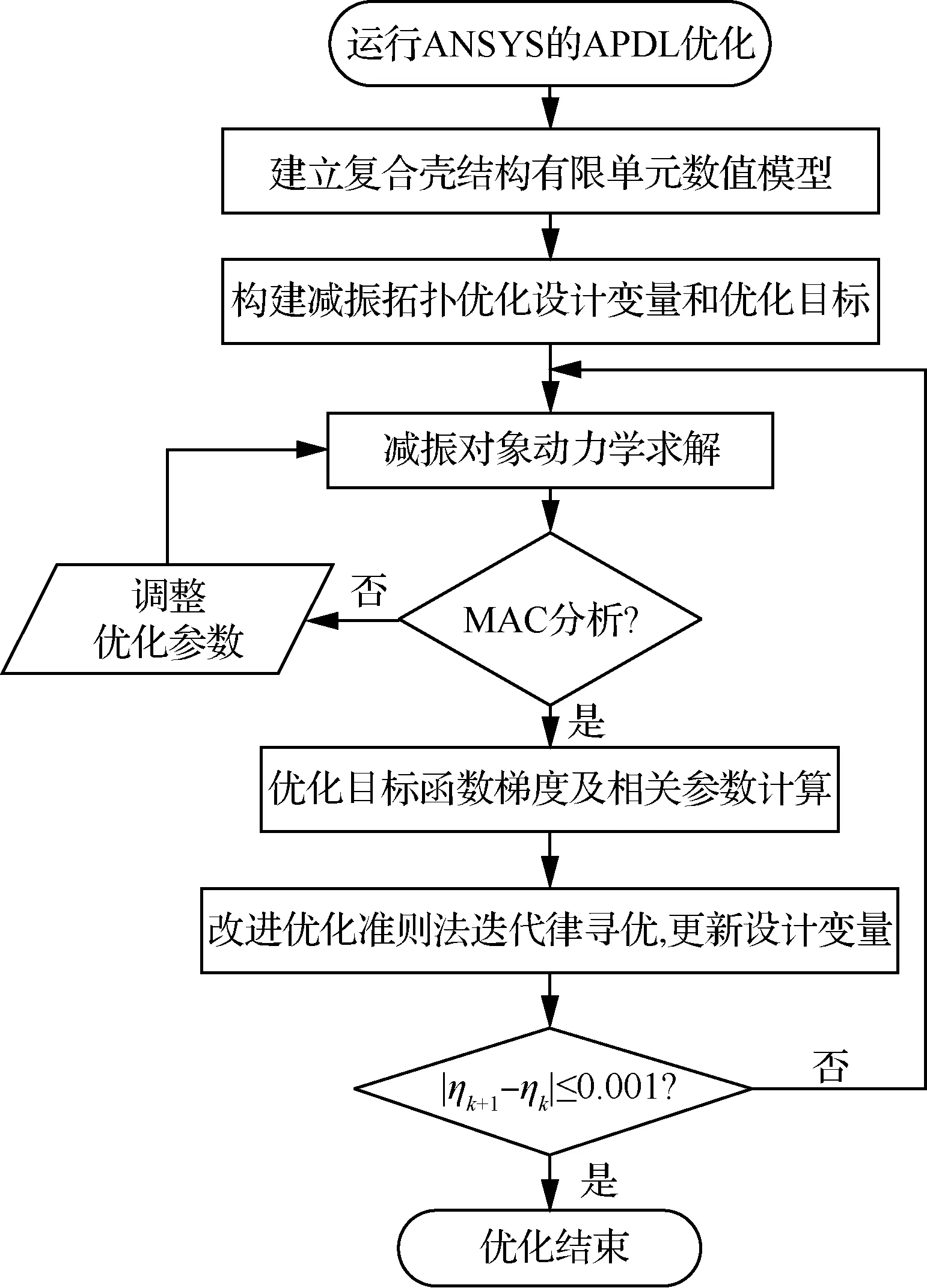
圖1 復合殼結構減振拓撲優化實現流程Fig.1 Topology optimization procedure for damping shells

4 優化算例分析

為了進一步分析和驗證上述減振拓撲優化的理論，采用航空航天等工程中應用廣泛的復合殼結構作為優化對象。

殼結構外形尺寸參數弧度半徑R=1 m，轉角θ=30°，長度L=0.55 m。基體材料厚度3 mm，楊氏彈性模量43.2 GPa，泊松比0.33，密度1 810 kg/m3。黏彈性阻尼材料楊氏彈性模量15 MPa，密度為1 550 kg/m3，泊松比0.495，材料損耗因子0.75，鋪設厚度1 mm。黏彈性阻尼材料應用于被動三層約束阻尼結構，約束層厚度1.5 mm，采用與基層相同的材料。同時作用于結構的諧響應激勵力為單位力，提取頻率1～200 Hz，圖2給出了薄殼一端固支約束、激勵點、提取點和前三階模態應變場。

對結構前三階模態振型，運用改進準則法進行拓撲減振優化，約束層與阻尼層視為一層優化結構，且優化后材料體積為全覆蓋的50%。表1為優化目標函數權重系數的5種不同取值情況，分別代表全覆蓋約束阻尼層、一階優化、二階優化、三階優化和前三階多模態減振優化數值計算的設定值，并列出了相應的結構損耗因子和固有頻率的數值結果。其中，主要考慮前三階模態減振中的權系數加權作用，以求結構損耗因子最大值的優化目標，因此權重系數?1=?2=?3=1/3。以下拓撲減振分析中，未指明的情況下均為改進準則法的尋優數據。

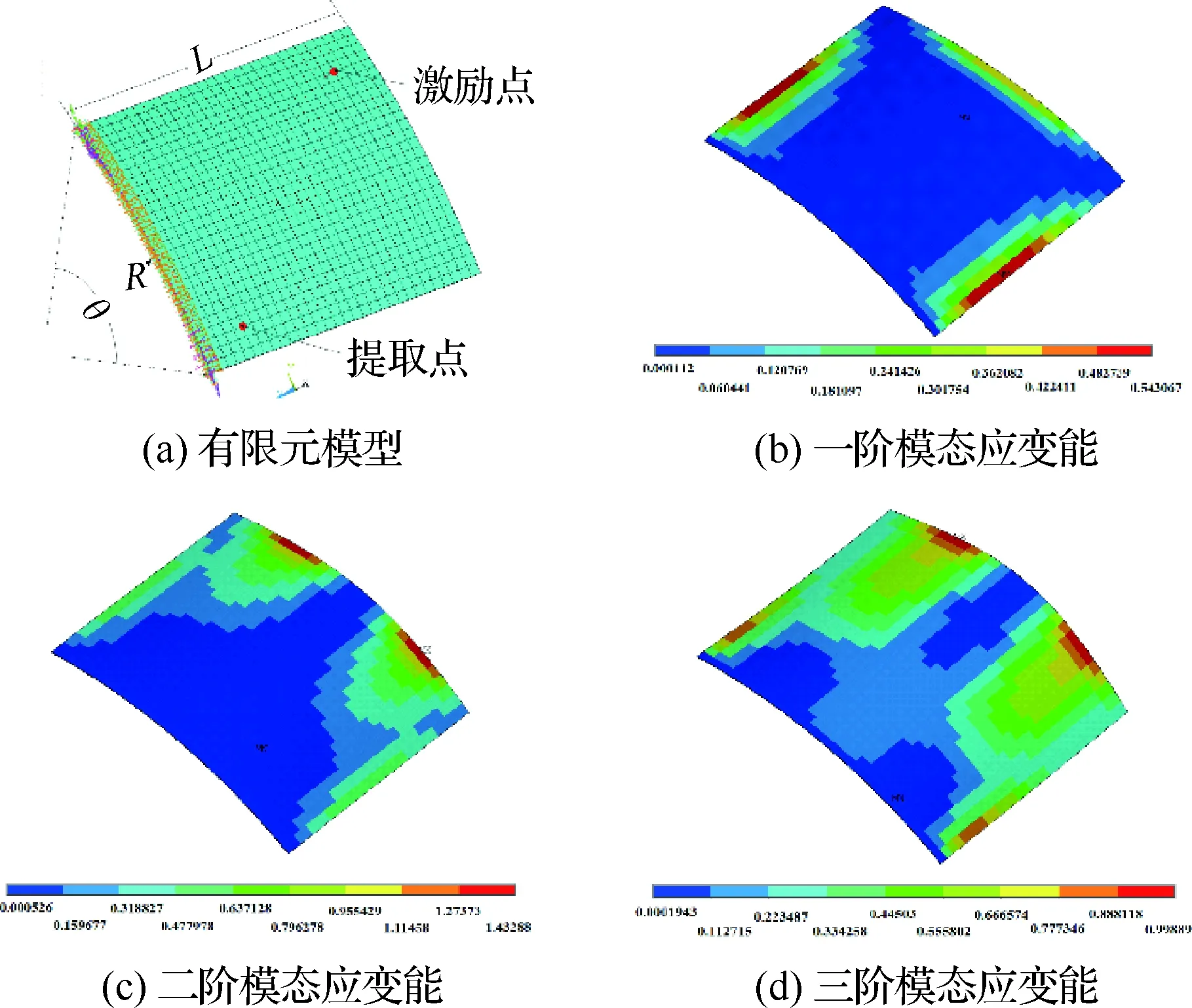
圖2 薄殼模型與應變能分布Fig.2 Element model and modal strain energy of constrained damping shells

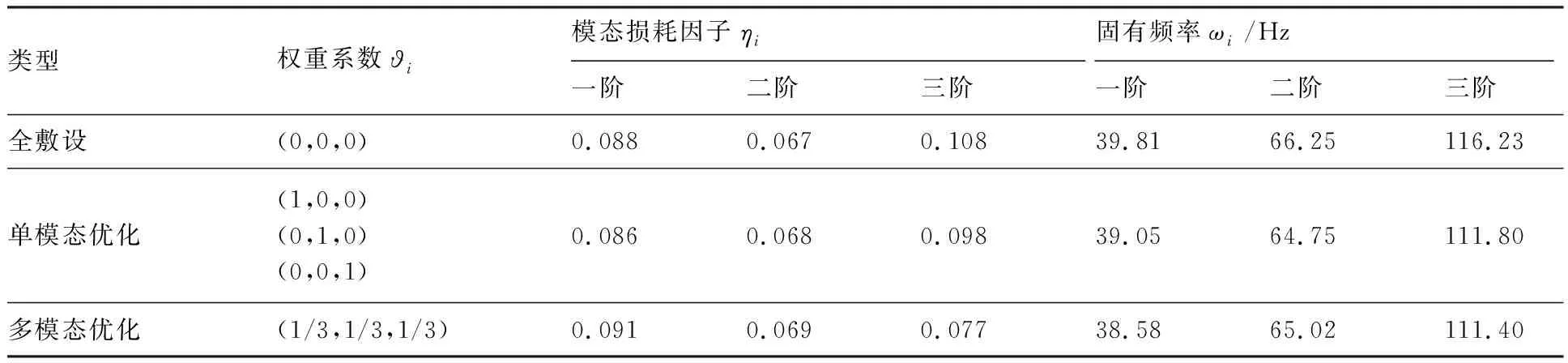
表1 不同權值薄殼結構模態損耗因子和固有頻率Table 1 Modal loss factors and natural frequency of single-shell structure

圖3(a)、圖3(b)與圖3(c)給出了針對前三階單模態優化函數拓撲構型迭代歷程。可見在前幾次迭代中，拓撲迭代曲線有大幅度的變化，均有先下降再上升的趨勢，說明了OC算法極值尋優的基本特性；同時拓撲構型云圖中出現了大量的中間密度，并開始顯現出優化拓撲構型的初始原貌。隨著迭代的進行，設計變量的中間值逐漸變少，向[0,1]兩端趨近(深藍色為0，紅色為1)，最終優化拓撲構型穩定清晰。它表明從整體上看迭代穩定前波動幅度較大，目標函數的尋優域范圍變化大，具有不單一變化于一極點而穩定的特點。進一步與圖2中應變能云圖對比分析，不難發現各階拓撲構型迭代過程中，密度值較大的阻尼約束單元優先分布于應變能相對較大的位置，密度值小的處于應變能較小的位置，隨著迭代的進行密度較大趨于1，表示敷設阻尼材料位置，密度較小多半趨于0，表示原基體。這主要由于應變能小的位置，黏彈性阻尼材料對振動能耗損相對較弱。從化增加，出現曲線的跌宕，這是由于隨著非最大應變處粘貼阻尼材料的進行，最大應變與小應變處交替迭代更新，拓撲結構阻尼約束單元出現了大微量的變化，使得尋優范圍擴大，出現了顯著的不局限于已有某一迭代極值點的優化過程。

根據振動理論，結構振動通常是由多階振型相互作用的結果，在工程實際中，常常是固有頻率最低的幾個振型的貢獻占了壓倒地位，多模態振動是承力件基本運動狀態。圖3(d)為多模態優化迭代歷程，從圖中可看出，偽密度值逐漸迭代至0或1，其數量比重增加，中間密度減少，穩定的減振拓撲構型漸顯。同樣可看出，高密度阻尼材料主要敷設在前三階應變能較大的交集區，反之，低密度阻尼材料在最小應變能的交集區。

進一步可看出，薄殼阻尼材料的減振優化迭代次數較少，便于形成灰度值少(產生于中間密度數量少)的拓撲構型，迭代至25次以上可達到尋優穩定狀態。不同的權值優化歷程圖均顯示，在第4次迭代左右出現了起伏較大的波動，且優化拓撲構型云圖趨向0值增多，這是由于集中于中間密度的趨勢減弱，兩級趨向性增強。在此基礎上，隨著迭代次數進一步增加，拓撲構型的灰度漸少，最終優化迭代至穩定的減振拓撲構型。

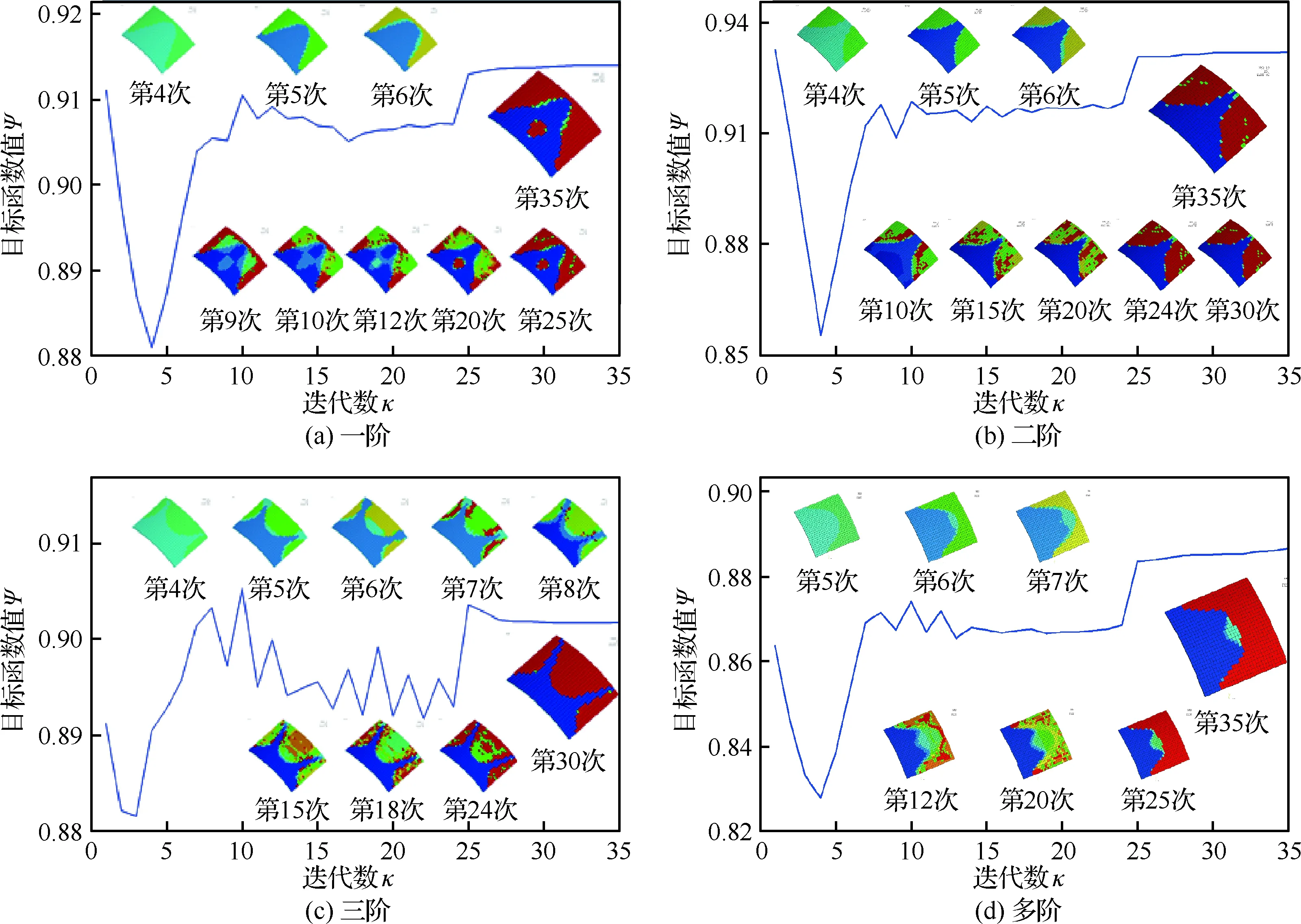
圖3 模態優化函數拓撲構型迭代歷程Fig.3 Iteration of modal optimization function and topology shape

對于不同權值函數，固有頻率優化迭代變化隨優化函數波動而改變。圖4給出了其變化歷程，各優化函數均以較小的波動范圍引起固有頻率的變化，變化差值在±5 Hz以內，因此模態損耗因子的優化不影響結構固有頻率和振型，并且滿足優化模型約束條件的給定值，優化穩定后的數值可見表1中給出前三階模態固有頻率。

隨著優化函數的迭代，不同階的模態損耗因子具有相應不同的變化。圖5給出了對應于不同階次優化函數的損耗因子迭代過程。從圖中可知損耗因子值初期遞增，隨后減小逐漸趨于穩定，以及其優化曲線變化與目標函數的數值關系式(6)

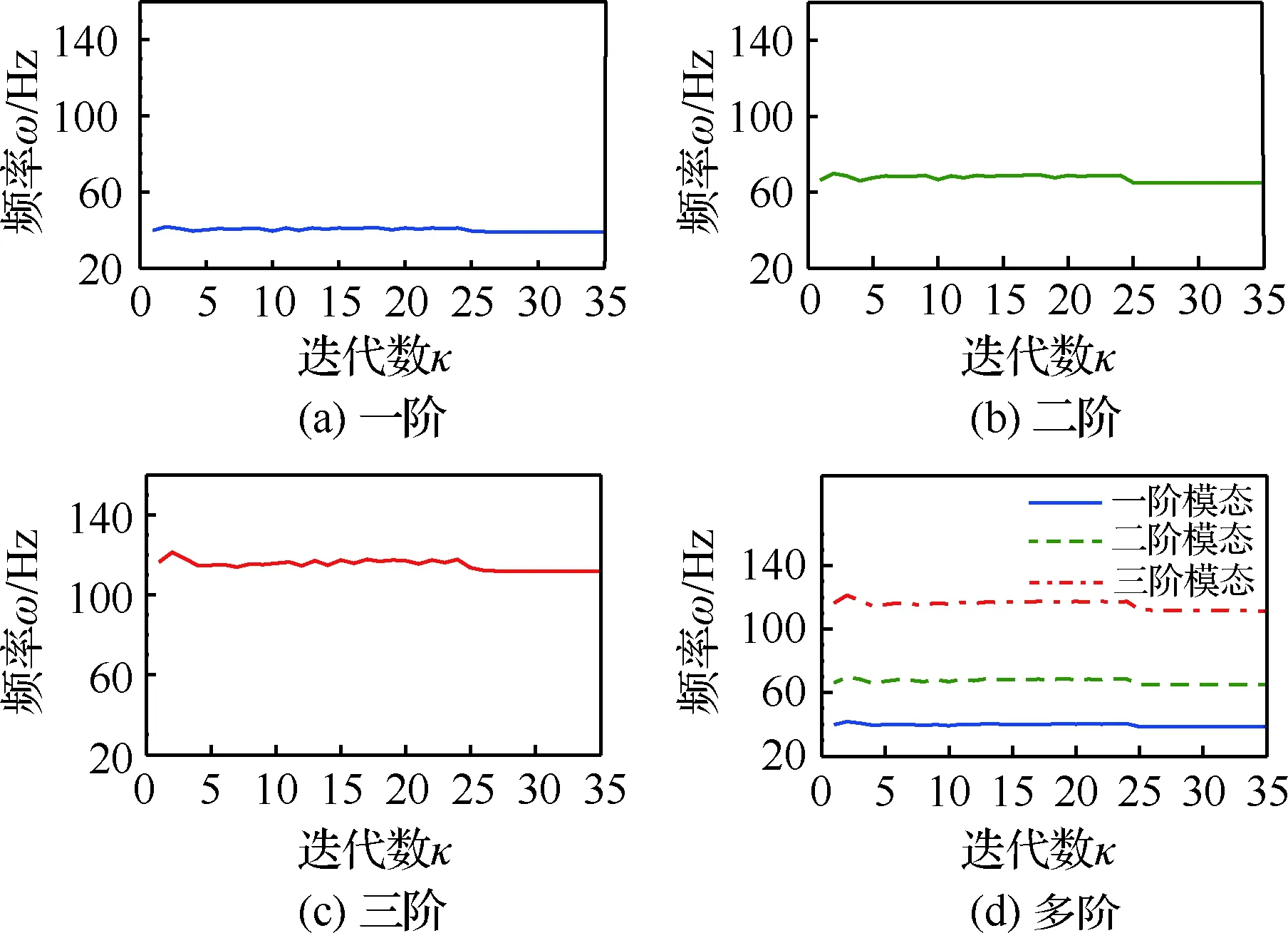
圖4 模態優化固有頻率迭代歷程Fig.4 Iteration of modal optimization natural frequency

圖5 模態優化損耗因子迭代歷程Fig.5 Iteration of modal optimization loss factor

保持一致。同時可得中間密度較為集中時，模態損耗因子的數值出現隨之增加的趨勢，相反趨于兩級或灰度值減少時，損耗因子呈現下降。這表明在目標函數值趨于穩定時，若灰度較多，雖表現出損耗因子增加或穩定，但由此提取的拓撲構型與計算的損耗因子相比會有所減小，導致結果存在虛增情況。在此，進一步驗證了抑制灰度值的重要性。

不難發現，圖3～圖5中在迭代25次附近曲線出現突變，呈現出上升的趨勢，緊接著趨于穩定變化。為了抑制灰度值的產生，并且使趨于1的或趨于0的偽密度分別為設計變量最小值χmin和最大值χmax，因此在算法迭代中可增大插值模型懲罰因子p和q，減小設計變量移動極限值λ，這樣可以在優化迭代穩定的后期減少中間密度材料的存在，提高拓撲構型約束阻尼層與實際所采用材料屬性的一致性。

圖6給出了針對靈敏度的正負數量的迭代跟蹤，提出靈敏度正數比=正數/總數，并以此作為度量分析。優化過程中起始迭代次數均以大于0.6的比值尋優，中間迭代數以低于0.6的比值尋優。反映了動力學優化中若僅以靈敏度負值參與迭代優化，難以滿足體積約束條件，會使尋優域縮小，表明靈敏度正負比值的波動性，可能引起出現極值點解和拓撲構型跳躍。

為此，采用一般優化準則法對上述算例展開拓撲減振優化。圖7(a)、圖7(b)和圖7(c)為一般法單模態優化迭代歷程。與圖3對比，可以看出在迭代優化初期，曲線變化比較相似，但從拓撲構型云圖上看一般法優化的中間密度數量較多，趨向于密度為0或1的變化減弱。可看出，圖7(a)在迭代10次附近、圖7(b)在迭代13次附近曲線出現明顯的下降，隨著中間密度值增多，優化拓撲構型反而出現倒退的現象，并結合圖6分析，可得能參與優化迭代的設計變量正數比明顯高于體積約束系數0.5，致使中間密度增加，且優化滿足不了減振優化模型的體積約束條件而迭代優化中止。

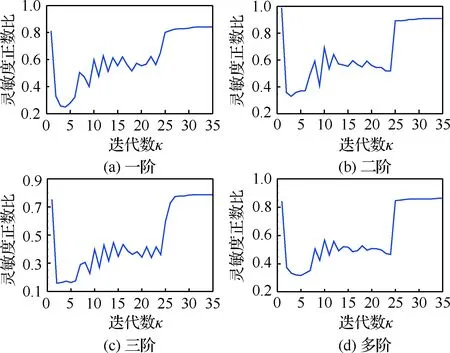
圖6 模態優化靈敏度正數比迭代歷程Fig.6 Iteration of modal optimization sensitivity positive ratio

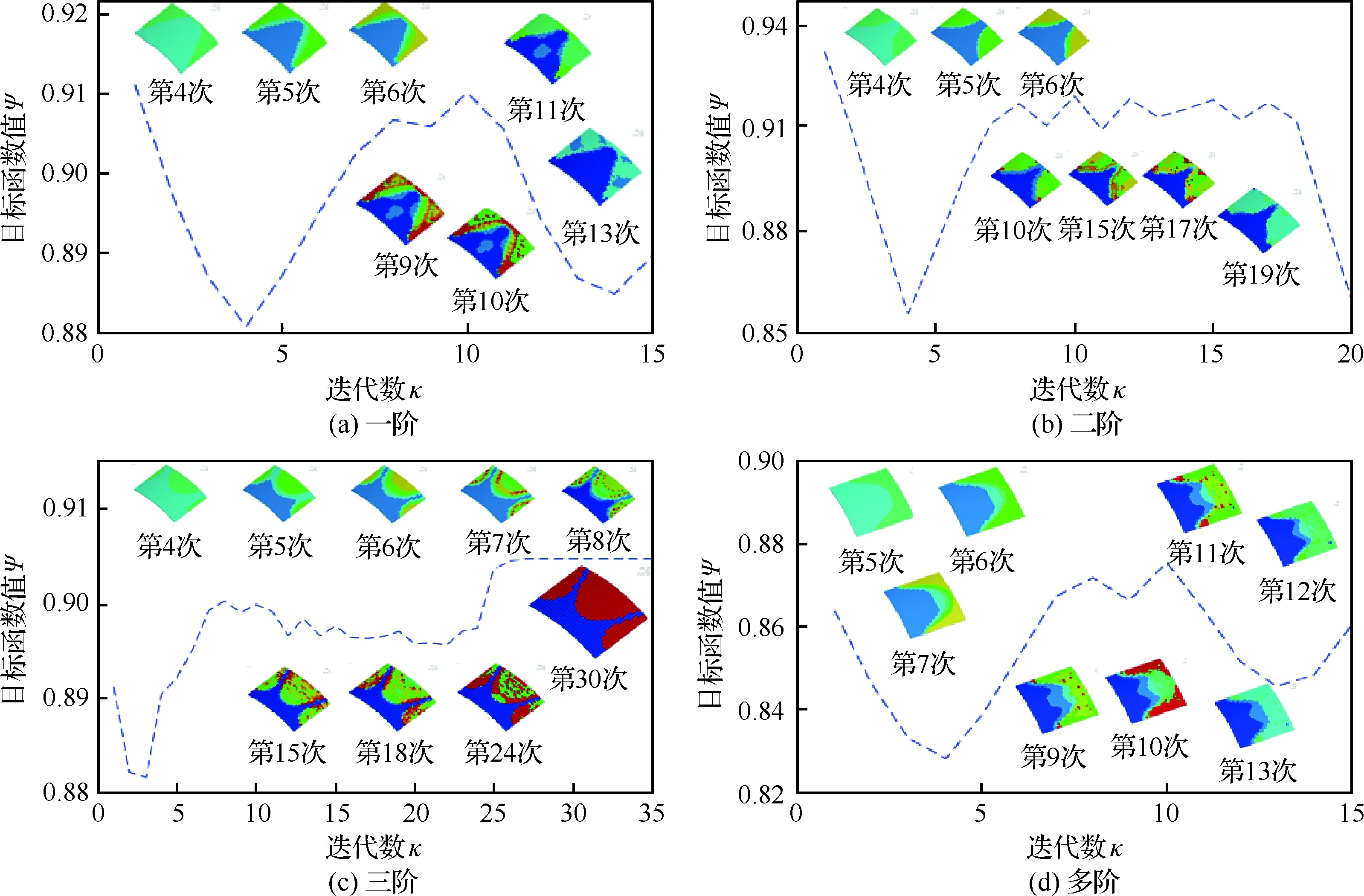
圖7 一般法模態優化拓撲構型迭代歷程Fig.7 Iteration of modal optimization function and topology shape by unimproved OC method

圖7(c)進一步表明一般法的參與設計變量正數比低于約束體積系數時，可進行迭代優化，中間密度較多，迭代變化平緩，反映出尋優極值點不易變化；從圖6(c)中可得到迭代后期出現不滿足約束條件的靈敏度正數比，但是在設計變量移動極限值的作用下，同樣能穩定拓撲構型。

圖7(d)給出了一般法多模態優化拓撲構型過程。同樣反映出與一般法單模態迭代優化中不易滿足體積約束條件的分析相一致的情況。

為了進一步驗證其算法的優化效果，采用不同權值拓撲構型作諧響應分析，且與全覆蓋約束阻尼層諧響應對比。圖8(a)、圖8(b)和圖8(c)為單階模態優化諧響分析曲線。與全覆蓋阻尼激勵幅值相比均有所增加，但增加的幅值較小，同時驗證了表1中模態損耗因子變化，在體積減少50%的前提下，一階和三階模態損耗因子下降2.3%、9.3%以及二階模損耗因子上升1.5%；圖8(d)給出了針對前三階多模態權值優化諧響分析曲線，另外結合表1中多模態優化特性數值，結果表明與單模態優化相比，有更好的減振效果，一階損耗因子增加相對而言較多，提升了一階單模態優化效果。優化阻尼和全覆蓋阻尼結構諧響應分析的共峰值激勵頻率與表1中優化前后固有頻率變化相一致，驗證了其合理性。不過，可看出未優化的高階模態減振幅值相對于全覆蓋阻尼有所增加，由于高階振型較復雜，與敷設在優化區域顯現較集中的已優化拓撲構型相比，減振效果有所減弱。

從優化前后幅頻特性曲線可以看出，第三階共峰值均相對較小，根據振動理論，可知激勵頻率與固有頻率較接近時其主振型起主導作用，并且圖2(a)所示的提取點位置處固有頻率主振型幅值較小，進而使未優化阻尼結構同樣出現較低的共振響應峰。

在優化體積減少50%的前提下，殼結構均能優化得到與全敷設約束阻尼材料同等的減振效果，甚至在低頻段優化效果有相對大的提升，結構的頻率和振型保持在約束范圍內，提高了結構的輕量化要求，改善結構減振控制中的穩定狀態。

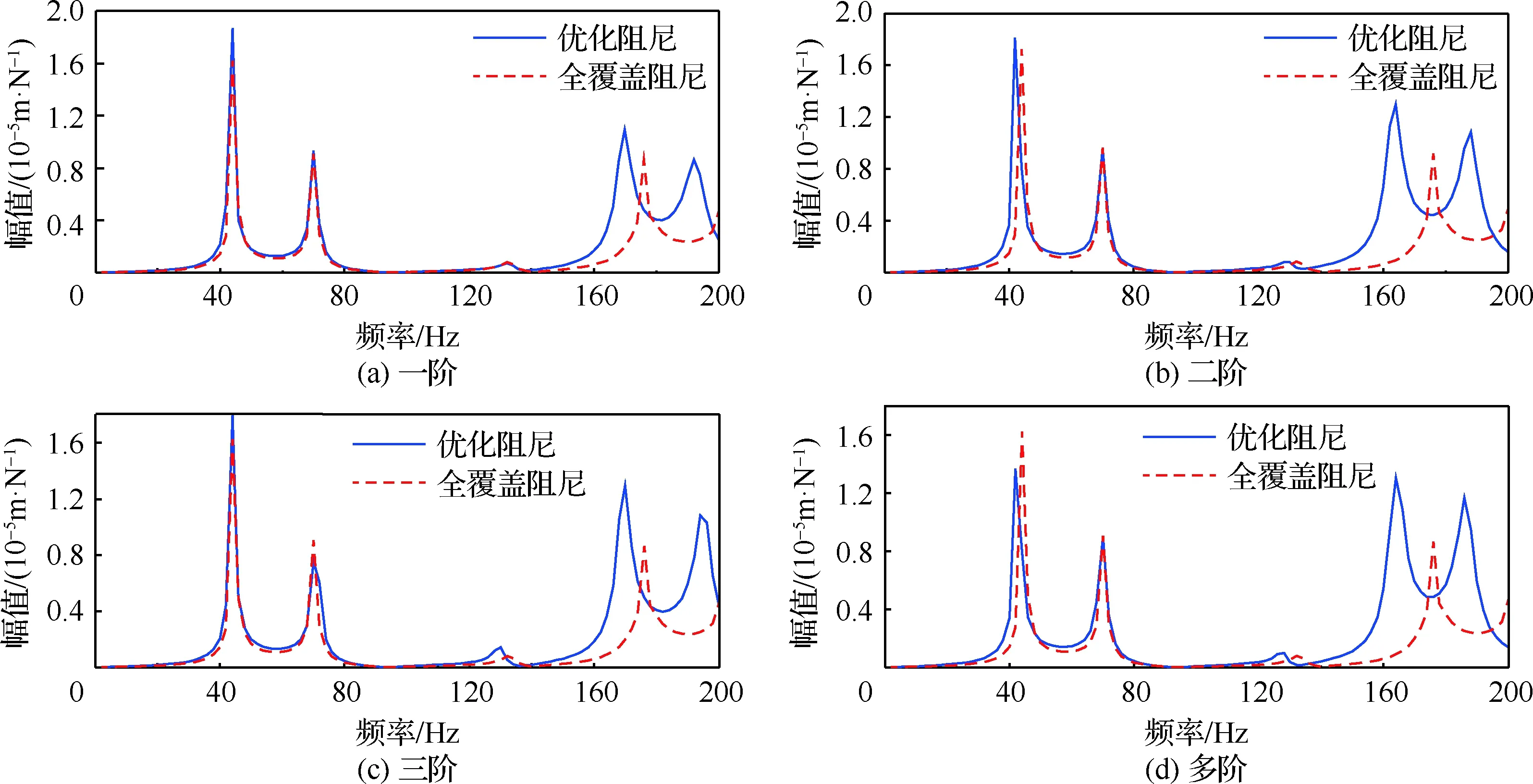
圖8 模態優化前后諧響應分析Fig.8 Harmonic response analysis of single shell mode optimiz

5 結 論

1) 以50%為體積約束條件，多階優于單階模態優化，得到與全覆蓋約束阻尼層相比，模態損耗因子偏差卻不超過10%的效果，亦可在合適減少材料的情況下，引起結構損耗因子提高，增加能量耗散，抑制振動響應。

2) 提出對靈敏度正數比的分析，反映出動力學優化中靈敏度正、負數集共存，優化中應避免非靈敏度全域優化迭代發生和拓撲構型跳躍。

3) 拓撲構型灰度越大，模態損耗因子越大，進而在優化過程中，避免因為出現懲罰不夠導致穩定構型包含較多中間密度值的情況發生，使得優化結果虛增，同時拓撲構型顯示可將約束阻尼材料較多敷設在振動響應大的區域，能夠最大限度的抑制振幅。

4) 全域靈敏度改進準則法對復合殼結構不同權值優化，驗證了算法具有迭代快、尋優域廣和拓撲構型清晰穩定的優勢。