基于變權重變異鴿群優(yōu)化的無人機空中加油自抗擾控制器設計
費倫,段海濱,2,*,徐小斌,鮑瑞,孫永斌
1. 北京航空航天大學 自動化科學與電氣工程學院, 北京 100083 2. 鵬城實驗室, 深圳 518000
空中加油 (Aerial Refueling) 技術是加油機在航行中為受油機補充燃料的技術,可以顯著提高戰(zhàn)斗機的續(xù)航能力[1]。在空中加油任務中,由于尾流等影響,需要受油機具有較高的控制精度,因此需要設計控制精度高、抗干擾能力強的控制系統(tǒng)。Nicol等[2]在2011年提出了一種直接近似的自適應控制方法,依靠一組先驗的權重來指導學習,從而更新控制器的權重。Enomoto等[3]在2008年采用內外環(huán)動態(tài)逆方法,設計了無人機制導跟蹤控制系統(tǒng),該系統(tǒng)能夠實現(xiàn)與目標無人機保持理想的相對距離。但動態(tài)逆系統(tǒng)控制器使用在空中加油的對接階段,會造成逆誤差,不能滿足對接階段的控制要求。Lungu[4]于2019年設計了一種基于動態(tài)反步控制的自動著陸飛行控制系統(tǒng),驗證了該控制結構在不同初始條件下的穩(wěn)定性和魯棒性,由于其控制算法需要基于準確的數(shù)學模型,其實現(xiàn)有一定的困難。
自抗擾控制(Active Disturbance Rejection Controll, ADRC)技術是Han在20世紀80年代所提出的一種新的控制理論,這種控制不依賴于受控對象的具體數(shù)學模型,具有很強的魯棒性和抗干擾性[5]。自抗擾技術廣泛地在控制工程領域應用[6-10]。相比于經(jīng)典的比例-積分-微分(Proportional-Integral-Derivative, PID)控制器,自抗擾控制器的控制效果更為優(yōu)越,系統(tǒng)的穩(wěn)健性更強。但自抗擾控制同樣存在控制器參數(shù)眾多,整定參數(shù)往往依靠工程經(jīng)驗等問題,不容易得到最優(yōu)控制效果[11]。
鴿群優(yōu)化(Pigeon Inspired Optimization, PIO)是在2014年提出的一種啟發(fā)式優(yōu)化仿生算法[12],該算法基于鴿群在飛行中尋找目標的行為機制。鴿群優(yōu)化算法由于具有收斂速度快、搜索效率高的優(yōu)勢,已得到廣泛應用[13]。文獻[14]在2014年將鴿群優(yōu)化算法引入模擬退火算法思想,用于解決低空無人機目標檢測問題。文獻[15]在2015年將其運用在航天器的最優(yōu)編隊重構問題。文獻[16]在2018年在線滾動時域控制中應用鴿群優(yōu)化算法。但針對參數(shù)整定等多維優(yōu)化問題,在鴿子的數(shù)目、尋優(yōu)迭代次數(shù)較少的情況下,經(jīng)典的鴿群優(yōu)化算法容易出現(xiàn)陷入局部最優(yōu)、迭代后期收斂速度過慢等問題。
本文提出了一種變權重變異鴿群優(yōu)化(Variable Weighted Mutant Pigeon Inspired Optimization, VWMPIO)算法,將反向變異操作加入到地圖和指南針算子中,從而降低了鴿群尋優(yōu)陷入局部最優(yōu)解的概率。自適應權值能夠增加處于較優(yōu)位置的鴿子在鴿群中的權重,相比經(jīng)典的鴿群優(yōu)化算法能夠提高算法尋優(yōu)的效率,從而提高無人機的姿態(tài)控制水平。
本文以F-16的公開數(shù)據(jù)為基礎,建立無人機模型,通過MATLAB/SIMULINK進行建模仿真。仿真平臺包括無人機六自由度非線性模型。本文首先根據(jù)自主空中加油的特點,基于自抗擾技術設計了姿態(tài)穩(wěn)定控制器的結構。為解決人工整定參數(shù)困難的問題,獲得最佳的控制效果,使用變權重變異鴿群優(yōu)化算法進行尋優(yōu),并與傳統(tǒng)的啟發(fā)優(yōu)化算法進行對比分析。
1 無人機六自由度數(shù)學模型
無人機通過調整升降舵、副翼和方向舵的角度,改變無人機的俯仰角、偏航角和俯仰角大小。構建無人機的六自由度運動學與動力學模型為
(1)
式中:p、q、r為無人機滾轉角速度、俯仰角速度及偏航角速度;φ、θ、ψ為無人機的滾轉角、俯仰角與偏航角;Ix、Iy、Iz分別為無人機繞機體軸的轉動慣量;3個力矩分量為滾轉力矩L、俯仰力矩M、偏航力矩N,其表達式為

(2)

無人機空中加油過程中,受油機受到加油機尾流等風干擾因素影響,同時空中加油任務的特殊性要求受油機跟蹤快速運動的錐套。由于固定翼無人機系統(tǒng)具有欠驅動、強耦合的特點,處理好空中加油任務中控制器的控制精度與響應速度是控制器設計的難點。
2 無人機自抗擾控制器
2.1 自抗擾控制器結構設計
自抗擾控制器由跟蹤微分器(Tracking Differentiator, TD)、擴張狀態(tài)觀測器(Extended State Observer, ESO)和非線性狀態(tài)誤差反饋控制律(NonLinear State Error Feedback, NLSEF) 3部分構成[17]。自抗擾控制器結構如圖1所示。

圖1 自抗擾控制器的結構Fig.1 Structure of ADRC controller
對于系統(tǒng)模型中的不確定性與外部的擾動,利用擴張狀態(tài)觀測器進行估計與補償,從而抑制系統(tǒng)干擾。在基于自抗擾控制的無人機俯仰角、滾轉角控制律以及偏航角的增穩(wěn)控制律設計中采用相同的控制策略。基于自抗擾控制器的無人機姿態(tài)控制律結構框圖如圖2所示。將無人機姿態(tài)方程整理為符合自抗擾理論的對應形式如式(3)所示。

圖2 無人機姿態(tài)控制律結構框圖Fig.2 Diagram of attitude control law of UAV
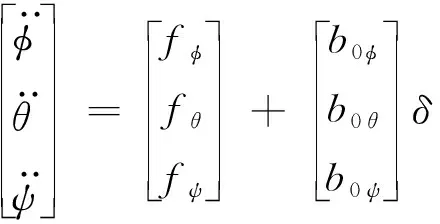
(3)
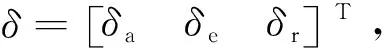
(4)
2.2 自抗擾控制器算法設計
1) 跟蹤微分器
跟蹤微分器的輸出變量v1跟蹤輸入指令信號v0,輸出變量v2是輸出變量v1的微分。跟蹤微分器的離散形式為
(5)
式中:r0為決定跟蹤速度的速度因子;h0為濾波因子;h為時間步長,單位為s;fhan(·)為最速控制綜合函數(shù),表達式如式(6)所示;sign(·)為符號函數(shù),其表達式如式(7)所示。
(6)

(7)
速度因子r0越大,跟蹤器的跟蹤效果就越快,反之則可以避免超調,因此選擇合適的速度因子可以實現(xiàn)無超調的快速跟蹤。濾波因子h0能夠濾掉跟蹤信號的噪聲部分,對含有噪聲或不連續(xù)的輸入也可以得到平滑的跟蹤信號,從而提高了系統(tǒng)控制的魯棒性。對于無人機的控制來說,跟蹤微分器可使控制器快速無超調地跟隨指令,且輸入保持連續(xù)光滑,減少無人機系統(tǒng)受突變指令信號的影響,從而避免機體抖振的出現(xiàn)。
2) 擴張狀態(tài)觀測器

(8)
式中:e為觀測值與狀態(tài)的誤差量;fal(·)為非線性函數(shù),其非線性的程度由α01、α02決定;β01、β02、β03為擴張狀態(tài)觀測器的增益;α01、α02一般取值為0.5與0.25,β01取值100[18]。fal(·)能夠實現(xiàn)工程中所需要的 “小誤差大增益,大誤差小增益”的良好功能;δ表示其線性區(qū)間的寬度,在實際系統(tǒng)中,一般取為0.02 左右[6],α為冪次,反映了觀測器的非線性程度。其表達式如式(9)所示。
(9)
3) 擾動補償過程
在誤差反饋控制量u0基礎上,將觀測到的擾動量用于補償,控制量如式(10)所示。對擴充觀測的補償能夠使得控制器實現(xiàn)抗擾。
(10)
4) 非線性狀態(tài)誤差反饋律

(11)
式中:β1、β2分別為非線性誤差反饋的比例和微分的增益,相當于PID控制器中的增益參數(shù)。δ1的作用與擴張狀態(tài)觀測器中類似,本文取值為0.5。
在調節(jié)控制器參數(shù)時,r0、h0、β02、β03、a11、a12、β11、β12、b0等9個參數(shù)需根據(jù)系統(tǒng)實際需求變化。
3 變權重變異鴿群優(yōu)化算法的設計
3.1 經(jīng)典鴿群優(yōu)化算法
鴿群算法由兩個獨立的迭代循環(huán)組成,在每個循環(huán)中使用不同的算子模型,模擬鴿子在飛行不同階段使用不同的導航工具。

(12)
式中:R為地圖因子;rand為數(shù)值在0到1之間的隨機數(shù);t為當前迭代的代數(shù);Xgbest為上一次迭代中全局最好的位置。當算子循環(huán)次數(shù)達到NC1max后停止,進行下一個算子的操作。
地標算子(Landmark Operator)模仿鴿子利用地標導航的過程。地標算子如式(13)~式(15)所示更新。
(13)
(14)
Xi(t)=Xi(t-1)+rand·(Xgbest-Xi(t-1))
(15)
式中:NN為每一代中鴿子的總數(shù);Xcentre(t)為第t代鴿子的群體中心位置;fitness(·)為鴿子所在位置的適應度函數(shù)。鴿群的數(shù)目按照式(15)更新。其中,處于適應度函數(shù)較差位置的鴿子會被舍棄。當算子循環(huán)次數(shù)達到NC2max次后,結束鴿群優(yōu)化算法。
3.2 對經(jīng)典鴿群優(yōu)化算法的改進
鴿群優(yōu)化雖然具有較快的收斂速度,當搜索范圍復雜、搜索空間的維數(shù)較大時,搜索結果容易落入局部最優(yōu)。為提高其在解決無人機控制問題時的精確性,本文從兩個方面對經(jīng)典鴿群優(yōu)化模型的地圖和指南針算子進行了改進。
在經(jīng)典的鴿群優(yōu)化公式中,權重ω=e-Rt隨著時間的演化,調節(jié)鴿群的全局和局部搜索能力。受粒子群算法啟發(fā),對于復雜尋優(yōu)問題,智能體間的信息共享能力比單個個體的搜尋功能更重要[19]。慣性權重高則全局的搜索能力較好,而慣性權重低能夠獲得局部搜索能力的加強[20]。但經(jīng)典鴿群優(yōu)化對所有鴿子均賦相同權重,沒有考慮每只鴿子所處位置之間的差異。因此,本文設計了一種自適應的非線性有界遞減權重,如式(16)所示。
(16)
式中:R和經(jīng)典鴿群優(yōu)化的定義相同;fitness(Xi)和fitness(Xgbset)為第i只鴿子和全局最優(yōu)鴿子的適應度函數(shù)。在算法執(zhí)行過程中,權重的初始值為e-R,并隨著迭代連續(xù)有界下降,這與經(jīng)典鴿群優(yōu)化算法在初期具有較大的搜索范圍、后期快速收斂的特性一致。同時,鴿子自身位置適應度函數(shù)和當前最優(yōu)位置適應度函數(shù)之比反映了不同鴿子間的位置差異,用于調整權值,使得鴿群更好地收斂到最優(yōu)解。
在廣泛搜索的地圖和指南針算子階段,我們希望鴿子能夠跳出局部最優(yōu)值。對于適應度最差的鴿子,由于其與當前最優(yōu)鴿子距離較遠,按照經(jīng)典鴿群優(yōu)化算法對于尋優(yōu)過程的貢獻較低。因此將適應值最差的鴿子的速度設定為當前全局最優(yōu)鴿子Xgbset的反方向,這樣能夠增加鴿群的多樣性。經(jīng)過反向變異操作后,鴿群提高了全局的搜索能力,更容易在前期跳出局部最優(yōu)。適應值最差的鴿子的更新如式(17)所示。
(17)
無人機的控制目標是使無人機的姿態(tài)在較短時間內盡可能快速、精準地跟隨指令,因此適應度函數(shù)中應當包括姿態(tài)角指令和無人機的真實姿態(tài)。本文選取時間乘絕對誤差積分準則(ITAE)誤差準則[21]作為優(yōu)化算法的適應度函數(shù)。適應度函數(shù)的值越小,說明鴿子所處的位置越優(yōu)越。用ITAE誤差作為優(yōu)化的適應度函數(shù)為
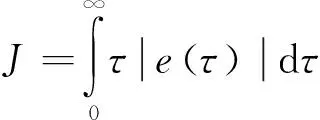
(18)
式中:τ為系統(tǒng)運行的時間;e(·)為無人機姿態(tài)角指令和真實姿態(tài)之間的誤差;J為誤差的評價函數(shù),用作優(yōu)化算法的適應度函數(shù)。按照本節(jié)提出的改進,本文所提出的變權重變異鴿群優(yōu)化算法的流程圖如圖3所示。

圖3 變權重變異鴿群優(yōu)化算法的流程圖Fig.3 Flowchart of VWMPIO
4 仿真及分析
本文使用MATLAB/SIMULINK仿真工具,搭建自抗擾控制器模型,并與經(jīng)典的串級PID控制器的仿真效果比較。首先,本文測試俯仰角通道的控制性能,選取俯仰角指令的角度為5°,選取控制步長為0.02 s,并于經(jīng)典PID的控制器進行比對。通過實驗,選擇自抗擾控制器粗調參數(shù)如表1所示。2種控制器的控制效果如圖4所示。
對2種控制器分別加入等幅的高斯噪聲,測試2種控制器的抗干擾能力,其輸出曲線如圖5所示。

表1 自抗擾俯仰控制通道粗調參數(shù)
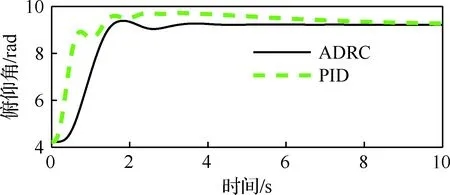
圖4 俯仰通道PID和ADRC控制器輸出曲線Fig.4 Output curves of pitch channel of PID and ADRC controller

圖5 干擾下的俯仰通道PID和ADRC控制器 輸出曲線Fig.5 Output curves of pitch channel of PID and ADRC controller under disturbance
分析圖4和圖5可以發(fā)現(xiàn),自抗擾控制器的過渡時間小于PID控制器,超調量也更小,對噪聲的抑制效果顯著。
本文使用變權重變異鴿群優(yōu)化整定控制器的參數(shù),優(yōu)化的結果與粒子群優(yōu)化算法及經(jīng)典鴿群算法進行對比,優(yōu)化算法適應度函數(shù)均采用上述的ITAE誤差。對于俯仰角控制通道,對r0、h0、β02、β03、a11、a12、β11、β12、b0等9個參數(shù)進行優(yōu)化,其他參數(shù)設定保持不變。首先需要對各優(yōu)化算法的狀態(tài)參數(shù)進行初始化操作,粒子群算法的參數(shù)如表2所示,經(jīng)典和變權重變異鴿群優(yōu)化的參數(shù)如表3所示。自抗擾控制器經(jīng)過變權重變異鴿群優(yōu)化算法的優(yōu)化后,其控制性能得到了進一步的提高,各參數(shù)的迭代曲線與優(yōu)化后的仿真結果如表4和圖6~圖10所示。

表2 粒子群算法初始參數(shù)Table 2 Initial parameters of PSO

表3 鴿群優(yōu)化、變權重變異鴿群優(yōu)化算法初始參數(shù)Table 3 Initial parameters of PIO and VWMPIO
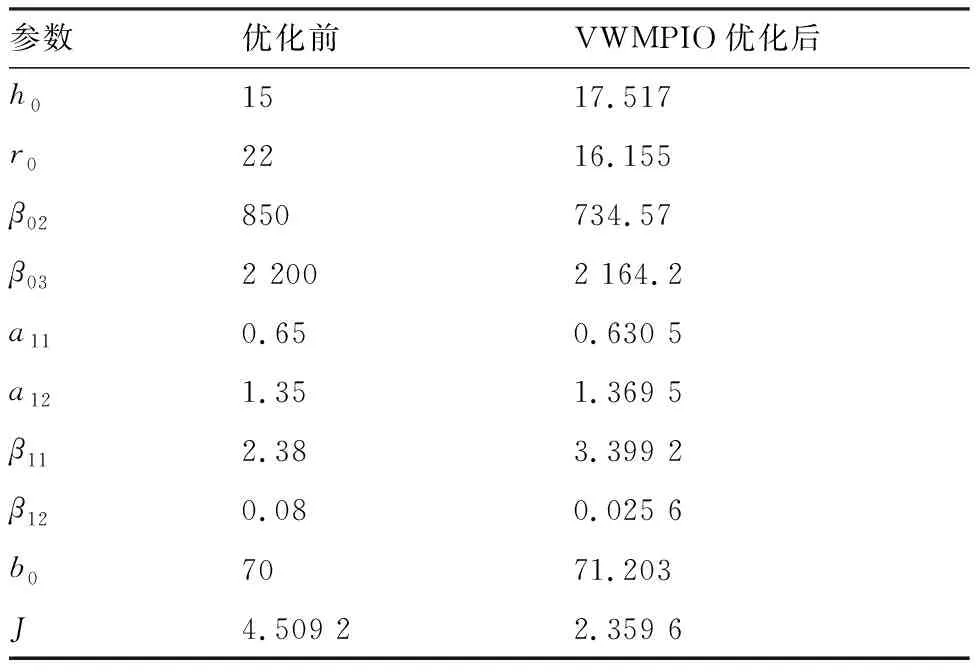
表4 俯仰通道變權重變異鴿群優(yōu)化前后的參數(shù)對照

圖6 俯仰通道適應度函數(shù)優(yōu)化曲線Fig.6 Optimization curves of fitness function of pitch channel

圖7 俯仰通道r0、h0優(yōu)化曲線Fig.7 Optimization curves ofr0and h0 of pitch channel

圖8 俯仰通道β02、β03和b0優(yōu)化曲線Fig.8 Optimization curves ofβ02, β03 and b0 of pitch channel
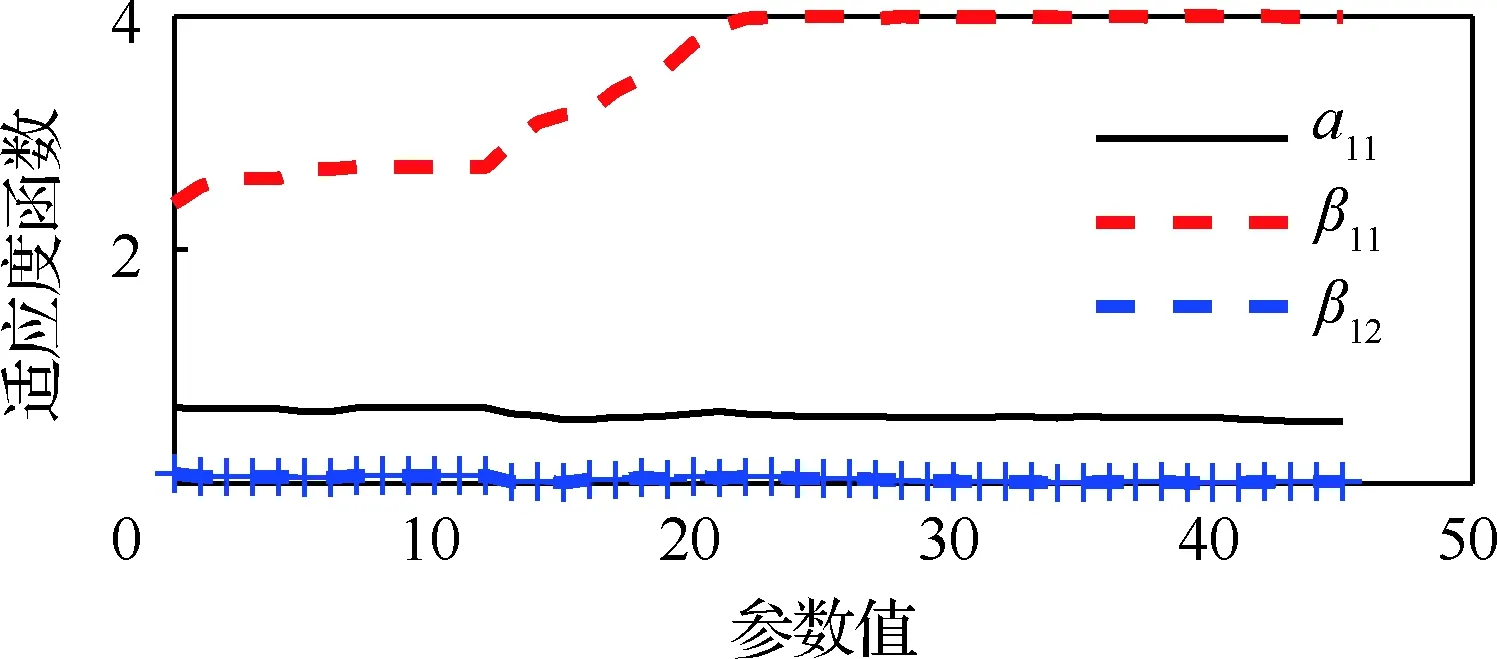
圖9 俯仰通道a11、β11、β12優(yōu)化曲線Fig.9 Optimization curves ofa11 andβ11 and β12of pitch channel

圖10 ADRC控制器優(yōu)化前后輸出曲線Fig.10 Output curves of ADRC controller before and after optimization
對比變權重變異鴿群優(yōu)化算法與粒子群算法、普通鴿群優(yōu)化算法的優(yōu)化結果,變權重變異鴿群優(yōu)化算法在尋優(yōu)的早期階段可以快速收斂,且最終收斂的位置比粒子群算法和普通鴿群優(yōu)化算法要優(yōu)越。
本文接下來優(yōu)化橫滾和偏航通道參數(shù)。仿照俯仰角通道的優(yōu)化,同樣選取控制周期為0.02 s,優(yōu)化算法的初始鴿群參數(shù)如表2和表3所示。設定滾轉角指令角度為5°,滾轉角控制通道跟隨指令,控制回路偏航角通道為無人機的橫側向運動進行增穩(wěn)。各優(yōu)化算法的初始狀態(tài)參數(shù)與俯仰通道保持一致,優(yōu)化前后的參數(shù)分別如表5,參數(shù)對比曲線如圖11~圖18,仿真結果如圖19所示。

表5 橫滾、偏航通道變權重變異鴿群優(yōu)優(yōu)化前后參數(shù)對照

圖11 橫滾通道適應度函數(shù)優(yōu)化曲線Fig.11 Optimization curve of fitness function of roll channel
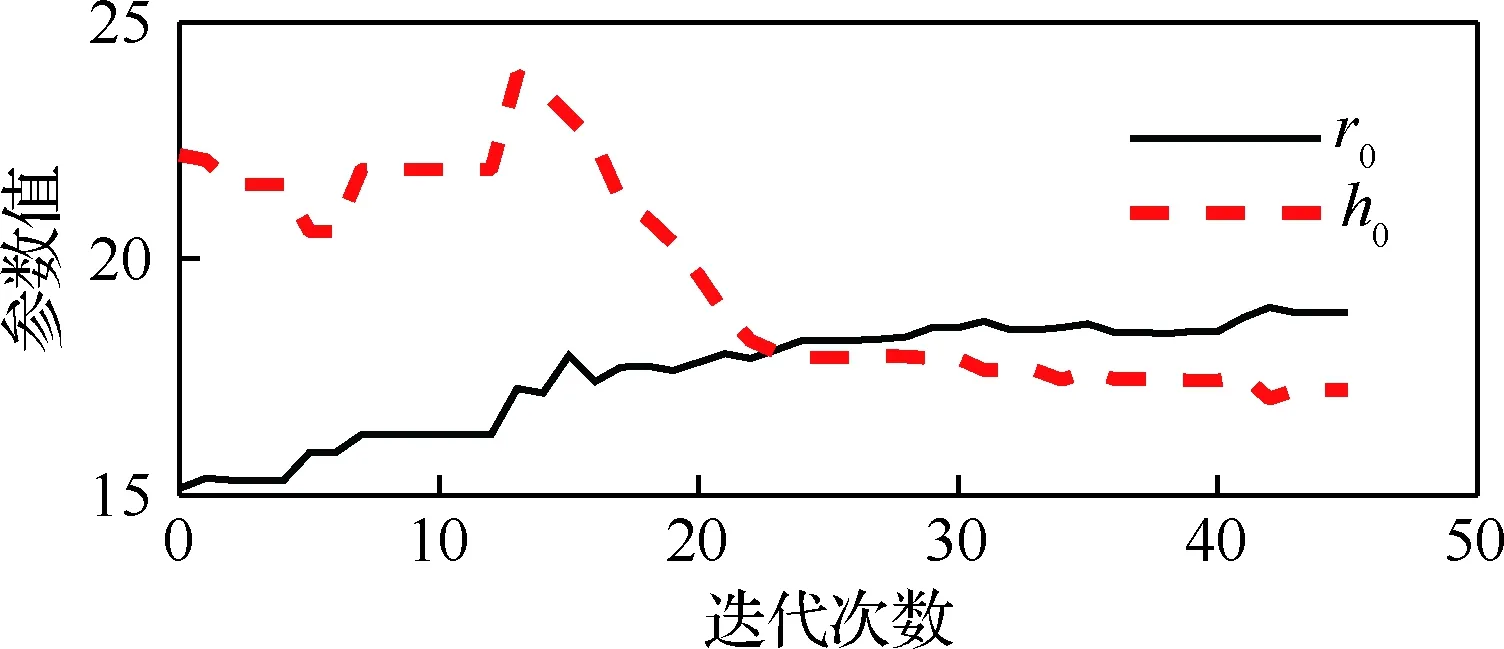
圖12 橫滾通道r0、h0優(yōu)化曲線Fig.12 Optimization curve ofr0and h0 of roll channel
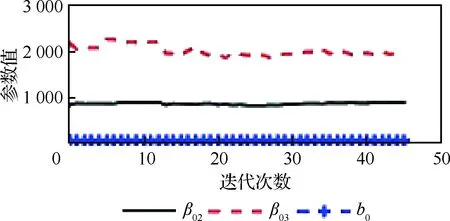
圖13 橫滾通道β02、β03和b0優(yōu)化曲線Fig.13 Optimization curve ofβ02, β03 and b0 of roll channel

圖14 橫滾通道a11、β11、β12優(yōu)化曲線Fig.14 Optimization curve of a11, β11 and β12 of roll channel

圖15 偏航通道適應度函數(shù)優(yōu)化曲線Fig.15 Optimization curve of fitness function of yaw channel
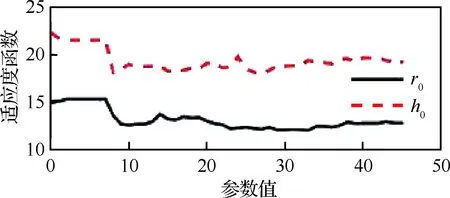
圖16 偏航通道r0、h0優(yōu)化曲線Fig.16 Optimization curve of r0 and h0 of yaw channel
橫滾和偏航通道的控制結果得到了一定的改善,橫滾和偏航通道的結果驗證了本文提出的算法的可行性。

圖17 偏航通道β02、β03和b0優(yōu)化曲線Fig.17 Optimization curve of β02, β03 and b0of yaw channel

圖18 偏航通道a11、β11、β12優(yōu)化曲線Fig.18 Optimization curve of a11, β11 and β12 of yaw channel

圖19 ADRC優(yōu)化前后和PID控制器控制效果對比Fig.19 Output curve of ADRC controller before and after optimization and PID controller
5 結 論
1) 本文設計了一種基于自抗擾控制技術的無人機的姿態(tài)增穩(wěn)控制器。利用F-16模型進行了仿真實驗,與經(jīng)典的PID控制算法對比,本文設計的自抗擾控制器的控制精度較高,對噪聲和擾動有著較好的抑制效果。
2) 與傳統(tǒng)的優(yōu)化算法相比,本文所設計的變權重變異鴿群優(yōu)化算法保持了鴿群優(yōu)化快速收斂的優(yōu)點,并能夠有效降低優(yōu)化陷入局部最優(yōu)的概率,且該算法容易實現(xiàn),可提高無人機姿態(tài)控制的性能。

