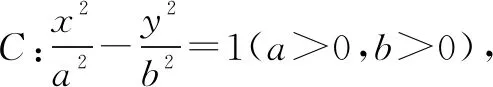圓錐曲線(xiàn)中直線(xiàn)過(guò)定點(diǎn)問(wèn)題探析
胡貴平
(甘肅省白銀市第一中學(xué) 730900)
“定點(diǎn)”問(wèn)題是圓錐曲線(xiàn)常考題型,注重知識(shí)的綜合,更注重?cái)?shù)學(xué)思想方法,難度較大,縱觀近幾年高考,圓錐曲線(xiàn)中直線(xiàn)過(guò)定點(diǎn)問(wèn)題頻頻出現(xiàn),下面類(lèi)比探析其相似性.
命題1 已知拋物線(xiàn)C:y2=2px(p>0),過(guò)定點(diǎn)(t,0)(t>0)且不垂直于x軸的直線(xiàn)l與拋物線(xiàn)C交于M,N兩點(diǎn),則在x軸上存在點(diǎn)P(-t,0),使得∠OPM=∠OPN.
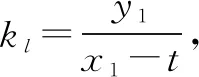
例1(2018全國(guó)新課標(biāo)Ⅰ文)設(shè)拋物線(xiàn)C:y2=2x,點(diǎn)A(2,0),B(-2,0),過(guò)點(diǎn)A的直線(xiàn)l與C交于M,N兩點(diǎn).

圖1
(1)當(dāng)l與x軸垂直時(shí),求直線(xiàn)BM的方程;
(2)證明:∠ABM=∠ABN.
解(1)當(dāng)l與x軸垂直時(shí),l的方程為x=2,代入y2=2x, ∴M(2,-2),N(2,2)或M(2,2),N(2,-2),∴BM的方程為:2x+x+2=0或2y-x-2=0.
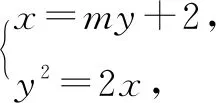
∴kBM=-kBN,∴∠ABM=∠ABN.
拓展已知拋物線(xiàn)C:y2=2px(p>0),過(guò)定點(diǎn)(t,0)(t<0)且不垂直于x軸的直線(xiàn)l與拋物線(xiàn)C交于M,N兩點(diǎn),則在x軸上存在點(diǎn)P(-t,0),使得∠OPM+∠OPN=180°.
命題2 已知拋物線(xiàn)C:y2=2px(p>0),點(diǎn)P(-t,0)(t>0).設(shè)不垂直于x軸的直線(xiàn)l與拋物線(xiàn)C交于M,N兩點(diǎn),若∠OPM=∠OPN,則直線(xiàn)l過(guò)定點(diǎn)(t,0).

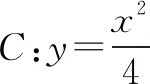
(1)當(dāng)k=0時(shí),分別求C在點(diǎn)M和N處的切線(xiàn)方程;
(2)y軸上是否存在點(diǎn)P,使得當(dāng)k變動(dòng)時(shí),總有∠OPM=∠OPN?說(shuō)明理由.
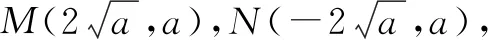
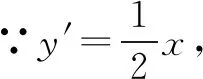
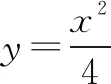
(2)存在符合題意的點(diǎn).證明如下:
設(shè)P(0,b)為符合題意的點(diǎn),M(x1,y1),N(x2,y2),直線(xiàn)PM,PN的斜率分別為k1,k2.
將y=kx+a代入C的方程整理得x2-4kx-4a=0.
∴x1+x2=4k,x1x2=-4a.
當(dāng)b=-a時(shí),有k1+k2=0,則直線(xiàn)PM的傾斜角與直線(xiàn)PN的傾斜角互補(bǔ),故∠OPM=∠OPN,所以P(0,-a)符合題意.


得(b2+a2k2)x2-2a2k2tx+a2(k2m2-b2)=0,
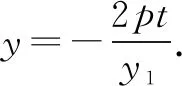
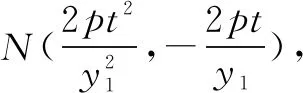
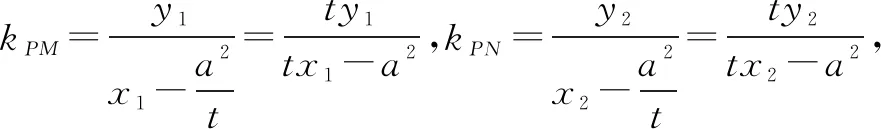



圖2
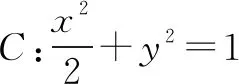
(1)當(dāng)l與x軸垂直時(shí),求直線(xiàn)AM的方程;
(2)設(shè)O為坐標(biāo)原點(diǎn),證明:∠OMA=∠OMB.
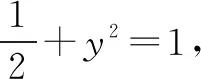



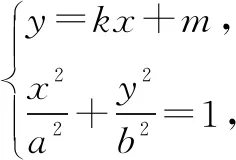

(1)求橢圓C的方程;
(2)已知A,B為橢圓長(zhǎng)軸的兩個(gè)端點(diǎn),作不平行于坐標(biāo)軸且不經(jīng)過(guò)右焦點(diǎn)F的直線(xiàn)PQ,與橢圓交于P,Q兩點(diǎn),若滿(mǎn)足∠AFP=∠BFQ,求證:直線(xiàn)PQ橫過(guò)一定點(diǎn).
解(1)依題意知l:y=x-c, ①