重視運用對稱 解決代數問題

楊紅余

(甘肅省平涼市第四中學 744000)

數學中蘊含大量的對稱思想，借助對稱思想，利用對稱的特性，可以實現初中數學中較典型的問題的求解.針對涉及到對稱的問題，要對問題的關鍵字眼保持一定的敏感性，如題目中包含存在關系、邏輯關系，尤其是位置關系的對稱時，就可以優先考慮利用對稱解決問題.

一、利用對稱性，求解函數最值問題

函數最值的求解方法比較多，可借助具體的數值來確定最值大小，也可以借助有關函數圖形進行考慮.每種方法有其使用的范圍，當問題出現兩個甚至多個代數和是一個定值，求解滿足一定關系式的函數值時，可以考慮從對稱的角度去解決.

例1已知a>0,b>0，且z=ab，若a+b=2時，求z的最大值.

解析觀察發現a+b=2，即意味著a,b的和是個定值，因此當a越大時，對應的b就越小；a越小時，相對應的b的取值就越大.若是a,b兩個取值相等，則意味著a,b在關系上是相互對稱的.因此，可以巧妙借助a,b這種相互對稱的關系，可以令a=1-r,b=1+r，此時始終滿足a+b=2的條件.最后，z=ab就等價轉化為z=(1-r)(1+r)=1-r2.由于r2永遠是不小于0的，所以只有r=0時，z能夠取到最大值，是1.具體解題如下：設a=1-r,b=1+r，則z=ab=(1-r)(1+r)=1-r2，又r2≥0，所以z=1-0=1，即z的最大值是1.

反思此題借助對稱性，將a,b用特殊的式子進行表示，實現問題的簡化.若采用常規的方法用b=2-a進行表示，并代入z=ab中，結合自變量a>0以及二次函數的性質也能求解.但有些同學會將z=-a2+2a開口方向弄錯，進而造成結果的錯誤.如果問題變成a,b,c,d均大于0，且a+b+c+d=2，求z=abcd的最大值時，利用對稱性解題就比較簡單.

二、依靠對稱性，判斷函數值的大小

有關兩個函數值的大小，常常是將兩個函數值求出來，然后再斷大小；也可以借助圖象進行輔助.但是，當函數值不便求解，甚至無法根據已知條件求出具體值時，不妨借助函數的對稱性質，進行綜合考慮.

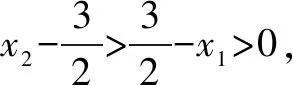
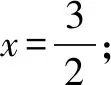
反思借助對稱判斷點關于對稱軸的位置關系，然后借助位置判斷大小，不過還需要掌握函數y=x2-3x-2的圖象開口方向，然后才能借助距離判斷函數值大小.

三、運用對稱性，證明不等式

在許多代數問題中都包含對稱思想，從對稱角度出發，借助對稱的有關性質，可以降低不等式的證明難度.

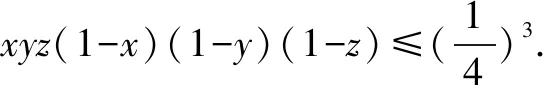
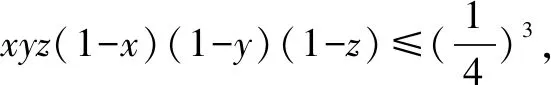
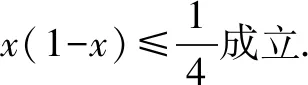
綜上所述，在某些具有對稱性的代數問題中，巧妙地運用對稱性，把握對稱的特質，往往能夠使得問題求解過程變得簡潔明了，實現解決問題方法與思路的優化.