深度思維，讓學習真正發生

王智海

小學數學學習的過程首先是思維的過程，幫助學生學會思維是數學教學的基本目標，促進學生思維發展是數學核心素養最為基本的含義。“長時間思考”的深度思維活動會讓學生想得更清晰、更深入、更全面、更合理。數學活動中，我們需提升學生的思維質量，引導學生深度思維，讓學習真正發生。

一、讓活動更具“情境性”

教學中，教師通過創設情境，調動學生探究的積極性和主動性，激活學生思維。創設情境時，我們需要更多地關注學生原有的認知基礎，而不是僅僅滿足于學生產生“強烈的求知欲望”。我們需要情境更多地為學生學習提供“生動具體”的探究素材，讓情境成為學生的思維的“載體”。

學生在解決稍復雜的實際問題時，需要借助直觀的素材來輔助思維。例如：“小猴幫媽媽摘桃，第一天摘了30個，以后每天都比前一天多摘5個。第五天摘了多少個？”

學生通過獨立思考，用不同的策略來解決這個問題。

第一種，列表格：

第二種：第二天 30+5=35（個） 第三天 35+5=40（個）第四天 40+5=45（個） 第五天 45+5=50（個）

第三種：30+4×5=50（個）。

對于前兩種解題思路，學生容易理解，但對于第三種思維過程，很多學生不是很能理解。于是，請學生上臺介紹了思考過程，仍有很多孩子不理解第五天增加了4個“5”，這時候，我引導學生觀察表格來分析“以后每天都比前一天多摘5個”增加的次數。這樣借助具體的“情景”更深入地思考，從而掌握更為抽象的策略。

感知認識是學生理解知識的基礎，直觀是數學抽象思維的途徑和信息來源。我們在教學時要注意由直觀到抽象，逐步培養學生的抽象思維的能力。

二、讓問題更具“引領性”

我們的課堂教學中，喜歡讓孩子“滿負荷”地學習，所涉及的教學內容太多，承載的任務過重。教學中每一個小知識點都不放過，“碎片化”的教學方式讓孩子疲于應付，而教學活動中，學生的思維能力、學習能力沒有得到充分的發展。如果教學中讓孩子聚焦在幾個核心問題上進行深入的探究、思考，學生的深度思維將得到發展，學習能力也將不斷提升。

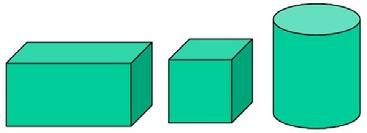
在復習立體圖形的表面積和體積時，首先出示：

通常教師會讓學生一步一步地回顧立體圖形的特征、表面積和體積的計算方法，最后在實際運用中鞏固。而我們設計三個引領性的問題，幫助學生構建更為緊密的知識結構：（1）觀察思考，哪個立體圖形體積計算方法是其他立體圖形計算的基礎？（2）為什么這三個立體圖形的體積計算都可以用“底面積×高”來計算？（3）它們的表面積又有什么聯系？學生圍繞三個問題聚焦在立體圖形體積和表面積計算方法的共性上，這樣學生在構建知識體系時將減少過多的枝節末梢，使自己的思維更為清晰、更為全面。

在教學過程中，教師應根據教材重點和學生的實際提出深淺適度、具有思考性的問題，這樣就將每位學生的思維活動都激活起來，通過正確的思維方法掌握知識。

三、讓氛圍更具“靜思性”

我們的課堂教學一直提倡創設生動有趣的生活情境，營造輕松、歡快的學習氛圍，顯現出孩子在熱鬧的氛圍中“樂學”的景象。而這種“娛樂化”的教學活動中，學生思維的質量卻很難有機會得到全面的發展。我們提倡“靜思性”的氛圍，并不是因靜而冷卻了學生學習的熱情，因靜沖淡了學生的求知欲望，因靜影響了學生的注意力和學習成效，而是讓學生思維專注，進入一種心無旁騖的境界。學生在潛心沉思時需要適合的外部環境，只有足夠安靜的時間和空間才有利于學生思緒飛揚，讓他們的思考不被打擾，更有序、更深入。

我們在課堂上時常過多地突出了“即興思維”能力的培養。教師剛說出口的問題，就希望立刻有孩子能夠舉手回答，希望他能完整、清晰地表述出思路，然后其他同學也能按照這條“最佳路徑”順利解決問題。“看誰先想出解決問題的方法？”“看誰做得又對又快！”教師在學生思考時更多地關注了思維的靈敏性和速度，學生在老師的催促下，往往追尋最終的結果，淡化問題的分析，思考問題的廣度和深度往往不夠，更別提求異思維的發展。同時，學生思維能力的差異很大，很多孩子的思維特性也不同，當沒有給予學生充足的思考時間和空間時，難免影響思維的質量。在教師的“鼓勵”（實質是變相催促）下，學生所受到的思維壓力越來越大，當其他學生說出合理的解決問題的方法時，自我的挫敗體驗必將影響以后思維的積極性。我們在教學中要重視引導學生更細致、更深入地思考，逐漸學會合理、有序地思維。當學生思考中猶豫不決、不得其解時，我們是不是再耐心地等待一會兒，多一些鼓勵的眼神；當孩子急于表述想法時，是不是讓他再想一想，想好了再說；當學生的思維出現誤差時，是不是能引導他自覺反思，有重新思考、表達的機會。

四、讓思維更具“可視性”

思維是一個人獨特的、個體的頭腦中的活動。我們如何讓它變得可以看見呢？我們可以運用一系列的圖式技術把本來不可視的思維，比如說思考的方法、思考的路徑呈現出來，使其變得清晰可見。

通過圖示把零散的知識、概念等看著沒有直接關聯的或者散落的知識梳理在一個系統之中，形成一個復合型的概念網絡。把所學的知識按照其相互作用、相互聯系的方式和秩序組合起來，使知識由繁雜變成簡化概括，使學生對知識的體系和結構產生形象化的感覺和認識。

在“數的認識”的知識整理與復習時，首先我讓學生舉例說說：“怎樣的數是整數？怎樣的數是負數？怎樣的數是小數？”讓學生更清晰地認識數的概念，繼而，我出示了數軸圖來幫助學生理解它們之間的聯系和區別。最后，引導學生討論交流，自主形成了更為清晰的網絡圖。

我們教給學生的知識必定是破碎的，破碎的知識是沒有力量的，破碎的知識也是沒有價值的，要想讓我們的知識真正有力量，產生價值，就必須讓知識結構化。