對曲面光束與弧狀光譜的探究

(1. 山東省高密市豪邁中學，山東 濰坊 261500；2. 南京師范大學附屬中學，江蘇 南京 210000；3. 山東省膠州市第八中學，山東 青島 266300)

三棱鏡折射得到的帶狀光譜，實際上是折射光束在某平面上的投影，若要使這個投影帶有弧度，那么必須想辦法得到曲面光束，下面的方法可以得到曲面光束。

如圖1所示，讓激光筆發出的光束，經細玻璃柱折射后可得到一束平面發散光束，其平面截痕是一條直線段。將該平面光束平行于三棱鏡的棱邊投射到其上，經折射后將形成曲面光束，其平面截痕是一段弧線(如圖2)，每一條發散光線對應的主截面方向不同，各主截面的頂角和各條光線的入射角也不同，故其折射情況也必然不同，這樣，平面光束就變成了曲面光束，引起這種折射現象的主要因素應該是平面發散光束的張角。

圖1

圖2

1 曲面光束的截痕方程

如圖3所示，取過光源點垂直于入射面的直線為z方向，以△OP′Q的頂點O為原點建立坐標系，其中三棱鏡邊長為a，光源到入射點的水平距離為b，垂直距離為d。

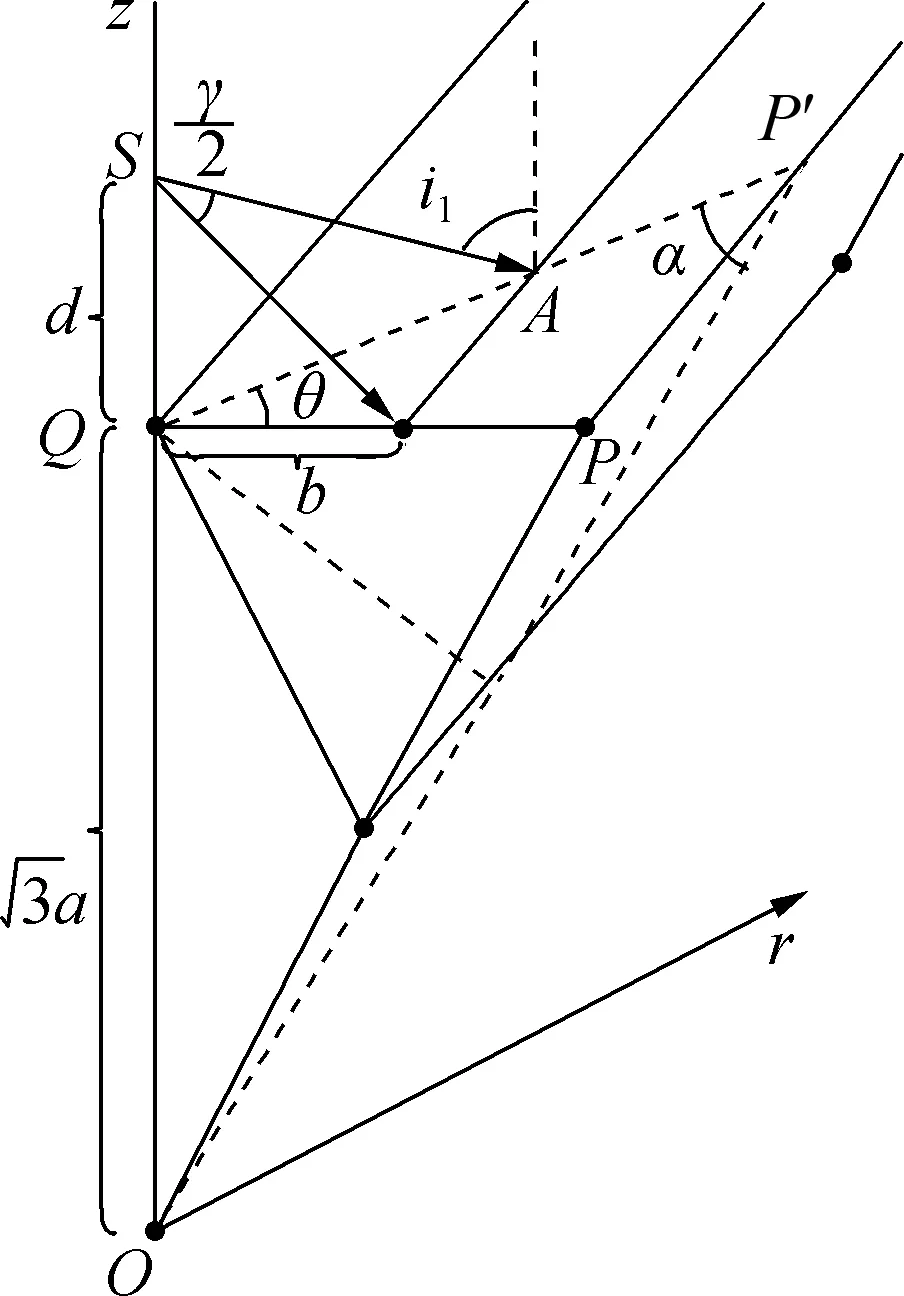
圖3

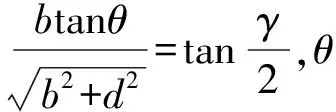
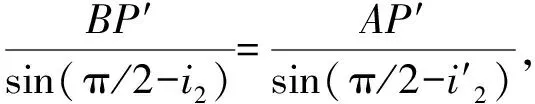
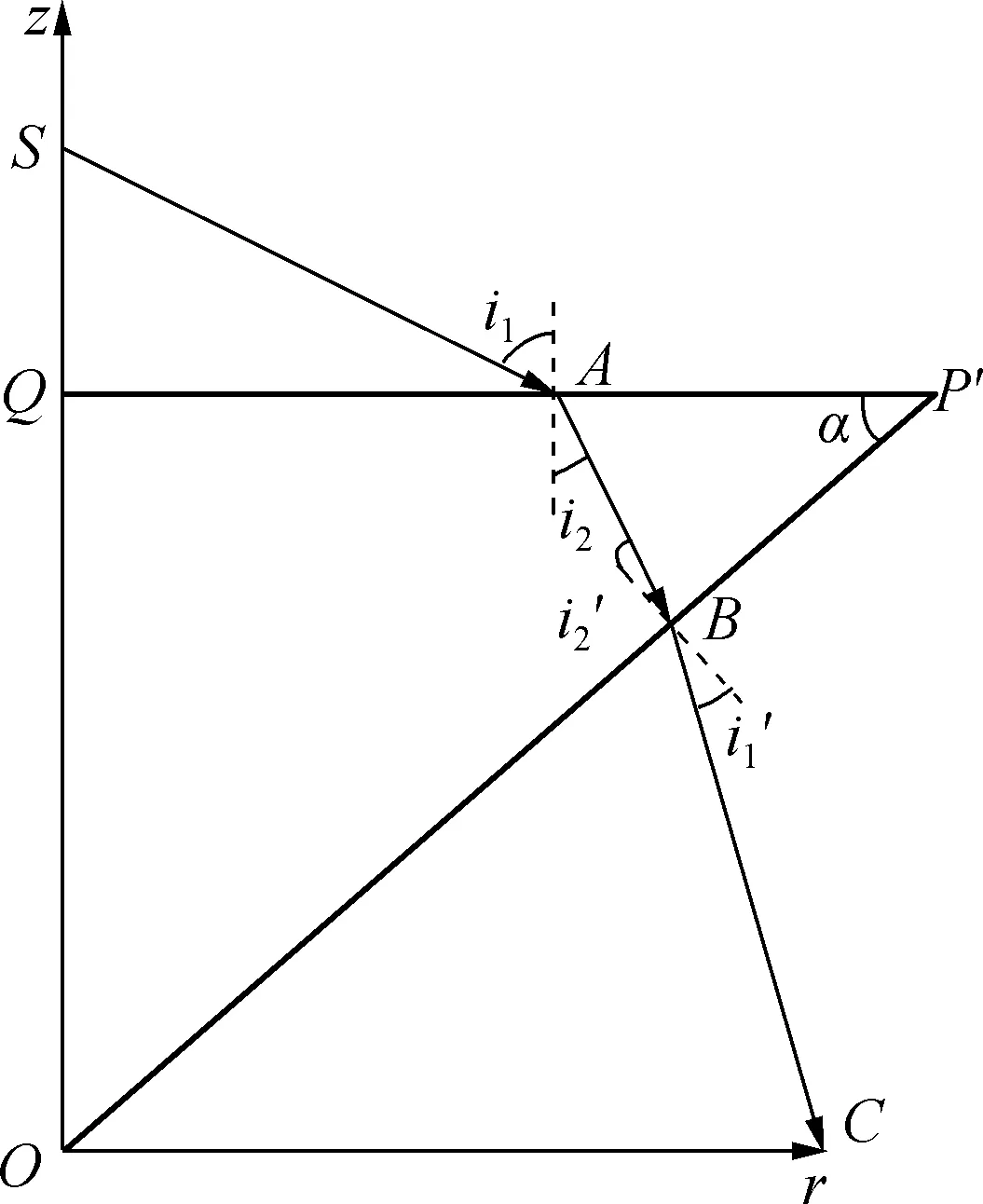
圖4

2 截痕方程的圖像與弧狀光譜

曲面光束的截痕方程中包含的參數有：三棱鏡邊長a、棱鏡的折射率n、光源點到入射點的垂直距離d和光源點到入射點的水平距離b。

首先給參量賦值，令a=3，b=1，d=1，n=1.5，利用Mathematics繪出z=0平面上截痕圖像(如圖5)，比較相同參數值下的實際截痕(如圖6)，可以看出光束截痕的兩端明顯與圖像有差異。

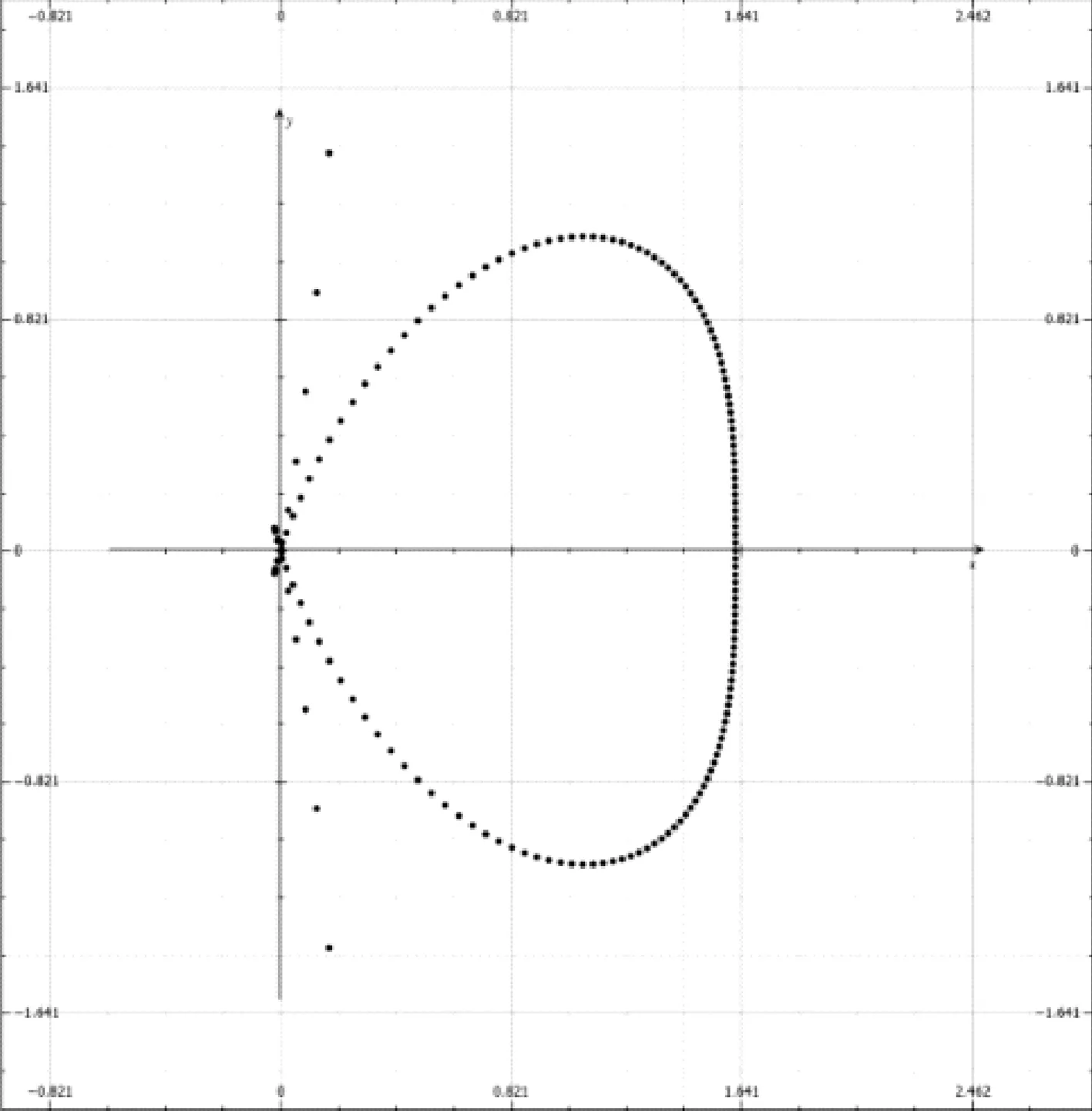
圖5

圖6

究其原因，變量角θ的范圍受光束張角γ的制約，達不到(-90°，90°)，實測可得發散光束的張角γ=90°，易得在b=d=1時，θmax≈45°。取變量角θ=(-45°，45°)繪得圖像(如圖7)，與實驗現象吻合。

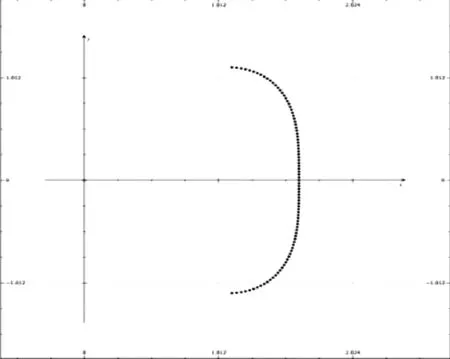
圖7

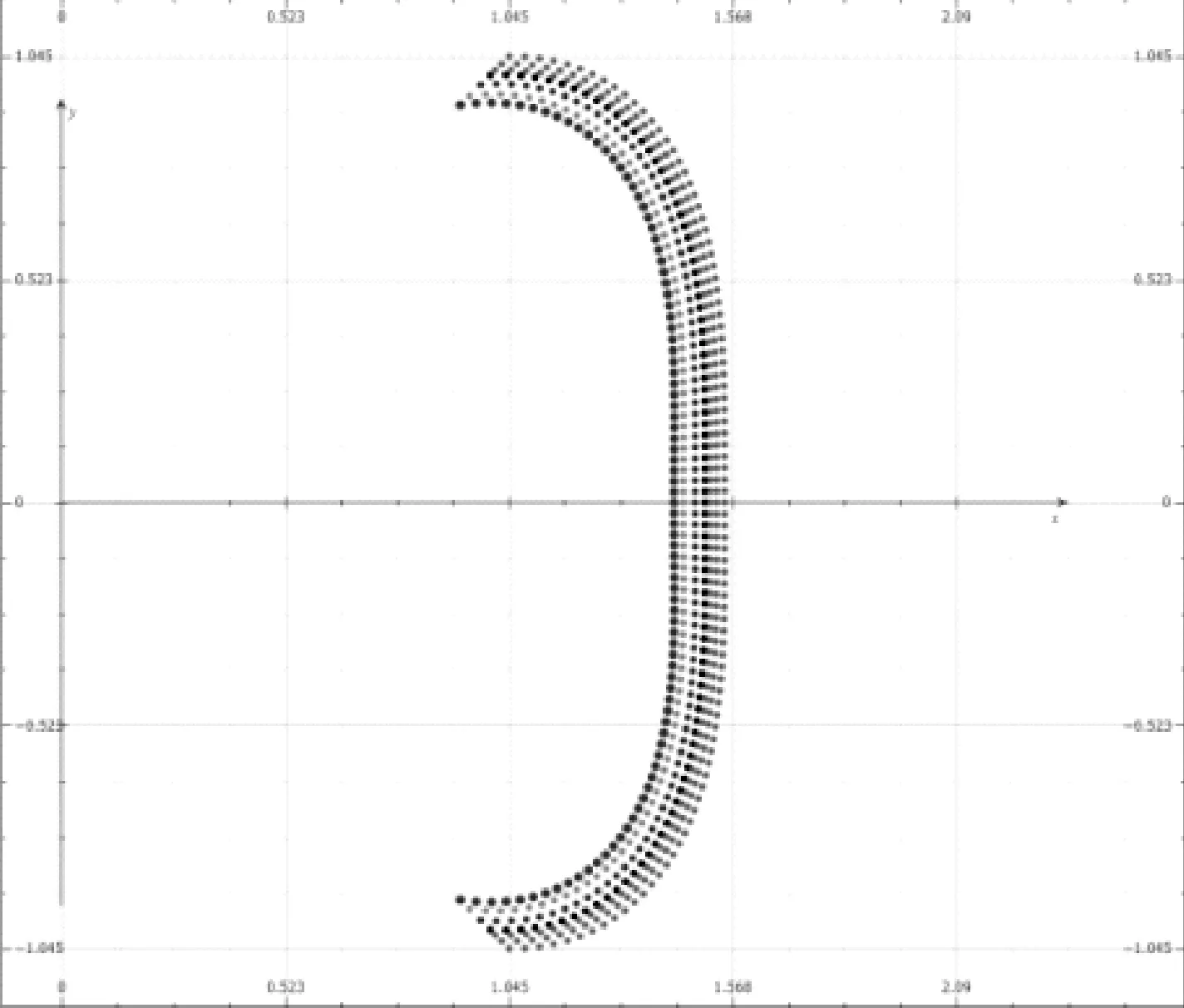
圖8

以上分析都是以紅光的折射實驗為基礎，而各種單色光的折射率不同，會引起色散現象。折射率對應截痕方程中的參數n，冕牌玻璃對各種單色光的折射率見表1。其他參量不變，n依次取表1中數據，可繪出如圖8所示的圖像，是一弧狀光譜。如何從實驗上得到此弧狀光譜呢？根據前述模型，可利用手機上的閃光燈作為白光光源，但其發出的光束是圓錐光束，只需稍加改造即可得到近似的平面發散光束，方法是用黑色絕緣膠布遮住閃光燈的上半部和下半部，只留中間一條縫隙，由縫隙發出的光束即可視為平面發散光束。用手機和三棱鏡做出的弧狀光譜效果如圖9所示，若想得到更強的演示效果，可使用強光手電。

圖9

顏色紅橙紅黃綠青綠青藍折射率1.511041.513891.516301.518291.521951.526261.52982