應用于GNSS射頻芯片的小數分頻電路設計

楊 毅，黃海生，李 鑫，董明月

0 引言

全球衛星導航系統（global navigation satellite system，GNSS）接收機中射頻芯片接收到的信號需要經過濾波放大和下變頻。電路中下變頻就是在本地產生 1個特定頻率的正弦信號與輸入信號相乘，然后濾除掉高頻分量，保留中頻分量[1]。本地正弦信號是由本地的晶振產生的時鐘信號，經過倍頻，然后經過小數分頻，得到1個特定的時鐘信號。由于本地晶振頻率不同，需設置不同的小數分頻器、不同頻率的晶振，得到的目標頻率雖然相同，但是會產生不同的雜散[2]。所以，本文研究設計利用Sigma-delta調制器的特性，使芯片在任何情況下都擁有較低的相位雜散[3]，并針對調制器輸出序列周期太短導致的結構寄生問題，在調制器輸入端加入1個變形m序列進行改善，具體電路采用Verilog HDL實現，設計出1種應用于GNSS射頻芯片的小數分頻電路。

1 小數分頻器原理

1.1 鎖相環頻率合成器原理

射頻芯片采用鎖相環頻率合成器產生本地正弦信號，其工作方式為：鑒頻鑒相器（phase frequency detector，PFD）對內部分頻結果 Fdiv與外部晶振信號Fref進行對比產生脈沖信號[4]，作用于電荷泵（charge pump，CP）控制環路濾波器（loop filter，LPF）輸出電壓 VL的值，VL控制壓控振蕩器（voltage controlled oscillator，VCO）產生信號Fpll[5]，Fpll經過分頻器產生頻率 Fdiv，使得 Fdiv朝著更加接近Fref的方向變化；當 Fdiv與Fref同頻同相，CP的輸出電壓穩定后，VCO產生穩定的頻率使鎖相環鎖定[5]。總框圖如圖1所示。

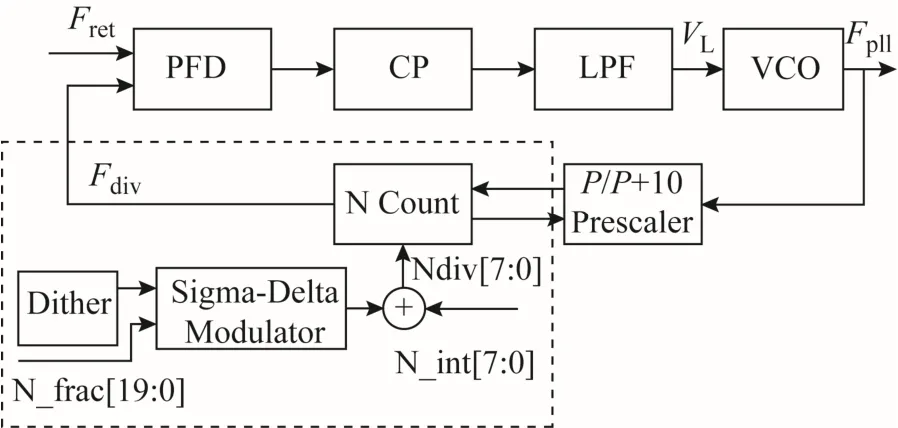
圖1 鎖相環頻率合成器總框圖

圖1 中，虛線框所示為Verilog HDL設計實現的 N.F小數分頻器，由 N count分頻計數電路、Sigma-delta調制器電路以及Dither抖動電路構成，圖中 N_frac與 N_int分別為輸入的分頻比的小數與整數部分，Ndiv為電路內部產生的瞬時分頻比，P/P+1 Prescaler為前置雙模預分頻器。

1.2 小數分頻器電路實現

數字電路進行小數分頻時，每1個瞬時進行的是整數分頻，然后在 1個周期內得到統計意義上的小數分頻結果[6]。

N count分頻計數電路設計如圖2所示。圖2中Input Reg為輸入信號寄存器，aclk為中間控制信號，Mod為預分頻器控制信號。在N count電路得到 1個來自調制器的 8位分頻比 Ndiv[7:0]后，將M與A計數器置數。將Ndiv [2:0]輸入到A計數器中，Ndiv [7:3]輸入到M計數器中，并將Mod信號置1，使得前置分頻器按P+1分頻模式工作，M與A計數器同時對預分頻器輸出頻率開始計數。由于M計數器量程k大于A計數器量程s，所以A計數器先計滿s個脈沖，通過滿量程識別電路將Mod信號置為0，使前置分頻器進行P分頻，當M計到滿量程狀態，即再計（k-s）個脈沖，aclk置 1，電路對下1個分頻比開始計數。

于是在1個分頻周期中，共計s次P+1分頻，計（k-s）次的P分頻，所以1次分頻中的分頻比Ndiv為

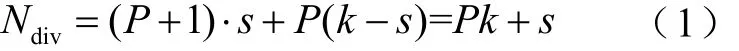
設計采用8/9分頻器，所以在1個周期中得到的分頻比為Ndiv=8k+s。M計數器取值為2~31，A計數器的取值為0~7，由此算得電路輸入分頻比范圍為：16（2×8）~255（31×8+7），由于工作頻率過高，預分頻電路由CMOS全定制搭建[5]。

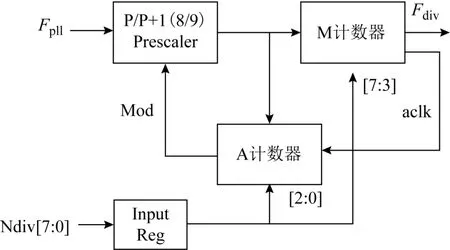
圖2 N count分頻計數電路

2 Sigma-delta調制器電路

2.1 小數雜散產生原因

電路在進行P或P+1分頻時，Fdiv與Fref的相位差會導致 PFD的輸出形成相位累加或遞減[7]，會使得 VCO的控制電壓存在 1個重復性的紋波，當這一紋波作用于VCO時，將產生在載波附近偏移倍數諧波頻點上的邊帶，這些邊帶被稱為小數雜散[8]。這些邊帶將對射頻系統產生嚴重影響，所以需要對小數雜散進行調制處理。

2.2 MASH1-1-1 Sigma-delta 調制器

Sigma-delta調制器用于消除小數雜散已有廣泛研究[1]，MASH型調制器就是用多個1階Sigmadelta調制器進行級聯[9]，相對于只使用1階調制器的小數分頻電路，MASH結構調制器對小數雜散有更好的抑制作用[10]。考慮電路穩定性以及過高的電路復雜度帶來的設計以及功耗問題等因素，設計采用3個1階Sigma-delta調制器級聯的結構，即為MASH1-1-1結構，其z域模型如圖3所示。

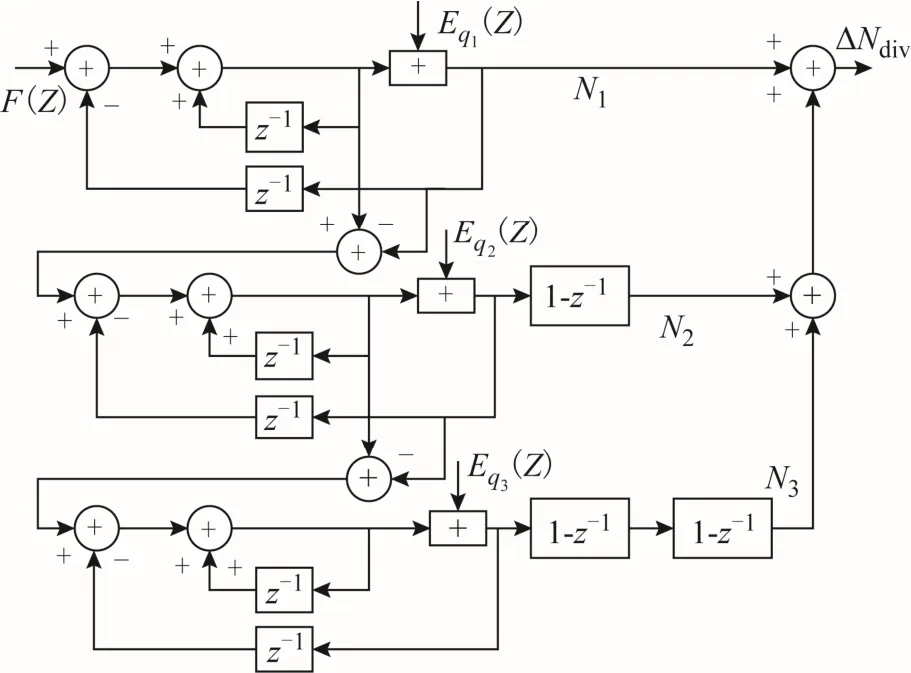
圖 3 MASH1-1-1 Sigma-delta調制器

其傳輸函數為

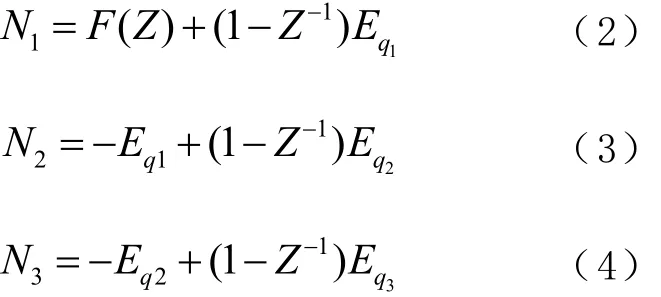
式中：N1~N3為每級調制器的輸出結果； Eq1~Eq3為每級輸入的量化噪聲，級聯后可得

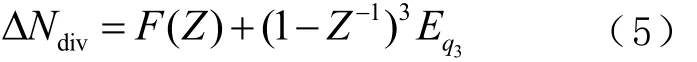
式中△Ndiv為調制器產生的調制序列。式（5）表明：向MASH1-1-1調制器輸入數值F(Z)后，經過多個參考周期平均后，得到結果F(Z)+Q；Q是整個MASH結構輸出量化誤差總值，由于成型后的量化誤差大部分處于高頻處，從而在其作用于VCO之前被低通濾波器濾除；MASH1-1-1 Sigmadelta調制技術從根本上消除了小數分頻帶來的小數雜散。

2.3 MASH1-1-1調制電路設計與實現

圖 4所示為 MASH1-1-1型調制器電路結構，設計采用3個21 bit流水線加法器Add和20 bit寄存器 Reg實現累加以及量化功能，輸入的小數部分為20 bit，每次在小數部分輸入后，將其在最高位接 0拼接成 1個 21 bit的數據后送入第 1級加法器中，調制器開始工作。

圖4中虛線框是噪聲整形電路，3個加法器每個時鐘周期輸出的第 21位作為加法器的進位輸出，相當于量化器的輸出結果，3個進位值（q1~q3）控制噪聲整形電路，產生-3~4的調制序列[3]，輸入的整數部分（N_int）與產生的調制序列求和得到8 bit的分頻比（Ndiv），輸入到 N count分頻計數電路中產生分頻結果Fdiv。

3 調制器結構寄生及其解決方案

3.1 調制器結構寄生產生原因

電路工作時輸入的小數值（.F）需根據加法器位數b用公式：.F=N_frac/2b將其擴展為b位的2進制數，對于第1級加法器輸出結果，若N_frac為奇數，則其輸出序列周期T=2b；若N_frac為偶數，先算得N_frac與2b的最大公約數2n，則第1級加法器的輸出序列周期為T=2(b-n)；

第2級、第3極的加法器輸出周期為第1級加法器輸出周期的 2倍，最終調制器輸出的調制序列周期為第3級加法器的輸出周期2T[7]。

分析可得，N_frac是奇數時，MASH 1-1-1結構調制器的輸出結果可以呈現出極長的周期，但對于輸入數值 N_frac為偶數的部分數值，例如：預期的小數為 0.5、0.25、0.75等時，調制器輸出序列存在周期極短的情況，由此形成了MASH型調制器固有的雜散譜，稱為結構寄生，若不進行處理，則會使小數分頻器的輸出產生大量雜散，影響整個電路的性能。

3.2 調制器結構寄生解決方案

為了解決調制器結構寄生問題，需要打破調制器輸出序列的固有周期，于是在調制器的輸入部分加入了1個產生偽隨機序列的抖動電路，以1階 Sigma-delta調制器數學模型為例，如圖 5所示。

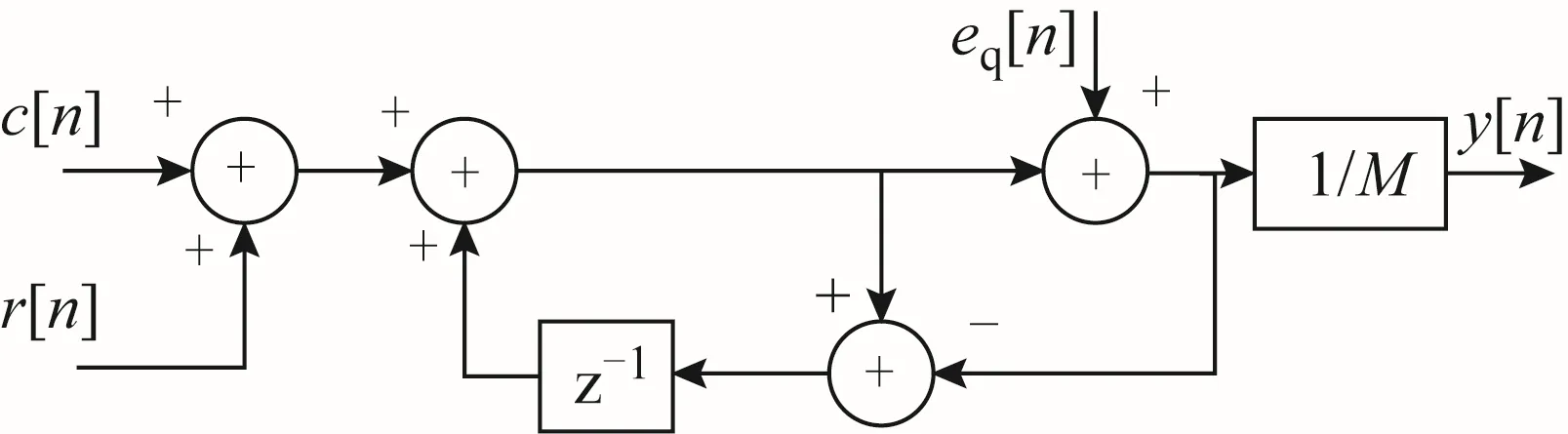
圖5 1階調制器數學模型

根據圖5所示數學模型可得，輸出序列y[n]為

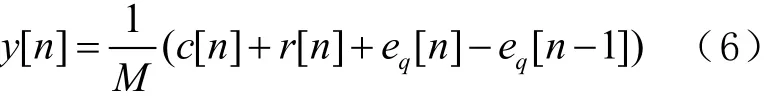
式中：輸入信號 c[n]=Ma，a是預期的小數，M=2b，b為加法器位數；r[n]為注入的偽隨機序列；eq[n]為輸入的量化噪聲。對y[n]在輸出周期N內求和可得

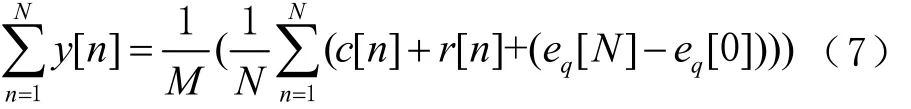
因為量化噪聲具有白噪聲的性質[6]，所以eq[N]= eq[0]，可得

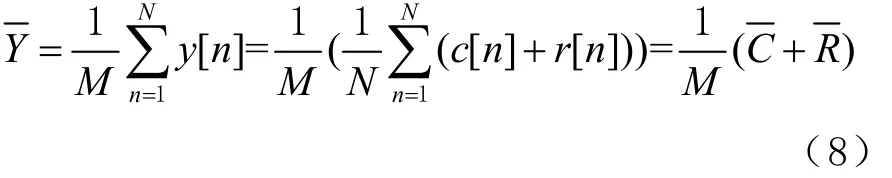
式中Rˉ是隨機序列在周期N內的平均值。若Rˉ=0，則式（8）可化簡得

由式（9）可得，輸出序列y[n]的平均值取決于輸入序列 c[n]的平均值，等于預期的小數值，所以加入1個周期N內平均值為0的偽隨機序列并不改變調制器輸出結果的均值，只會改變輸出結果的周期長度，能有效抑制調制器的結構寄生。

3.3 Dither抖動電路實現

m序列作為1種典型的偽隨機序列，易用數字電路實現，所以設計采用m序列來實現抖動電路。

由于m序列的輸出為0和1，不能直接使用，所以將輸出轉化為-1和1，但個數相差為1，隨機序列的均值不為0，加入調制器會使輸出均值不等于輸入均值，但當輸出序列周期足夠長時，誤差基本可以忽略。設計最終采用24級的反饋移位寄存器來實現m序列，該序列的特征多項式為

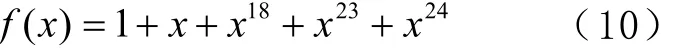
電路結構如圖6所示。

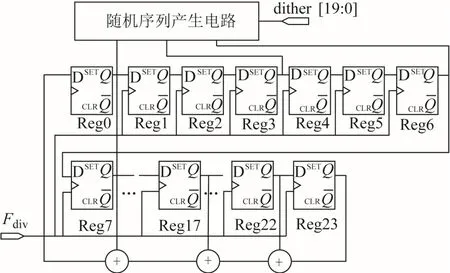
圖 6 Dither抖動電路

由于注入偽隨機序列會產生低頻量化噪聲[11]，但如果進一步打亂偽隨機序列的輸出結果就能有效降低帶來的噪聲，所以在不改變輸出結果周期的前提下對其進行變形：在1個輸出周期內，用3個寄存器的輸出經過 1個隨機序列產生電路來產生（1、0、-1、-2） 4 個數作為抖動電路的輸出（dither）；在每個時鐘周期與輸入的小數部分求和后輸入調制器電路中。

3.4 調制器及抖動電路建模仿真

對加入抖動電路的調制器在 ADS（advanced design system）軟件中建模仿真，當輸入的小數為 0.25時，得到調制器的輸出序列頻譜如圖 7所示。

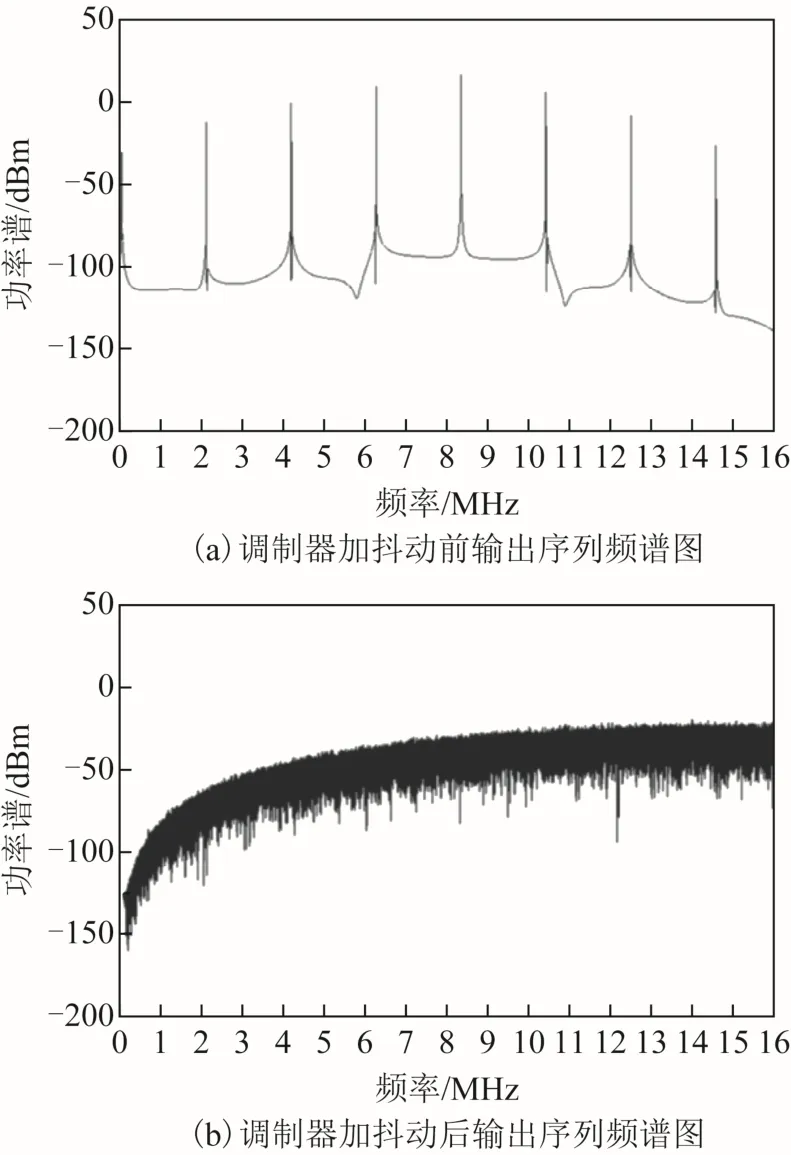
圖7 小數值為0.25時調制器ADS建模仿真結果

圖 7（a）為調制器輸出序列的平均值。由圖 7（a）可以看出，在注入抖動前，調制器的輸出序列頻譜圖中固定頻點的功率譜非常高，輸出序列具有非常明顯的周期性。從圖 7（b）可以看出，注入抖動后，調制器的輸出序列頻譜已經非常平滑，基本沒有毛刺，且加入抖動電路后并未改變輸出序列的平均值，所以，加入抖動電路能在不改變輸出結果的前提下打破調制器的固有周期，從而使其輸出序列的周期變長。

選擇外部輸入晶振頻率 13、16.35、24.55 MHz，中頻頻率 4.092 MHz，在 GPS L1 頻點（1 575.42 MHz）上對調制器在ADS中進行建模仿真，經計算可得預期分頻比分別為：121.500 9、96.606 2、64.338 6（分頻比保留小數點后4位），此時調制器的輸入小數值為奇數。由上文分析可得，調制器的輸出結果本就具有良好的偽隨機性。圖8所示為輸入3個不同小數值后調制器不加抖動與加抖動的輸出序列頻譜圖。

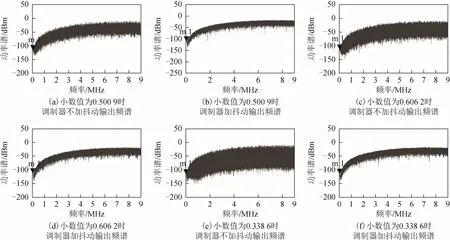
圖8 0.5009/0.6262/0.3386輸入下ADS建模仿真結果

圖8 （a）為調制器輸出序列的平均值，m1為該點處的功率譜，由圖 8（a）、圖 8（c）及圖 8（e）仿真結果可得，注入抖動前的調制器輸出序列雖然不存在固定頻點頻譜能量特別高的情況，但是輸出序列頻譜中仍存在大量的毛刺，這些毛刺作用于射頻芯片時，仍然會對芯片的輸出結果產生很大影響；加入抖動電路后的仿真結果如圖8（b）、圖 8（d）及圖8（f）所示，從仿真結果可以看出，加入抖動后調制器輸出均值并未發生改變，且調制器輸出序列的頻譜非常平滑且基本無毛刺，同時加入抖動后對輸出序列的頻譜有1個非常明顯的整形效果。表1為各個小數值輸入下m1點的功率譜值。

由參考文獻[11]可知：注入1個偽隨機序列會給調制器的輸出序列頻譜增加 1個低頻量化噪聲；但因為設計對偽隨機序列的輸出做了1個變形處理，所以，降低了加入偽隨機序列帶來的低頻量化噪聲的影響。由表1可以看出，m1點的功率譜只惡化了1~3 dBm左右，在環路可接受范圍之內。

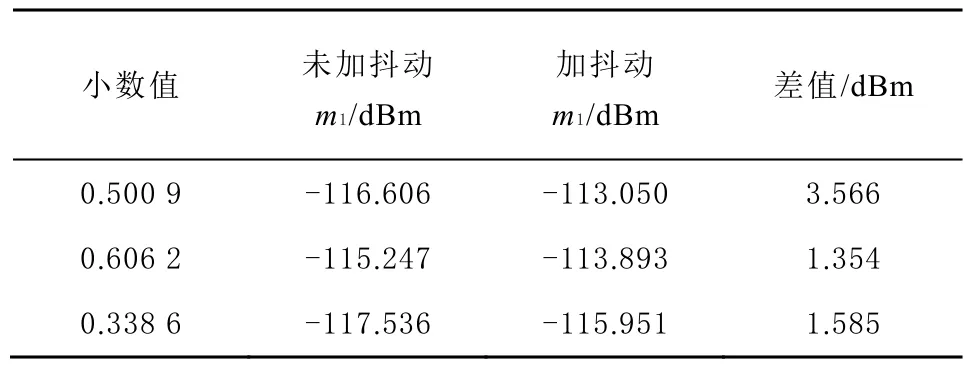
表1 0.5009/0.6262/0.3386輸入下 m1點功率譜

4 電路功能仿真

當分頻比整數部分（N_int）輸入8’h79，小數部分（N_frac）輸入20’h803AF時，目標的分頻比為121.500 9，Modelsim軟件仿真結果如圖9所示，將輸出結果導出并對其求平均值得分頻比為121.500 9，電路功能正確。

圖9 小數分頻電路仿真結果

5 結束語

本文設計了 1種應用于 GNSS射頻芯片的小數分頻電路，能夠實現 16~255之間的小數分頻。仿真結果表明，在保證小數分頻器輸出準確結果的前提下，設計的抖動電路能夠有效抑制調制器本身的結構寄生，且對調制器的輸出頻譜進行了有效整形，對偽隨機序列的輸出處理也有效降低了低頻量化噪聲的影響，可以用于 GNSS射頻芯片中，并能有效改善芯片性能。