由一道高考題引發的思考

內蒙古自治區阿拉善盟第一中學 何春蘭

在利用導數解決函數問題中,我們經常會用到構造函數的思想。構造函數是解決不等式問題的基本方法,根據題目的條件,相應地構造出輔助函數。對于含參不等式就可以通過構造不同變量的函數進行運算，通過進一步研究輔助函數的有關性質,給予巧妙的解答。

本文從一道高考試題出發，追根溯源，研究并尋求更簡捷的運算方法。

這里只研究第（3）問。

我們習慣構造關于自變量是x 的函數,但是像這樣，通過變換自變量,使得構造的函數形式相對簡捷,從而可以簡化運算,達到目的。將此方法可以推廣應用,如下：

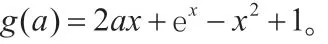
也可以將這個方法應用到2018 年新課標文科（I）卷和（III）中，具體過程如下：

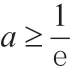
關于2018 年新課標文科（III）卷的過程不再贅述。

波利亞：“觀察可能導致發現，觀察將揭示某種規則、模式或定律。”在教學過程中,根據我們所學習的知識,通過觀察,認識數學的本質特點,靈活運用所學知識和技巧進行求解,從而將抽象復雜的問題轉化為具體簡單的問題,使解題順利完成。我們能從課標出發，處理好高考題，運用好高考題，研發教學資源；結合學生學習的實際做好教學設計，努力創設一種更和諧的學習氛圍，充分發揮學生學習的主動性、積極性，師生之間相互配合，共同完成教學任務，就能使學習目標高質量地完成。