磨損計算模型研究現狀與發展趨勢

趙軍

摘 要：材料磨損失效問題普遍存在，磨損造成的經濟損失巨大，影響國家工業與經濟的發展。磨損計算模型研究有助于預防或控制材料磨損失效，提高機械可靠性，同時對推動摩擦磨損領域的發展有著重大作用。本文對磨損計算模型涉及的材料磨損形式、磨損理論及機理進行分析，并展望了磨損計算模型研究的發展趨勢。

關鍵詞：磨損失效;可靠性;磨損計算模型;磨損理論

中圖分類號：U455.43文獻標識碼：A文章編號：1003-5168（2020）35-0065-03

Abstract： The problem of material wear failure is widespread， and the economic loss caused by wear is huge， which affects the development of national industry and economy. The study of wear calculation model helps prevent or control material wear failure， improve mechanical reliability， and at the same time play a major role in promoting the development of friction and wear. This paper analyzed the material wear form， wear theory and mechanism involved in the wear calculation model， and prospected the development trend of wear calculation model research.

Keywords： wear failure;reliability;wear calculation model;wear theory

在摩擦磨損研究領域中，磨損計算模型的發展比較緩慢。據Meng和Ludema[1]統計，過去40多年所發表的5 466篇文獻中共包含300多個磨損計算模型，且均難以滿足實際應用的要求，其原因并不是缺少對本學科的深入研究，而是由于摩擦磨損研究領域的復雜性和特殊性[2]。從磨損計算模型的發展過程來看，其可以分為三個階段，即早期的經驗磨損計算模型、基于接觸力學機理的磨損計算模型、基于材料失效機理的磨損模型，這些模型大都是基于磨損機理特征而建立起來的，但材料在實際磨損過程中并非只有一種磨損機理起作用，而是多種機理共存，相互作用，并可發生轉化。因此，對于如此錯綜復雜的磨損過程，從單一的磨損機理出發建立磨損計算模型，必然存在不完整性。隨著現代工業的快速發展，磨損計算模型研究的重要性日益突出，工程上迫切地需要建立一套有效的磨損預測方法來對磨損進行定量研究，以便減小或控制材料的磨損，提高機械可靠性。

近年來，計算機技術、材料學及物理化學等相關學科的發展為磨損計算模型的研究創造了更多的條件，其中以計算機為基礎的研究方法得到迅速發展和廣泛應用。本文從磨損機理出發對磨損計算模型的建立過程進行分析，并對未來磨損計算模型研究的發展趨勢提出了看法。

1 磨損理論的研究與發展

弄清磨損理論和表層材料破壞機理是磨損計算模型建立的基礎。按照當今的磨損機理，磨損可以分為磨粒磨損、黏著磨損、疲勞磨損、剝層磨損、能量磨損和腐蝕磨損等。在實際生產中，人們要根據這些磨損形式選用相應的磨損計算模型，對機械零件進行磨損的計算與分析。以下是磨損理論研究過程中建立的幾種典型磨損理論，為磨損的理論研究奠定了基礎。

1.1 磨粒磨損理論

磨粒磨損主要是磨粒的犁溝作用和微觀切削作用，磨粒磨損過程中有尖銳棱角的硬質磨粒被壓入摩擦表面，兩摩擦表面有相對運動時，該磨粒就像刀具一樣對材料表面產生微觀切削作用[3]。

1.2 黏著磨損理論

黏著理論認為，摩擦表面的接觸實際上是表面上微凸峰間的接觸，接觸面積小，峰點處于塑性狀態，摩擦過程中的瞬時高溫使兩表面凸峰形成黏結點，滑動過程中黏著點不斷地斷開和焊接，最終由凸峰接觸的黏著效應導致黏著磨損。

1.3 疲勞磨損理論

疲勞磨損理論認為，表面粗糙度和波紋度的存在使摩擦副表面的接觸不是連續的，摩擦過程中表面受到周期載荷作用，當應力循環次數達到一定值時，表面就產生疲勞破壞，即疲勞磨損[4]。

1.4 腐蝕磨損理論

簡單地說，腐蝕磨損就是金屬與環境介質發生化學反應，腐蝕和磨損的交互作用是腐蝕磨損過程中的普遍現象，是機械和腐蝕共同作用的結果。

1.5 剝層磨損理論

摩擦時，硬表面粗糙峰相對軟表面滑動，使軟表面受到循環載荷的作用，表層內產生剪切塑性變形，形成周期性位錯;當剪切變形積累到一定程度時，表層開始出現位錯堆積，導致裂紋或空穴的形成，當裂紋長度達到臨界值后，就以片狀磨削形式脫落[5]。

1.6 能量磨損理論

摩擦過程中，大部分的能量以摩擦熱的形式耗散掉，但有9%～16%的能量以勢能的形式存儲在摩擦副表層材料中，當能量累積到臨界值時，材料就會發生塑性流動或形成裂紋，最終脫落，導致材料的磨損。

2 常見磨損計算模型的建立與分類

2.1 磨粒磨損模型

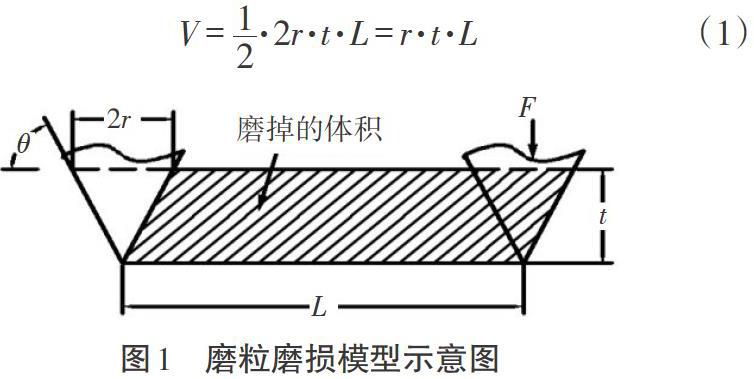
迄今為止，人們已建立了許多磨粒磨損模型，其中以拉賓諾維奇（Rabinowicz）建立的模型為代表，在相關領域得到較多應用。磨粒磨損模型如圖1所示，拉賓諾維奇根據磨粒磨損的微切削機理導出磨粒磨損公式。其中，[L]為滑動距離;[F]為磨粒所受載荷;[t]為磨粒壓入磨損材料的深度;[θ]為磨粒與磨損面的夾角;[r]為圓錐體磨粒的半徑。磨損體積為：

磨粒壓入深度[t=r·tanθ]，材料硬度與所受載荷的關系[πr2=FH]，代入式（1），得Rabinowicz方程：

拉賓諾維奇模型的主要不足之處如下：假設所有的磨粒都參加切削，溝內所有的材料都被磨掉，實際上，只有少數磨粒參加切削，溝內也只有部分材料被磨掉;[K]值只考慮了磨粒的形狀，而沒考慮磨粒大小、硬度等因素的影響;只考慮了材料硬度因素，而沒考慮材料其他性能的影響。

2.2 黏著磨損模型

黏著磨損一直作為一種重要的磨損類型，國內外的專家、學者做了大量研究，其中以Archard模型為代表。

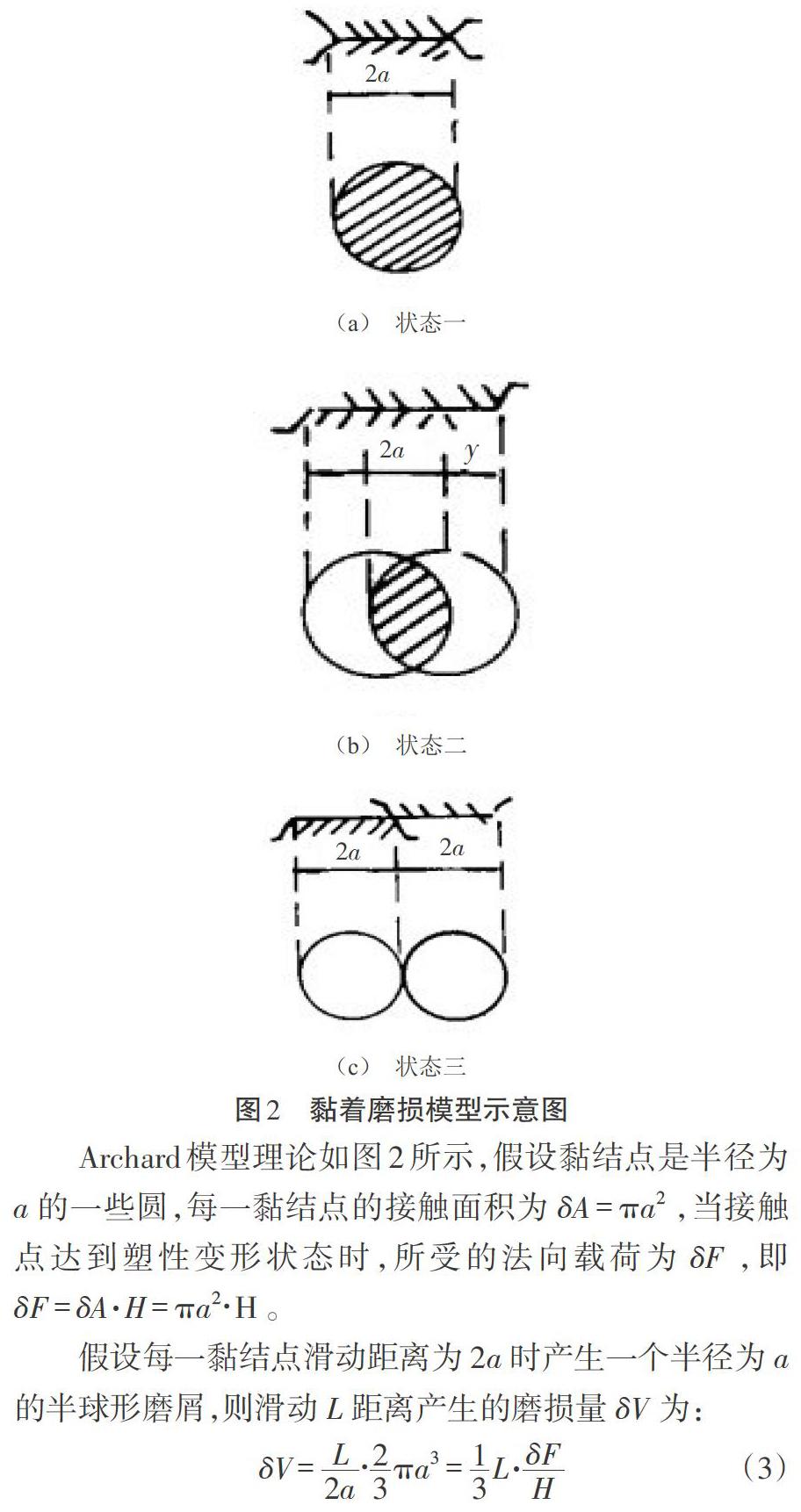
Archard模型理論如圖2所示，假設黏結點是半徑為[a]的一些圓，每一黏結點的接觸面積為[δA=πa2]，當接觸點達到塑性變形狀態時，所受的法向載荷為[δF]，即[δF=δA·H=πa2?H]。

假設每一黏結點滑動距離為[2a]時產生一個半徑為[a]的半球形磨屑，則滑動[L]距離產生的磨損量[δV]為：

滑動過程中總的磨損量[V=δV]，即

Archard模型的不足之處如下：只考慮了材料硬度，而沒有考慮材料的其他特性;磨損模型是在一定假設基礎上導出的，與實情況不符;不能普遍適用。當磨損的條件發生變化時，該模型就不再適用;磨損系數[K]的確定困難。

盡管Archard模型存在很多不足之處，但仍被認為是磨損研究領域中經典的公式之一，廣泛應用。

2.3 疲勞磨損模型

塑性接觸情況下的疲勞磨損計算公式如下：

式中，[C]為表征微凸體形狀和材料強化的系數（無量綱）;[pa]為名義壓力;[t]和[e0]為摩擦疲勞曲線參數;[β=1/（2V+1）]，[V]為支承面曲線的冪近似函數;[Δ]為表面粗糙度參數，[Δ=Rmax/rb12]，其中[Rmax]為輪廓最大高度，[r]為微凸體頂部的曲經半徑，[b]為支承面曲線參數（無量綱）;[HB]為材料布氏硬度。

式中，[σT]為材料屈服極限;[f]為摩擦系數。

式（5）考慮了表面微觀幾何特性、材料物理、機械性能等，同樣該公式拋開了磨損機理的本質，難以滿足工程實際應用的要求。

2.4 腐蝕磨損模型

腐蝕磨損包括氧化磨損和電化學磨損兩大類[6]，其中以Quinn提出的氧化磨損計算模型最為典型：

式中，[W]為磨損率;[a]為微凸峰接觸平均半徑;[v]為滑動速度;[p]為載荷;[Ac]為阿累尼烏斯常數;[ξ]為氧化膜臨界厚度;[f]為氧化物質量分數;[ρ]為氧化膜密度;[R]為普適氣體常數;[Qp]為氧化反應的活化能;[T]為微凸峰接觸溫度。

上述公式中包含的變量多，計算困難，對實際應用沒有太大意義，但可以用來分析各變量對磨損率的影響。

3 磨損計算模型的應用及發展趨勢

磨損表現出來的統計特性與材料表面性質有著密切的聯系，從數理統計角度研究磨損規律，更符合磨損基本特性。近年來，根據數據統計分析方法建立的磨損計算模型得到了大量應用，在一定程度上滿足了工程應用的需求，但也存在局限性，需要確定自變量、因變量間的關系，需要大量的試驗數據支撐，對數據質量要求也很高，由于磨損的復雜性，有些情況很難直接用函數關系式來描述磨損量。隨著科學技術的發展，人們開始用人工智能的方法建立磨損模型，其能夠反映樣本所蘊含的規律，特別適用于像磨損這樣的變量多、關系復雜或尚不明確的系統[5-7]，但該方法建立的模型沒有直接的數學表達式，不便于研究各個因素與磨損的關系。

疲勞斷裂理論和損傷力學研究的深入以及分子動力學和計算力學的迅速發展為尋求可靠的磨損預測方法和建立精確的磨損模型提供了新的機遇，利用有限元法、分子動力學以及耗散粒子動力學等方法對磨損進行模擬研究是未來磨損研究發展的趨勢。另外，在納米摩擦學的推動下，磨損將進入微尺度研究模式，將在分子、原子的基礎上研究材料的磨損性能，從微觀結構上建立磨損定律和磨損公式。

4 結論

磨損模型的建立是摩擦磨損研究的重要目標之一，良好的磨損模型可對零件的磨損進行有效預測和精確計算，從而提高機器的可靠性和壽命，直接關系到整個工業世界的經濟效益。過去所建立的磨損模型存在很大的缺陷，沒有得到實際應用，隨著現代先進科技的發展以及對磨損本質的深入認識，如今所建立的磨損模型比以往的精確、合理，并在相關領域得到了應用，但這些模型仍存在一定的局限性，還不能完全滿足社會生產的要求。

磨損模型的研究一直以來是磨損研究領域的重點和難點，為此，磨損研究人員必須進行長期的、大量的、系統的研究。鑒于磨損模型研究的重要性和迫切性，本文對磨損計算模型涉及的材料磨損形式、磨損理論及機理進行淺析，并對當前磨損計算模型研究的發展趨勢提出了看法，為進一步建立更全面的磨損理論和精確的磨損模型提供參考。

參考文獻：

[1]Ludema K C.Mechanism-based modeling of friction and wear[J].Wear，1996（200）：1-7.

[2]李娟，夏建中，孫志禮，等.磨損預測模型試驗研究[J].現代制造工程，2011（5）：117-119.

[3]孫偉春.磨粒磨損研究的現狀和發展趨勢[J].技術創新與應用，2008（2）：71-72.

[4]溫詩鑄.材料磨損研究的思考與進展[J].摩擦學報，2008（1）：1-5.

[5]Nam P Suh.An overview of the delamination theory of wear[J].Wear，1996（200）：1-7.

[6]H C Meng，K C Ludema.Wear models and predictive equations：their form and content[J].Wear，1995（181）：443-457.

[7]徐流杰，魏世忠.基于BP神經網絡對的V9-Cr4-Mo3高速鋼冷軋輥磨損模型[J].摩擦學報，2006（6）：541-544.