在變式教學中提升數學思維能力

浙江師范大學物理與電子信息工程學院 孔勝濤 321004

所謂“變式教學”這里是指在數學教學中通過對數學問題多角度、多層次的變換，突出數學問題的本質特征，引導學生從變的現象中發現不變的本質，從不變的本質中探索變的規律，目的在于培養學生靈活多變的數學思維能力.在高中數學解題教學中，如何才能有效提升學生的數學思維能力？這是值得每一位數學教師積極探索的問題.筆者拙見，在高中數學解題教學中，實施變式教學能有效提升學生的數學思維能力.但在實施變式教學時，切忌隨意、盲目地進行變式，要結合教學內容和教學目標，適時適度地進行.下面以一道線性規劃高考題的變式教學為例，介紹在高中數學解題教學中讓學生的數學思維能力因實施“變式教學”而提升的一些思路和方法.

A.-1 B.1 C.10 D.12

解析：作出滿足已知條件的可行域，如圖1所示.

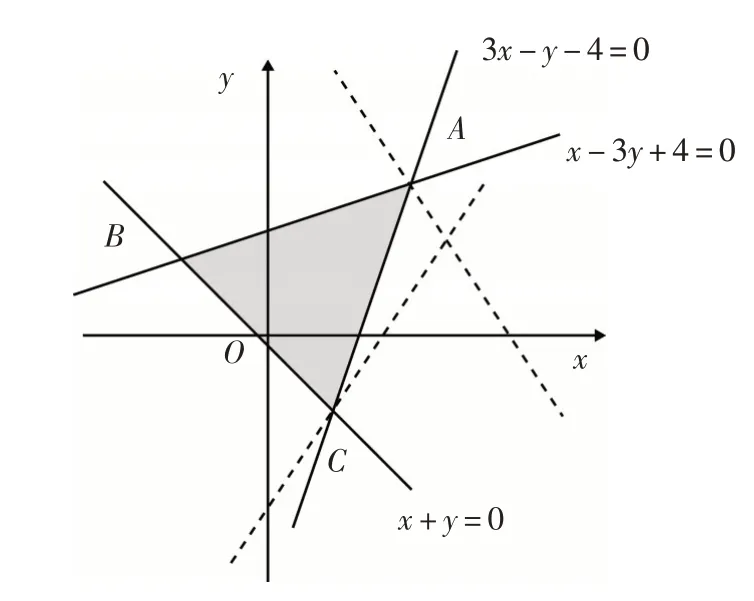
圖1

解法2：（端點代入法）把A(2,2)，B(-1,1)，C(1,-1)代入z=3x+2y，得zmax=10.故選C.

1 改變目標函數

1.1 目標函數為線性目標函數

解析：作出滿足已知條件的可行域，如圖1所示.

解法2：（端點代入法）把A(2,2)，B(-1,1),C(1,-1)代入z=3x-2y，得zmax=5.

評注：對線性目標函數z=ax+by(b≠0)的最值問題，要注意b的正負性對z的影響.

1.2 目標函數為含參線性目標函數

解析：作出滿足已知條件的可行域，如圖1所示.

解法2：（端點代入法）把A(2,2)，B(-1,1),C(1,-1)代入目標函數z=ax+2y，可分別求得a=2，a=-6，a=10.經檢驗a=10不符合題意，所以a=-6或a=2.

解析：作出滿足已知條件的可行域，如圖1所示.

解法1：若a=0，可知不符合題意；若a＜0，由目標函數z=3x+ay得時截距最小，z取得最大值，故8=3-a，解得a=-5；若a＞0，由目標函數z=3x+ay得過A(2,2)時截距最大，z取得最大值，故8=6+2a，解得a=1.綜上所述，a=-5或a=1.

解法2：（端點代入法）把A(2,2)，B(-1,1),C(1,-1)代入目標函數z=3x+ay，可分別求得a=1，a=11，a=-5.經檢驗a=11不符合題意，所以a=-5或a=1.

評注：對線性約束條件下含參線性目標函數最值問題，用端點代入法求解依然成立，但是在求解的過程中要注意代回檢驗.

1.3 目標函數為非線性目標函數

1.3.1 目標函數為曲線型

解析：作出滿足已知條件的可行域，如圖2所示.由目標函數z=x2+y得y=-x2+z，當曲線y=-x2+z與x+y=0相切時，z最小，設切點為D(x0,y0)，則y′|x=x0=-2x0=-1，可求得切點為此時對應的，所以z=x2+y的最小值是

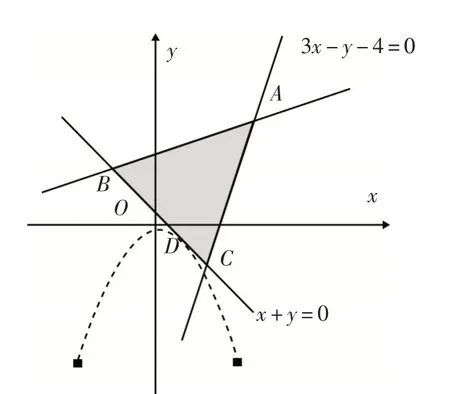
圖2

評注：目標函數為曲線型，它的最值一般是在切點取到，而不是在線段端點，不可盲目使用端點代入法.

1.3.2 目標函數為距離型

解析：作出滿足已知條件的可行域，如圖3所示.

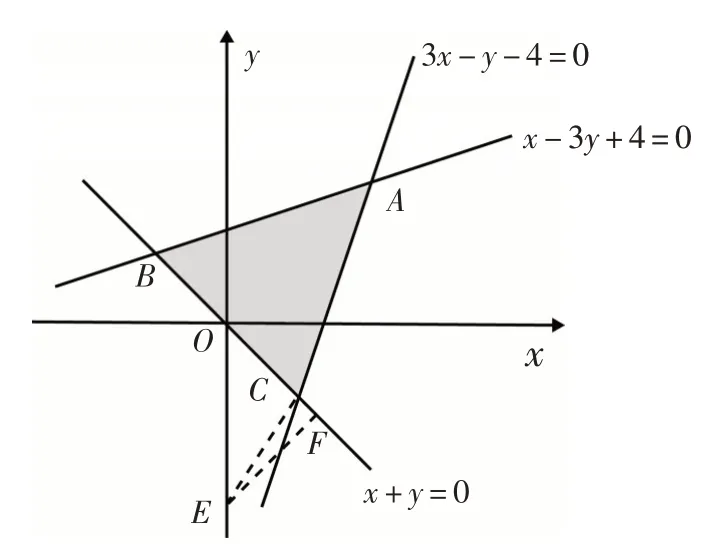
圖3

目標函數x2+(y+3)2表示可行域內部的點M(x,y)到點E(0,-3)的距離，作EF⊥BC于點F，則不在可行域內，結合圖形可得

評注：對于兩點距離型的目標函數，解題時要注意它的最小距離不一定是定點到一條邊界線的距離.

1.3.3 目標函數為斜率型

評注：對于斜率型目標函數的取值范圍，可以將目標函數對應的直線繞定點旋轉，得到斜率的取值范圍.

2 改變約束條件

2.1 可行域為曲線型

解析：作出滿足已知條件的可行域，如圖4所示.由目標函數z=3x+2y得，結合圖形可知：當直線相切時，z最大.設切點D(x0,y0)，則得切點為，對應的.所以z=3x+2y的最大值是

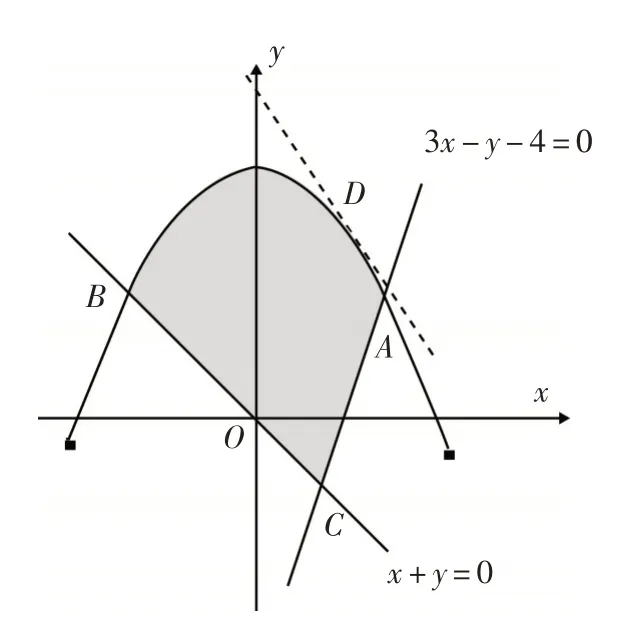
圖4

評注：本題中目標函數z=3x+2y的最大值是在切點D處取得，而不是在端點A，B，C處取得.當可行域邊界有曲線時，要注意目標函數的最值能否在切點取得.

2.2 約束條件含有參數

解析：作出滿足已知條件的可行域，如圖5所示.直線ax-3y+4=0過定點斜率目標函數z=3x+2y的最大值是7，則3x+2y=7必過可行域內的點，求出直線3x+2y=7與3x-y-4=0的交點則直線ax-3y+4=0過，代入求得

評注：對于約束條件含有參數的線性目標函數的最值問題，利用逆向思維求解比較簡便.

3 線性規劃與其它知識交匯

3.1 線性規劃與恒成立交匯問題

解析：作出滿足已知條件的可行域，如圖3所示.可求得A(2,2)，B(-1,1)，C(1,-1)，把A,B,C代入不等式-5≤ax+2y≤8得值范圍是[-3,2].

評注：對于線性約束條件下線性目標函數的最值問題，用端點代入法求解較簡捷.

3.2 線性規劃與不等式交匯問題

評注：本題主要考查了線性規劃和基本不等式的有關知識，考查了數形結合思想、推理論證能力和運算求解能力.

圖6

綜上所述，在高中數學解題教學中實施變式教學，一方面在變中突出不變的解題方法，講一題、通一類、會一片，能有效促進學生對數學技能的掌握，從而提升學生分析問題、解決問題的數學思維能力；另一方面多角度層層遞進的變式問題，符合學生的認知規律，能有效深化學生對數學知識的理解，從而提升學生分析問題、解決問題的數學思維能力.因此，在高中數學解題教學中，實施變式教學能有效提升學生的數學思維能力.