基于譜元法的低頻平面波電磁場數值模擬

萬文武, 李長偉, 熊 彬, 高 磊, 宋衛文

(桂林理工大學 a.地球科學學院; b.廣西隱伏金屬礦產勘查重點實驗室, 廣西 桂林 541006)

0 引 言

在過去的幾十年里, 地球物理電磁法取得了快速發展[1], 出現了大量的研究成果。傳統電磁正演主要包含了積分方程法(IEM)、 有限差分法(FDM)和有限元法(FEM)[2-6]。與FDM和FEM相比較, IEM的效率非常高, 主要是其離散的區域和方程組都非常小, IEM解的精度與對稱矩陣的稠密性息息相關, 難以達到高精度。FDM使用交錯有限差分法離散控制方程, 應用于電磁場中, 計算簡單、 編程容易實現, 被廣泛應用于電磁正演模擬中，其缺點在于無法使用非結構化網格, 難以模擬復雜地質體。FEM具有較好的靈活性, 能夠使用結構化網格和非結構化網格。李長偉等[7]利用仿射坐標變換技術, 應用于平行多面體單元的單元分析, 極大地提高計算效率, 成為有效的電磁正演模擬方法, 特別是在復雜地形的正演研究中。熊彬等[8]借助COMSOL 生成完全非結構化三維網格, 引入Coulomb 規范和適當的邊界條件保證矢量位唯一。在有限元方法中, 為提高求解精度需要對網格加密, 會導致計算量增加；另一種提高精度的策略是提高插值多項式的階數, 即高階有限元法。Schwarzbach等[9]和Grayver等[10]運用高階有限元結合面向目標的局部網格細化, 可以達到較高的正演精度。

譜元法(spectral element method, SEM)最早是Patera在1984年提出的求解流體Navier-Stokes方程的一種數值方法[11]。 近年來, SEM在計算地球物理中得到廣泛應用, 如Seriani等 、 Komatitsch等提出基于Chebyshev和Legendre多項式的譜元法模擬地震波[12-13], 能夠模擬物性不連續介質中的體波和面波的傳播特征。隨著開源包SPECFEM的出現, 在地震研究中SEM成為解決局部和區域問題的一種流行方法[14-16]。如Magnoni等[17]采用了SEM對2009年意大利中部發生的6.3級地震產生的復雜波場進行模擬；王秀明等[18]引入基于預條件下共軛梯度法的元算法；劉有山等[19]和李琳等[20]基于Fekete和Cohen節點實現了譜元法采用三角網格剖分的地震模擬。在地球物理電磁法領域, 一些研究者將SEM應用于航空電磁和可控源電磁法的正演模擬， 如Lee等[21-22]提出了基于Gauss-Lobatto-Legendre(GLL)多項式矢量電磁波方程和三維瞬變電磁問題， Ren等[23]提出了一種新的時間域伽遼金SEM, 減少了未知數個數； Liu等[24]利用高階混合階SEM分析了各向異性和波導, 在邊界上使用了旋度一致的GLL多項式和節點基于GLL的標量基函數來計算正向和切向分量得到場值； Huang等[25]利用基于GLL插值多項式基函數的譜元法實現了頻域航空正演模擬； Zhou等[26]將基于GLL多項式的譜元法應用到井地電磁中解決了低頻電磁場問題； 劉玲等[27]實現了基于GLC插值基函數的譜元法在頻域三維海洋可控源電磁正演模擬研究。

與有限元相似, SEM也是將區域剖分成互不重疊的子單元, 在每個子單元內基于譜方法進行插值。 SEM能夠用結構化或非結構化網格模擬復雜的幾何形狀, 但與傳統的有限元相比, 譜元法具有指數收斂特性。SEM結合了有限元的靈活性和譜方法的高精度, 減少了內存和CPU的需求。為提高大地電磁法正演計算的效率及精度, 本文將高精度的譜元法應用到低頻平面波電磁場數值計算中。 在研究區域使用稀疏網格, 采用GLL多項式構建插值基函數, 利用GLL多項式的完全正交性, 形成對稱的質量矩陣, 減少了計算時間, 并通過高階插值基函數來提高計算精度。與國際標準模型COMMEMI2D-0、 COMMEMI2D-1計算比對, 驗證了本文算法的可行性和有效性, 還設計了幾個含有構造特征的典型地電模型, 分析其大地電磁響應特征, 為實際野外地質工作提供參考。

1 譜元法基礎理論

1.1 控制方程

采用時變因子e-iwt, Maxwell方程可寫為

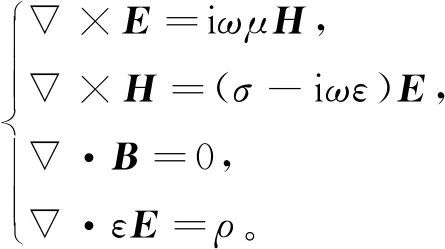
(1)

其中:E為電場強度(V/m)；H為磁場強度(A/m)；B是磁感應強度矢量(T)；ω為角頻率;σ為介質的電導率;ε為介電常數;μ為介質的磁導率;ε、μ分別取真空中的介電常數和介質磁導率, 即ε=ε0=1/36π×10-9(F/m)、μ=μ0=4π×10-7(H/m), 對Maxwell方程組(1)中的第一個方程取旋度, 得到E滿足的矢量Helmholtz方程

(2)

1.2 SEM基函數

采用高斯-洛巴托-勒讓德(Gauss-Lobatto-Legendre)多項式作為插值基函數, 一維參考域的N階GLL插值多項式[21]的表達式

(3)

其中:LN(ξj)為Legendre多項式;ξj為GLL插值節點;j=0, 1,…,N。

對于二維等參單元, 其N階GLL插值基函數為

(4)

(5)

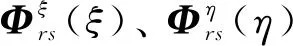
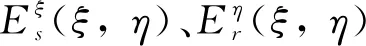
1.3 GLL插值基函數節點和階數的選擇

在SEM中, 選擇基函數和用于物理量插值的配置點是決定SEM法能否成功地關鍵。在標準單元中, 選擇不同函數展開形式對計算效率和數值精度都有很大影響。由于Legendre正交多項式的SEM, 在單元數值積分節點和函數插值節點選擇的是同一點, 在數值計算過程中產生的質量矩陣是對角陣, 具有簡化數值計算和提高計算效率等優點, 從而本文選擇GLL積分。根據劉玲等[27]和Yin等[28]的研究, 當插值階數小于4階時, 必須通過增加單元個數才能保證SEM的高精度求解, 避免數值計算誤差較大問題。理論上, 當多項式插值階數無限增大時, SEM計算的結果越逼近精確解, 但計算機內存和計算時間相應增加。通常采用4～8階多項式插值基函數, 考慮到精度和計算量的平衡, 本文選擇了4階的GLL插值多項式。

提高SEM的精度可以通過網格單元數量和增加每個參考單元的插值節點或提高多項式基函數的階數, 也就是說, 網格大小和插值基函數的階數直接決定了SEM的精度和耗時。在選取網格大小和基函數的階數時, 網格尺寸越小和基函數階數越高, 隨之精度越高, 越接近數值解,但需要計算機的內存越大和計算時間越長。網格剖分在SEM計算中是一個極其關鍵的步驟, 需要不斷重復調試適合的網格單元(包括網格形狀、 網格數量、 網格尺寸)。

1.4 變分方程離散化

將計算區域Ω離散成一組互不重疊的子區域Ωe。對于任意四面體單元Ωe, 利用一個等參變換將其轉換成標準參考單元, 即設物理單元坐標和標準參考單元坐標之間的映射函數為Fe:Λ?Ω, 對剛度矩陣和質量矩陣使用同樣的映射函數轉化到參考域中計算。物理單元與參考單元之間的轉換如圖1所示, 右邊為物理坐標(x,y)下的四邊形單元, 左邊是標準參考(ξ,η)下的四邊形單元,ξ,η∈[-1, 1]。

使用協變量映射[29]表達式計算參考域下基函數

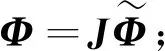
(7)

(8)

(9)

將微分方程(2)轉化為積分問題, 采用伽遼金

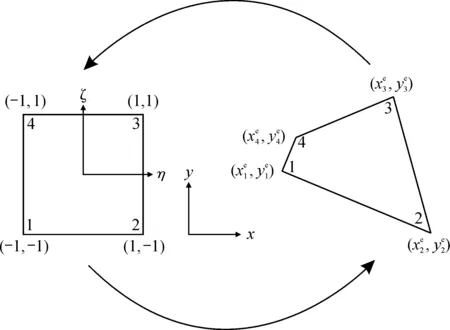
圖1 物理單元與標準參考單元的轉換

加權殘差法, 令加權殘差為0, 即

?Ωevi·(×μ-1(×E)-iω(σ-iωε)E)ds=0,

(10)

其中,vi為加權函數。

基于格林第一定理和狄利克雷邊界條件n×E|?L=0, 把式(10)改寫成

?Ωe(μ-1×Vi)T·(×E)ds-

(11)

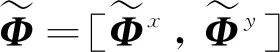
(12)

其中,Na是基函數的個數。對單元進行集成, 得到最終的線性方程組

(A-B)E=0,

(13)

其中:A為剛度矩陣;B為質量矩陣。

(14)

(15)

其中,k是單元總數。對于磁場H計算與上述類似的方法對Maxwell方程組中第二個方程取旋度得到, 使用了穩定雙共軛梯度算法求解上述線性方程組, 可得到電磁場的分布。

2 算例分析

為了驗證算法的正確性和有效性, 本文設計了從簡單到復雜的地電模型進行測試, 采用4階GLL多項式作為插值基函數, 在如下的微型計算機平臺上進行運算:處理器 Intel(R) Core(TM)i5-4210 CPU@1.70 GHz 2.40 GHz, 內存8 GB, Windows 10 64位操作系統。

2.1 算法驗證

算例1采用國際標準模型庫中的COMMEMI 2D-0和COMMEMI 2D-1模型[30]對本文算法進行驗證, 模型如圖2所示。

圖2 模型COMMEMI 2D-0(a)及COMMEMI 2D-1(b)示意圖

在圖2a中，x∈[-50, -10]區域上電阻率為10 Ωm、x∈[-10, 10]區域上電阻率為1 Ωm、x∈[10, 50]上電阻率為2 Ωm。頻率取1/300 Hz, 計算地面上x=-25、 -15、 -7、 7、 15、 30 km處的視電阻率, 本文算法與積分方程法的結果對比如圖3所示, 兩種方法都能夠反映出垂直地層電阻率的變化趨勢, 結果幾乎一致, 說明了SEM算法用于2DMT正演的正確性。

圖3 IE與SEM的視電阻率

圖2b是在電阻率為100 Ωm的均勻半空間中嵌入一個電阻率為0.5 Ωm的異常體, 異常體在x方向上的位置是-0.5～0.5 km, 長為2 km, 寬為1 km, 上頂面離地面 0.25 km。 計算地面上x=0.5、 1、 2、 4、 8、 16 km處的視電阻率。頻率取0.1和10 Hz時的SEM與IE的計算結果對比如圖4所示, 兩種方法在不同頻域時的模擬結果幾乎一致, 誤差小于5%, 能夠反映出地下低阻異常體的特征, 說明了SEM算法用于2DMT正演計算的準確性。

2.2 二維模型譜元法效率分析

分別采用本文算法(SEM)和雙二次插值的有限元算法(FEM)計算模型COMMEMI 2D-0, 對二者的計算結果進行了對比。實驗中設計了由粗到細4套不同的網格, 在粗網格1上應用本文算法的4階譜元法, 在逐漸細化的網格上應用FEM進行計算。

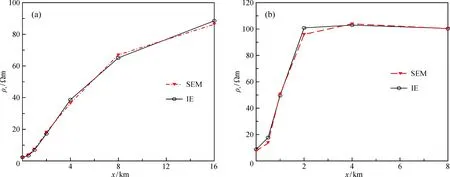
圖4 IE與SEM在頻率0.1(a)和10 Hz(b)的視電阻率

表1給出了SEM和FEM的自由度和計算時間比較, 圖5是FEM在不同尺寸的網格(Grid2、Grid4)和SEM、 IEM的計算結果比對。結果表明, 相同網格尺寸下SEM比FEM(Grid2)精度高、 耗時長, 但在同等精度下(FEM(Grid4))SEM所用計算時間更少。因此與FEM相比, SEM在粗網格下能夠保證精度, 減少計算時間。

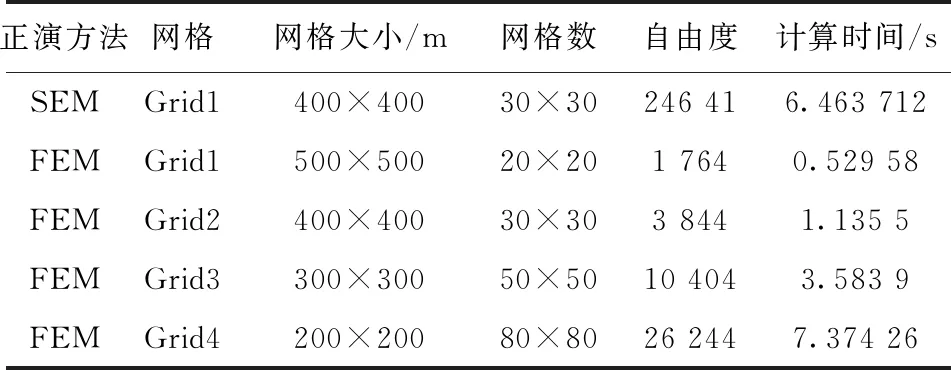
表1 譜元法與有限元法的計算時間對比

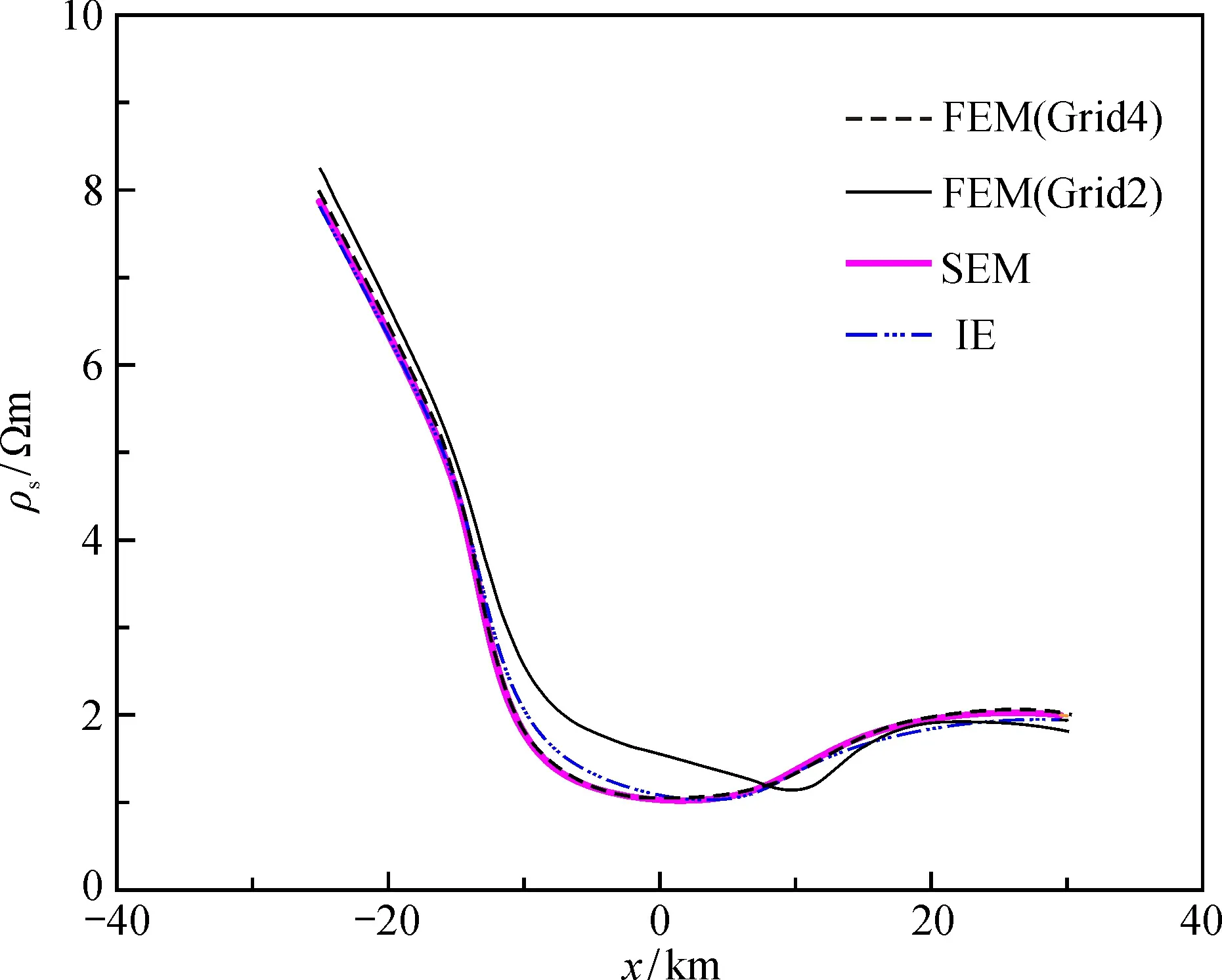
圖5 IE與SEM(Grid1)、 FEM(Grid2/Grid4)的視電阻率

2.3 水平地層中的異常體模擬

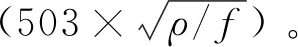
圖6 層狀地層低阻異常體(a)及高阻異常體(b)示意圖

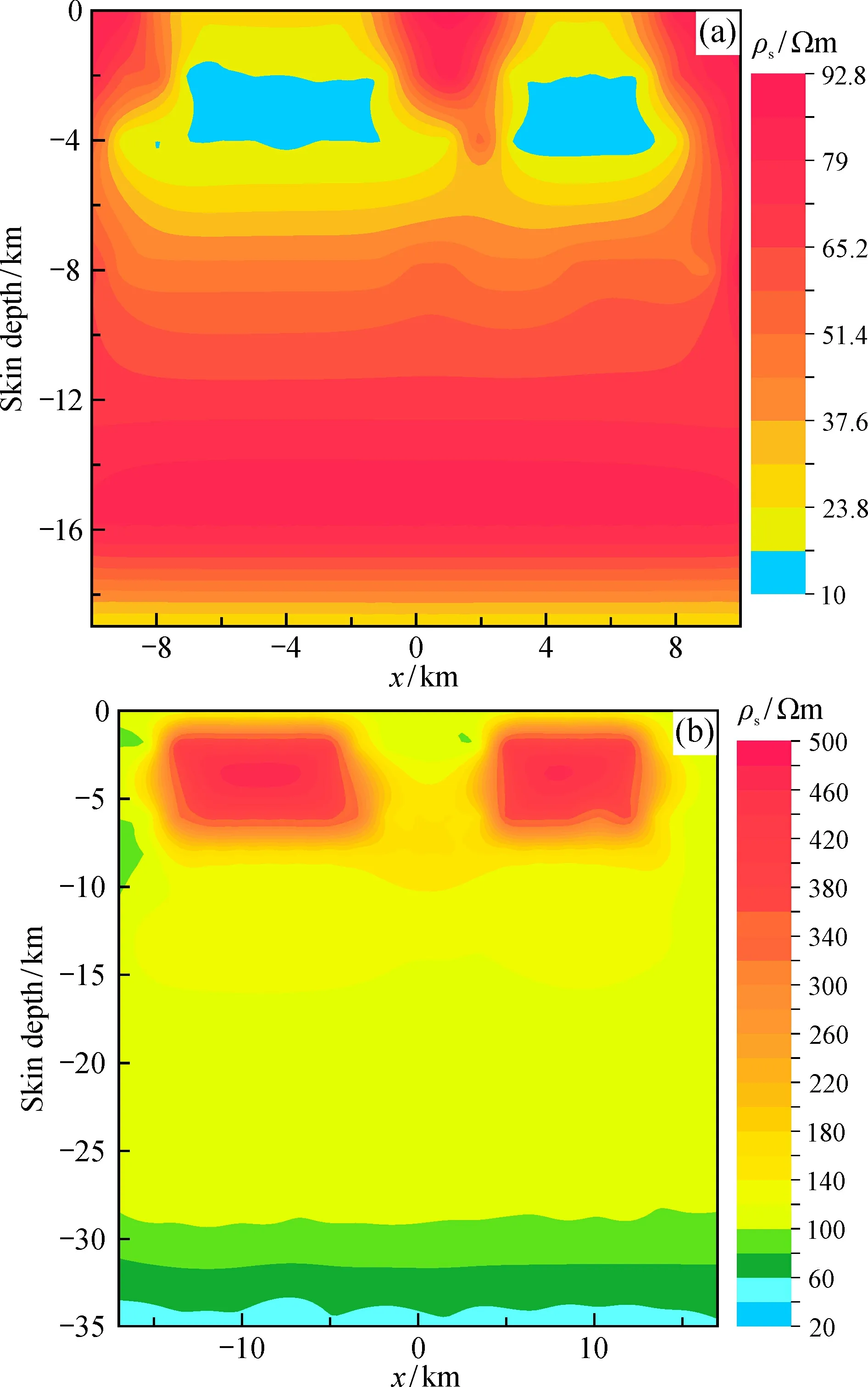
圖7 低阻異常體(a)及高阻異常體(b)視電阻率等值線圖

2.4 復雜地形模擬

2.4.1 地壘模擬 為研究起伏地形條件下平面波電磁響應, 算例3設計了一個地壘模型, 如圖8所示。在地壘模型中, 隆起部位上端寬為10 km, 下端寬為20 km, 凸起垂直高度為5 km, 地下均勻半空間的電阻率為100 Ωm, 空氣層電阻率取1010Ωm, 頻率為f=0.1、 1和100 Hz, 計算地面上的視電阻率和相位, 結果如圖9所示。起伏地形對視電阻率和相位均發生了畸變, 視電阻率隨著地形的凸起而增大, 且頻率越大響應越明顯, 與視電阻率相比, 相位受地形的影響更為明顯。

圖8 地壘模型示意圖

2.4.2 覆蓋層下的垂直斷層模擬 算例4設計了覆蓋層下有不同巖性的垂直斷層帶, 如圖10所示。上層覆蓋層電阻率為50 Ωm； 第二層是直立的斷層帶, 電阻率依次為30、 1、 100、 30 Ωm； 第三層為沉積層，其電阻率為100 Ωm； 第四層為基巖, 電阻率為0.1 Ωm。在頻率0.01～10 Hz范圍內進行正演計算, 得到如圖11所示的視電阻率分布。

可看出SEM能夠較好反映覆蓋層下的斷層, 在頻率為1 Hz的時候反映了覆蓋層的電阻率情況, 探測深度隨著頻率的減小而增大; 頻率在0.15 Hz時的視電阻率響應接近垂直斷層, 在x方向上-60～-20 km和30～60 km顯示了30 Ωm的異常, 在-20～10 km能夠準確得到低阻異常(1 Ωm), 在10～30 km清晰反映了高阻異常(100 Ωm); 再次減小頻率, 得到沉積層和基巖電阻率, 但在-15～10 km處受到低阻斷層異常的影響, 視電阻較低, 說明在層狀地層深部受到低阻斷層的影響較大, 而在覆蓋層中受到高阻斷層的影響更加明顯, 說明在層狀地層中淺部受到高阻異常的影響較大。

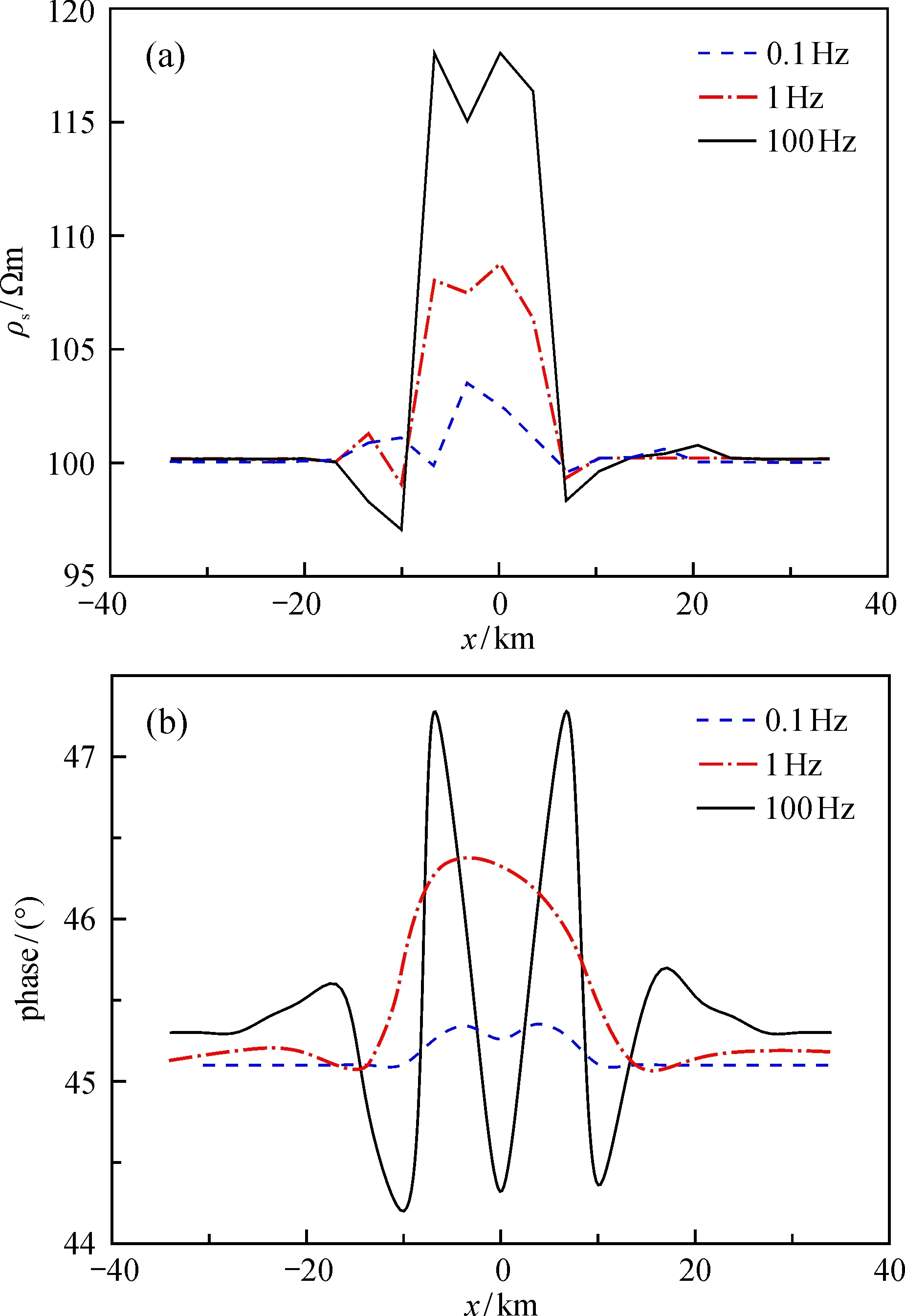
圖9 地壘視電阻率(a)及相位(b)

圖10 覆蓋層下的垂直斷層示意圖

2.4.3 簡單斷層與異常體模擬 算例5給出了一個更為復雜的地電模型(圖12), 其背景電阻率為100 Ωm, 存在電阻率為10 Ωm的4個低阻體, 分別位于x∈[0,14]、z∈[8,12];x∈[8,12]、z∈[26,30];x∈[20, 40]、z∈[8, 12], 在x為20～30 km是傾斜的;x∈[30,34]、z∈[22,30]。在其深度為2～3 km處有一條高阻斷層, 電阻率為1 000 Ωm，厚度為0.5 km, 在x方向20 km處向下錯動0.4 km。在頻率0.01～1 Hz范圍內計算得到頻率電阻率等值線圖(圖13)及不同頻率的相位曲線(圖14)。

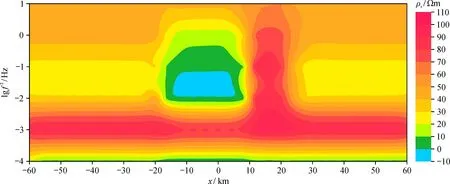
圖11 頻率視電阻分布

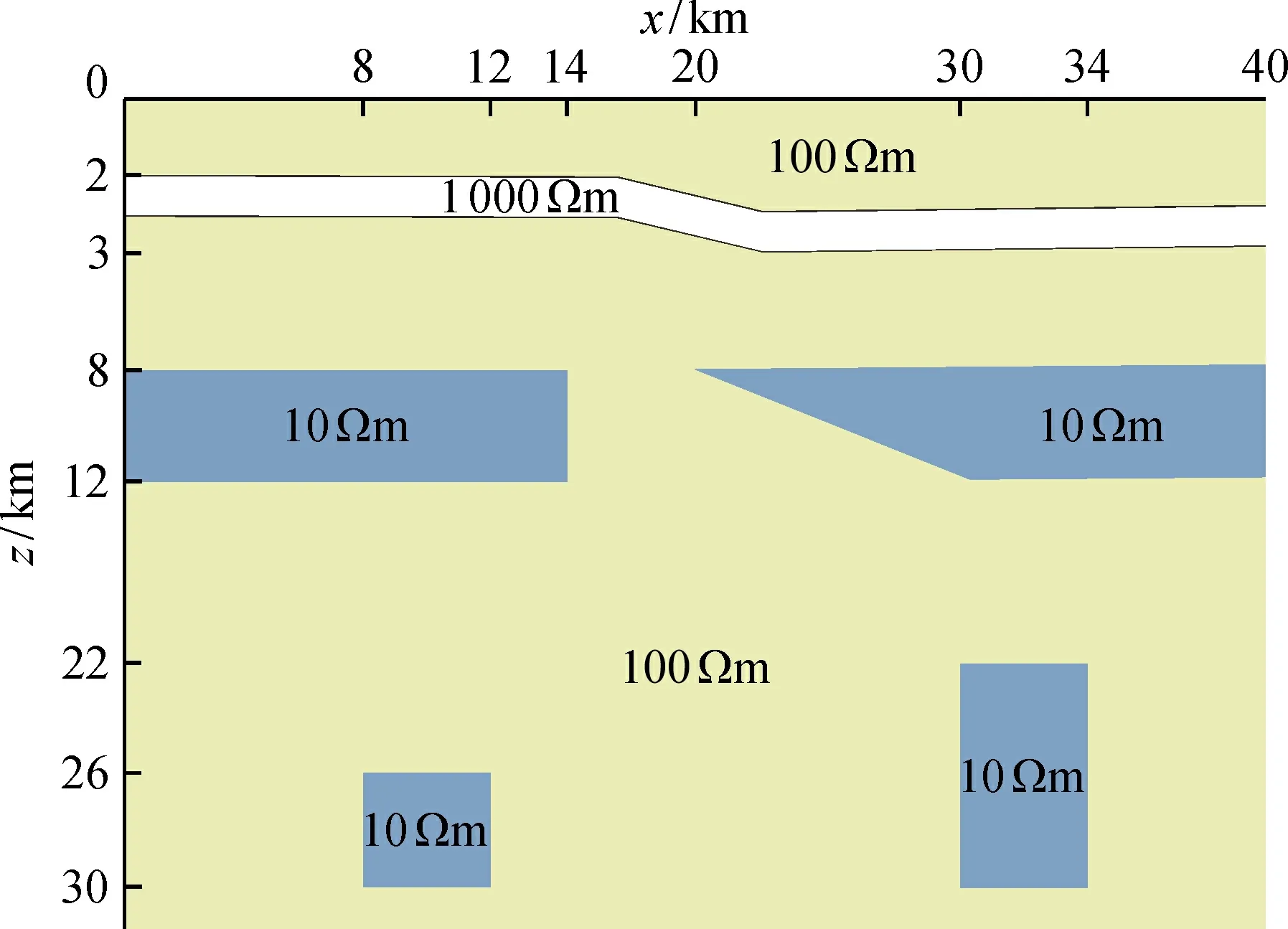
圖12 斷層巖體下的異常體示意圖

在圖13中電阻率等值線圖能夠精確反映地電結構, 清晰地顯示出高阻斷層和低阻體的存在, 右邊低阻傾斜體沒有完全吻合的原因是由于使用階梯網格和網格尺寸較大所致。

圖14顯示了不同頻率的相位變化曲線, 相位曲線更加清晰的反映了各個深度的地電結構。在地表1 Hz的相位清晰地反映了高阻斷層巖, 0.25 Hz的相位能夠明顯反映淺部兩邊低阻體和中間的背景場在0.063 Hz體現了上下低阻體中間位置的電場變化, 在低阻體所在位置均有變化趨勢, 在右端低阻體相位變化趨勢比左端低阻體相位變化平緩, 是由于受到右端傾斜低阻體的影響。 在0.037 Hz相位(圖14b)能夠清晰地反映底部低阻體和背景場, 能夠體現兩個低阻體在x方向的準確位置; 在0.024 Hz仍能夠反映低阻體的存在; 在0.01 Hz相位趨于平緩, 與背景場趨于一致。

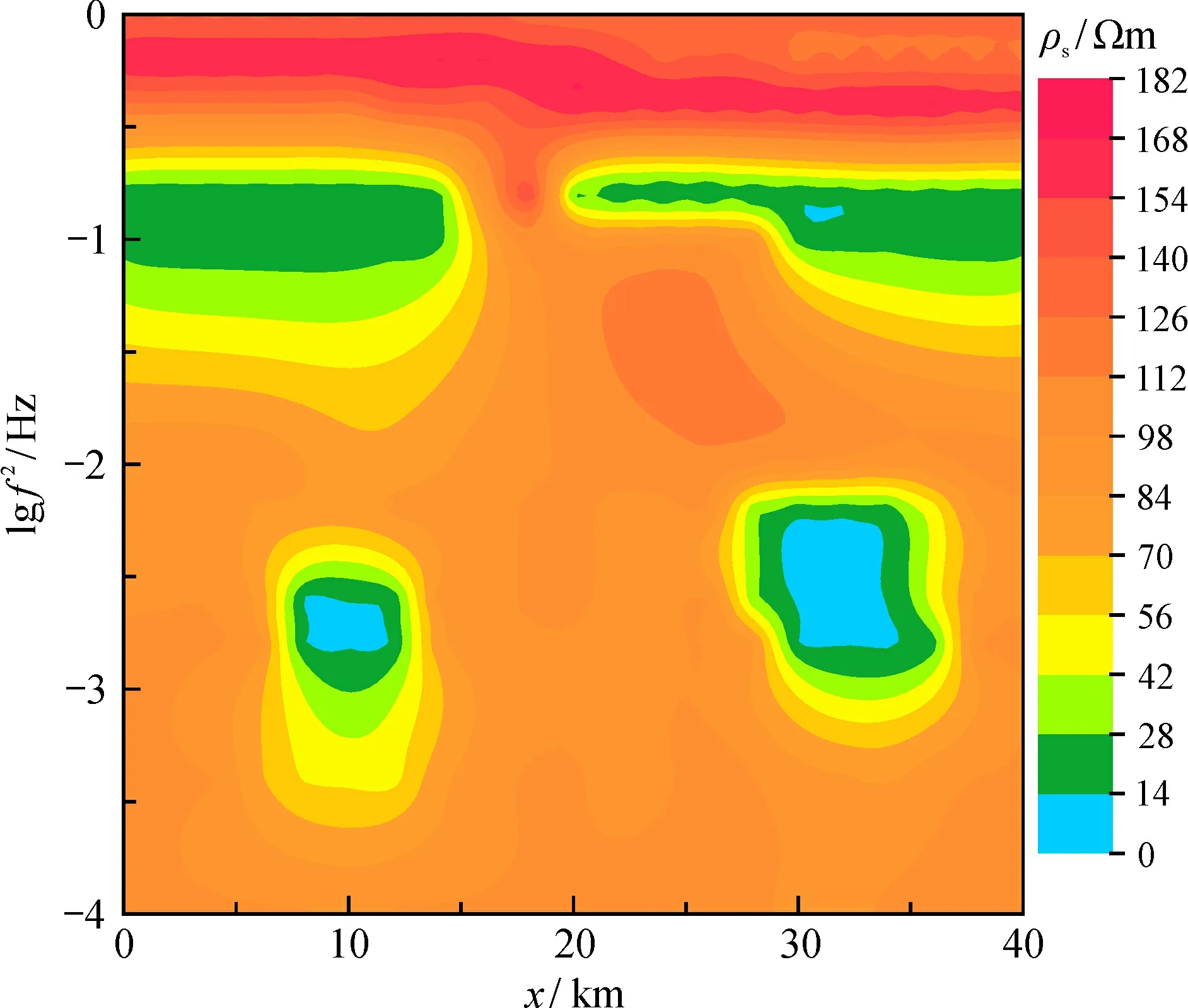
圖13 視電阻率等值線圖

2.4.4 深部地電結構簡化模擬 為研究深層流體穿過高阻巖石圈形成傳導通道時的電磁響應特征[31-33], 設計了算例6，如圖15所示。 第一層為水平層低阻體, 層厚1 km, 電阻率為30 Ωm； 第二層為高阻體, 電阻率為2 000 Ωm, 層厚20 km, 含有2個垂直狹窄的通道ρ1(其高度為7 km), 下半部分是一個地壘結構的低阻體, 電阻率為10 Ωm, 模型的類型取決于ρ1的選擇。觀測點取傳導通道中心點O和離中心點25 km的點R, 在頻率0.01～10 Hz范圍內進行計算，得到存在流體通道(ρ1區域)和不存在流體通道在不同觀測點處的視電阻率，如圖16所示。

圖14 不同頻率(1 、 0.25、 0.063、 0.037、 0.024、 0.01 Hz)相位曲線

圖15 深部地電結構簡化模型示意圖

圖中實線表示ρ1=2 000 Ωm, 即不存在垂直的流體通道情況下, 在中心點O和遠點R處的視電阻曲線, 低頻時無論觀測點R還是O都準確地反映了深部地電結構, 在高頻時, 遠點R的視電阻率高于中心點O, 這是因為中心點O處的視電阻率受到底部低阻地壘的影響; 虛線表示ρ1=10 Ωm, 即存在一個雙向低阻溶液流體通道, 在中心點O和遠點R處的視電阻率曲線, 視電阻率曲線和無導電通道的形態相似, 但在中心點O處, 視電阻率低于無流體通道時的視電阻率值, 在遠點R處視電阻率與無流體通道時的值一致。 由分析可知, 大地電磁響應對低阻流體通道有相當高的靈敏度, 這些通道將近地表和深部導體連接起來, 形成閉合的電流電路, 導致地殼和上地幔中的大地電流重新分布。

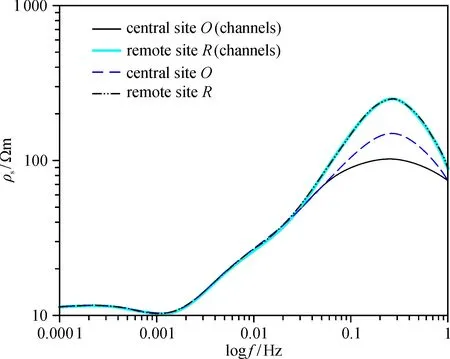
圖16 視電阻率對比

3 結 論

本文實現了基于譜元法的低頻平面波電磁場的數值模擬。在數值實驗中, 對國際標準模型COMMEMI2D-0、 COMMEMI2D-1進行計算, 驗證了算法的有效性和準確性, 與有限元方法對比, 表明了本文算法具有更高的計算精度和效率, 通過設計復雜地電模型, 表明了譜元法應用于大地電磁正演的有效性, 并進一步分析了這些典型模型的大地電磁響應特征, 對實際工作提供了借鑒和指導意義。為進一步提高算法的實用性和計算效率, 將在以后的研究中考慮將有限元和譜元法相結合。