基于SG算法和BP神經網絡的角度傳感器信號處理研究

(內蒙古民族幼兒師范高等專科學校，內蒙古自治區 鄂爾多斯 017000)

0 引言

電解角度傳感器具有良好的耐用性，因此在包括工業機械臂在內的多個領域得到廣泛的應用[1]。眾所周知，傳感器精度是決定系統控制精度的主要因素，因此提高角度傳感器的輸出精度具有重要的現實意義。由于設計因素和材料因素的原因，電解角度傳感器在不同環境溫度下會出現誤差，尤其在高層戶外的環境，這種誤差效果更為凸顯。為此，提出一種提高角度傳感器輸出精度的解決方法。該方法首先使用SG算法[2]對原始傳感信號進行預過濾處理，隨后使用BP神經網絡[3]對包含對角度傳感器信號和環境溫度傳感信號多階數輸出信號進行誤差估計，最終達到抵消溫度誤差、提高傳感角度的目標。

1 電解角度傳感器的工作原理

角度傳感器廣泛應用于天線定位、航空電子、坡度或傾斜監測和車輛姿態監測等領域。為保證角度傳感器的工作可靠性，本文選用電解角度傳感器。電解角度傳感器結構獨特，適用于窄角和寬角范圍的測量，同時又保持了緊湊的尺寸和較高的精度，且具有成本低、批量生產可能、功耗低、重復性好和可靠性好等優點。電解角度傳感器的工作原理如圖1所示。傳感器的主體是用各向異性KOH蝕刻法制備的填充導電電解質的大體積硅腔，并采用頂部玻璃薄片密封[4]。當角度傳感器水平時，正極和負極均浸入電解液中，相對于普通電極，正極和負極之間產生平衡的電阻信號輸出。當傳感器傾斜時，電極的浸入表面積會發生變化，一個電極的浸入面積增加，另一個電極的浸入面積減小。電阻的不平衡比與傾角成正比，因此通過測量電阻即可得出傾角。

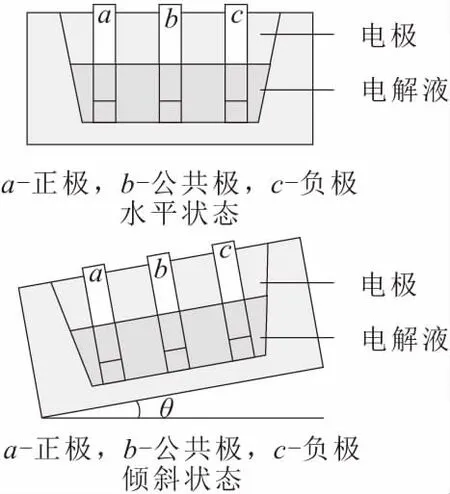
圖1 電解角度傳感器的工作原理

2 SG算法

作為局部多項式回歸方法 SG濾波算法是通過最小二乘解[5]可以得到給定數據窗大小(2L+1)的優化曲線擬合多項式，因此，SG濾波器可以作為一個信號平滑算法[6]。假設a(k)是一組采樣數據樣本序列。每一個數據點(如k=0)周圍有一組(2L+1)個樣本，形成一個擬合多項式，表示為[7]

fi=a0+a1i+a2i2+…+apip=

(1)

SG算法通過將待處理數據中某一連續的數據點選用相應的擬合階次進行最小二乘法多項式擬合，進而將擬合得到的曲線在數據中心點處的取值作為濾波后的數據值，并依此對其他待處理數據重復此過程。從而達到對所有數據進行濾波的目的。SG算法的具體濾波過程如下。

設x(n)中的一組數據為x(i)，i=-M，…，0，…，M。通過構造一個p階多項式fi來擬合x(i)。

(2)

ak(k=0,…,N)為擬合系數；N為多項式階數。得到fi的目的是使如式(2)所示的誤差項最小化。

(3)

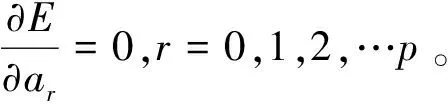
(4)

通過確定多項式階數N即可求出Fr和Sk+r。將其代入式(4)中則可計算求出擬合系數a0，a1和ap，從而確定擬合多項式fi。最后通過擬合多項式fi對輸入的采樣信號進行平滑計算從而求出濾波后的輸出采樣數據序列。

本文使用SG算法對傳感器的采樣數字信號進行濾波計算。當SG算法參數M=15且P=3 時，濾波前后的采樣數據序列如圖2所示。由圖2可以看出，SG算法有效地減少傳感器輸出信號的擬合誤差，為建立神經網絡模型提供足夠準確的傳感數據。

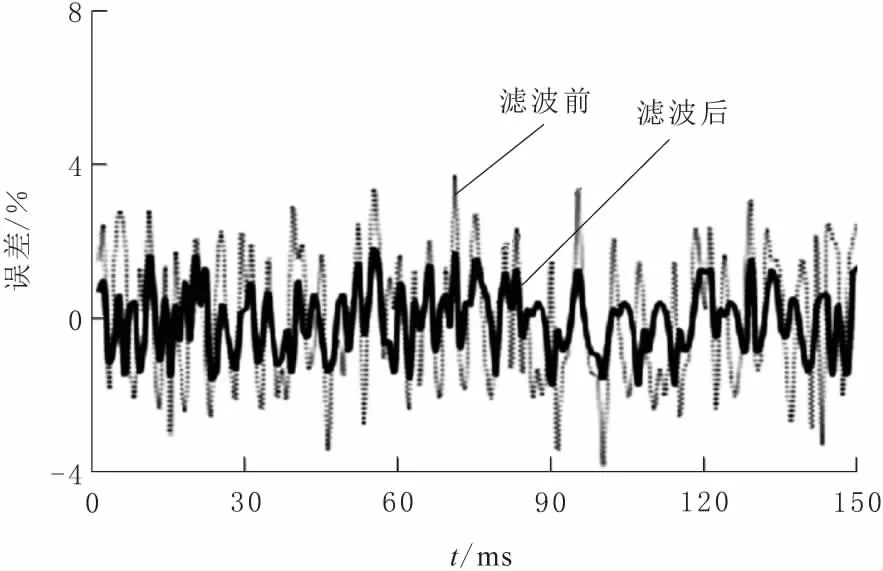
圖2 傾角傳感器濾波預處理后誤差對比

3 BP神經網絡模型

由于傳感器的導電電解質和正負電極在環境溫度變化下會導致電阻率出現不同程度的變化，從而影響角度傳感器的輸出信號的精度[8]，因此使用BP神經網絡對輸出信號所包含的角度信息進行糾正，以抵消環境溫度對輸出角度信號的干擾。所建立的3層BP神經網絡結構如圖3所示。為了實現從傳感器輸入信號和環境溫度值到輸出角度信號的復雜非線性映射，分別選擇非線性tansig函數和線性purelin函數作為隱藏層和輸出層的傳遞函數[9]。

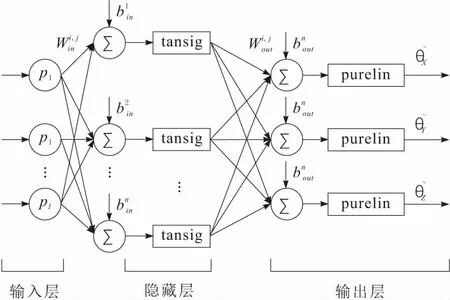
圖3 三層BP神經網絡結構

設角度傳感器的采樣值序列為θ，其采樣時間為10 s；t為采樣通道總數，該信號已經被SG過濾算法處理；aj為第j個溫度傳感器的采樣值序列，采樣時間為10 s；k為采樣通道總數。即

(5)

通過m階非線性模型估計輸出角度

(6)

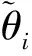
(7)

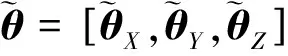
(8)

從式(7)和圖3可以看出，輸入神經元的數量溫度采集通道的數量和角度傳感器的數量有關。輸出層有3個神經元，代表3個方向的角度。中間層神經元數目n不確定。輸入層和中間層神經元的數目對關節角估計的精度都有很大的影響，因此將根據網絡性能選擇合適的神經元數量。

一旦建立了網絡的精確結構，那么最重要的事情之一就是訓練網絡的權值和閾值。經過數據采集和預處理，利用處理后的角度傳感信號和溫度傳感信號構造輸入矩陣，利用處理后的3個維度的角度向量構造目標矩陣。所有的數據點也被劃分為2個部分：訓練和驗證。在所有的實驗中，每個實驗提取20 s的信號，10 s用于訓練，另外10 s用于驗證。最陡下降反向傳播是一種最基本的反向傳播算法，其最大的缺點是在整個網絡訓練過程中學習速率保持不變，因此算法的實際性能對學習速率的正確選擇非常敏感。一旦沒有正確選擇學習速率，可能會出現2個問題：當學習速率過大時，訓練過程可能會發生振蕩，變得不穩定；另一個問題是訓練過程非常緩慢，網絡收斂需要很長時間。事實上，由于最優學習速率隨迭代次數的變化而變化，對于一定的網絡，并沒有固定的最優學習速率。針對最陡下降反向傳播算法的不足，提出了一些改進算法。動量變學習速率BP算法(GDX)是改進的BP算法之一，也是本研究中使用的算法。

BP神經網絡訓練參數設定如表1所示。為了提高訓練效率，本文對輸入數據進行歸一化處理，使得所有的輸入數據取值區間限定在[0～1]之間。歸一化計算

(9)

yi為歸一化后數值；xi為原始數值；xmin為最小輸入數值；xmax為最大輸入數值。

表1 神經網絡參數表

4 算法驗證及分析

4.1 神經元數量的確定

如上所述，如果模型階數和隱層神經元數目選擇不當，角度估計誤差會很大，因此需要在算法驗證前首先在MATLAB環境下進行仿真實驗以確定模型階數和神經元數量。實驗所用的網絡模型為

net=newff(min max(traininput),[20,3],

{‘tansig’,‘purelin’},‘trainlm’)

(10)

net為目標BP神經網絡模型；newff為在MATLAB 7.0中生成的BP神經網絡函數；minmax()用以求解輸入樣本參數的最小值和最大值；[20，3]中“20”代表中間隱含層的神經元個數，“3”代表輸出層神經元個數；{‘tansig’，‘purelin’}分別表示輸入層到隱含層和隱含層到輸出層的傳遞函數；‘trainlm’為本研究所設計的訓練函數。

在模型階數和隱層神經元數發生變化的設置下，進行4次反復試驗，得出的角度平均估計均方根誤差變化如圖4所示。對圖4進行分析可知模型階數(即輸入通道)并不是越多越好，冗余的采集數據會引起網絡振蕩。從圖4a可以看出，選擇模型階數為20時，隱藏層神經元的最優數量為20，輸入向量長度為60。由圖4b可知，當隱藏層神經元數量為20時，最優模型階數為20。由此可知最優的模型階數和隱藏層均為20。

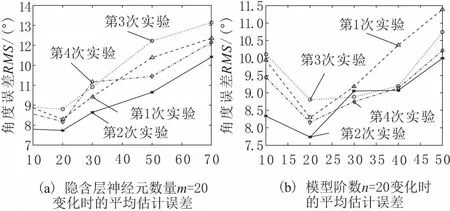
圖4 當隱層神經元數目和模型階數m變化時，角度估計均方根誤差

4.2 算法驗證

在溫度精確的實驗環境下將18個角度傳感器固定在三軸轉臺上進行算法驗證實驗，同時在實驗環境中設置2個溫度傳感器。轉臺的角度值作為算法輸出的角度值的標準參照數值。實驗共采集160組傳感數據，每組數據包括10個角度傳感數據和10個溫度數據。然后使用SG算法對采集的傳感數據序列進行平滑濾波處理。最后將處理后的傳感數據分為2組：124組訓練數據和36組測試數據。

訓練過程中的BP神經網絡的誤差收斂曲線如圖5所示。由圖5可知，在完成165次迭代時，BP神經網絡的輸出誤差降至0.000 099，顯示出了令人滿意的收斂速度。

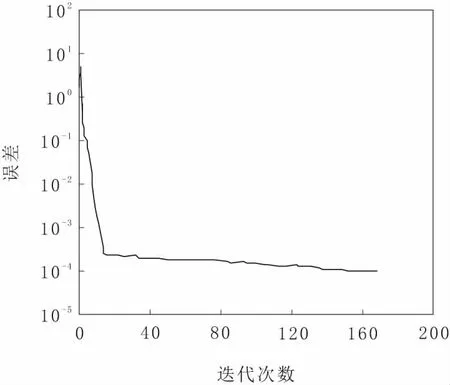
圖5 神經網絡誤差收斂曲線

使用測試數據對經過訓練的BP神經網絡進行測試的結果如表2所示。表2中真實值和擬合值均為3個方向角度的平均值。表中“組合模型”是采用完成訓練的BP神經網絡對經過SG算法處理的36組傳感數據進行擬合的相對誤差；“原始數據”為采集的原始角度傳感數據的平均值；“SG算法”是對原始傳感數據進行濾波后的平均值。對這3列數據進行分析能夠得出以下結果：經過結合SG算法和BP神經網絡組合模型處理后的傳感數據具有最小的擬合誤差。

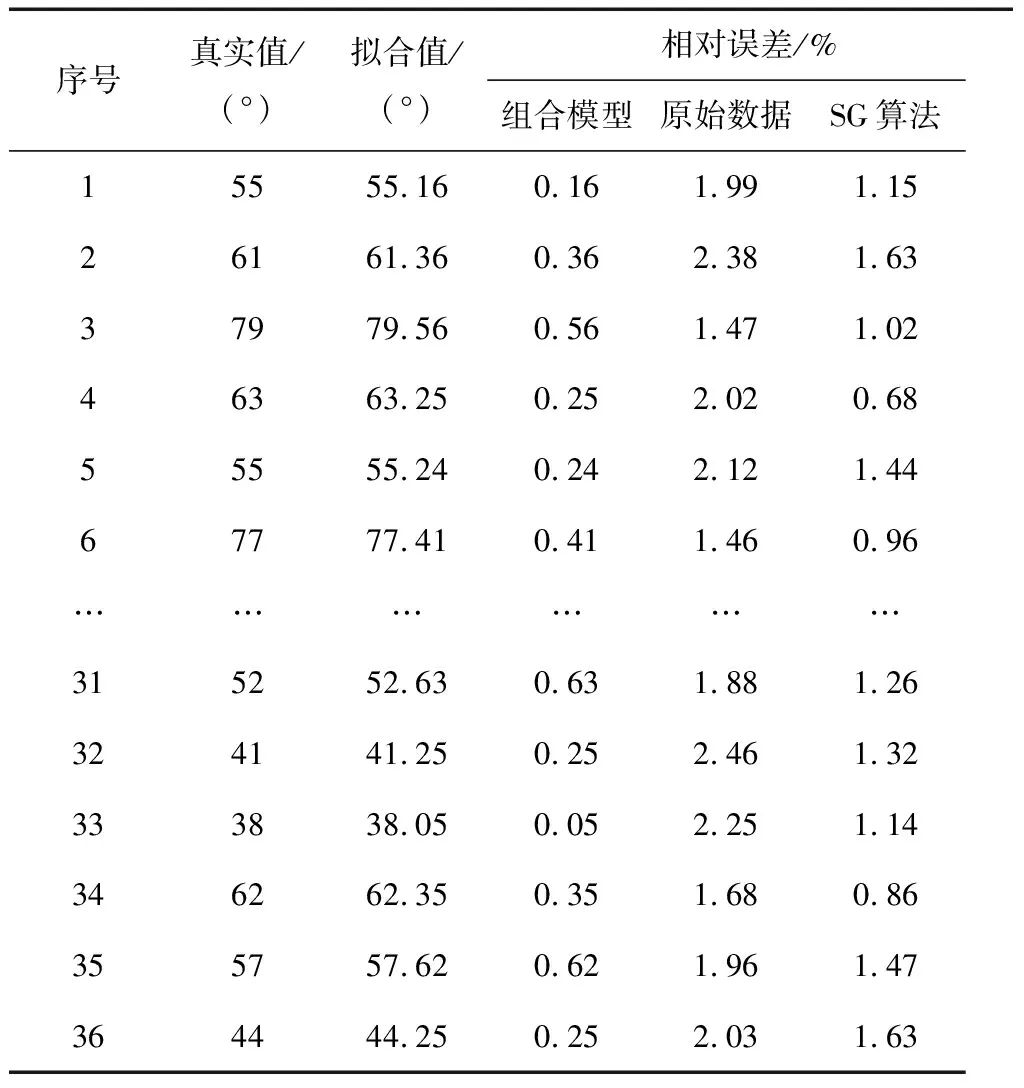
表2 檢驗樣本數據誤差比較

5 結束語

本文針對角度傳感器在實際使用中容易收到環境溫度干擾出現誤差的問題，提出采用SG算法和BP神經網絡組合算法進行信號處理以降低誤差干擾的解決思路。該方法是首先使用SG算法對傳感信號進行平滑規律，然后使用BP神經網絡對傳感信號進行擬合估計。實驗結果表明，在選擇合適的傳感數據采集通道數量和建立最優的BP神經網絡規模的前提下，該方法輸出的傳感數據能夠有效抵消環境溫度的干擾。