基于最速下降的矢量光刻模型掩膜優化

(廣東工業大學 廣東 廣州 510080)

引言

傳統的光學鄰近校正技術已經難以滿足生產的需要[3]，而作為最優化算法的反向光刻技術，在理論上可以找到最佳的掩膜去補償圖案的畸變[4]，因此，運用分辨率增強技術進一步提高光刻系統的圖像精確度一直是該領域研究有效手段。最速梯度下降是是非線性最優化常見的方法，它的主要思想是使用目標函數和約束條件定義或推導出代價函數，通過計算代價函數的梯度和選擇合適的更新步長來確定最優化下降方向和大小。

一、光刻系統的矢量模型

光刻投影成像系統主要分為兩個部分：投影光學效果(耦合成像)和抗蝕效果。對于照明光源波長為193nm且NA大于0.4的光刻系統，硅晶圓表面的成像過程必須考慮光波通過光學投影儀器元件時的偏振狀態，如圖1所示

圖1 矢量光刻模型系統

(1)

其中，J(αs,βs)是位于點(αs,βs)處光源的強度，且Jss=∑(αs ,βs )J(αs,βs)是所有對成像做出貢獻的點光源強度之和。且下式在投影光刻中通常被認為是頻域等效低通濾波器[5]：

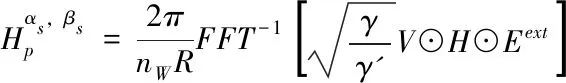
(2)

光刻膠抗蝕作用同樣使用sigmoid激活函數來描述[6]：

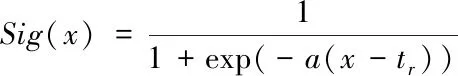
(3)

其中，a描述了激活函數的陡峭程度，tr表示激活的閾值。

二、反向光刻技術

一般來說，反向光刻技術ILT中的掩模合成包括兩步，第一步是對光刻系統成像形成過程的數學建模，第二步是迭代掩膜變量，尋找適當設計的成本函數的最小值，以提高輸出圖像的保真度。因此，ILT的性能主要取決于成像地層模型的精度和優化框架中反演成像計算的效率。光刻系統與NA小于0.4的標量成像模型提供足夠的準確性。從交叉領域來說反向光刻算法是基于非線性最優化算法的一種凸優化理論模型，自誕生以來就以其強大的尋優能力著稱，然而由于計算機性能的限制，以前并沒有被廣泛運用。而后，隨著計算機計算能力的大幅提高，反向光刻算法ILT備受關注。

三、最速梯度下降

最速梯度下降法的流程為：

第一步、定義代價函數F(x);

第二步、計算代價函數在當前點的梯度dxk，其中x的上標k代表變量在第k次對應的信息;

第三步、算法更新規則：xk+1=xk-S?dxk,其中S是更新步長，取值范圍通常在0.1至0.3;

第四步、計算xk+1處的代價函數，判斷是否符合條件，若不符合則不斷重復步驟第二步和第三步直到滿足條件為止；

其演變過程如圖4.1所示，若首次在x1點處計算出的梯度是dx1，選擇合適的步長更新后變量假設位于點x2處，且x2處的代價函數F(x2)及梯度的絕對值|dx2|均小于在x1處的代價函數F(x1)和梯度的絕對值|dx1|。同樣的，變量可計算梯度并逐漸更新至x3、x4、x5,當dxk處的值足夠小時(即梯度減小到接近零時)，在理論上算法迭帶結束。但是，這樣只能確定在有限的區間內代價函數達到最小值，即局部最小值。另一方面，若初次更新的位置處于x5且更新步長S過大，變量更新則會由x5至x4,又因為|dx4|>|dx5|，變量會逐漸由x4更新至x3、x2、x1，即優化并沒有收斂反而發散。

四、實驗結果

圖2 基于SGD逆優化結果

如圖3所示，我們給出了基于分層模型的SGD逆優化結果。其中，從左到右分別是照明光源、掩膜和投影物像，從上到下的兩組組實驗是未優化實驗結果、使用SGD優化的結果。值得注意的是，這兩組實驗均使用相同的照明系統，用于逆優化的初始化掩膜相同，且在本實驗中我們僅優化了主特征區域。觀察后兩組實驗我們可以發現使用SGD算法的優化結果還是比較明顯的。

五、結論

實驗結果表明，SGD算法有明顯的的優化效果。不過實驗中根據該算法的代價函數總體趨勢是一個下降的過程，局部下降曲線不平滑的現象，SGD也存在步長時小優化速度慢，步長大容易發散的缺點，因此想對優化過程進一步完善，接下來要從自適應調節步長以及擴大每次迭代步長入手。