考慮降雨入滲效應的高邊坡開挖數值模擬研究

駱文進，鄭曉蕾，王麗英

(重慶建筑工程職業學院土木工程系，重慶400072)

0 引 言

隨著我國水利工程的高速發展，對水利工程的邊坡設計和施工要求也不斷提高[1]。工程上規定坡高大于20 m、小于100 m的邊坡為高邊坡，其穩定性問題一直是國內外學者重點關注的問題之一[2]。隨著高邊坡的建設量越來越大，水利工程滑坡事故的數量近年來有所增加，給工程的安全與經濟造成巨大危害[3-5]。由于水利工程邊坡的地質條件復雜，坡體形式各異，氣候差別明顯等因素，導致不同地區的邊坡產生滑動、崩塌和失穩等工程事故的原因各不相同[4]。因此，針對高邊坡的穩定性問題開展研究具有重要的現實意義。

有限元數值模擬分析是研究建筑、道路、地基和邊坡等工程建設安全性的一種較為成熟的方法。早在20世紀60年代，就有學者將有限元方法應用于邊坡穩定性分析[6]。發展至今，有限元數值模擬法已經成為目前工程界進行邊坡穩定性分析的最常用方法之一。有限元數值分析法可以考慮不同邊坡巖土體的應力-應變本構關系，理論體系相對嚴密，也可以通過改變模型的形式和材料參數以模擬不同邊坡形狀和支護體系的工況，對于邊坡變形和滲流的耦合計算有很大優勢[7]。

巖土體的水文條件是影響水利工程高邊坡長期穩定性的重要因素之一。邊坡經過開挖后會形成臨空面，使巖土體受降雨入滲影響而引起邊坡穩定性下降。當前，國內外學者利用多種數值模擬軟件對邊坡在降雨入滲工況下進行了穩定性分析。楊龍等[8]采用Geo-slope軟件分析了降雨條件下高邊坡的實際滲流場，得到了邊坡穩定性與降雨量之間的關系，指出降雨影響深度是影響邊坡穩定的重要因素；鐘佩文等[9]利用FLAC 2D數值模擬軟件建立了土質邊坡的數值模型，指出降雨入滲作用使土體的強度顯著減小，導致塑性區逐漸擴展形成剪切帶進而誘發滑坡事故；葉帥華等[10]通過PLAXIS 2D有限元軟件對降雨入滲條件對多級黃土高邊坡的變形的影響進行了數值模擬，得到了邊坡穩定性指標在降雨入滲中的變化規律；劉子振等[11]建立了粘土質臨危邊坡體三維數值模型，依據極限平衡理論與強度折減法對邊坡體在降雨入滲影響下的穩定性進行了評價，并獲得了坡體潛在滑動面的位置和形狀。

在長期的環境變化影響下，土體力學性質易發生劣化，進而影響高邊坡的服役性能。在工程中，忽略降雨入滲的影響往往會引發邊坡發生突然性滑塌。因此，本研究針對某水利工程沿線的黃土邊坡常年受降雨入滲作用的影響特征，研究降雨入滲深度與設計坡比對高邊坡穩定性的影響，采用FLAC 2D數值分析軟件對黃土高邊坡進行建模，旨在通過數值分析的結果為水利工程高邊坡的建設提供參考。

1 邊坡穩定性分析方法

目前，工程界常用的邊坡穩定性分析方法有極限平衡法和有限元強度折減法[11]。其中，極限平衡法已經在邊坡工程中應用了幾十年，其適用性已經得到了廣泛驗證，但也具有一定的局限性。如運用該法不能對巖土體應力-應變關系的差異性進行綜合考量，并且該法僅通過幾個基本假定直接求解滑動面穩定性安全系數，求解過程缺乏對實際工況的反映，獲取的結果精確性較差[12]。

隨著有限元理論和應用軟件的快速發展，越來越多的學者采用數值模擬分析法評價水利工程高邊坡的穩定性。FLAC 2D分析軟件作為一種通用的數值模擬軟件，能對各類復雜工程問題進行模擬，在邊坡工程分析中得到了大量的應用[13]。FLAC 2D分析軟件對不同類型的邊坡工程有較強的適用性，并可以采用各種編程語言對計算程序進行二次開發，以此克服采用極限平衡法時需預先假設滑移面形狀與位置的缺陷。基于FLAC 2D軟件的有限元數值模擬能準確地得到邊坡開挖過程中的位移場和應力場分布形式，且可以定量地反映邊坡體穩定性的變化規律[14]。

本文以某水利工程黃土質高邊坡為工程背景，分析降雨入滲深度和設計坡比對邊坡穩定性與滑動面的影響。根據有限元單元強度折減法進行邊坡穩定性分析的過程見圖1。圖1中，k1、k2為有限差分法分析中的2個極限值(k2≥k1)；η為給定的誤差。在分析過程中，以計算結果的收斂為有限差分法分析結束的判據，在軟件中輸入抗剪強度參數，即粘聚力c和內摩擦角φ，采用二分法對強度參數進行折減以逼近失穩極限；當計算得到的折減系數ra<10-5時表示計算達到收斂狀態；若結果不收斂，則重復上述計算直到折減系數滿足收斂要求。本計算采用Fish語言編輯命令流，再導入數值模型進行計算，命令流的下限k1和上限k2取值為0和2。

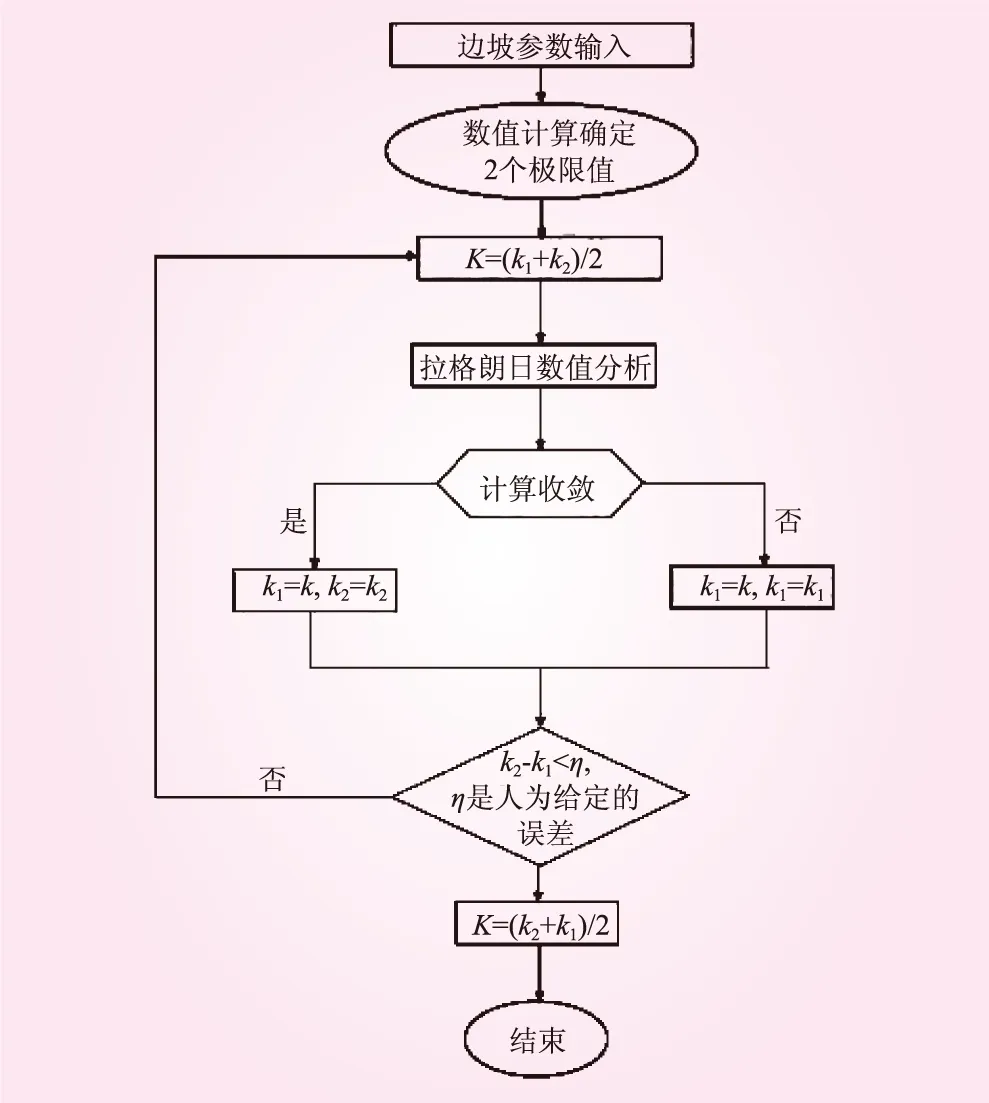
圖1 計算流程示意

2 模型建立

2.1 數值模型參數

現場地勘結果表明，邊坡自上而下分布粉質黃土、砂土、砂質粘土層和深厚的風化泥巖層。該邊坡的坡體延展方向近似為東西向，長約280 m，寬約為64 m，坡體高約22 m。在土工試驗室內開展試驗，獲得了該邊坡不同類型巖土體在天然與浸水狀態下的物理力學基本參數，具體數值見表1。

表1 模型材料參數

2.2 邊坡的有限元模型

參照該水利工程高邊坡的設計圖，建立了二維邊坡的數值模型。為了簡化有限元數值模擬計算的過程，在計算模型中對邊坡頂端設置自由約束，側面和底面邊界設置位移約束。按照兩級放坡模式建模，模型坡高設置為22.0 m，坡前的場地長度設為15.0 m，坡后的場地長度設為22.5 m，平臺長度設為5.0 m。利用FLAC 2D軟件中的平面應變單元進行邊坡模型的網格劃分，邊坡模型共包含725個節點，5 540個計算單元，建立的模型網格見圖2。在數值模擬中，通過改變降雨入滲深度h(1.0～6.0 m)以反映降雨量差異對邊坡穩定性的影響；通過改變坡比以反映開挖坡度對邊坡穩定性的影響。采用摩爾-庫倫的本構關系進行數值計算，基于結果分析不同設計坡比與降雨入滲深度對邊坡穩定性的影響規律。

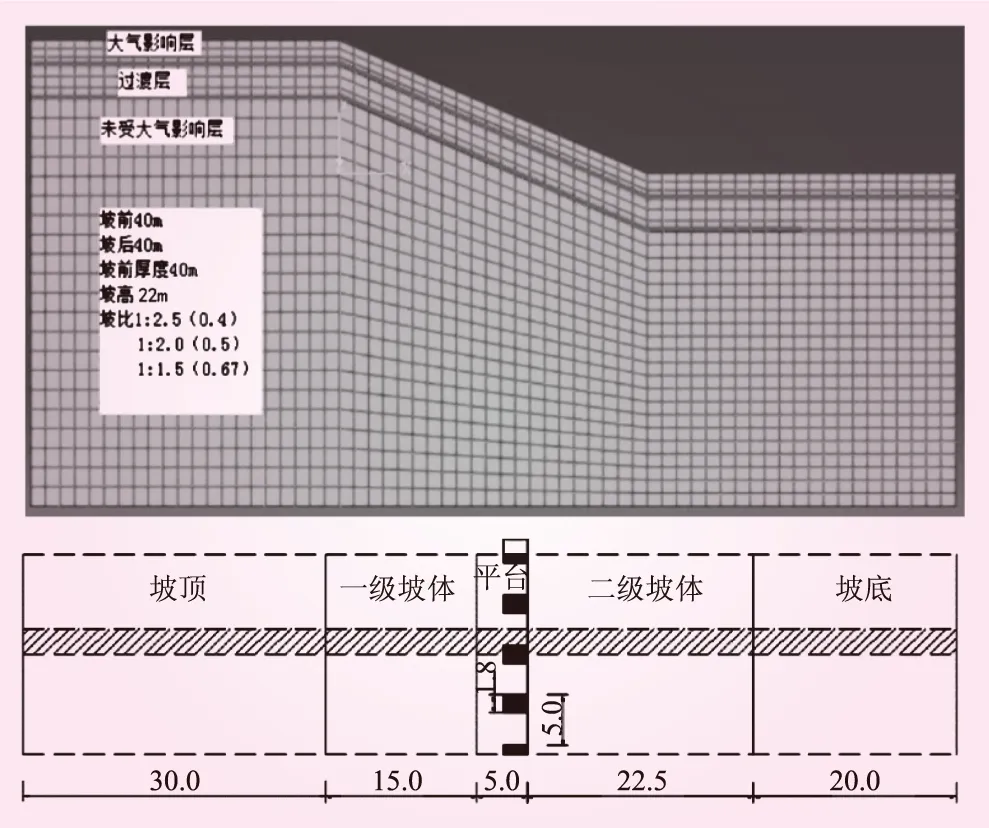
圖2 數值模型(單位：m)

3 數值計算結果

3.1 穩定性安全系數Fs

邊坡的設計坡比等于邊坡的高度與長度之比，坡比值越大代表該邊坡越陡峭。本研究通過計算，得到了坡比為1∶1.0、1∶1.5和1∶2.5這3種工況下的邊坡穩定安全系數及相應的位移場。同時，為了反映降雨量大小對邊坡穩定性影響，采用不同降雨入滲的影響深度(0～6 m)代入數值模擬模型，得到邊坡穩定性安全系數結果見表2。

表2 高邊坡的穩定性安全系數計算值

為了更清楚地反映邊坡的設計坡比對于穩定性安全系數Fs的影響，繪制不同坡比模型安全系數隨降雨入滲深度變化關系圖，見圖3。從圖3可知，降雨入滲深度從0到6 m不斷增加的過程中，坡比為1∶1.0、1∶1.5和1∶2.5的邊坡穩定性安全系數Fs分別下降了15.6%、9.9%和6.7%。可見，設計坡比的增加對邊坡的穩定性有明顯不利影響。而對于入滲影響深度為0的邊坡，在坡比由1∶1.0減小到1∶2.5過程中，Fs從1.651提高至2.280，即邊坡穩定性安全系數提高了38.08%。隨著降雨入滲深度的增加，Fs逐漸減小。此現象說明降雨量越大，降雨入滲的影響深度越大，則邊坡的穩定性就越差。

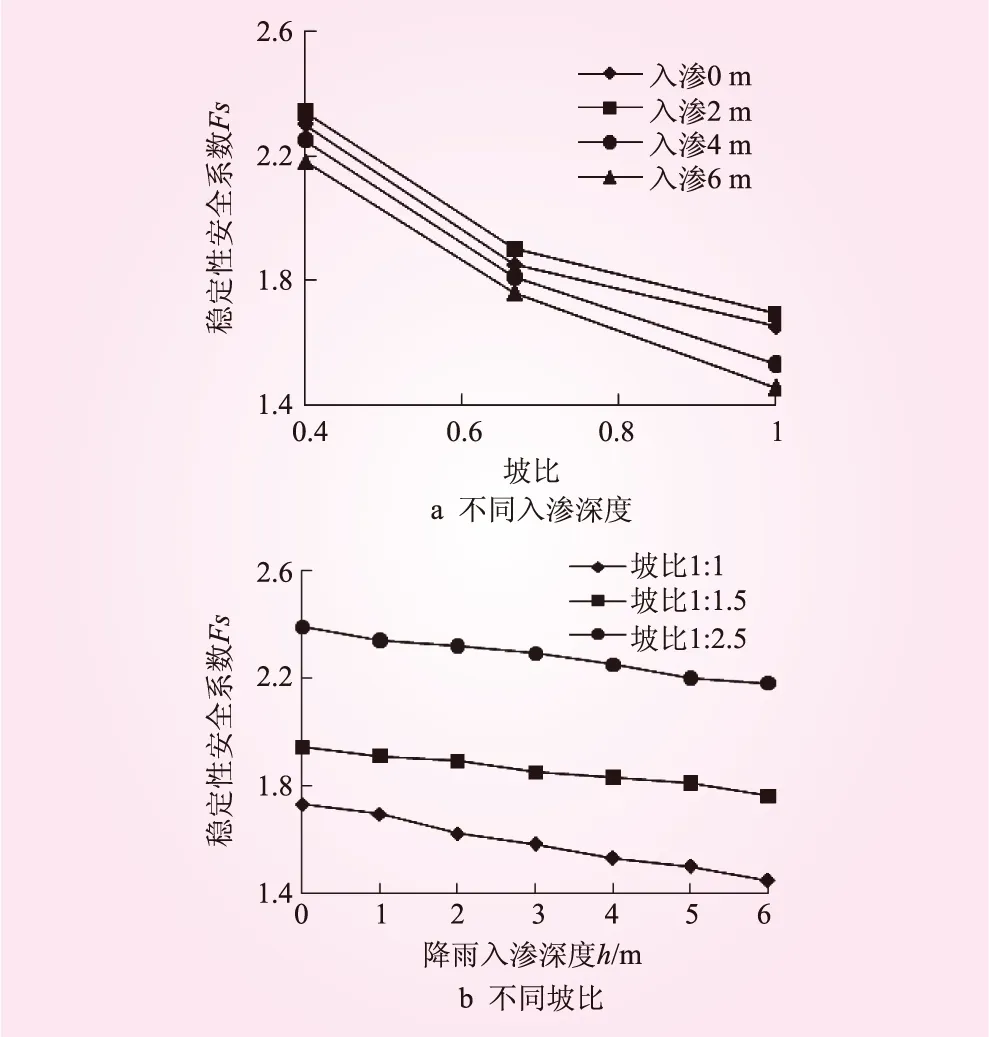
圖3 邊坡穩定性系數變化

3.2 降雨入滲深度和設計坡比對塑性區分布的影響

不同降雨入滲深度邊坡穩定臨界塑性區見圖4。從圖4可知，不同降雨入滲影響深度下邊坡的臨界狀態塑性區分布有如下規律：

圖4 不同降雨入滲深度邊坡穩定臨界塑性區

(1)入滲深度為0時，邊坡的塑性區從坡腳剛剛開始形成，潛在滑動面呈類圓弧形狀。隨著入滲深度從0增加至4 m的過程中，坡腳的塑性區逐漸向上發展并貫通，當入滲深度為4 m時，坡體在入滲鋒面處形成狹長的塑性變形區。

(2)入滲深度為5 m時，入滲鋒面的塑性區基本連通并通過坡腳形成潛在滑動面；當入滲深度達到6 m時，坡體的潛在滑動面大致形成，此時邊坡的穩定安全系數Fs最低。在降雨入滲深度從0發展到6 m時，潛在的滑動面位置從邊坡的深部逐漸向淺層坡面發展。

因此，降雨入滲深度對于水利工程高邊坡的塑性區分布有著直接影響，降雨入滲深度越大，越容易形成潛在的滑動面，從而誘發坡體的局部和整體滑塌。

以降雨入滲深度為6 m為例，不同設計坡比下的邊坡塑性區分布見圖5。從圖5可以看出，雖然3種工況的塑性區均呈類圓弧形，并通過坡腳，但具體的塑性區形狀與位置存在一定差異。在坡比增大過程中，塑性區逐漸由深層向淺層發展，潛在滑動面也逐漸變窄，圓弧滑動面曲率不斷減小，形狀逐漸細長化。最大位移值也隨坡比增加而不斷變大，尤其是降雨入滲深度從4 m增加至5 m后，塑性分布區的位移顯著增加。

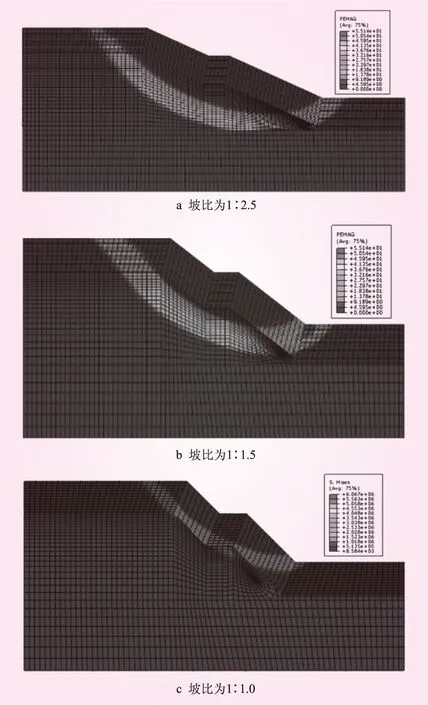
圖5 不同坡比邊坡穩定臨界塑性區

綜上，隨著降雨量持續增加，邊坡的降雨入滲深度也逐漸增加，導致邊坡的潛在滑動面由深部向淺層發展，邊坡穩定性不斷降低。此外，設計坡比也是影響邊坡穩定性的重要影響因素，坡比的設計值過大，使得開挖面的塑性分布區位移顯著增加。因此，在進行水利工程高邊坡的防護和加固時，應切實做好防水、排水的措施，并在重要工程中適當減小設計坡比。對存在安全隱患的水利工程高邊坡，更加應針對性采取邊坡防護和加固措施，從而有效抑制黃土邊坡受到降雨影響而產生滑動變形[15]。

4 結 語

本研究基于FLAC 2D仿真計算軟件，對黃土高邊坡在降雨入滲和設計坡比影響下的穩定性進行了分析，得到如下結論：

(1)基于FLAC 2D仿真計算軟件的邊坡穩定性分析對不同工況均具有較好的適用性，隨著降雨入滲深度、邊坡設計坡比的增加，邊坡的穩定性安全系數不斷減小。

(2)隨著降雨入滲深度的增加，邊坡位移場的塑性區不斷發展。在入滲深度從0增加到6 m過程中，潛在滑動面的位置逐漸向坡面發展；當入滲深度為6 m時，潛在滑動面基本貫通。

(3)隨著設計坡比增加，邊坡的整體塑性區形狀越來越細長，潛在滑動面的曲率有所減小，潛在滑動面位置逐漸由深部轉向淺層發展。

(4)為了提高邊坡穩定性，需要切實做好坡面的防、排水措施，并在重要工程中適當減小坡比。