壓差式光纖矢量水聽器聲壓相位靈敏度研究

張 滔，胡斌杰，陳超育，郭運動，鄧志儒，石 滔，徐 棟

(1.華南理工大學 電子與信息學院，廣東 廣州 510000;2.長沙深之瞳信息科技有限公司，湖南 長沙 410008)

0 引言

水聽器可分為標量水聽器和矢量水聽器。單個標量水聽器只能得到聲場的聲壓信息，不具備空間指向性。單個矢量水聽器不僅可測得聲場的聲壓，還可獲得聲場中的矢量信息，如聲壓梯度、質點振速等[1]。

光纖矢量水聽器按照其與聲場的相互作用方式可分為同振式和壓差式。同振式通過剛性幾何體內的傳感結構直接拾取外部介質質點振動信號；壓差式是利用空間距離很近的兩點處聲壓的有限差分來近似得到聲壓梯度[2]。

壓差式光纖矢量水聽器的測量與加速度無關，與同振式相比，其具有良好的抗加速度性能，可搭載在魚雷、潛航器等移動平臺上及組成拖曳陣等應用優勢[3]。開展壓差式光纖矢量水聽器研究，對海洋環境監測及維護海洋安全具有重要意義。

本文在聲-固耦合多物理場中對壓差式光纖水聽器進行仿真分析，并給出了工作頻帶內的聲壓靈敏度，且計算結果與實驗結果基本吻合。借助本文對壓差式光纖水聽器的仿真分析模式，可快速獲得一定條件下的最優性能設計，減少樣品試驗次數，節約研發費用，并顯著加快產品的研發進度。

1 光纖傳感器原理及模型仿真分析

壓差式光纖矢量水聽器采用雙干涉儀結構，每一個軸向由兩個光纖水聽器即基元構成，分別測量軸上兩個點的聲壓。基元聲壓傳感結構采用芯軸型推挽式結構，該結構易做到抗加速度性能，具有較高的諧振頻率[4]。同時，采用這種芯軸式推挽結構可以消除溫度、壓力等變化對光纖水聽器的影響。增敏結構采用空氣腔結構進行設計。具體結構由兩個帶肋骨薄壁圓柱殼體組成(見圖1)。

圖1 基元模型

光纖水聽器采用光相位調制原理(見圖2)。從激光器發出的光經耦合器分束后進入干涉儀的兩臂，即內外兩圓柱殼上纏繞的光纖；兩束光經光纖末端法拉第旋光鏡反射，回到耦合器進行干涉，形成調制信號[5]。光纖水聽器受聲壓作用，內、外兩個圓柱殼在徑向方向發生相反形變，進而引起纏繞在圓柱殼上的光纖一個伸長，另一個縮短，使兩者產生一定的光程差，從而在光纖干涉儀上引起相位變化。

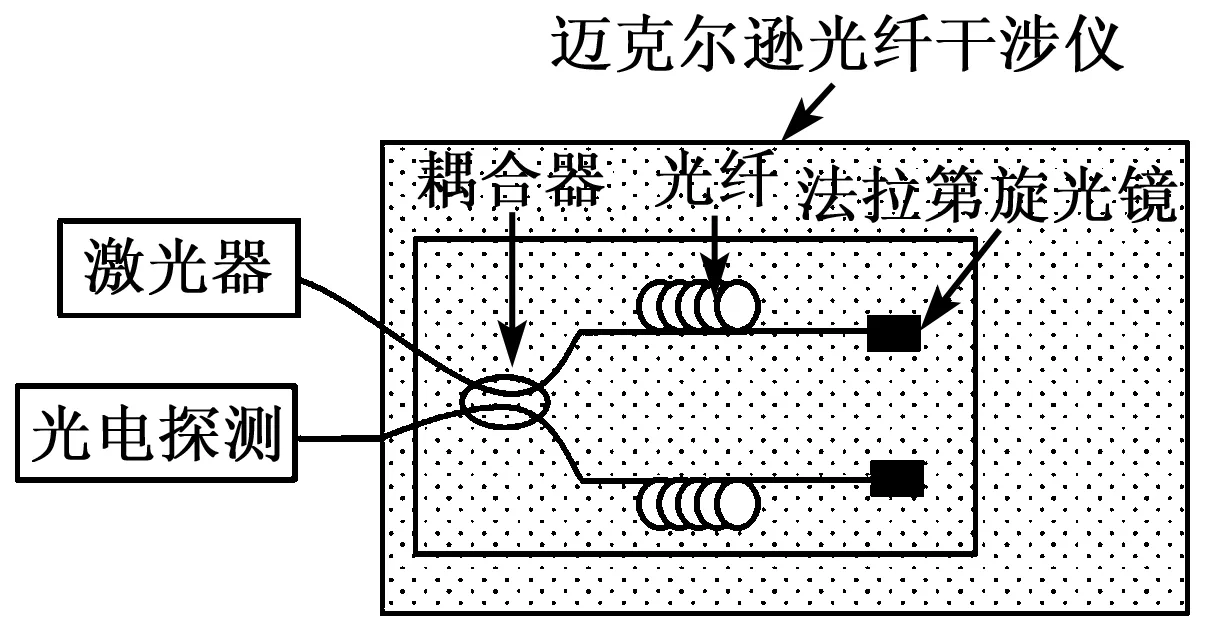
圖2 光纖傳感器原理圖

圓柱殼在聲壓作用下，承受軸對稱的均勻內壓，其徑向形變可由板殼理論來求解。圓柱殼光纖纏繞區兩端都有肋骨，肋骨厚度遠大于光纖纏繞區的壁厚，端部可近似為固支，則圓柱殼的平衡方程[5]為

(1)

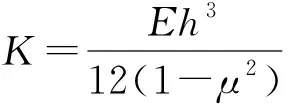
將坐標原點取在光纖纏繞區的中點，令α=βL/2，L為光纖纏繞區長度，求解式(1)可得圓柱殼軸向位置的徑向形變為

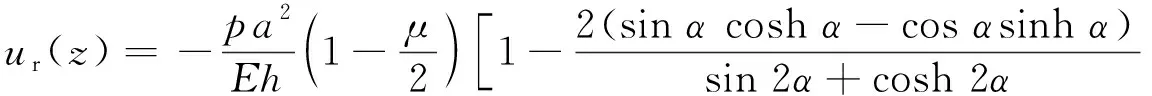
(2)

對圓柱殼受壓形變及光纖層等效處理進行仿真分析，并用式(2)的計算結果對仿真結果進行驗證。

hf=N×2πrf/4

(3)

式中rf為光纖半徑。根據直徑?160 μm光纖各層材料屬性，可得等效光纖層的楊氏模量Ef=18.72 GPa；等效泊松比μf=0.35。

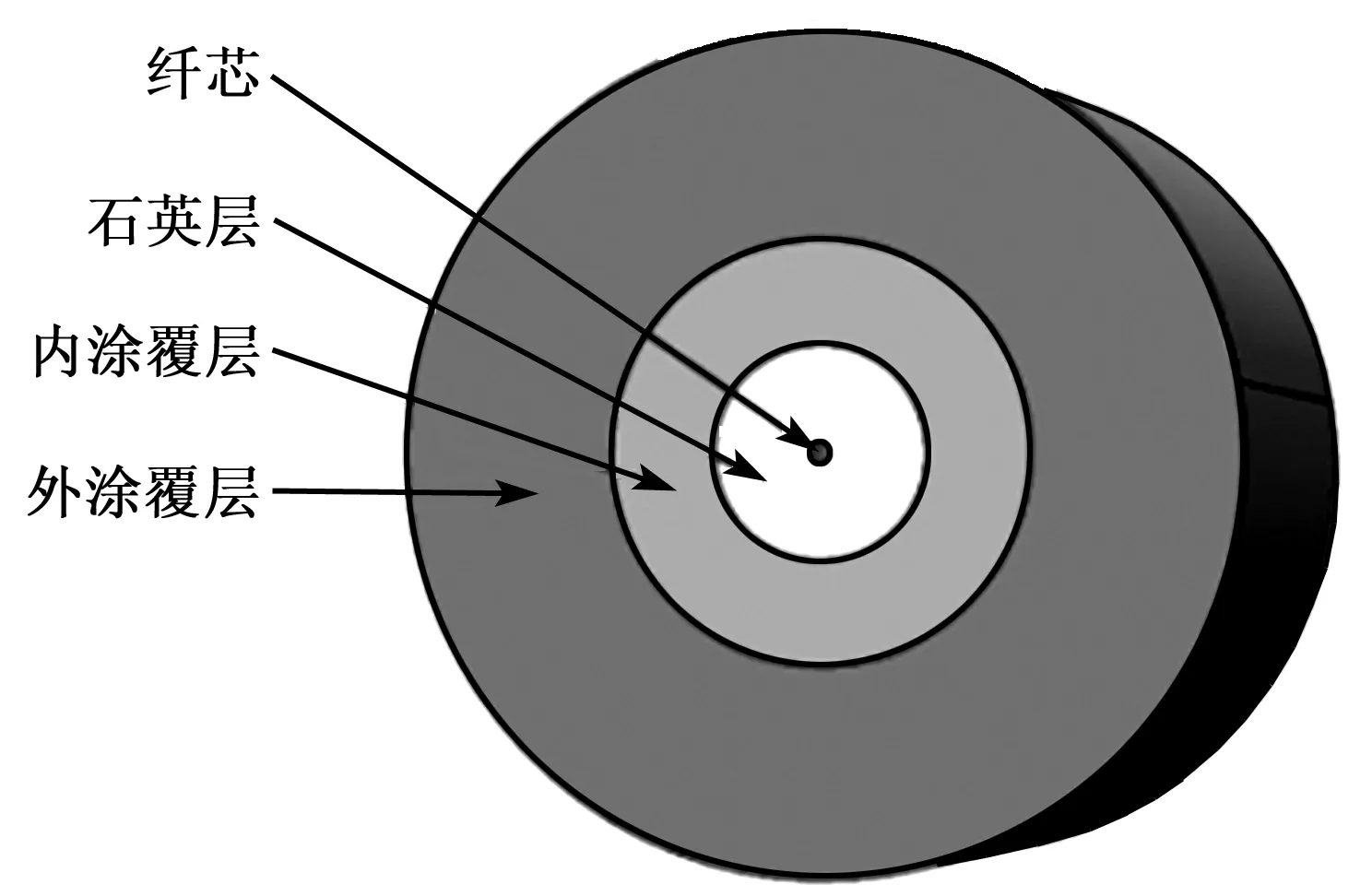
圖3 光纖橫截面示意圖

在COMSOL用二維軸對稱模型分析纏繞光纖層等效處理對受壓形變的影響。圓柱殼模型內半徑9 mm，長8 mm，壁厚0.3 mm，楊氏模量為70 GPa，泊松比為0.33，密度為2 700 kg/m3。再在圓柱殼上纏繞一層直徑?160 μm光纖。

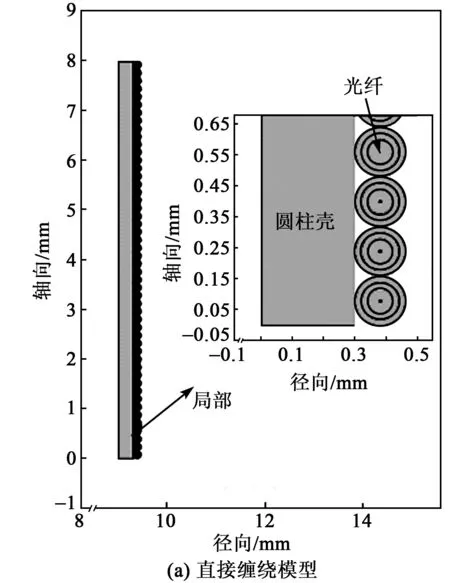
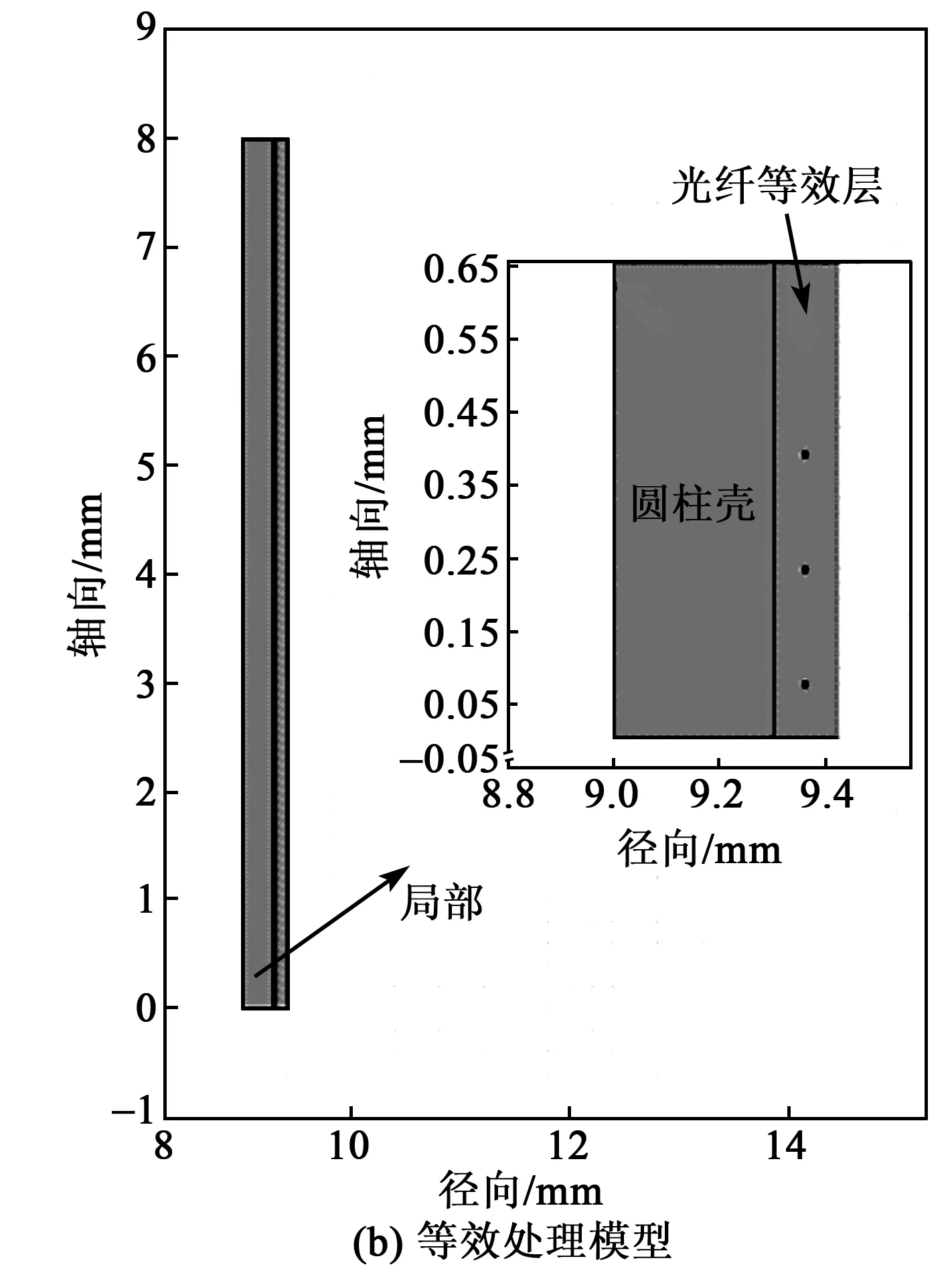
圖4 有限元分析模型

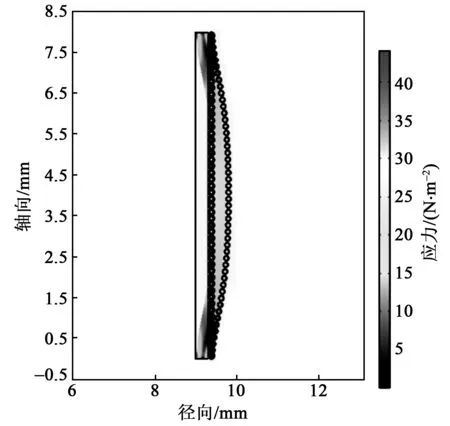
圖5 直接纏繞模型形變及應力分布

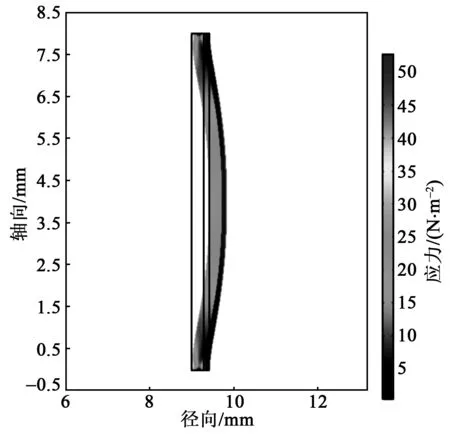
圖6 等效處理模型形變及應力分布

圖4為有限元分析模型。圖中的黑色點為計算徑向形變取點位置，每一匝光纖取一個點，圖4(a)、(b)取點位置一一對應。圖5、6分別為兩個模型的應力云圖。有限元仿真得到兩個模型每一匝光纖的徑向形變如圖7所示，同時基于式(2)給出了模型的理論形變結果。

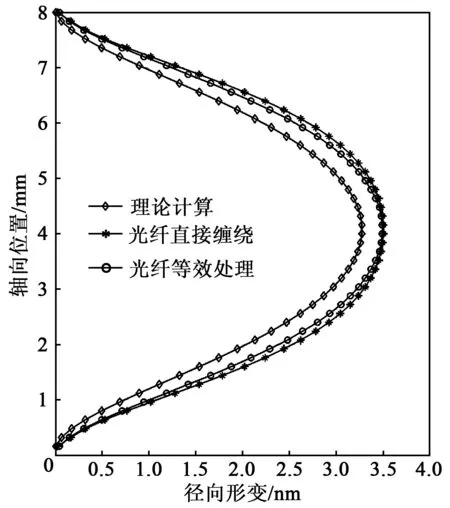
圖7 光纖層徑向形變對比

光纖傳感器聲壓相位靈敏度計算公式[7]：

(4)

(5)

式中：MP為聲壓相位靈敏度；Δφ為聲壓作用下引起的相位變化；P為聲壓；n為光纖纖芯折射率；Δl為光纖長度變化；λ為光源波長。

根據圖7所示形變結果和式(4)、(5)可算得光纖直接纏繞模型和光纖等效處理模型的MP=-163.7 dB和-164.0 dB，兩者差值很小。由此可見,對光纖層進行等效處理后再仿真，對計算結果影響不大。

將式(2)計算的形變代入式(4)、(5)，算得MP=-164.9 dB，即光纖水聽器的MP仿真結果與理論計算結果基本一致，差值約為1 dB。

2 壓差式光纖矢量水聽器仿真分析

壓差式光纖矢量水聽器在遠場平面波作用下的工作模型如圖8所示。

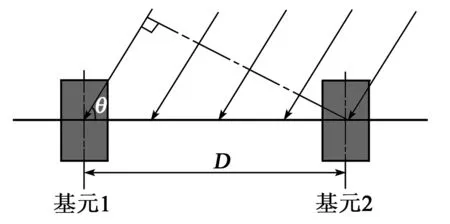
圖8 壓差式光纖矢量水聽器工作模型

壓差式光纖矢量水聽器聲壓相位靈敏度為

(6)

式中：PO為一維壓差式矢量水聽器聲中心聲壓，下標O表示軸的幾何中心;φ1和φ2為同軸的兩個基元在聲壓作用下產生的相位。

假設兩個傳感單元具有相同的MP，一維壓差式矢量水聽器[8]的M可表示為

(7)

式中：D為基元間距；k為聲波的波數;c為該介質下的聲速;ω為對應的角頻率;θ為入射波與傳感器夾角。

現選取一個目標模型進行仿真分析。模型要求取工作頻率f=1 000 Hz時，M≥140 dB，D=0.18 m。設計的基元模型參數如表1所示。根據表中給出的參數，在COMSOL軟件中搭建模型，并進行聲壓相位靈敏度仿真。

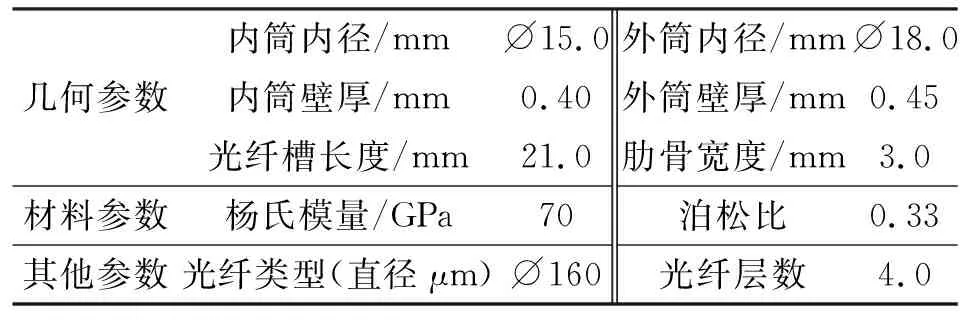
表1 基元參數

根據COMSOL軟件仿真計算得到光纖形變，即可求得在聲壓作用下的相位差，進而算得基元聲壓相位靈敏度。以內圓柱殼繞滿4層光纖計算得到基元聲壓相位靈敏度為-135.5 dB。在實驗測量中，基元樣品纏繞光纖長度要小于理想模型長度。基元樣品內圓柱殼纏繞光纖長為46 m、外圓柱殼纏繞光纖長為46.5 m；而理想模型內圓柱殼纏繞光纖長為52.8 m、外圓柱殼纏繞光纖長為53.3 m。根據實際情況，修正了基元模型，仿真得到聲壓相位靈敏度為-136.7 dB。基元樣品實測聲壓相位靈敏度為-137.2 dB。圖9為基元應力及形變。

圖9 基元應力及形變

在COMSOL軟件中物理場選擇‘聲-結構相互作用’，搭建模型并將兩個基元按間距D布置構成一個軸，置于水域中。再設置邊界條件模擬駐波管的聲場環境。圖10為有限元分析模型。在兩個基元聲壓作用下產生形變，通過形變計算，由兩者的相位差除以x(或y或z)軸聲中心處的聲壓，即可得到壓差式光纖矢量水聽器x(或y或z)軸的聲壓相位靈敏度。

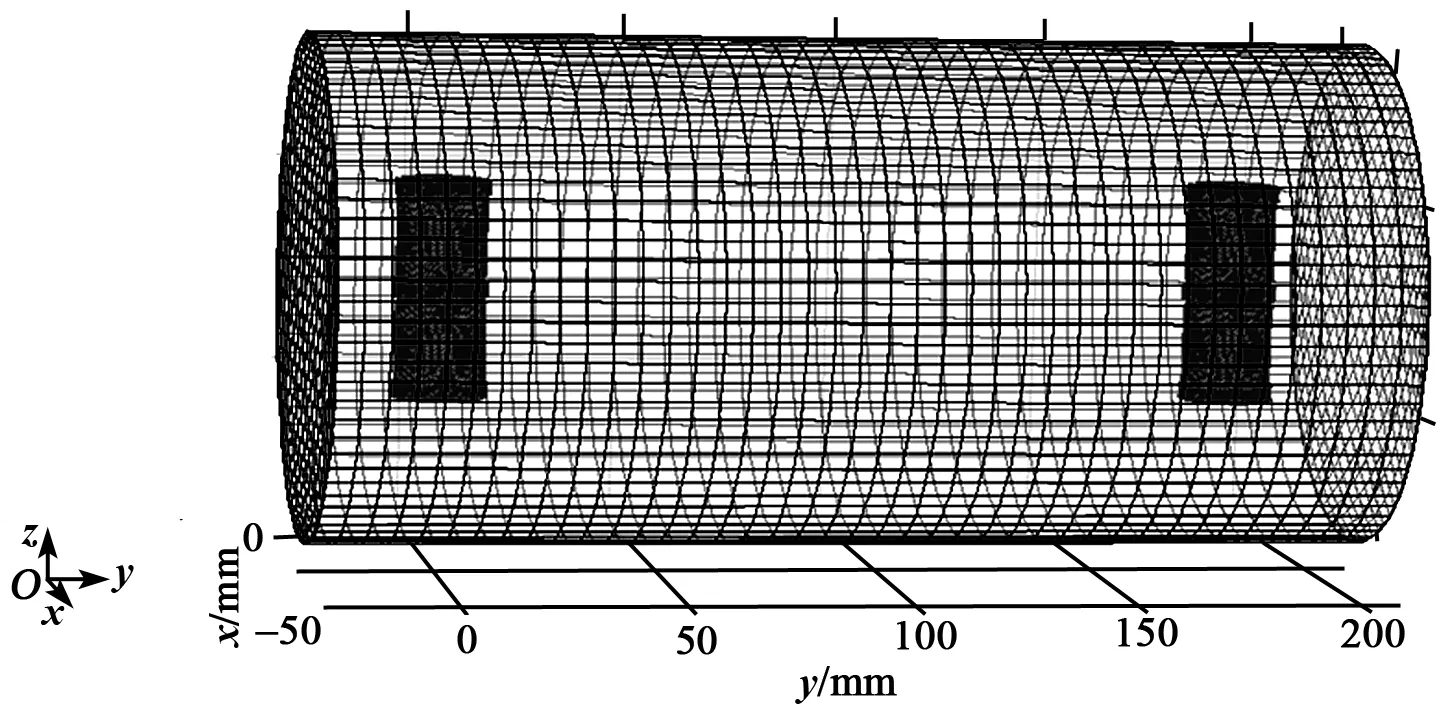
圖10 有限元分析模型

根據仿真計算結果，可以獲得不同頻率下的PO(見圖11)及由聲壓所引起的兩個基元的徑向形變(見圖12)，即得到纏繞在圓柱殼上的光纖長度變化。由光纖長度變化量可算得兩個基元的相位變化。將不同頻率的PO和基元相位差代入式(6)，得到壓差式光纖矢量水聽器聲壓相位靈敏度。仿真結果及參數如圖13和表2所示。

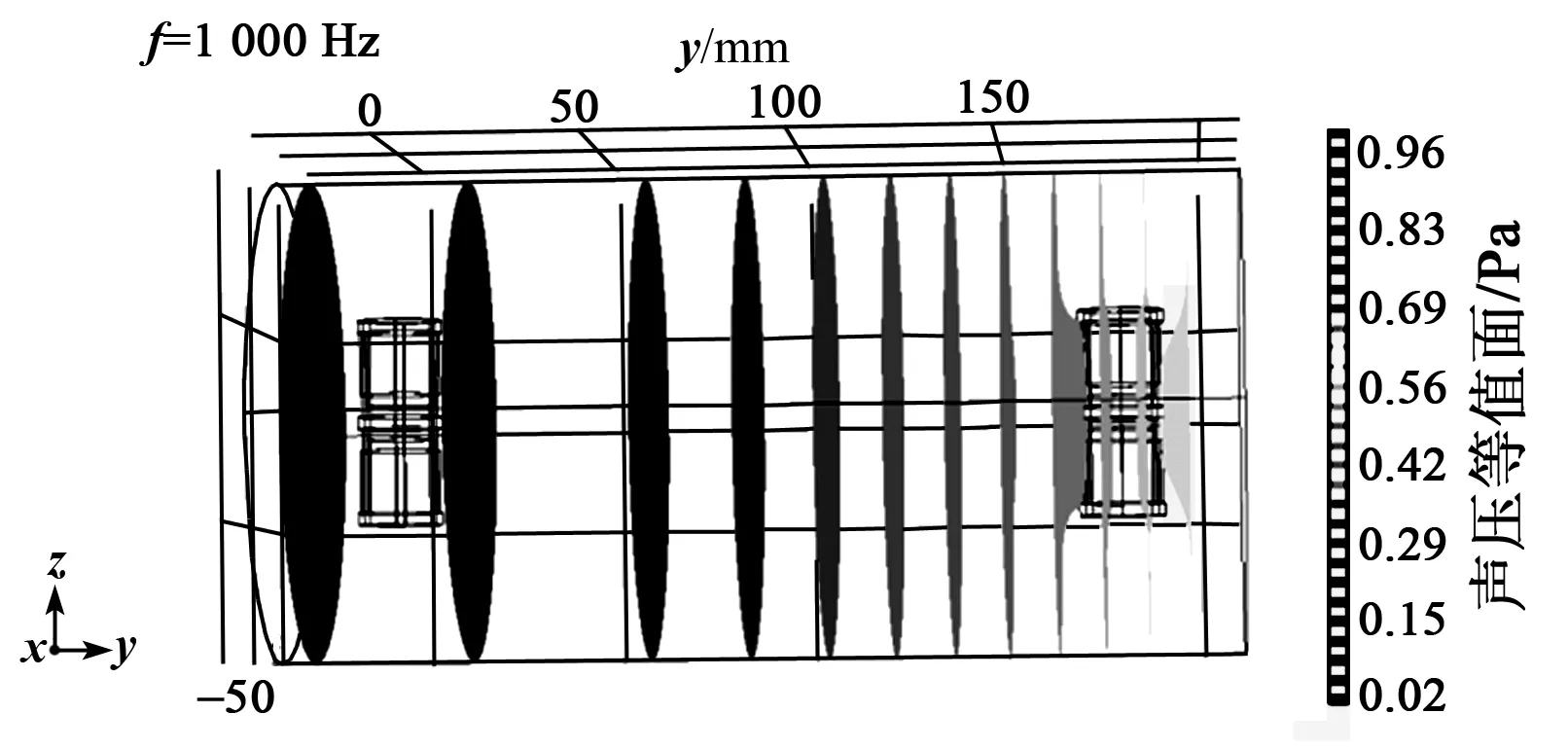
圖11 f=1 000 Hz時水聽器的聲壓分布

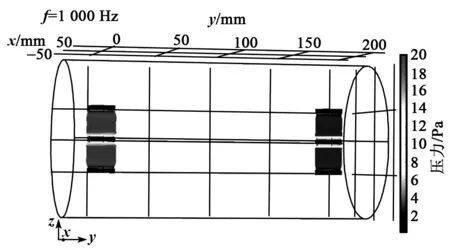
圖12 f=1 000 Hz時水聽器的應力及形變

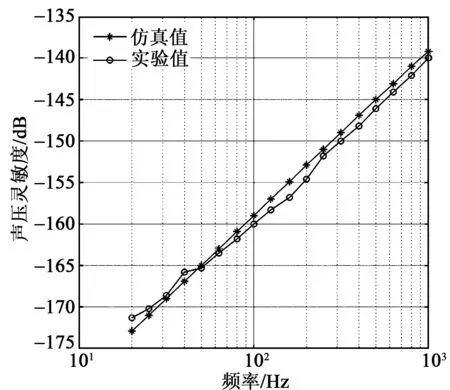
圖13 壓差式矢量光纖水聽器聲壓相位靈敏度

表2 壓差式光纖矢量水聽器光纖聲壓相位靈敏度

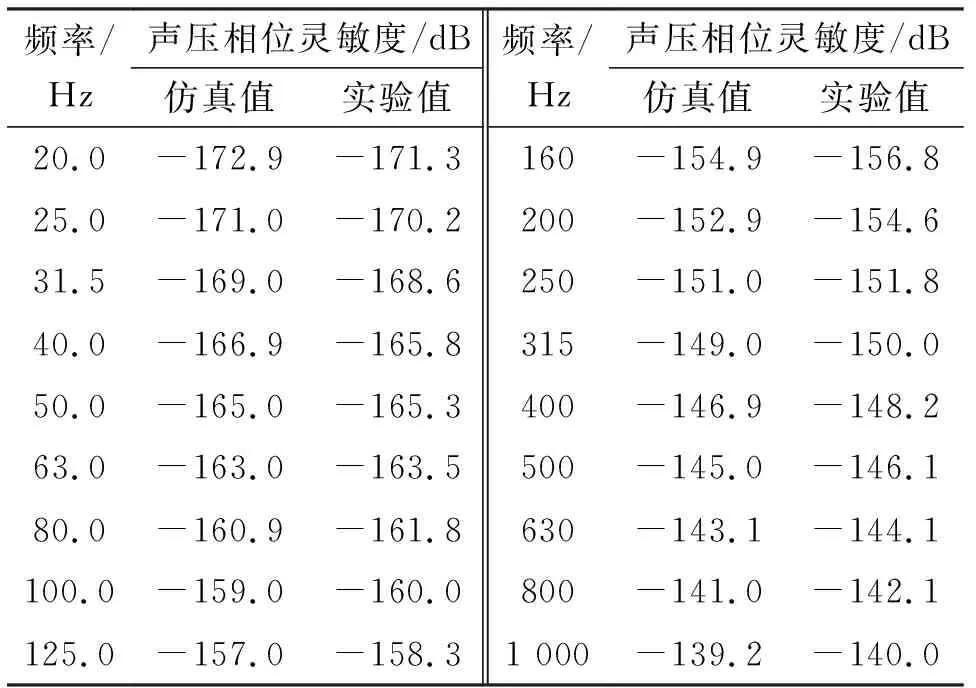
頻率/Hz聲壓相位靈敏度/dB仿真值實驗值頻率/Hz聲壓相位靈敏度/dB仿真值實驗值20.0-172.9-171.3160-154.9-156.825.0-171.0-170.2200-152.9-154.631.5-169.0-168.6250-151.0-151.840.0-166.9-165.8315-149.0-150.050.0-165.0-165.3400-146.9-148.263.0-163.0-163.5500-145.0-146.180.0-160.9-161.8630-143.1-144.1100.0-159.0-160.0800-141.0-142.1125.0-157.0-158.31 000-139.2-140.0

3 實驗

實驗室條件下校準矢量水聽器常采用駐波管法[9]，駐波管能獲得穩定的聲場，測試的不確定度相對較小[10]。為了對仿真結果進行驗證，根據以上仿真模型所選定的參數研制了一個壓差式光纖矢量水聽器樣品(見圖14)，并在駐波管中對其進行了測試。測試工作頻率為20～1 000 Hz，其測試結果如表2所示。由圖12及表2可知，壓差式光纖矢量水聽器聲壓相位靈敏度的仿真結果與實驗結果基本一致，平均差值約1.0 dB，僅在一兩個頻點出現較大偏差，最大偏差為1.9 dB。因此，在一定頻率范圍內，壓差式光纖矢量水聽器聲壓相位靈敏度仿真結果與實驗測試結果基本吻合，可作為設計參考依據。

圖14 壓差式光纖矢量水聽器及測試裝置

4 結束語

本文建立了壓差式光纖矢量水聽器有限元模型,并對模型的聲壓相位靈敏度進行了仿真分析，同時研制了壓差式光纖矢量水聽器樣品，并對其仿真分析結果進行了實驗驗證。研究結果表明，利用有限元法對壓差式光纖矢量水聽器的聲壓相位靈敏度性能進行仿真具有一定可行性。