一種基于壓縮感知的導波場重構方法
周 楊,駱 英,徐晨光,李鵬飛
(江蘇大學 國家級高端裝備關鍵結構健康管理國際聯合研究中心,江蘇 鎮江 212013)
0 引言
傳統導波檢測法常使用分布式傳感器陣列拾取損傷散射信號以定位損傷,此類方法可實現對結構損傷的快速定位,但受傳感器空間分布尺度的限制,難以獲取高空間分辨率波場[1-2],故而難以從采樣信號中獲取更多損傷信息。使用非接觸式掃描激光多普勒測振儀(SLDV)能夠獲得結構被測區域內高空間分辨率波場信號,并利用波場分析技術對損傷進行精確評估[3]。此處的“波場”指導波在被測結構中傳播及與結構特征相互作用的一系列隨時間或頻率演化的圖像,本文主要指時域演化圖像。受限于奈奎斯特(Nyquist)采樣定律,采集波場信號時,因空間采樣間隔須小于最小半波長,則導致測點數量龐大,測量完整波場的過程耗時過長[3]。近年來有學者利用壓縮感知(CS)技術[4-5],通過抖動采樣策略在采樣率遠低于Nyquist采樣率的條件下采集稀疏分布的測點信號,然后利用非線性重構算法恢復波場[6-7]。這些方法可對原始波場進行高精度重構,但均依賴抖動采樣策略,而抖動采樣具有隨機性,需在現有的商用SLDV系統上增加額外的控制組件,進而增加系統復雜度和成本。
針對上述問題,本文使用一種新的采樣策略,用均勻稀疏采樣網格替代隨機的空間測點坐標,以便SLDV實現稀疏采樣,并搭建PZT激勵/SLDV傳感實驗平臺,采集含損鋁板數據對該采樣方案進行驗證。本文所構建的基于SLDV均勻稀疏采樣的波場重構方案,既突破經典Nyquist采樣率的限制,又可方便SLDV測量系統執行空間稀疏采樣,研究結果可提高波場獲取效率。
1 基本理論
1.1 壓縮感知
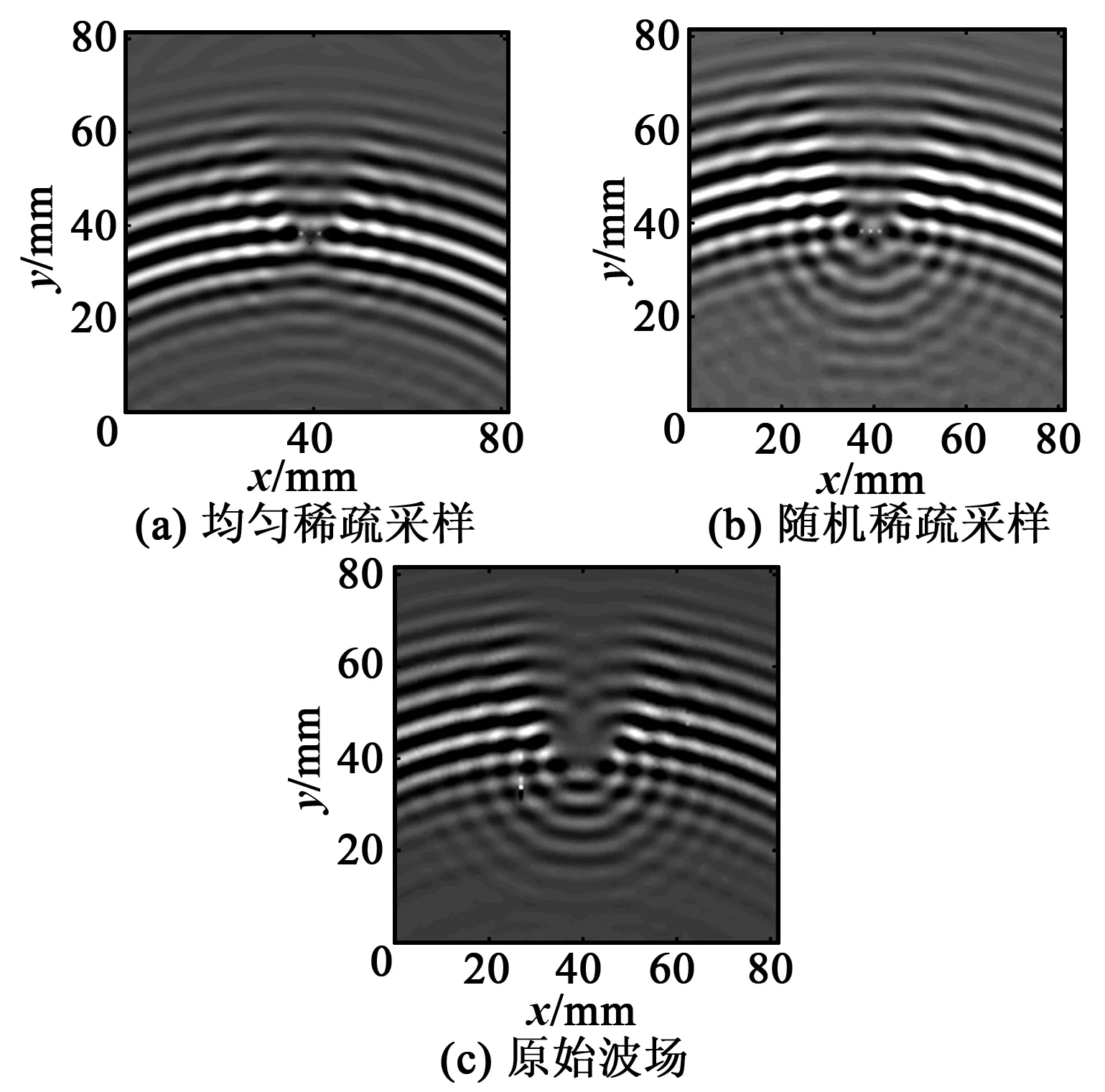
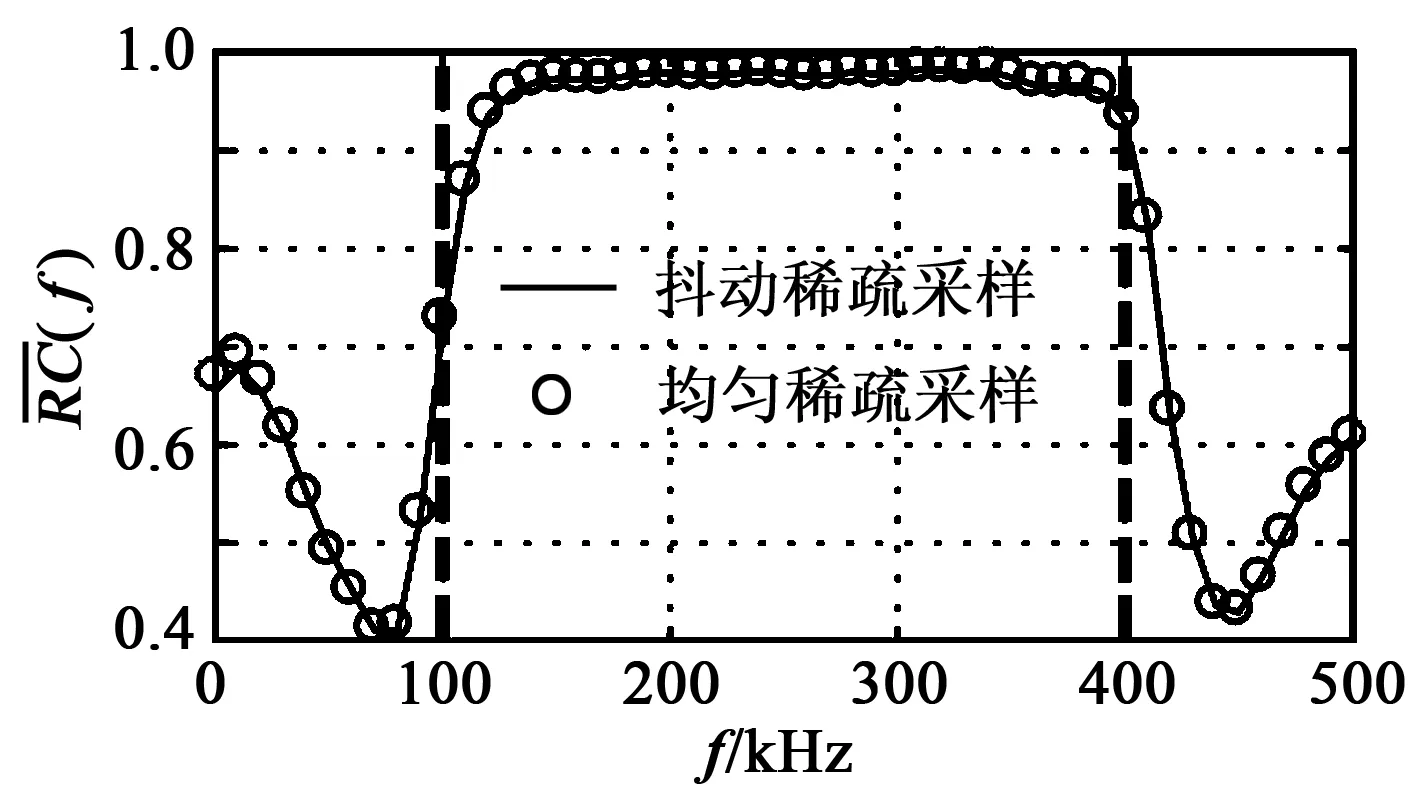
Nyquist采樣定律指出,為不失真地恢復模擬信號,采樣頻率須不低于模擬信號最高頻率的2倍,但該定律僅利用信號帶寬有限的假設,并未利用到其他與信號內在結構上相關的先驗知識。為突破Nyquist采樣定律的限制,Candès[4]、Donoho等[5]在21世紀初提出了CS理論。該理論針對稀疏信號或可壓縮信號通過隨機投影法進行了信號的壓縮采集,然后將測得的少量信號輸入到非線性求解器中恢復出原始信號。此處的稀疏信號指所包含的元素絕大部分等于0,僅含有少量非零元素的信號,而可壓縮信號指本身并不稀疏,但在某組已知基下存在稀疏表示的信號。CS理論研究的問題在數學上可描述為:設長度為N的一維稀疏信號x∈N×1(為實數集)的稀疏度為K,即x中僅含K個非零值,且K 若將待測結構的測量區域等間距地劃分為數個像素點,則在這些像素點中,位于結構特征(包括激勵源、預留孔及損傷等)附近的像素點個數是有限的。將這些像素點視作“假定源”,顯然真實源的存在具有相當高的稀疏性,圖1為二維測量區域像素化示意圖。 依據源的稀疏性可以構造CS方程。 圖1 二維測量區域像素化示意圖 (1) y(μ)(f)=A(μ)(f)v(μ)(f) (2) (3) 在多模態情況下仍可用相同的方式構造CS方程。本文采用較低的激勵頻率,使激勵源僅產生A0與S0模態導波,此時式(2)擴展為 A(f)v(f) (4) 式中A(f)為傳感矩陣。式(4)為最終的導波場CS方程。 求解CS方程的方法較多,由于基追蹤降噪算法在測量噪聲存在時具有較高的魯棒性,因此,本文擇其作為求解方法,具體使用屬于基追蹤降噪算法的譜投影梯度l1正則化算法包[8]。求解時需要將CS方程轉化為下述問題: (5) 式中σ為測量噪聲水平。當σ=0時表示無噪聲理想環境,σ越大表示噪聲強度越高。 基追蹤降噪算法在求解時需要傳感矩陣滿足一定的正交性,因此,采樣策略須兼顧隨機性與均勻性[7]。此處采樣策略包括了測點分布和假定源分布。現有研究利用抖動采樣法生成空間測點[6-7],假定源則為均勻分布,如圖2(a)所示。然而抖動采樣具有隨機性,現有商用SLDV系統內置的測量方式為均勻網格,并不支持隨機測點設置。本文將抖動采樣點替換為等間隔均勻采樣點以保證SLDV的稀疏采樣更易實現,采樣設置如圖2(b)所示。均勻稀疏采樣形成的傳感矩陣的冗余度高于抖動稀疏采樣,這是它們的本質區別。本文通過大量實驗數據計算證實,在傳感矩陣冗余度較高的情況下使用SPGL1算法求解導波場CS方程,能以非常高的概率求得滿足條件的稀疏解,因此,均勻稀疏采樣策略亦可精確重構出原始波場。 圖2 假定源與測點布置示意圖 利用假定源激勵函數的幅值信息可成像假定源區域的所有聲源,損傷作為二次聲源亦可被識別。由于SLDV測量系統直接測量的是結構表面的離面速度,因此,S0模態導波非常弱,A0模態在測量信號中占主導地位,利用v(f)中A0模態部分進行損傷成像,成像指標index(x,y)定義為 (6) 式中f1,f2為計算頻段的起止頻率。 利用假定源的激勵函數v(f)不僅可以成像損傷,還能對任意區域的波場進行重構。選定波場重構區域,構造假定源到該區域重構點之間的傳遞矩陣A′,可得該區域的頻譜波場: W(f)=A′(f)v(f) (7) 對W(f)進行逆傅里葉變換即得到任意時刻波場W(t)。 構建PZT激勵/SLDV傳感實驗平臺,如圖3所示。待測試件為厚1 mm的T6061型鋁板,如圖4所示。在鋁板表面粘貼直徑為7 mm的壓電片作激勵源,在激勵源上方設置長10 mm的凹槽模擬損傷。測量區域寬、高均為81.5 mm,M=221,在每個測點上采集10次數據后取均值以提高信噪比。假定源區域寬81.5 mm,高180 mm,假定源點數N=2 695,等于取該區域Nyquist點數,采樣壓縮率為(1-M/N)×100%=91.8%,即實際采樣點數減少至Nyquist點數的8.2%。激勵信號為中心頻率250 kHz的五峰波,信號能量主要集中在100~400 kHz,故選擇該區間作為計算頻段。 圖3 PZT激勵/SLDV傳感實驗平臺示意圖 圖4 待測鋁板試件示意圖 2.2.1 損傷成像 圖5為基于均勻稀疏采樣與基于抖動稀疏采樣策略計算得到的損傷成像。表1為損傷中心位置估計結果。由表可知,兩者的定位誤差均能控制在最小半波長以內,前者的定位誤差略低于后者。以損傷成像的最大長度來估計損傷最大尺寸,得到如表2所示的結果。由表2可知,兩種采樣方案在損傷尺寸估計精度上處于同等水平,估計值均略小于最小半波長。上述結果表明,均勻稀疏采樣策略具有較高的損傷成像和定位精度。 圖5 損傷成像結果 表1 損傷定位估計 真實位置/mm估計位置/mm絕對誤差/mm均勻稀疏采樣隨機稀疏采樣(40,45)(40.0,44.1)1.1(40.0,44.2)1.2 表2 損傷最大尺寸估計 2.2.2 波場重構 (8) 圖6 重構波場與原始波場 圖曲線 本文提出了一種基于均勻稀疏采樣策略的導波場稀疏重構與損傷成像方法,并搭建PZT激勵/SLDV傳感平臺在含損傷鋁板試件上進行了實驗驗證。結果表明,本文所提出的方法在損傷成像、定位和波場重構方面均能達到與既有的基于抖動采樣策略方法同等的精度,可將獲取全導波場的空間測點數降到傳統Nyquist采樣點數的10%以下,且均勻稀疏采樣能使SLDV在采集數據時更便捷,進而可極大地提高導波場分析法的實用性和工作效率。1.2 導波場中CS方程的構建
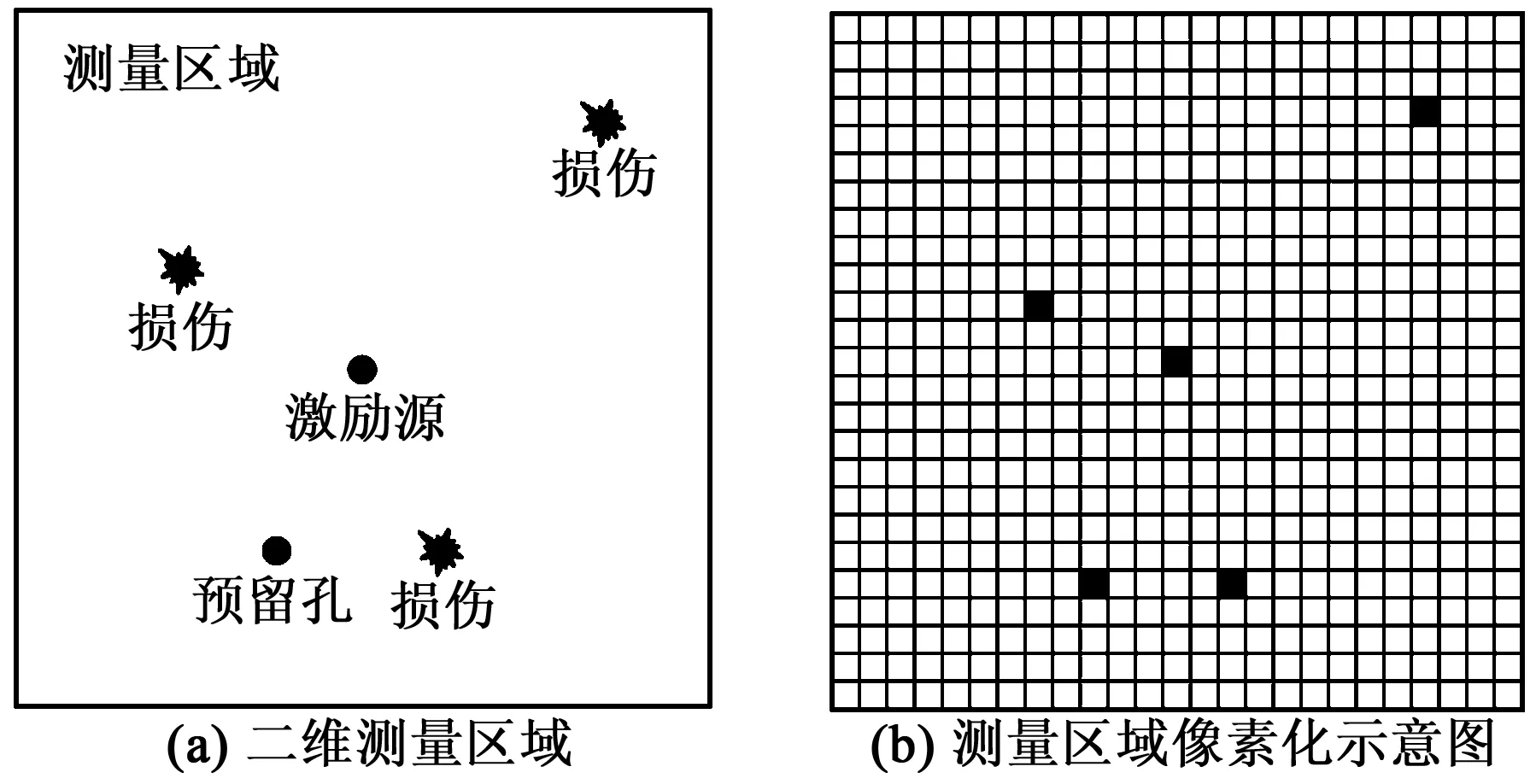
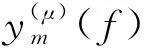
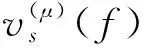
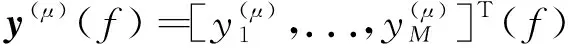
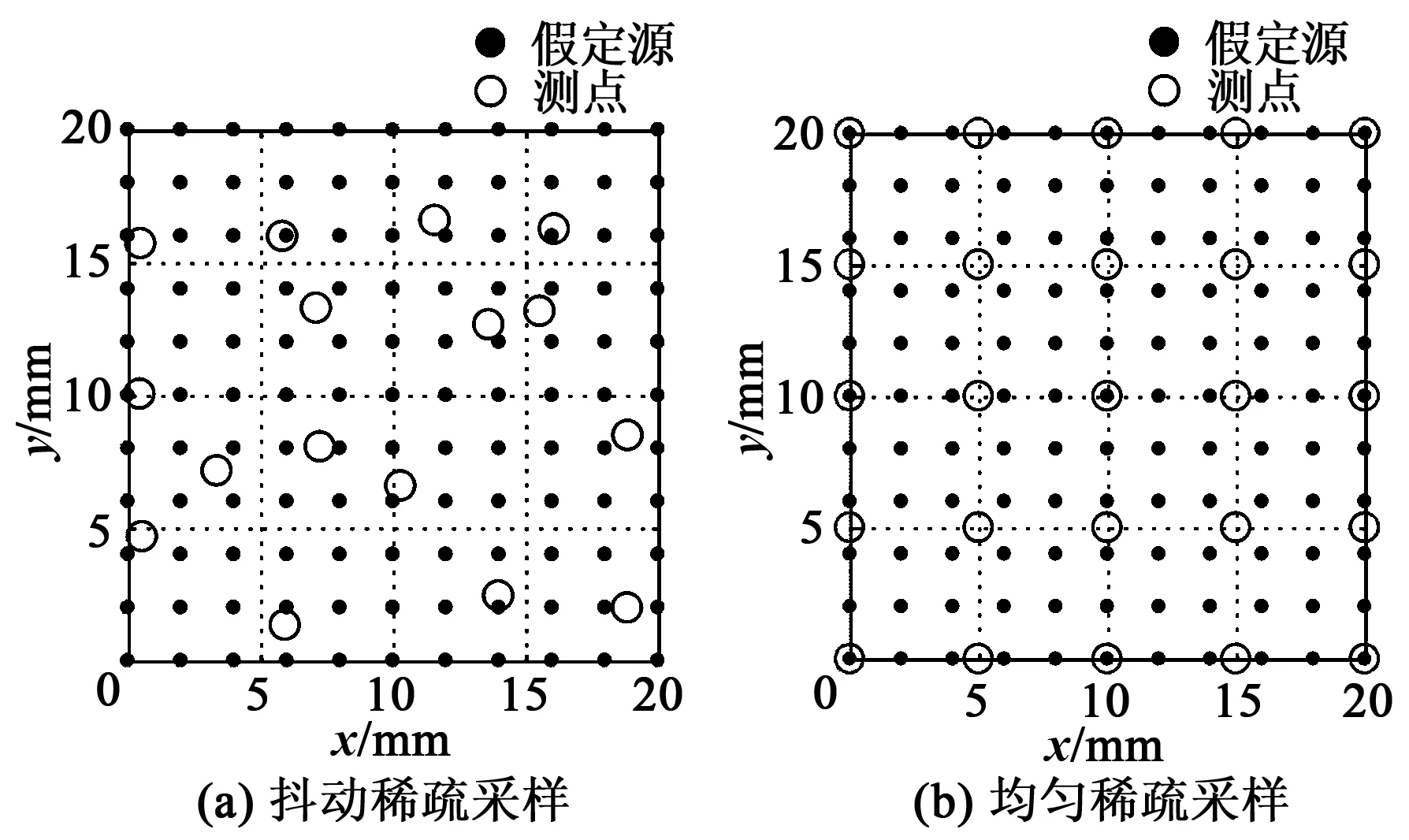
2 實驗驗證
2.1 實驗設置
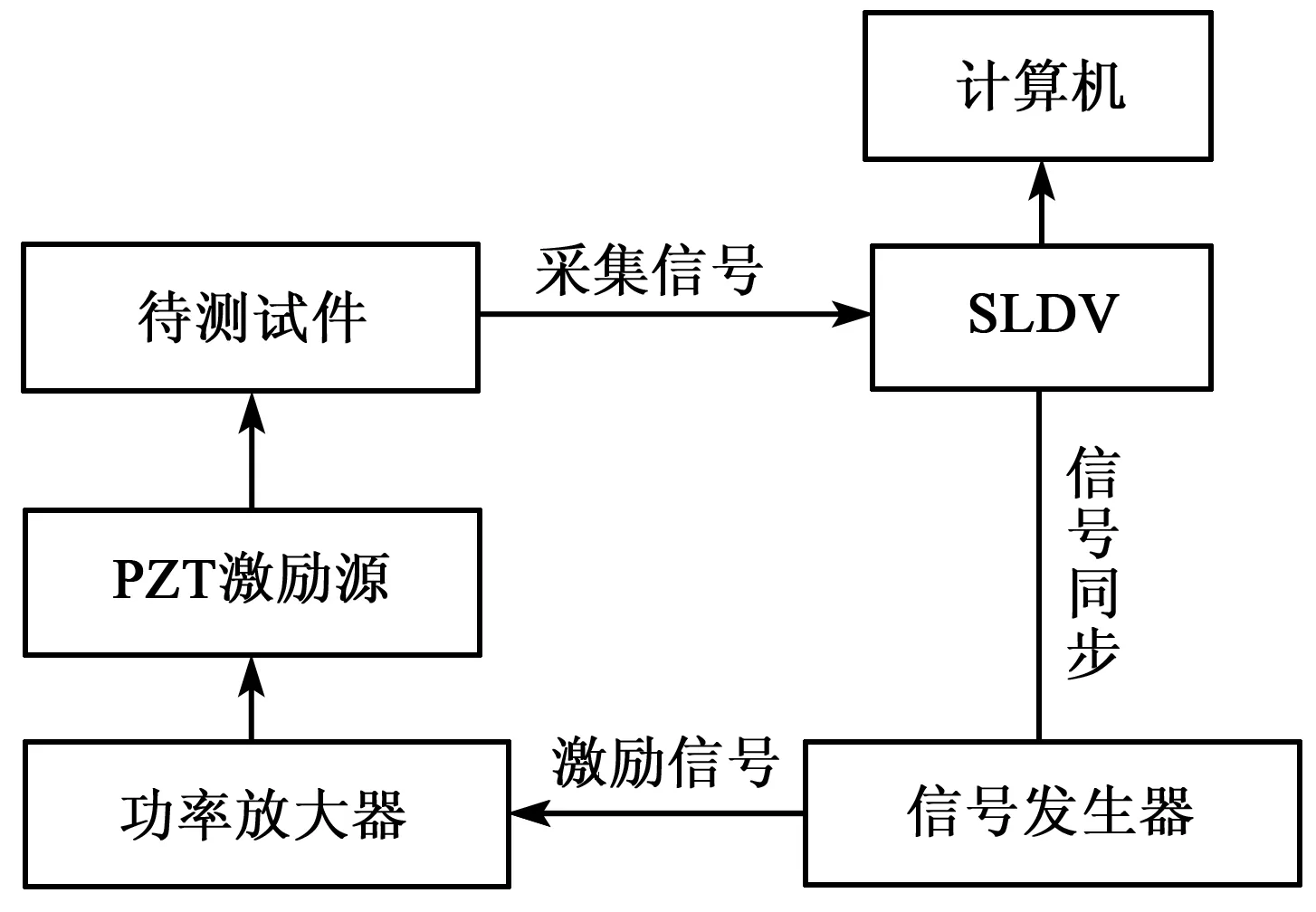
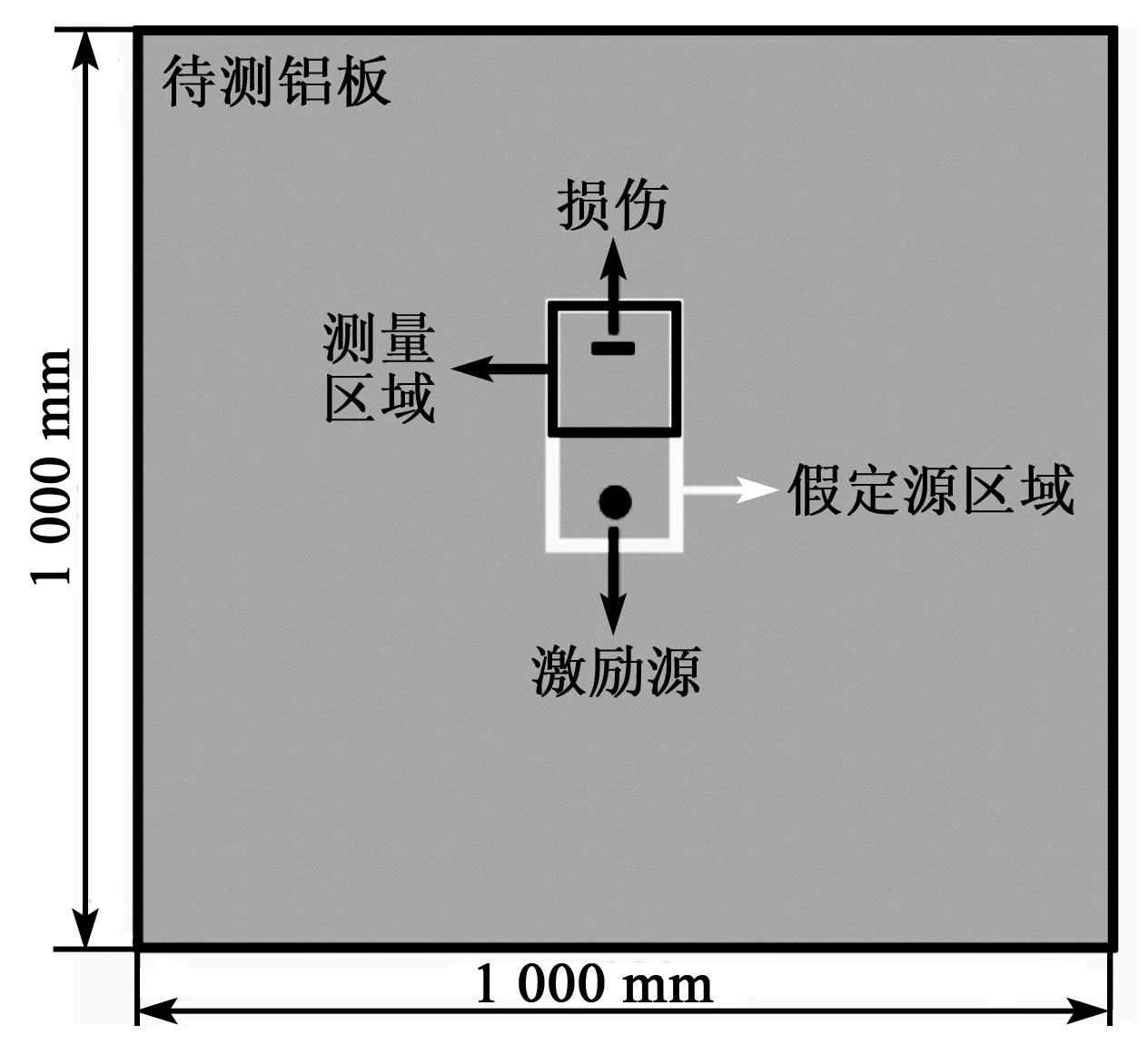
2.2 實驗結果



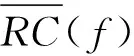
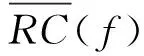
3 結束語

