雙H叉合式定子諧振驅動的壓電平面電機研究

賀紅林，鄧傳濤，龍玉繁，胡聰睿，冷新龍

(1.南昌航空大學 航空制造工程學院, 江西 南昌 330063；2.江西洪都國際機電有限責任公司，江西 南昌 330063)

0 引言

壓電電機是基于逆壓電效應實現機電動力轉換的新型電動機，具有動力密度大，響應快，運動精密，結構靈活及噪聲小等優點，在航空航天、精密加工、生物醫學工程等領域具有廣闊的應用前景[1-3]。壓電電機有旋轉型、直線運動型、平面運動型、多自由度型等多種型式。目前，旋轉型超聲電機已漸成熟，其中的部分技術和產品如行波超聲電機技術已實現了產業化并在嫦娥號航天器等高精尖場合得到了應用。直線型電機技術的發展雖然落后于旋轉型壓電電機，但也推出了數十種的壓電直線電機，且有些電機如V型直線電機已達到產品化應用水平[4]。與旋轉型和直線型電機相比，平面型壓電電機的起步時間較晚且發展速度也較緩慢，因此，壓電平面電機技術離廣泛的工程應用還較遠。但平面超聲電機仍因運動方式靈活、應用前景廣而受到越來越多的重視。根據平面電機的運動特性并結合壓電驅動的精密性，平面電機將在大集成度微電子制造、光纖對接、微裝配、掃描隧道顯微鏡、能束加工、細胞編排、光學工程、遺傳工程、超精加工與檢測領域得到廣泛應用。因此，研究壓電平面電機就變得有意義，國內外為此做了不少工作[5-9]，如時運來研制出柱桿平面電機，劉潤峰[10]研制出口字型平面超聲電機；肖智勇研制出基于H臥板的平面電機；王京山等[11]提出了十字正交縱彎夾心換能器驅動平面電機。從已有研究來看，目前平面電機雖得到一定發展但其原理、結構和型式還較缺乏，且其性能還遠不能滿足應用對其提出的高精、高速、高加速和大動力等多種需求，故深入探索這類電機原理和結構成為其研究的重要內容。針對此背景，本文提出利用雙H叉合式同型模態驅動的平面電機，該電機結構簡單，動力學特性較好，有望輸出較大速度與動力。

1 定子結構及其工作模態

1.1 定子結構選型原則

根據壓電電機設計要求并結合平面電機二/三自由度運動的需求，不難梳理出壓電平面電機的定子結構設計的原則：

1) 定子宜采用中心對稱結構。這是因為如果定子結構過于復雜，則很難從結構稟賦的模態中找到所需工作振型，同時也不利于工作模態的激發。

2) 定子的結構拓撲應使其各工作模態的頻率天然地較接近，因此，定子設計時只需適度地調整其構型與尺度，便可在不引起工作模態畸變的前提下，實現工作模態頻率的一致性。

3) 定子結構方案的確定應有利于工作模態的高效激發，且應能保證當對工作模態進行正常激勵時，定子的驅動足能復合出微米級幅度的橢圓軌跡。

4) 定子結構拓撲應保證其驅動足能推動動子做兩相以上自由度驅動，且應避免各驅動足在推動動子時出現相互阻滯現象。

5) 定子結構拓撲及其工作模態的選擇應便于定子的夾持固定，且應保證定子固定后不會導致工作模態振型產生畸變及模態頻率出現大幅漂移。

1.2 定子的結構拓撲

根據上述原則并基于TRIZ理論，提出一種適于平面運動驅動的雙H叉合式(見圖1)，該定子由上、下、左、右4根外圍桿及一個十字板架組成，圖中，為增強各桿的柔性以利增大其彎曲工作振幅，在各桿的截面中心處均制出通孔，并且通過微調這些孔的尺寸，還可調整定子工作模態頻率，從而有利于實現工作模態頻率的一致性。為使各桿產生純正的面內、外工作彎振，在各桿與十字板架連接處開設了小槽口及在各桿中部位置開設小孔。小槽口的開設可緩解定子結構的應力集中，從而有利于提高其疲勞壽命。

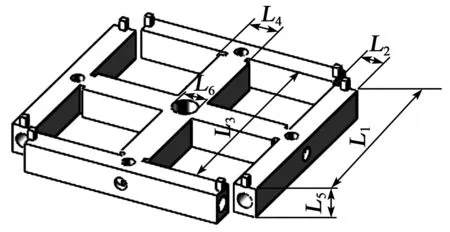
圖1 雙H叉合式定子的示意圖

1.3 工作模態假設

基于雙H叉合式的軸對稱幾何特征，并考慮到結構作工作模態振動時必須滿足動量守恒定律的原則，可推測雙H叉合式彈性結構稟賦的左(右)桿面內彎振、上(下)桿面內彎振及面外對稱彎振等模態(見圖2)，這3種模態的振型較清晰簡單，均具有利用壓電陶瓷進行激發的可能性。如果定子確實存在這些模態，則有望利用它們推進動子做平面運動。

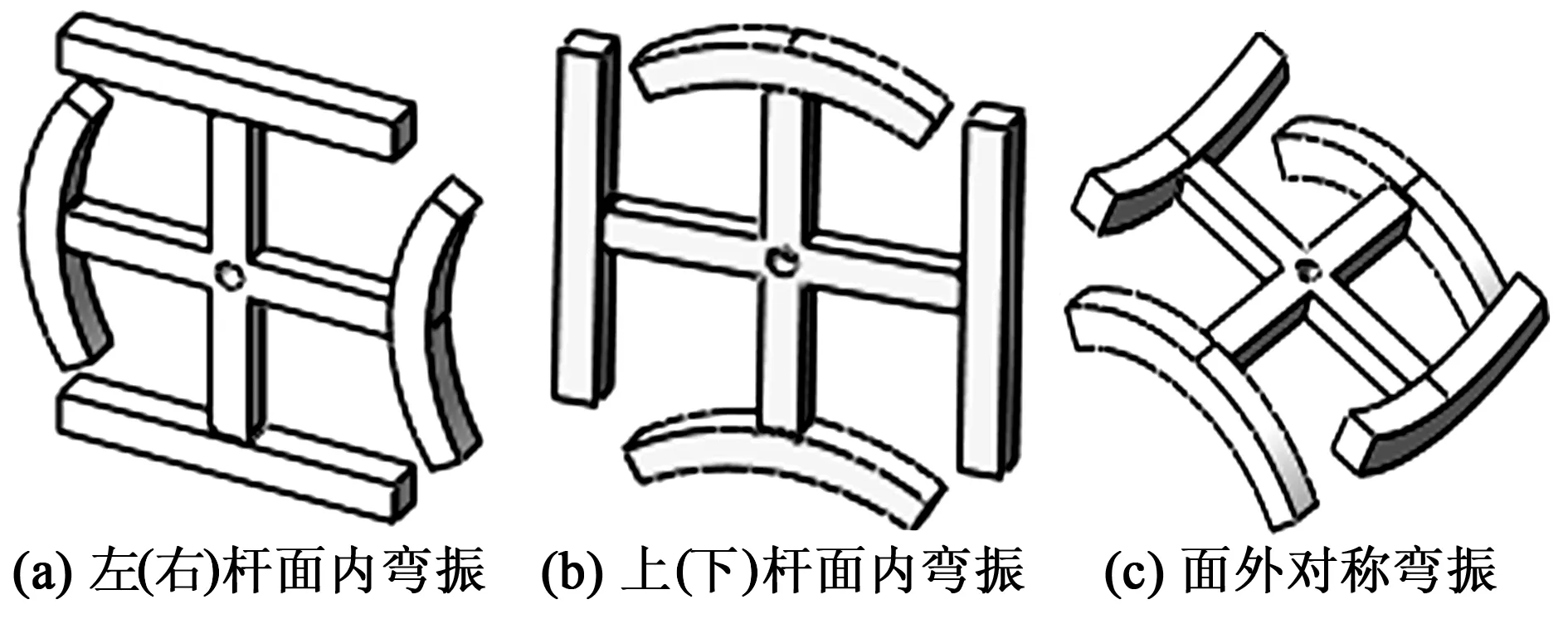
圖2 雙H叉合式定子的假設模態

1.4 工作模態確認

為驗證雙H叉合結構是否存在上述模態，本文根據壓電電機設計理論初擬了定子結構尺寸，并基于ANSYS軟件建立了定子動力學特性分析有限元模型，再借助該軟件的模態求解功能，且采用蘭索斯(lancoz)法提取到雙H叉合式定子振動模態如圖3所示。將圖2和圖3進行對比可知，兩者的振型很相近，這說明雙H叉合結構確實存在預設工作模態。仔細觀察求得的模態時，還發現這三相模態的振型均較純正，且它們的階次、頻率、振幅等均較接近，具有實現頻率一致的可能性。故本文確定將這些模態當作電機工作模態。

圖3 雙H叉合結構的計算工作模態

2 壓電極化配置與驅動足設置

定子的模態諧振是建立在壓電陶瓷片合理配置的基礎上，唯有對陶瓷片進行正確的極化并通入適當的驅動電壓，工作模態才能有效激發。壓電陶瓷布片、極化及供電對于有效地激發模態振動、簡化電路的設計、提高機電轉換效率意義重大。壓電配置主要包括兩個方面，即

1) 陶瓷片極化與供電模式設計決定了模態的可激發性。

2) 陶瓷片位置確定決定了模態振動的效能。陶瓷片布片數量及壓電極化供電方案主要根據工作模態振型進行確定，而陶瓷布片及驅動足布設位置則取決于定子的模態應變與模態位移分布。大量的研究表明，在滿足貼片工藝的條件下，應盡量將陶瓷片布置在工作模態最大應變處；同時，為了在驅動足上獲得盡可能大的工作振幅，應將驅動足盡可能布置在工作模態振型的最大模態位移處。

可見，為優化陶瓷片及驅動足的位置，須先確定外圍桿的模態應變與模態位移分布。考慮到4根外圍桿的工作振動完全相同，故取左桿為對象并利用ANSYS求得模態位移與模態應變沿桿長的分布如圖4所示。由圖可知，該桿的最大模態應變處于桿中部，故理論上應將陶瓷片粘貼于該處，但考慮到在該處貼陶瓷片會明顯增大桿的彎曲剛度且在該處只能粘貼單片面內彎振激勵陶瓷片，從而不利于提高面內彎振激勵，故本文將陶瓷片貼在靠近中部的兩側位置。圖4還表明，最大模態位移出現在桿的兩端，為此將驅動足配置在桿的端部以便得到盡可能大的驅動足振幅。為保證定子工作時驅動足能與動子接觸并避免陶瓷片接觸到動子，設計驅動足時還令其高度遠大于壓電陶瓷片厚度，圖5(a)為陶瓷片及驅動足配置，圖中為定子配置了32片陶瓷和8個驅動足。

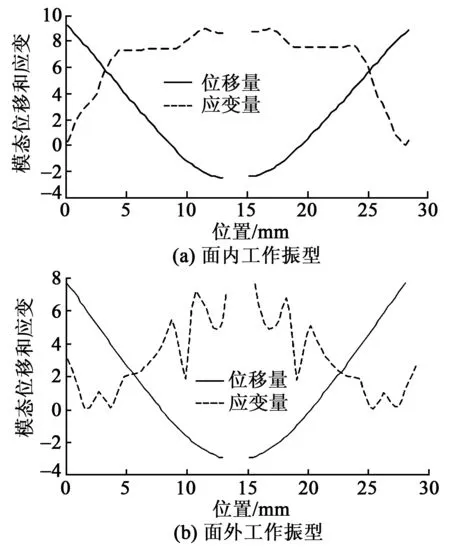
圖4 雙H叉合式定子的模態位移與應變分布

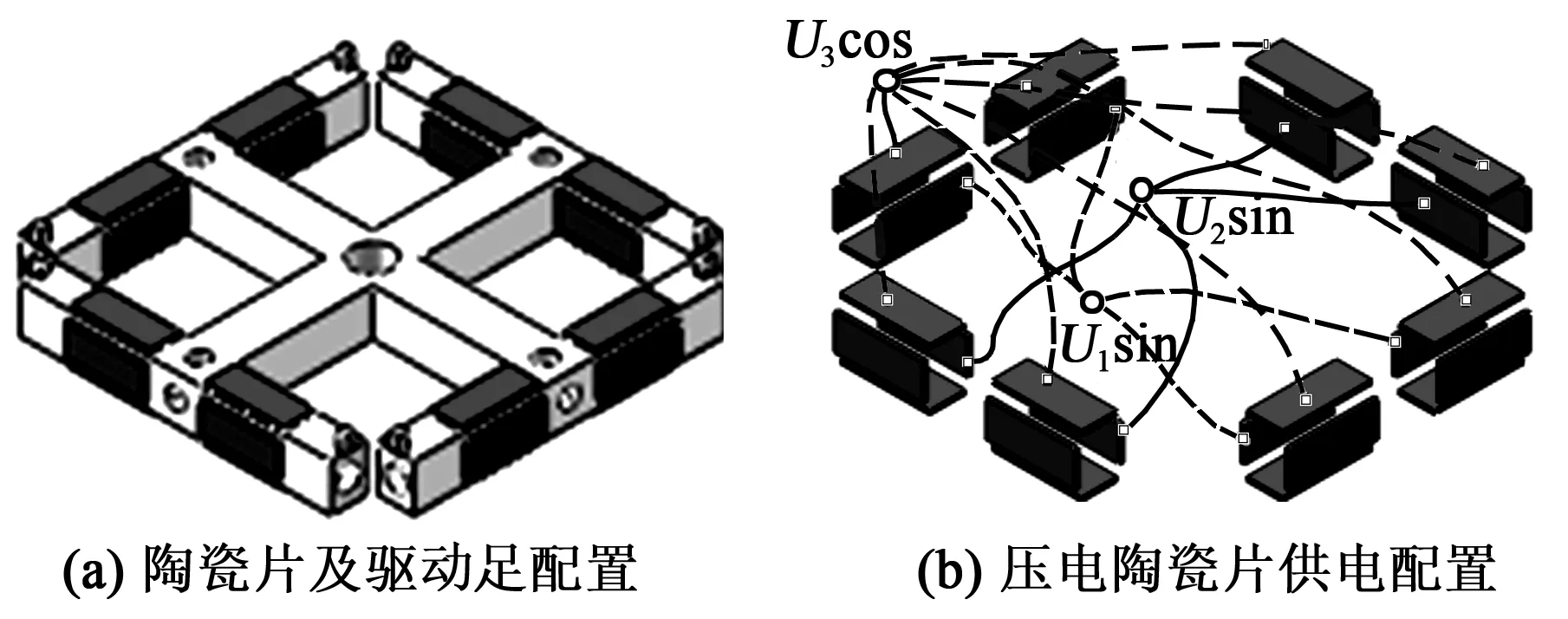
圖5 壓電陶瓷及其供電配置方案

本文令各陶瓷片均沿指向定子基體的方向進行極化。圖5(b)為壓電陶瓷片的供電方案。考慮到各桿外側和下表面處陶瓷片的供電分別與內側及上表面處陶瓷片的供電完全相同，故在圖中只給出了桿的內側及上表面處陶瓷片的供電。值得一提的是，為避免通電后出現電學短路，供電設計中還令各陶瓷片與定子接觸的電極均進行接地。

3 電機諧振驅動機理

本文的電機利用雙H叉合式定子面外彎振模態振動與左(右)桿面內彎振模態的諧振耦合，在左(右)桿的驅動足上復合出沿xz面行進的橢圓軌跡，并據此推進動子的x向滑移；通過面外彎振模態與上(下)桿面內模態諧振耦合，在上(下)桿的驅動足上復合出沿yz面行進的橢圓以推動動子的y向運動。驅動足的x、y向振動用以實現動子前移，z向振動實現驅動足與動子的瞬態接觸與分離。圖6為定子在一個振動周期T內推送動子的狀態。考慮到左、右桿的推送及上、下桿推送情況相同，故以右桿與上桿為例說明電機的驅動機理，即

1) 0～T/4時段。沿xz面，右桿由最大上彎態彎回到面外零彎曲變形量狀態，使其驅動足保持與動子接觸；而在沿yz面內，右桿由面內零彎曲量狀態彎成最大右彎態，使右桿上的驅動足A、B分別由A1、B1行至A2、B2并推動動子沿x向前移一步。與此同時，沿xz面，上桿由最大前彎態恢復到面外零彎曲量狀態，使上桿驅動足與動子分離；沿yz面，上桿由面內零彎曲變形量狀態彎成最大上彎狀態，使其驅動足E、F分別由E1、F1行至E2、F2。

2)T/4～T/2時段。沿xz面，右桿由面外零彎態彎成最大后彎態，使其驅動足與動子分離；而yz面，右桿由最大右彎態回復到面內零彎態，并使其兩驅動足分別由A2、B2到達A3、B3。與此同時，在xz面，上桿由面外零彎態向前彎曲至最大前彎態，使上桿的驅動足與動子接觸；在yz面，上桿由面內最大上彎態向下彎曲成面內零彎態，使上桿上的兩驅動足行至E3、F3并推動動子沿y向行進一步。

3) 在T/2～3T/4時段。沿xz面，右桿由最大后彎態彎回到面外零彎態，使其驅動足與動子仍不接觸；沿yz面，右桿由面內零彎態彎成最大左彎態，使其上的兩個驅動足分別由A3、B3到達A4、B4。與此同時，在xz面，上桿則由最大上彎態回復到面外零彎態，使上桿的驅動足仍保持與動子接觸；沿yz面，上桿由面內零彎向下彎曲成最大下彎態，驅使上桿的驅動足由E3、F3行至E4、F4并推動動子沿y向再移一步。

4) 在3T/4～T時段。沿xz面，右桿由面外零彎態向上彎成最大前彎態，使其兩驅動足與動子接觸；沿yz面內，右桿由面內最大左彎態回復到面內零彎態，使其驅動足分別由A4、B4到達A1、B1，并推動動子沿x向再移進一步。與此同時，在xz面，上桿由面外零彎態向后彎成最大后彎態，使上桿的驅動足與動子分離；沿yz面，上桿由最大下彎態彎回到面內零彎態，使上桿驅動足由E4、F4行至E1、F1。

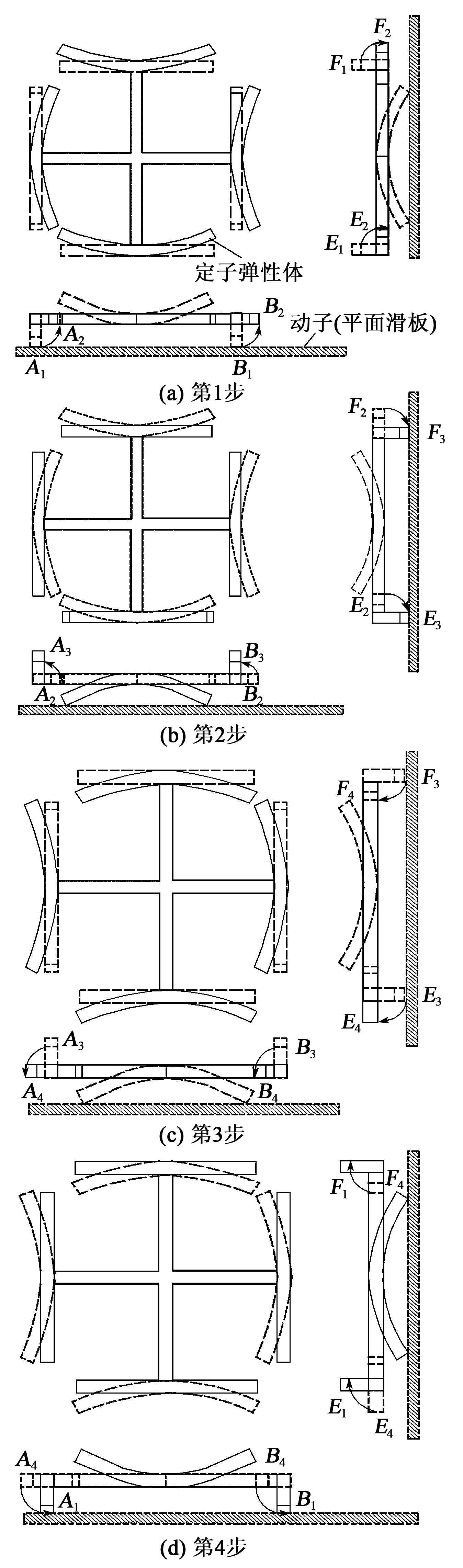
圖6 雙H叉合式定子推送動子的過程

定子每完成一個振動周期，驅動足分別沿x、y向推送動子移進2個步距，當定子不斷重復上述振動循環時就將推動動子不斷行進。若逆轉面內與面外彎振模態振動之間超前滯后相位關系，則動子將做反向運動。由上述分析可知，左、右桿上的4個驅動足以及上、下桿上的4個驅動足交替地推動兩自由度方向的運動， 這種多足驅動的方式將提升電機的輸出動力與速度，有利于提高電機的工作效率與穩定性。

4 模態頻率一致性分析

雙H叉合式定子驅動的平面電機作為駐波類電機，其設計的一個重要方面就是須保證各工作模態頻率的一致性以實現模態簡并，而這取決于定子結構尺寸的合理確定。為規劃出定子的優化尺寸，有必要研究定子的特征尺寸與電機工作模態頻率間關系。為此，借助ANSYS的APDL語言，建立了雙H叉合式定子的參數化分析有限元模型，并且利用該模型求得若干主要尺寸對工作模態頻率的影響特性，如圖7所示。由圖可知，當L1增大時則面內、外模態頻率均一致性地下降，這表明可優先通過調節L1來調節電機驅動頻率；當改變L2時，則面外彎振頻率變化較小但面內彎振頻率卻變化較大，即調整該尺寸可較易實現面內、面外模態的一致性。L3對頻率的影響與L1基本相同。當增大L4時則面內彎振頻率增大，面外模態頻率則在一定范圍內基本保證不變，但當增至一定值后，面內模態頻率卻增大。L5對面內模態頻率影響相對較小，但對面外模態頻率影響較大，并且增大L5則面外模態頻率增加。通過對各尺寸進行頻率靈敏度特性分析并結合三相工作模態頻率一致性要求，最終確定出定子結構尺寸如表1所示。

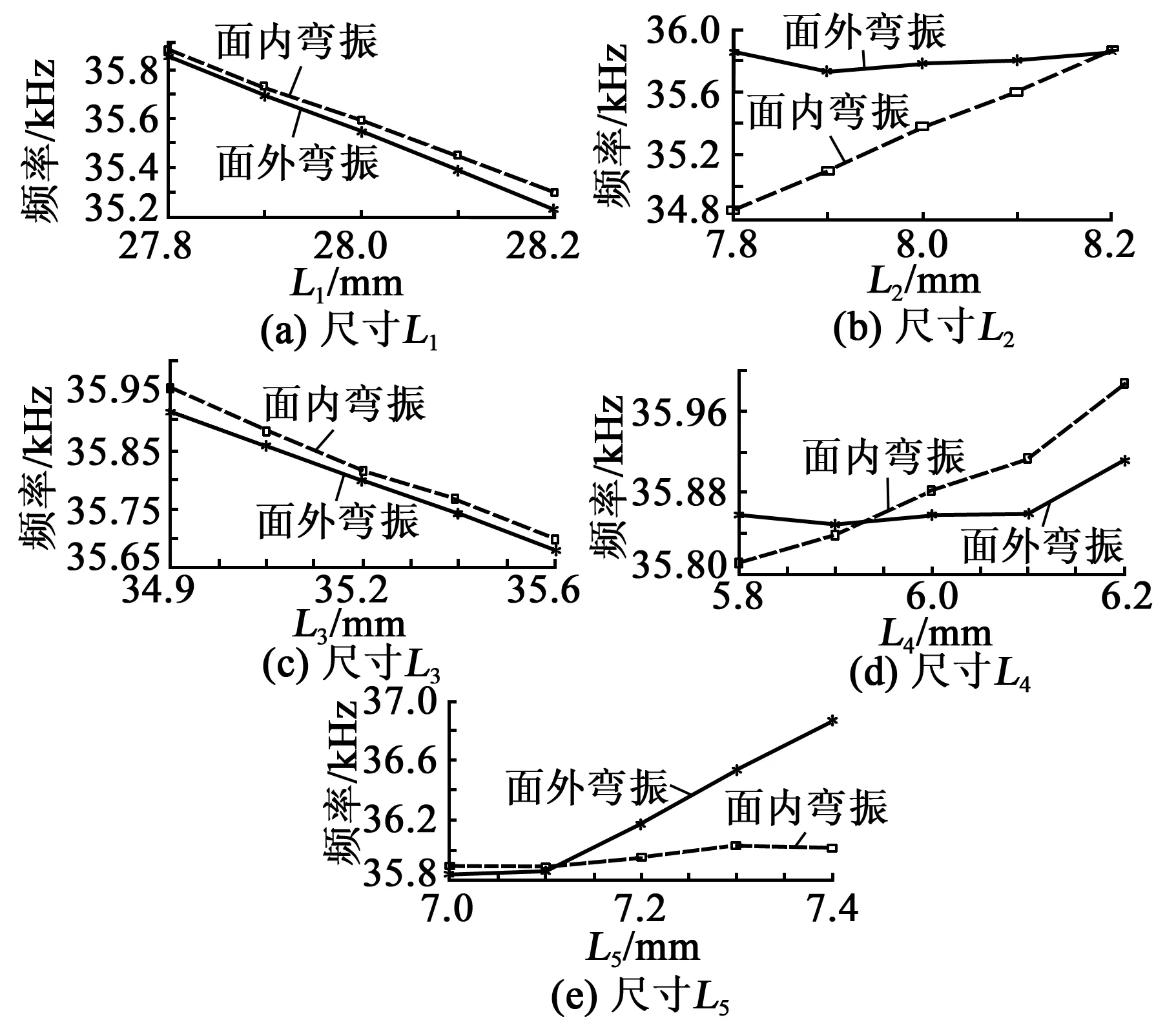
圖7 定子尺寸對工作模態頻率的影響

表1 雙H型定子結構參數尺寸

L1/mmL2/mmL3/mmL4/mmL5/mmL6/mm30.08.736.06.07.41.9

5 定子動力學特性

5.1 定子諧響應特性

平面壓電電機通過激發多相工作模態的諧振實現其運轉，這就要求參與諧振的各相模態振動具有較接近的工作振幅，此外，電機的結構設計還應保證其工作模態附近不應存在高值干擾模態，否則在對電機進行激勵時，易激發出強烈的干擾模態振動，從而使電機無法正常運轉。為便于分析雙H叉合式定子的干擾模態特性，有必要求取定子幅率特性，為此針對表1中的尺寸，利用ANSYS建立定子的機電耦合分析模型，通過在各壓電陶瓷片上施加峰-峰值為250 V的電壓激勵信號并設定32～34 kHz為諧響應求解頻段，再啟動ANSYS的諧響應功能塊，解算出定子的幅頻特性如圖8所示。由圖可知，當對各工作模態采用等幅簡諧電壓進行激勵時，上桿、右桿上的驅動足沿面內和面外振動的振幅不僅處在同一數量級，且幅度相差不大。另外右桿與上桿振幅也較相近。由圖還可知，三相工作模態頻率較接近，并且將32 286 Hz作為電機驅動頻率點時，在32～34 kHz的較寬頻段內并未出現沿x、y向干擾模態。這就表明，當電機的驅動信號頻率與工作模態較接近時，各工作模態均將被有效激勵，驅動足將處于預期的共振或近共振狀態從而推動動子作平面運動。

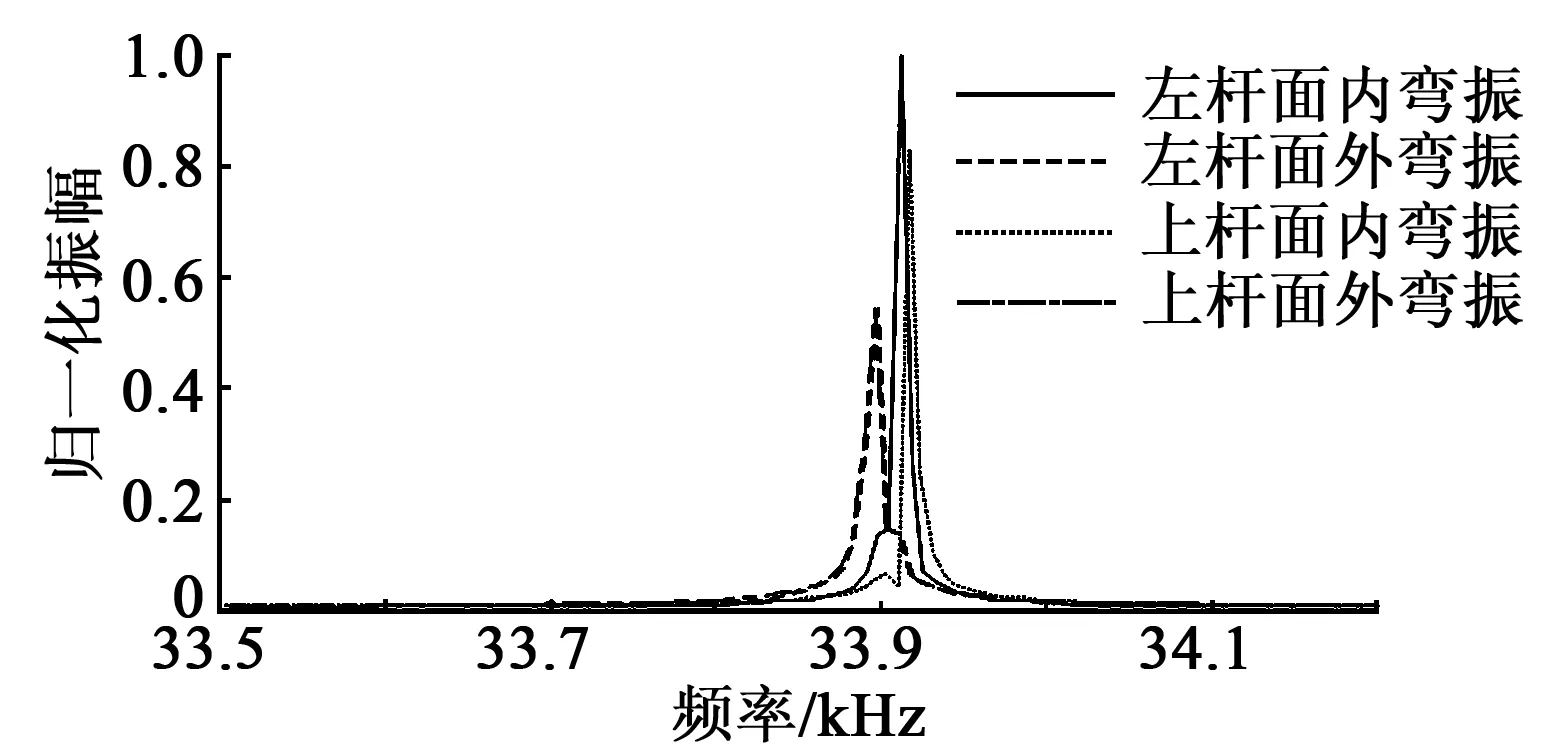
圖8 驅動足的幅頻特性曲線

5.2 驅動足的振動響應

平面壓電電機的運動是建立在驅動足產生橢圓運行軌跡的基礎上，并且為使電機能夠切實有效地運行，要求兩相橢圓軌跡的長、短軸至少應達微米量級，這是因為只有當橢圓幅度足夠大時，定子才能推動動子實現有效步進，并且定子與動子才能實現應有的瞬態接觸與分離。

為驗證驅動足的橢圓軌跡，現按圖2(b)的供電方式對雙H叉合式定子機電耦合分析有限元模型中左、右桿的面內、外工作模態進行諧振激勵，當對各陶瓷片施加32 286 Hz、250 V的驅動電壓后，啟動ANSYS瞬態響應求解器求得驅動足的位移響應如圖9所示。由圖可知，在經過不到1 ms短暫時間后，驅動足振動將逐漸趨于穩定且其沿x、z向的穩態振幅分別達到1.5 μm和1.3 μm，足以達到推動動子的要求。當對所有陶瓷片均通入幅值250 V驅動信號而對定子的三相工作模態同時進行激勵時，還求得驅動足的運動軌跡如圖10所示，由圖可知，左(右)桿和上(下)桿的驅動足分別沿xz和yz面做規范的橢圓軌跡運動，且兩橢圓的長、短軸長度較接近，這進一步驗證電機的工作原理，并且表明雙H叉合式定子驅動的平面電機將具較佳的運動特性。

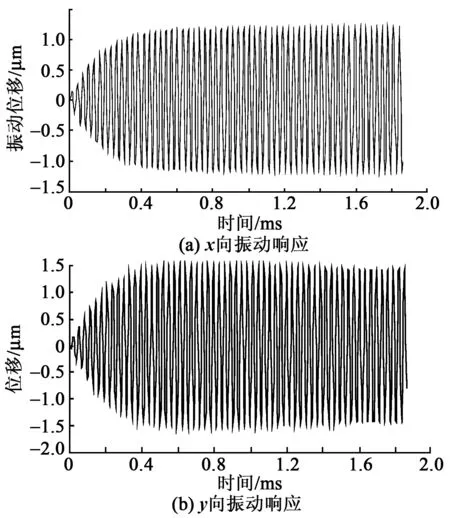
圖9 定子驅動足的振動響應曲線

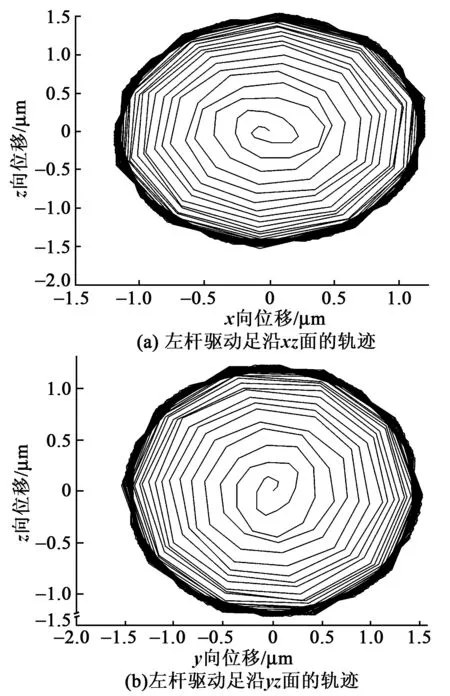
圖10 雙H耦合定子的驅動足運行軌跡

6 驅動足振動調節特性

壓電電機作為一種新型伺服驅動部件，理應具有良好的運動調節特性，這一點落實到定子特性上就是要求驅動足須具有良好的振動調節特性。由于雙H定子采用簡諧電壓進行激勵，故驅動足的運動調節特性需通過改變激勵電壓幅值或需通過改變激勵信號頻率或需通過調節激勵相位差來實現。在保證激勵信號頻率不改變的條件下，本文在定子機電耦合有限元模型上通過施加不同幅值的激勵電壓，求得驅動足的調壓振動特性如圖11(a)所示。由圖11(a)可知，驅動足的振幅與驅動電壓幅值存在一定線性關系，并且增大驅動電壓則驅動足的振幅也增大。同樣，在保證驅動電壓幅值不變的條件下，對定子模型施加不同頻率的激勵信號，得到了驅動足的調頻振動特性如圖11(b)所示，由圖11(b)可知，驅動頻率與振幅間呈現較嚴重的非線性關系，且當驅動頻率小于工作模態頻率時，在一定范圍內增大驅動頻率時則驅動足振幅增大，但當驅動頻率大于模態頻率時，驅動足振幅將隨驅動頻率的增加而下降。此外，在保證驅動電壓和頻率不變的前提下，對定子面內、外模態施以不同相位差的信號同時進行激勵，得到了驅動足的調相振動特性如圖11(c)所示。由圖11(c)可知，當面內、外振動模態激勵信號的相位差等于90°時，驅動足沿純正的橢圓軌跡運行，此時電機性能最穩定，當相位差為45°時，驅動足軌跡為斜橢圓，從而會造成電機運行性能不佳，當相位差為0°時，驅動足軌跡退化為斜直線，使定子和動子始終保持接觸，從而使定子將無法推動動子前行。

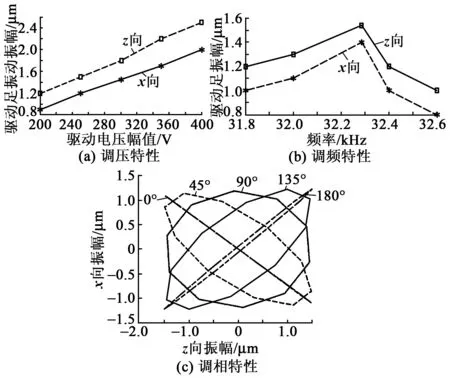
圖11 雙H耦合定子的驅動足振動調節特性

7 電機的裝配結構

裝配設計是構成電機研制的重要方面，裝配方案的好壞直接影響電機性能發揮甚至還關系到電機能否正常運動。電機裝配設計首先須解決定子的夾持與固定問題。為使定子能按預設原理運行，須保證定子的固定不會對其工作模態振型及頻率產生過大影響，為此，在確定定子裝配方案時應盡量選定工作模態的節點為定子夾持和固定點。當然，為限定定子基體的運動自由度，可在定子的單個或多個節點位置對其固定，但因雙H叉合結構的幾何中心點僅為面外工作模態的節點而非面內工作模態的節點，特別是當定子作面內工作模態振動時，定子須沿x或y向產生微量滑移，因此，為保證面內工作模態的純正性，不宜在定子中心處將其固死。為限制定子x、y向移動自由度并補償定子的整體性微量滑移，本文在定子中心處裝配了一個緊固螺釘并在螺釘外套入一個橡膠套管，旨在利用橡膠套的彈性可補償定子的整體微量滑移；為限定定子z向運動并保證不影響定子體沿x或y向的微量滑移，在定子十字板處裝兩個柔性 “U”形壓扣件，并利用其輕壓定子。為減少機座對動子的摩擦，在動子與電機蓋板間裝入滾珠，從而使滾珠間構成滾動副，同時，為防止滾珠掉落，在蓋板下方設置一個托珠板用以托住滾珠，圖12為電機的裝配模型。

8 結論

1) 提出了雙H叉合結構驅動的平面超聲電機原理及其定子壓電超聲換能動力學結構，選定雙H叉合式定子的面外對稱彎振、左(右)桿面內彎振、上(下)桿面內彎振作為電機工作模態。通過面外彎振分別與兩相面內彎振模態的諧振耦合，實現電機的兩自由度平面運動。

2) 建立了雙H叉合式定子的機電耦合分析有限元模型，對定子進行了模態計算和分析，表明定子三相預設工作模態的存在性，通過對電機進行頻率一致性計算，求得定子的基本結構尺寸為30 mm×8.7 mm×7.4 mm。

3) 通過對定子進行瞬態響應分析，模擬出左(右)桿、上(下)桿驅動足的橢圓軌跡，并且結合電機的諧響應特性分析，驗證了電機驅動原理的有效性。

4) 通過對定子進行瞬態響應計算，得到了定子驅動足的調頻、調壓、調相振動特性。

5) 擬定出雙H叉合結構的一種合理的夾持固定方案，并設計出平面電機裝配結構，建立了電機的三維裝配模型。基于所擬夾持固定方案對定子進行固定時，能最大限度地減小定子固定給工作模態帶來的影響。