一種高穩定性壓電驅動電源設計

張玉婷，張文濤，錢 存，張紫楊，陳 云

(桂林電子科技大學 廣西光電信息處理重點實驗室，廣西 桂林541004)

0 引言

隨著現代科技的飛速發展，微定位技術在各領域的地位愈發重要。納米級、亞納米級的定位已成為半導體制造業、航空航天技術、納米醫療器械等領域的核心技術[1-2]。壓電陶瓷促動器作為亞納米級分辨率的位移裝置，具有良好的機械特性與動態特性，廣泛應用于微定位系統中[3-4]。壓電促動器(PZT)的定位精度與驅動電源性能及其特性相關，研究人員普遍使用壓電陶瓷等效靜態電容作為負載電容設計驅動電路[5-6]。實際使用中，壓電陶瓷等效電容隨環境影響及輸入電壓變化有較大波動，影響驅動電源的穩定性。本文設計了一種適應負載電容量變化的壓電陶瓷驅動電源，該研究對微定位系統具有重要的實際意義。

1 驅動電源整體結構

1.1 驅動電源結構框圖

驅動電源主要由微處理器、數模轉換器(DAC)、線性放大電路等組成，整體結構如圖1所示。

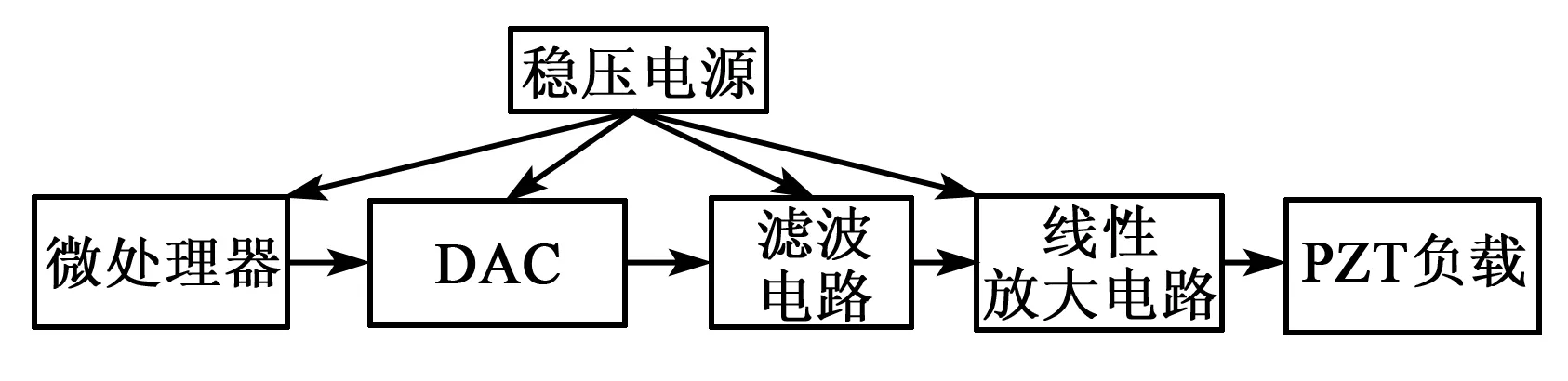
圖1 驅動電源框圖

由圖1可知，微處理器發出數字信號，經濾波、整流后線性放大得到壓電陶瓷位移控制信號。其中，線性放大電路作為驅動電源的重要組成部分，影響控制信號的精度及電源穩定性。

1.2 線性放大電路

壓電陶瓷驅動電源分為電壓控制型與電流型控制型，因電流控制型漏電流問題嚴重，較難控制，故選用電壓控制型。電壓控制型驅動電路的線性放大部分為電路的核心器件，本文采用高壓運放式驅動，其電路圖如圖2所示。

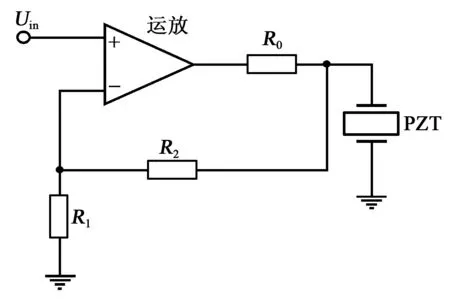
圖2 高壓運放電路

圖2所示的驅動方式具有芯片集成度高，占用空間小，自激現象低等優勢[7]。圖中，R0為運放內阻，R1、R2為反饋電阻，電路的電壓傳輸關系為

(1)

2 動態容性負載分析及補償

2.1 負載容量變化

壓電陶瓷的等效靜態電容是在微電壓、低頻率、無負載、常溫等理想情況下測得的。其值實際大小會隨輸入電壓及溫度的變化而變化[8-9]，變化曲線如圖3所示。

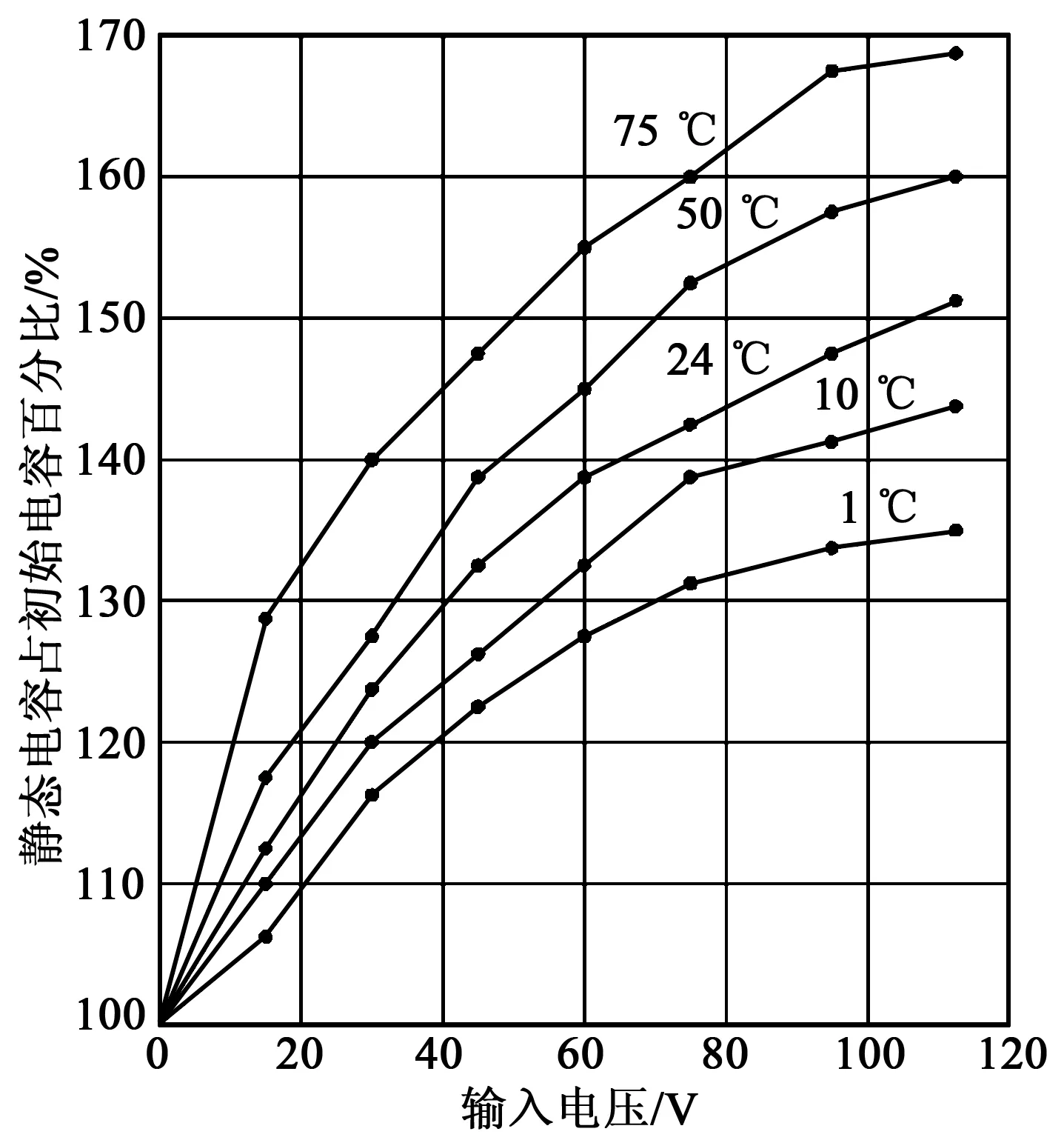
圖3 負載容量變化曲線

由圖3可知，在室溫條件下，驅動電源在輸出電壓為120 V以下時，負載電容量變化可達初始值的1.5倍。因此，設計具有良好動態電容負載適應能力的驅動電源尤為重要。

2.2 容性負載對運放的影響

壓電陶瓷促動器作為運放的容性負載，與運放內阻組成RC振蕩，影響電源系統的穩定[10]。實驗采用PA96運算放大器作為線性運放的核心，分析不同電容量負載對運算放大器開環增益的影響，得到的結果如圖4所示。

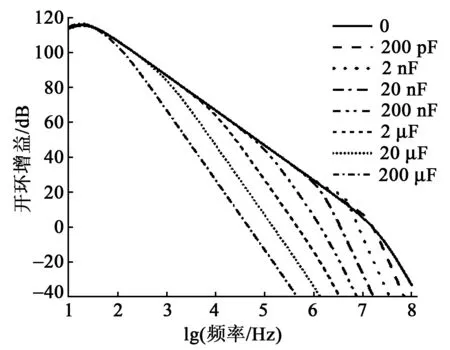
圖4 容性負載對開環增益的影響

由圖4可知，當負載電容量增大時，運放開環增益曲線所加極點頻率變小，減小了運算放大器的帶寬，并使系統提前進入截止頻率，影響運放電路的整體穩定。

PZT作為位移及動能輸出器件，具有納法至微法級以上的等效電容量，由圖4還可知，負載電容量波動對驅動電源穩定性影響較大。本文采用的壓電陶瓷靜態等效電容為1.5 μF，其所加零點頻率為

(2)

式中CL為負載PZT等效電容。此時，系統的開環增益曲線在10.6 kHz點以20倍頻速率下降，并以此速率穿越20 dB增益值，引起系統不穩定，應對其補償。

2.3 動態容性負載補償電路

針對壓電陶瓷等效容量變化的特點，設計了驅動電路結構如圖5所示。圖中，反饋電阻(Rf)、反饋電容(Cf)、PZT組合為單零點補償電路。R、C作為前置濾波，祛除電路中的高頻諧波，Riso為隔離電阻，采用10 Ω小電阻對輸出電壓作平滑處理。

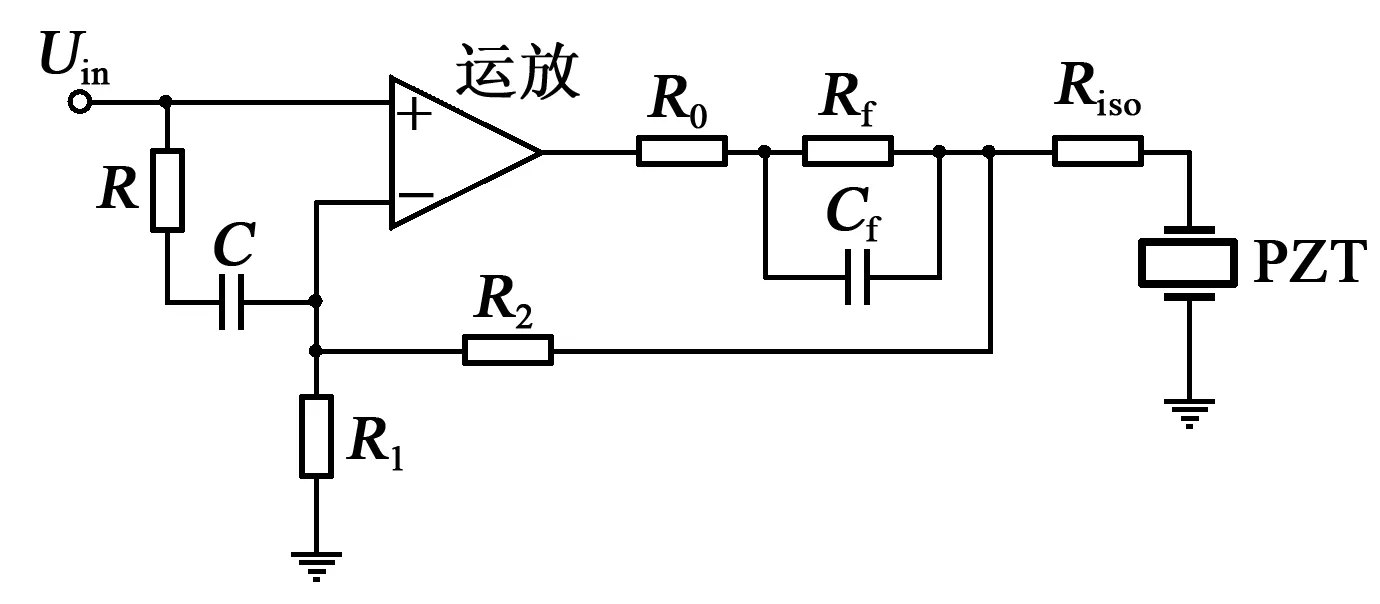
圖5 優化后電路

由圖5可知，該驅動電路具有1個fz與2個極點頻率(包括低頻極點頻率fP1和高頻極點頻率fP2)，則有

(3)

(4)

(5)

將fP1與fz相消，即fz=fP1，可得系統的平衡條件為

RfCf=(R1//R2)CL

(6)

此時，將式(6)代入式(5),系統將產生新極點，新極點頻率fP為

(7)

分析式(6)可知，當CL容量發生變化時，驅動電路的穩定性將受到影響，為使驅動電源仍保持動態穩定，需R1//R2?Rf,Cf?CL。考慮放大倍數與常用反饋電阻的選擇，取R1=10 kΩ、R2=90 kΩ、Rf=100 Ω，CL=1.5 μF，代入式(6)，得Cf=135 μF，fP=10.7 kHz。

已知負載等效靜態容量為1.5 μF，取其1.5倍的電容值2.25 μF，代入式(4)，容量變化引起fP1變化，fP1的值由11.789 Hz變為11.725 Hz，變化量為0.5%，系統平衡條件基本不變，則新極點頻率fP維持在10.7 kHz。

3 線性放大電源電路

3.1 線性放大電路

驅動電源的線性放大電路采用雙極放大結構，整體電路圖如圖6所示。

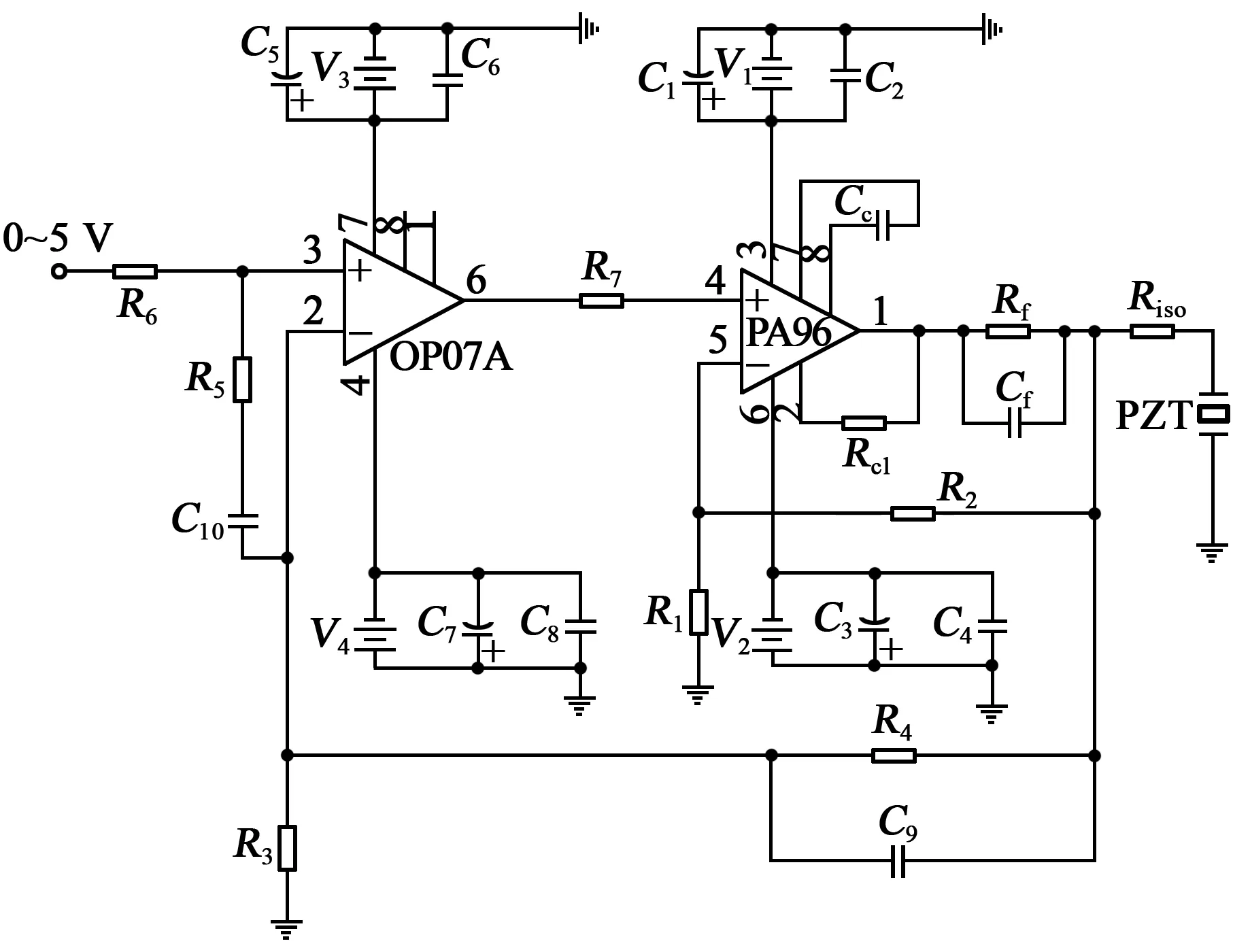
圖6 線性放大電路

由圖6可知，線性放大電路中，前置放電選用OP07A高精度放大器減小系統的失調電壓[7]。R1、R2、R3、R4為反饋電阻，選擇合適的阻值，實現前置放大1倍，運算放大10倍的線性放大。C9為調整電容，可改善環路的穩定性。

3.2 相位補償及限流

運算放大器的相位補償采用純電容補償方式，其值由閉環增益確定。已知運放的放大倍數A=10，則其閉環增益為

Gain=20lgA=20(dB)

(8)

查PA96手冊，選用22 pF電容作相位補償。

高壓運放電路需對輸出電流進行限制，運放輸出電流限制采用限流電阻Rcl，考慮最大輸出電流：

Im=2πUmfmCL=0.94(A)

(9)

式中Um、fm分別為驅動電源的最大電壓、頻率。則Rcl為

(10)

4 電源性能測試

4.1 階躍響應分析

對驅動電源進行階躍響應測試，輸入端采用5 V階躍電壓信號，CL由1.5 μF增至4 μF，每次增加0.5 μF，得到驅動電源的輸出電壓階躍響應曲線如圖7所示。

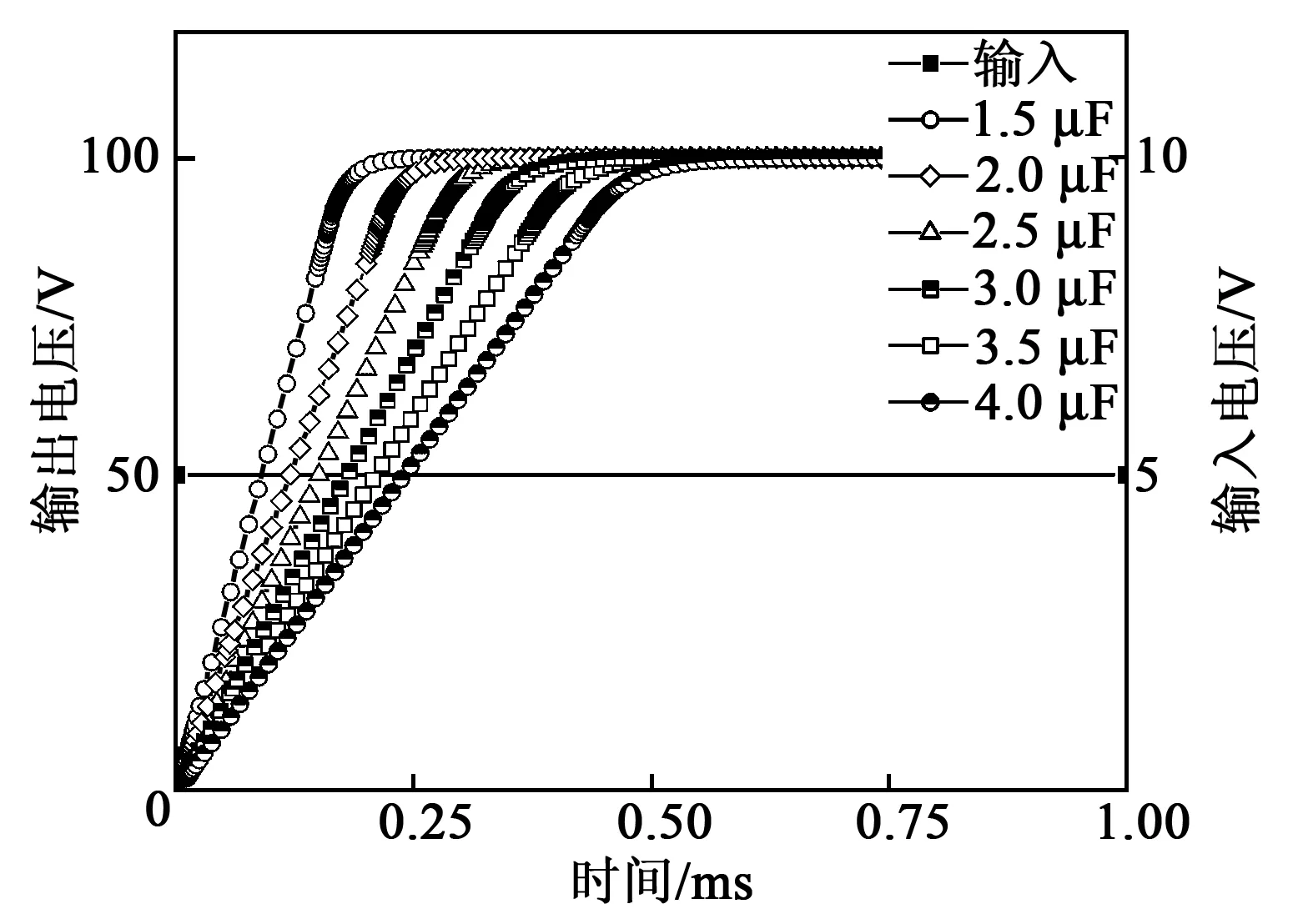
圖7 驅動電源的輸出電壓階躍響應曲線

由圖7可知，當CL=1.5 μF時，系統的驅動電源輸出電壓階躍信號在0.2 ms內平滑上升至100 V，且無超調量。當CL逐漸加大時，系統的階躍響應時間變長，信號質量良好。考慮驅動電源使用頻率為1 kHz，當階躍時間為半個周期即0.5 ms時，負載容量為臨界值4 μF，即驅動電源在CL為0～4 μF時，均具有良好的階躍響應。

4.2 動態跟隨分析

在1 kHz使用頻率時，系統的動態穩定性也尤為重要，可分析驅動電源動態跟隨效果。輸入信號采用幅值2.5 V，正向偏置電壓2.5 V的1 kHz正弦信號，得輸出電壓信號如圖8所示。

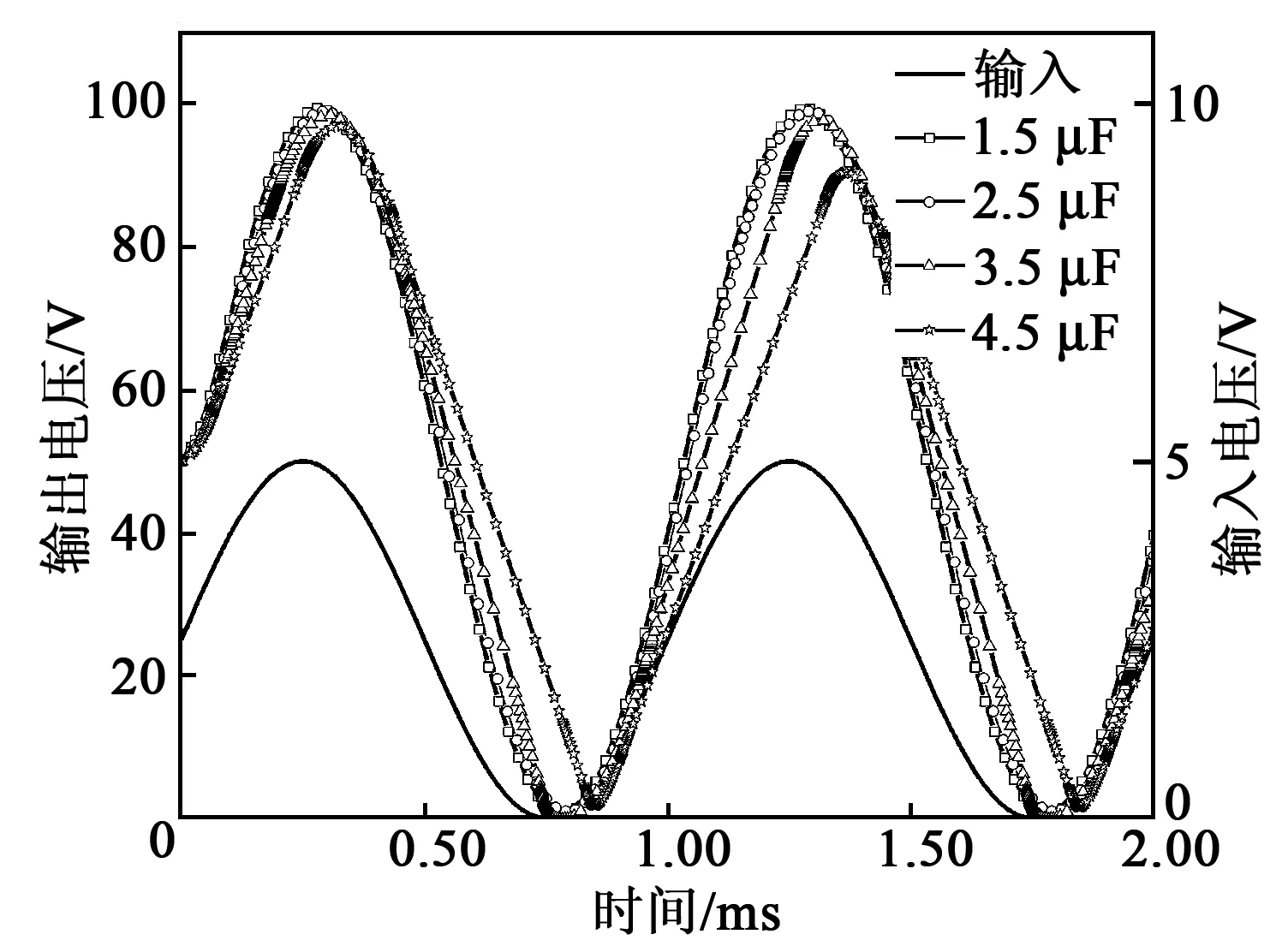
圖8 動態跟隨曲線

由圖8可知，在CL為1.5～3.5 μF變化時，系統輸出電壓信號跟隨效果良好，電壓曲線為正弦信號。而當CL=4.5 μF時，系統的輸出電壓曲線第二峰值缺壓，無法達到額定輸出值。所以，驅動電源在CL為0～3.5 μF時，具有良好的動態響應。

4.3 誤差分析

對驅動電源進行線性誤差分析，經多次測量得系統的線性誤差與CL大小無關，誤差測量結果如圖9所示。

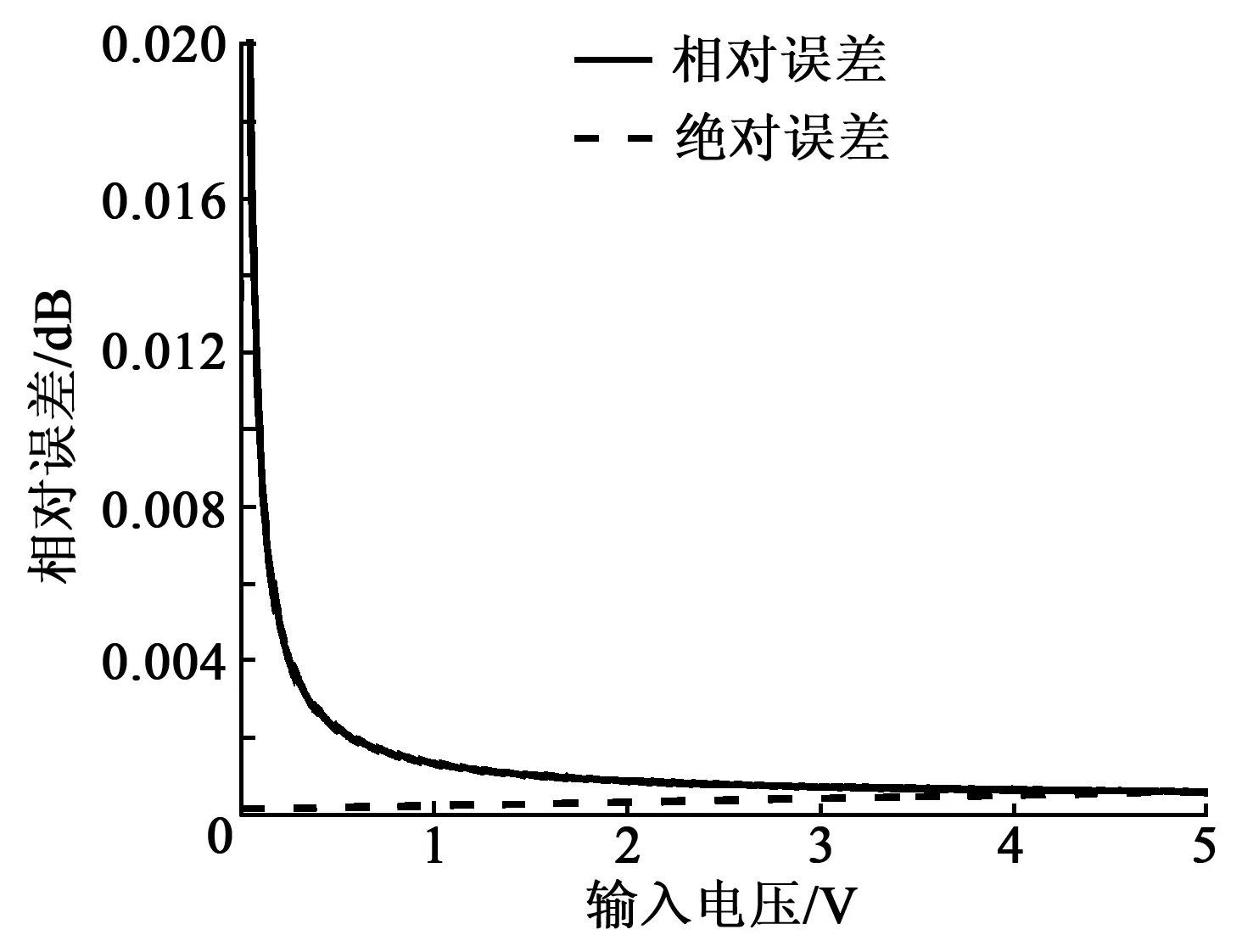
圖9 線性誤差

由圖9可知，驅動電源在0～100 V時，其輸出相對誤差在0.02%以下，且線性誤差在0.7 mV以下，具有較高的線性度與可信度。

5 結束語

本文首次提出了一種適用于變電容負載的驅動電路，動態容性負載對電源穩定性進行分析。通過驗證電路性能，表明該驅動電路的電容量適用于0～3.5 μF，大于設計需求范圍(0～2.25 μF)，為壓電陶瓷驅動提供了新思路。