基于跟蹤微分器的姿控噴管故障檢測

張 凱，楊小龍，楊宇和

(北京宇航系統工程研究所，北京 100076)

0 引 言

航天飛行器包括衛星、運載火箭、彈道導彈等，具有重要的經濟價值或戰略價值，其設計要求具有極高的可靠性，具有容錯控制能力的姿控系統是高可靠性的重要保障，因此對于航天飛行器姿控系統的故障診斷便成為必要[1-2]。故障診斷方法包括基于模型的故障診斷、基于信號的故障診斷和基于知識的故障診斷[3-4]。

現有的關于航天飛行器姿控噴管故障診斷國內外文獻較少，國內相關文獻多集中于伺服機構的故障檢測、診斷[5-7]。張亞婷等[8]提出了姿控噴管的故障診斷方法，即通過設計觀測器，對比觀測器輸出信號和真實信號的殘差，從而判定故障是否發生，屬于基于模型的故障診斷。該方法的關鍵是故障發生時殘差信號閾值確定[9]，通過大量仿真歸納給出閾值的確定方法，尚不具備普適性。

根據文獻[10]，觀測器方案對于初始的故障不敏感，故障檢測有較長延時。本文采用跟蹤微分器來估計姿控噴管實際輸出力矩，通過與指令力矩的對比來檢測故障。微分器應用于故障檢測領域的文獻較少，文獻[11-12]研究了基于微分器的傳感器故障檢測，文獻[13]設計了自適應增益的微分器，并應用于飛機舵面震蕩的故障診斷。本文從理論上推導了估計力矩的變化范圍，設計了根據指令和角速度等變量自適應變化的估計力矩變化包絡，解決了閾值選取問題，并且通過仿真驗證了所提方法的有效性。

1 研究模型及姿控噴管布局

研究對象為一假設的航天飛行器模型(模型參數為非真實參數，但不影響其對本文所提出方法驗證的可參考性)，研究目的在于識別其空間飛行段的姿控噴管故障。其姿控噴管布局尾部視圖如圖1所示。該模型為剛體，不考慮柔性。P1～P6為姿控噴管，單個噴管推力為100N，P1，P6，P3，P4控制俯仰；P1，P4，P3和P6控制滾轉；P2，P5控制偏航。相關姿控動力系統性能參數如表1所示。

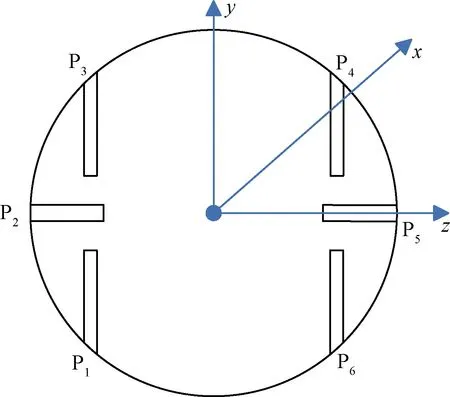
圖1 模型噴管布局

噴管推力用為一階環節加延時環節模擬，表示如式(1)，其中延時環節的延時時間和一階環節的時間常數滿足熱啟動加速性和熱關閉減速性的要求。

(1)

2 跟蹤微分器設計

由于實際的執行機構存在安裝偏差、推力大小偏差、延時等不確定因素，姿控噴管的輸出與指令期望的輸出會有一定的誤差。姿控噴管正常工作時，誤差會在一定“限度”內，當姿控噴管出現故障時，姿控噴管輸出與指令期望輸出會有較大不一致，誤差超過這個“限度”。因此如果能估計出姿控噴管的輸出并與指令期望的輸出做比較，并尋找到合適的“限度”，便可以通過判斷誤差是否在“限度”之內來確定姿控噴管是否出現故障。

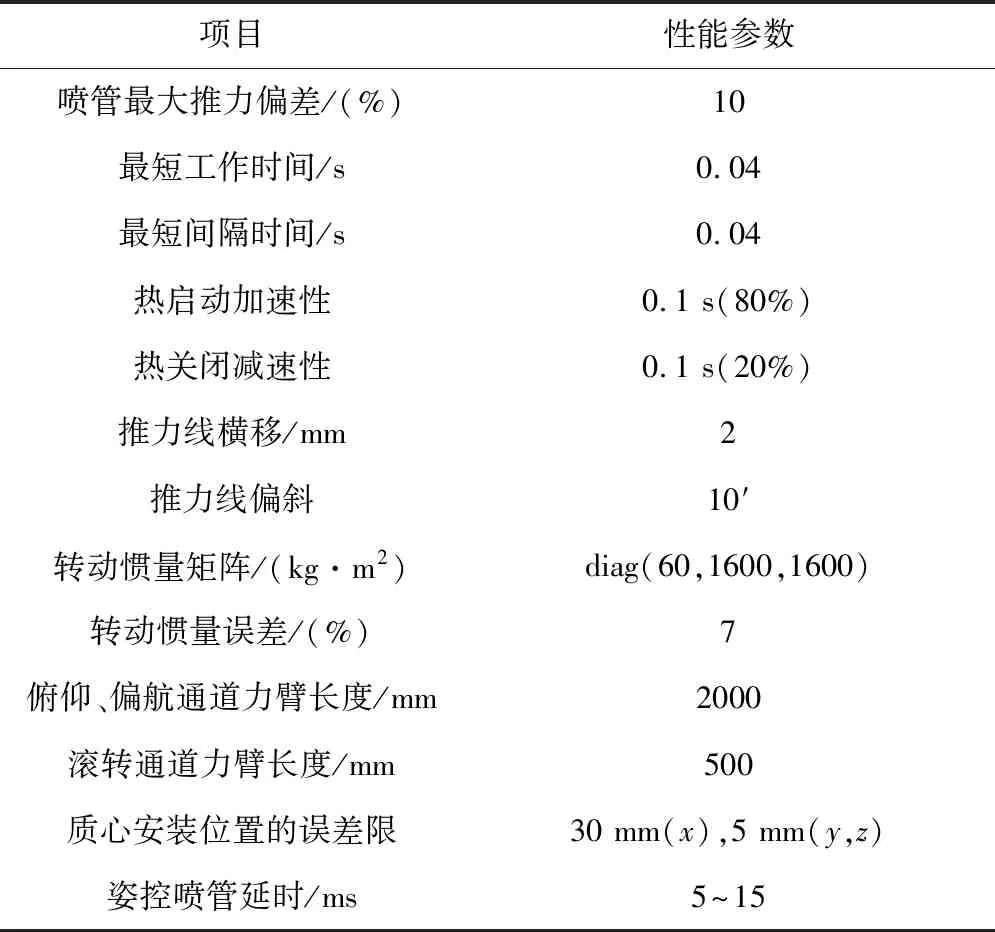
表1 姿控動力性能參數

對于本文中所討論的航天飛行器的姿態運動，其角速度可測，可以利用跟蹤微分器跟蹤角速度來得到角加速度，進而得到噴管實際的輸出，因此構造跟蹤微分器是本方法的基礎。

考慮航天飛行器的姿態運動，可視其為剛體，其動力學方程如下

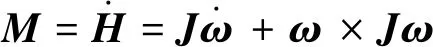
(2)

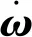
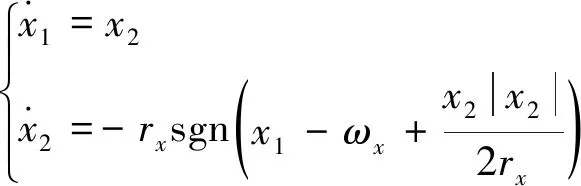
(3)

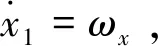
實際使用的跟蹤微分器為其離散形式，離散系統中從非零初值到達原點的最速控制綜合函數記為

u=fhan(x1,x2,r,h)

(4)

展開如下[14]，h為離散步長

(5)

其中，

fsg(x,d)=(sgn(x+d)-sgn(x-d))/2

(6)

以x軸為例，用x1-ωx替代x1，則得到離散化的跟蹤微分器

(7)

如果輸入信號被噪聲污染，那么跟蹤微分器輸出的微分信號將會放大噪聲，但是如果將fh=fhan(x1,x2,r,h)中的h改為與步長獨立的新變量h0，將其取為適當大于步長的參數，就可以抑制微分器對噪聲的放大。

與原微分信號相比，理想的跟蹤微分器輸出的微分信號應該延時小且噪聲小，為減小延時，應該增大r且減小h0，但這會放大噪聲；為減小噪聲則需要執行相反的操作從而使延時增大。綜合考慮延時和噪聲的影響選取合適的r值和h0值也是不可行的，因為跟蹤微分器跟蹤較大的微分信號時會有比較大的延時，跟蹤小的微分信號時會有比較小的延時，在抑制噪聲的前提下難以選取合適的r和h0來減小跟蹤大微分信號的延時，并且這種不一致的延時難以補償。

為保證噪聲較小且延時可補償，本文采用串聯低通濾波器。首先選取合適的h0和比較大的r值，此時跟蹤微分器輸出的信號噪聲很大,但對于大的微分信號和小的微分信號的延時都很小,所以可以忽略兩種延時的不一致；然后將這一信號通過低通濾波器，獲得濾除噪聲后的微分信號,低通濾波器會使信號產生一個一致的延時,跟蹤微分器的延時遠小于濾波器的延時，因此可以忽略微分器的延時，只補償低通濾波器的延時就可以達到延時補償的目的，延時的具體補償方法見第3.3節。

低通濾波器的設計可以采用一階環節或二階環節等。由文獻[13]可知，小時間常數的一階環節可近似為延時環節，有

(8)

由模型參數可知，姿控噴管最短工作時間為0.04 s，因此角加速度增大、減小的最短周期為0.08 s，因此如果帶寬達到1/0.08·2π≈78.5便可以達到要求，實際的帶寬選擇可參考此值并根據噪聲的特性來考慮，如果低通濾波器為二階環節，可將其等效為兩個串聯的一階環節，并根據式(8)計算低通濾波器造成的延時。

3 控制力矩包絡分析

根據得到的微分信號可以解出飛行器所受的力矩，該辨識力矩與指令力矩的誤差由兩部分構成：實際力矩與指令力矩的偏差，辨識力矩與實際力矩的偏差。前者的主要構成是姿控噴管推力偏差、姿控噴管安裝誤差、質心誤差，后者的主要構成是轉動慣量偏差、跟蹤微分器輸出信號的偏差。指令力矩加上這兩種誤差和的上限便是上包絡，指令力矩加上這兩種誤差和的下限便是下包絡，若辨識力矩處于上下包絡內便可認為其工作正常，反之則發生了故障。

3.1 實際力矩與指令力矩的偏差

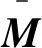
(9)

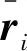
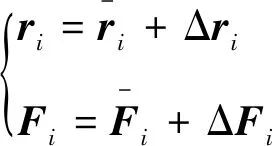
(10)

式(9)化簡到最后右邊有3項，第3項屬于高階小量，可以直接略去；對于第1項中的ΔFi，包括了推力線的偏斜導致的方向變化和推力不穩定導致的推力大小變化，然而推力線偏斜僅僅有10′，tan(10′)<0.003，可以忽略，因此只考慮推力大小變化；對于第2項，推力線偏移只有2 mm，但是考慮ri為飛行器質心到噴管中心線上的垂點的矢徑，因此質心的變化也會影響Δri，故將Δri拆解為2部分如下

(11)

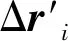
(12)

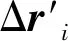
由于每時每刻的噴管的開關狀態都不一樣，所以式(12)要添加噴管指令的開關信息

(13)

其中，sw(i)為第i個噴管的開關函數，其值取1或者0，1表示噴管開，0表示噴管關。令Δrxm，Δrym，Δrzm分別為Δrc在3個方向上的誤差限，皆為正數，即有

(14)

將式(13)等號右邊第二項展開，考慮到Δrc的分量都為正，得到

(15)

式中：sw(i)可以通過控制器指令得到，除此之外其他所有量都已知。將式(13)等號右邊第一項展開可得

(16)

式中：sw(i)可以通過控制器指令得到，除此之外其他所有量都已知。因此實際力矩與指令力矩的偏差的上限可以由式(15)和式(16)確定。

3.2 辨識力矩與實際力矩的偏差

根據跟蹤微分器得到的角加速度和已知的標稱轉動慣量，可以計算飛行器所受力矩，辨識的力矩表示為

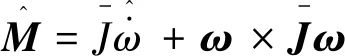
(17)

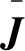
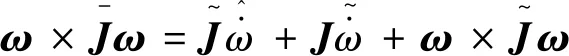
(18)

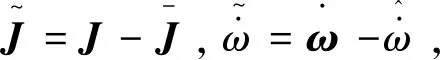
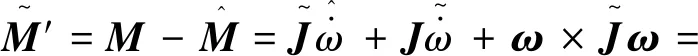
(19)

可整理得到誤差力矩的上限如式(20)

(20)

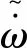
(21)

由此可知辨識力矩與實際力矩的偏差主要由轉動慣量偏差和跟蹤微分器輸出信號的誤差兩部分構成，其中轉動慣量造成的偏差又由兩部分構成：角加速度引起的辨識誤差和角速度耦合引起的辨識誤差。

3.3 包絡線的確定

(22)

下限為

(23)

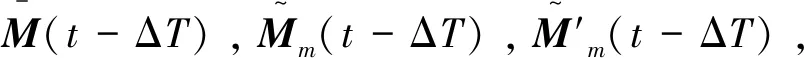
其中實際力矩與指令力矩的偏差由推力大小偏差和質心位置偏差構成，二者表達式見式(15)和(16)，其表達式包含sw(i)即姿控噴管的開關函數，意味著這兩項偏差只在姿控噴管開啟時起作用，而姿控噴管的性能有一個上下限，即從下達姿控噴管指令開始到姿控噴管輸出到達均勻，其整個過程的“時間-推力”曲線可以由兩條姿控噴管性能包絡曲線來框定，上下包絡表示姿控噴管正常工作時輸出推力的最大值和最小值。

對單個噴管而言，當噴管開啟時，其上包絡線為噴管最大推力值經過一階環節和延時環節得到的曲線，其中延時環節的延時和一階環節的時間常數都要小于噴管的最好性能對應的數值；當噴管關閉時其上包絡線為0經過一階環節和延時環節得到的曲線，其中延時環節的延時和一階環節的時間常數都要大于噴管的最差性能對應的數值，其特點總結為：推力大，升的快，降的慢。

當噴管開啟時，其下包絡線為噴管最小推力值經過一階環節和延時環節得到的曲線，其中延時環節的延時和一階環節的時間常數都要大于噴管的最差性能對應的數值；當噴管關閉時其下包絡線為0經過一階環節和延時環節得到的曲線，其中延時環節的延時和一階環節的時間常數都要小于噴管的最好性能對應的數值，其特點總結為：推力小，升的慢，降的快。

因此確定力矩包絡時，對于所有由噴管引起的力矩偏差都要通過上下包絡線的延時和一階環節再疊加到指令力矩，而不是簡單加減。

因為在推導過程中略去了一些小量，因此在真實的包絡線確定過程中可以在各個通道疊加一個常值力矩作為補償。

當包絡確定后如果辨識的力矩曲線越過了包絡線并持續了一段時間tconti便可認為噴管發生了故障。tconti的取值要綜合考慮誤檢率和漏檢率,由于存在噪聲,噴管無故障時辨識力矩可能短時間超過力矩包絡,故tconti太小會造成誤檢;故障與指令沖突時該故障才能暴露,若某故障暴露時間短則辨識力矩超過包絡的時間就短,因此tconti太大會造成漏檢。

4 仿真校驗

通過仿真驗證所提方法的有效性，包括跟蹤微分器的有效性，姿控噴管正常工作情況下的誤檢概率以及姿控噴管故障時是否能迅速檢測出故障。

仿真中跟蹤微分器參數為h0=0.005 s，rx=3333，ry=250，rz=500；低通濾波器為

(24)

(25)

噴管啟動(關閉)時下(下)包絡的傳遞函數環節

(26)

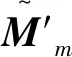
4.1 跟蹤微分器

仿真初始姿態為[0°,0°,0°]，目標姿態為[50°,50°,50°]，控制器為采用極限環方法，各通道獨立控制。以x軸為例，仿真如圖2所示。

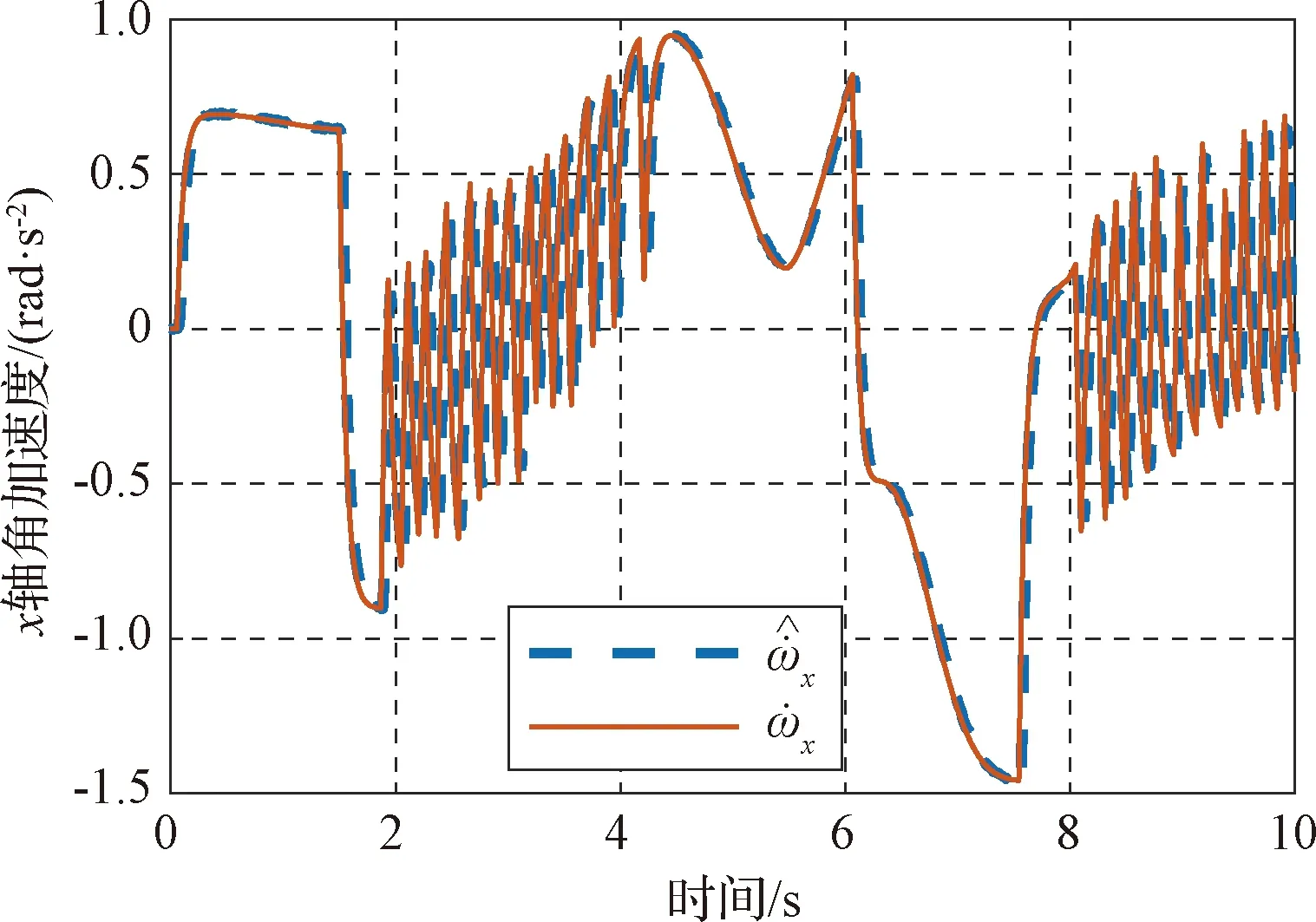
圖2 跟蹤微分器仿真效果

圖2表示跟蹤微分器跟蹤軸x的角加速度曲線，可見跟蹤微分器的性能良好。

4.2 無故障情形

由前文的力矩偏差分析可知，辨識力矩與指令力矩誤差的主要原因為噴管推力大小誤差、質心偏移、轉動慣量誤差、角速度耦合、角加速度辨識誤差，其中前三個原因需要通過硬件改良，角加速度辨識誤差的減小需要良好的跟蹤微分器，角速度耦合可以在姿態機動過程中極大程度避免，比如姿態機動時各個軸依次機動而非同時機動，因此在這一部分中進行了兩組仿真，第一組耦合比較嚴重，模擬極限情況，第二組為耦合不嚴重，模擬正常情況。

兩組仿真中各個有誤差的參數均取其極限值，比如推力標稱值100 N，偏差為10%，則仿真中姿控噴管推力為110 N或90 N。這些取極限的參數包括推力大小、推力線橫移、推力線偏斜、轉動慣量、實際質心與理論質心距離的誤差。

對第一組仿真，仿真初始姿態為[0°,0°,0°]，目標姿態為[50°,50°,50°]，控制器為采用極限環方法，各通道獨立控制，在三軸均大角度機動時姿態會發散，各通道角速度耦合嚴重，驗證在此極端情況下的包絡選取的合理性。該組仿真共進行了2552次，每次仿真10 s。其中有81次辨識的力矩曲線越過了包絡線，但其中越過包絡線時間最長的一次也僅僅持續了0.004 s，此值遠小于tconti=0.02 s，因此可認為此情況下誤檢率為0。圖3給出該組仿真中某次仿真的曲線。

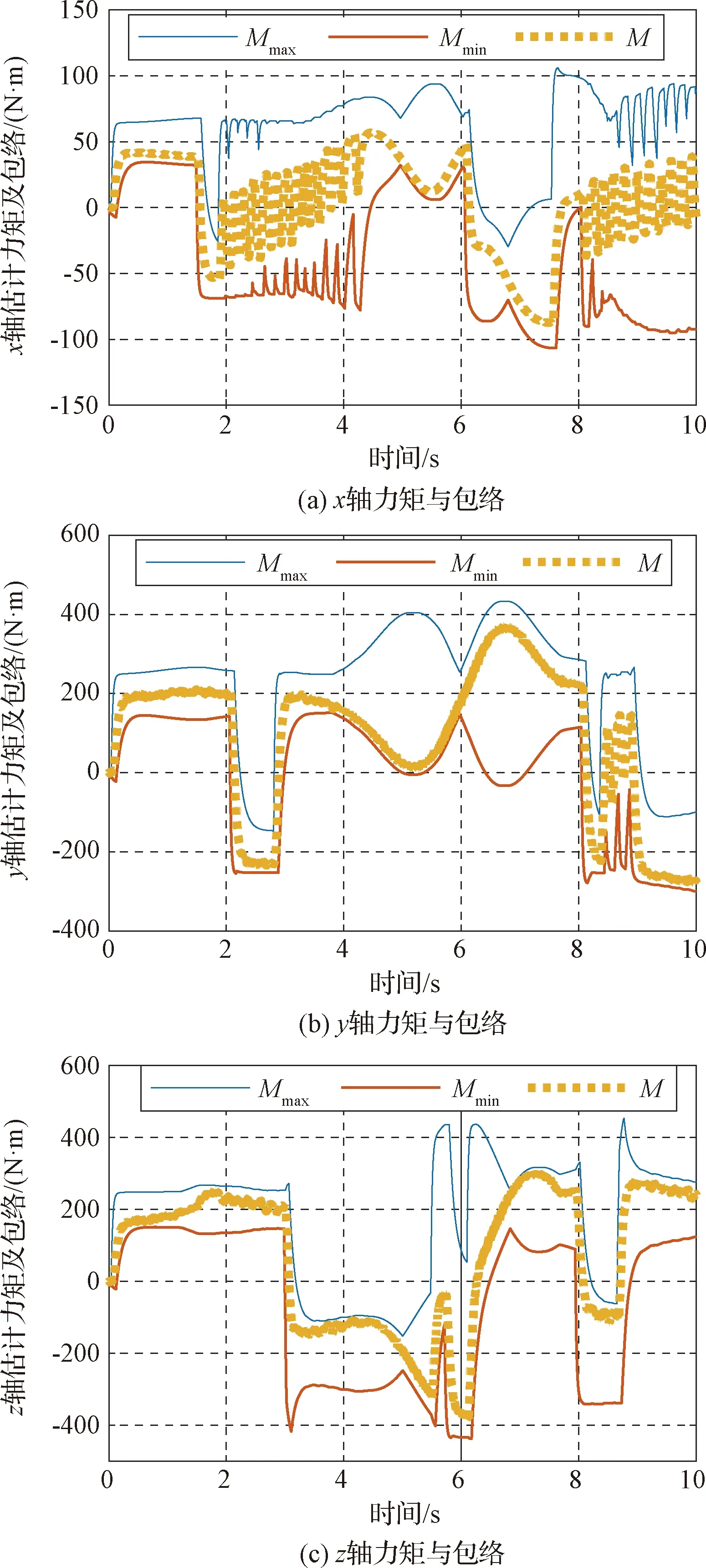
圖3 無故障檢測(嚴重耦合)

對第二組仿真，初始姿態[0°,0°,0°]，目標姿態[10°,10°,10°]，其余條件與第一組相同。該組仿真共進行了884次，每次仿真10s。其中有0次辨識的力矩曲線越過了包絡線，因此可認為此情況下誤檢率為0。圖4給出該組仿真中某次仿真的曲線。

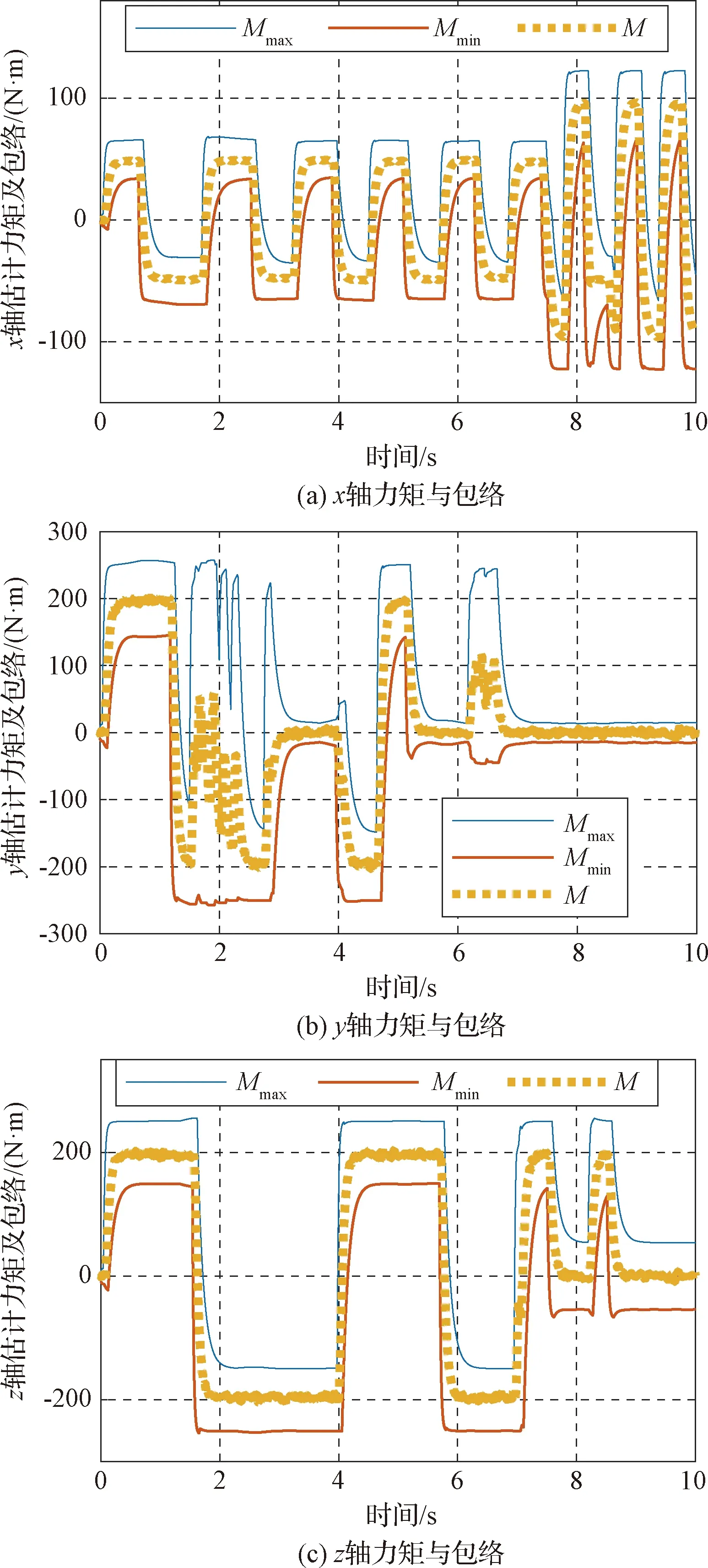
圖4 無故障檢測(一般耦合)

4.3 有故障情形

姿控噴管故障包括噴管常開、噴管常關與噴管極性接錯3種。本組仿真初始姿態為[0°,0°,0°]，目標姿態為[10°,10°,10°]，控制器與無故障情形相同。每次仿真時長10 s，第5 s時加入故障，假設3種故障發生概率相同。需注意當故障與指令發生沖突時故障才能凸顯，例如發生P1噴管常開的故障，若指令一直讓P1輸出推力，則無法檢測P1的故障；同理若發生噴管常關故障，只有當指令讓該噴管輸出推力時故障才凸顯；若發生極性接錯故障則當兩個噴管中的一個接收到打開指令、一個接收到關閉指令時故障才凸顯。

因此仿真中以5 s后指令第一次與噴管故障沖突作為故障發生的時刻，以辨識力矩曲線超過包絡并持續tconti=0.02 s作為故障檢出時刻，故障檢出時刻減去故障發生時刻為故障檢測所用時間。

本組仿真共進行675次，有24次未能檢測出故障。其中12次因為故障與指令未發生沖突，故障未能凸顯；另外12次因為與故障沖突的指令從5 s持續到5.015 s，持續時間僅15 ms，故障未充分暴露，因此未檢測出。檢出故障的651次仿真中大部分情況下可在0.1 s內檢出故障，檢測用時最短0.0595 s，最長3.1595 s，這是因為第一次指令與故障沖突時持續時間較短，故障未能充分暴露，因此在后面的指令、故障沖突中才檢出故障，故而計時較長。

圖5給出某次故障檢出的仿真。

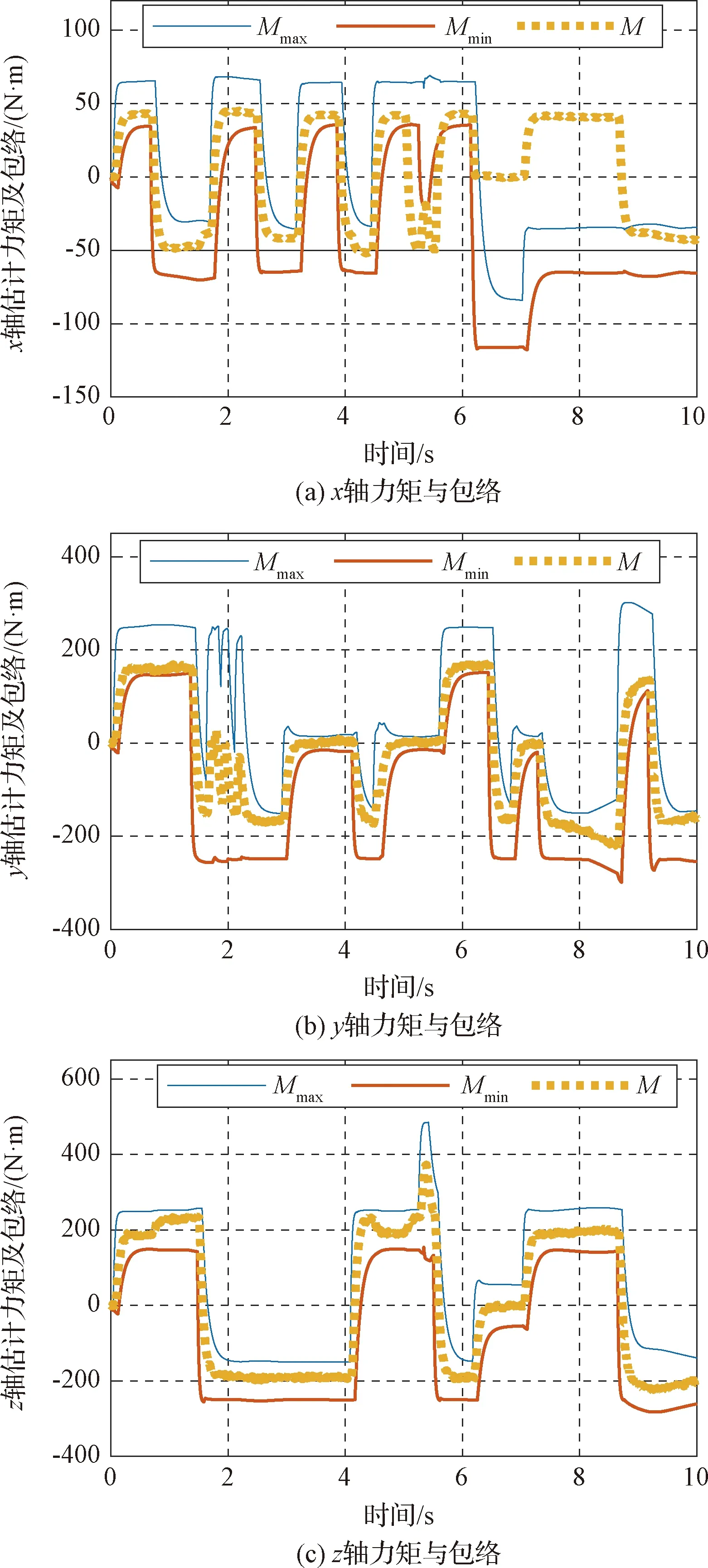
圖5 有故障檢測

其中此次故障為P3，P4噴管極性接錯，指令與故障發生沖突時刻為5.0005 s，故障檢出時刻為5.0615 s，檢測用時為0.061 s。

5 結 論

本文提出了一種航天飛行器姿控噴管的故障檢測方法，只需要得到角速度測量信號與姿控噴管指令信號便可以根據本文提供的方法進行姿控噴管的故障檢測，這兩種信號容易測量得到。本文中提到的包絡設計方法需要得到噴管推力偏差、轉動慣量偏差、噴管安裝誤差等參數，這些也可以得到。仿真表明：該方法誤檢率幾乎為零且故障檢出率高，可靠性強，并且檢測時間短，具有一定的實用價值。