Neuman平均關于算術和調和平均的精確不等式

王君麗，徐會作，李少云

（1.臺州科技職業學院成人教育學院，浙江臺州318020；2.溫州廣播電視大學教師教學發展中心，浙江溫州325013；3.溫州廣播電視大學終身教育指導中心，浙江溫州325013）

對 于p ∈? 和a,b ＞0 且a ≠b，則p 階 冪 平 均[1]=。對于固定a,b ＞0和a ≠b關于p ∈? 是連續且嚴格單調上升的。調和平均、幾何平均、算術平均和二次平均是冪平均的特殊情形：

分別是第一類Seiffert平均、Neuman-Sándor平均、第二類Seiffert平均、對數平均、第一類Yang平均和第二類Yang 平均[4]，并且有不等式L( a,b )＜V( a,b )＜P( a,b )＜U( a,b )＜NS( a,b )＜T( a,b )對所有a,b ＞0且a ≠b成立。

近年來，Schwab-Borchardt平均及其派生平均與不同階冪平均的凸組合或各種特殊組合的序關系研究，得到國內外數學研究者的關注，有關Schwab-Borchardt平均的新派生平均被提出，一些重要平均值不等式被發現，Neuman平均就是其中一種。

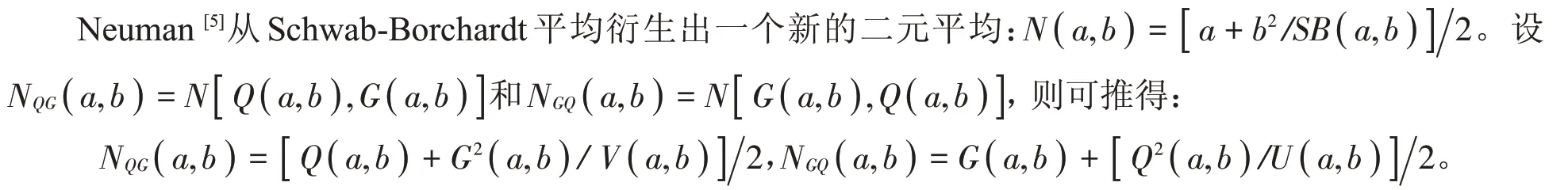
沈林昌等[6]證明了雙向不等式

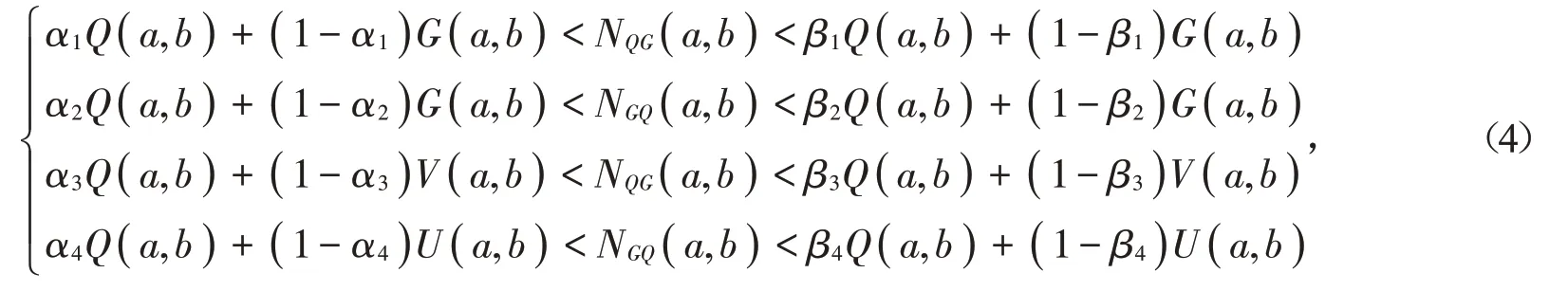
對所有a,b ＞0 且a ≠b 成立當且僅當α1≤1∕3，β1≥1∕2，α2≤2∕3，β2≥π∕4，α3≤0，β3≥1∕2，α4≤0 和β4≥( π2-8 )∕[ 4( π-2 )]=0.409 4…。

根據不等式（4），可推得

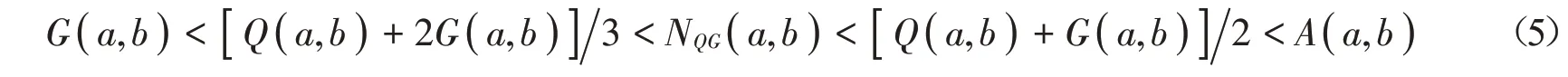
對所有a,b ＞0且a ≠b成立。

何 曉 紅 等[7]證 明 了α ≤2log2=1.178 5… 和β ≥4∕3 是 雙 向 不 等 式Mα(a,b)＜NGQ(a,b)＜Mβ(a,b)對所有a,b ＞0且a ≠b成立的最佳參數。受不等式(5)的啟發，本文主要討論是否存在最佳參數α1,α2,β1,β2∈( 0,1 )使得雙向不等式

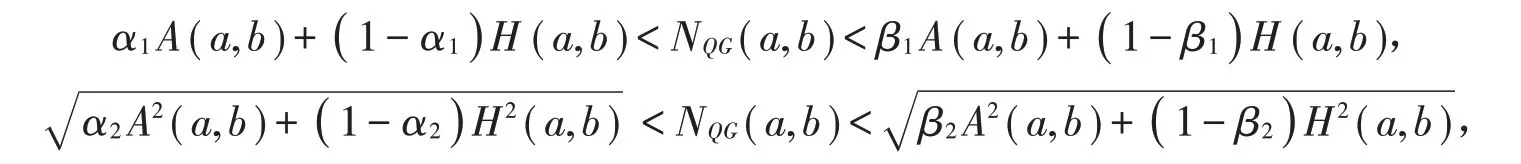
對所有a,b ＞0且a ≠b成立。

為了討論上述問題，需要先介紹下面兩個引理。

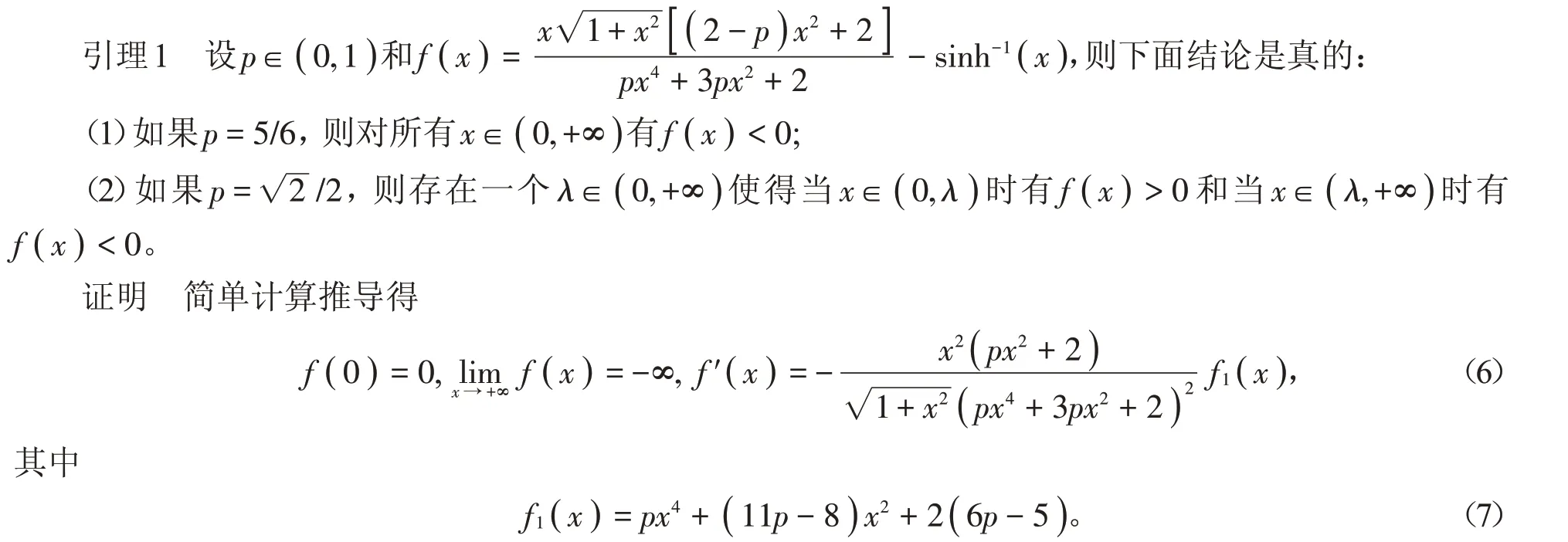
下面分兩種情形討論：

（1）當p=5∕6時，（7）式變為

對所有x ∈( 0,+∞ )成立，所以，由（6）、（8）式得到對所有x ∈( 0,+∞ )有f( x )＜0。

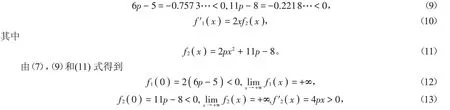
對所有x ∈(0,+∞)。

由（13）式可知存在λ0∈( 0,+∞ )使得當x ∈( 0,λ0)時f2( x )＜0，當x ∈( λ0,+∞ )時f2( x )＞0。由（10）、（12）式可知，當x ∈( 0,λ0)時f1( x )＜0；當x ∈( λ0,+∞ )時，f1( x )在區間( λ0,+∞ )內嚴格單調上升且f1( λ0)＜0，易知存在λ1＞λ0使得當x ∈( λ0,λ1)時f1( x )＜0，當x ∈( λ1,+∞ )時f1( x )＞0。綜上可知，存在當x ∈( 0,λ1)時f1( x )＜0；當x ∈( λ1,+∞ )時f1( x )＞0。

同上分析，由（6）式并結合x ∈( 0,λ1)時f1( x )＜0，x ∈( λ1,+∞ )時f1( x )＞0，易知存在λ ＞λ1使得當x ∈( 0,λ )時f( x )＞0；當x ∈( λ,+∞ )時f( x )＜0。

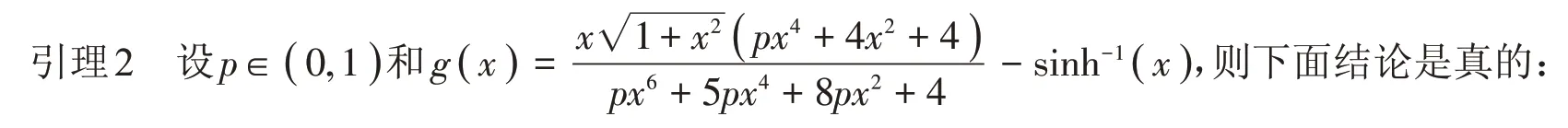
（1）如果p=5∕6，則對所有x ∈( 0,+∞ )有g( x )＜0；

（2）如果p=1∕2，則存在一個μ ∈( 0,+∞ )使得當x ∈( 0,μ )時有g( x )＞0 和當x ∈( μ,+∞ )時有g( x )＜0。

證明 簡單計算可得

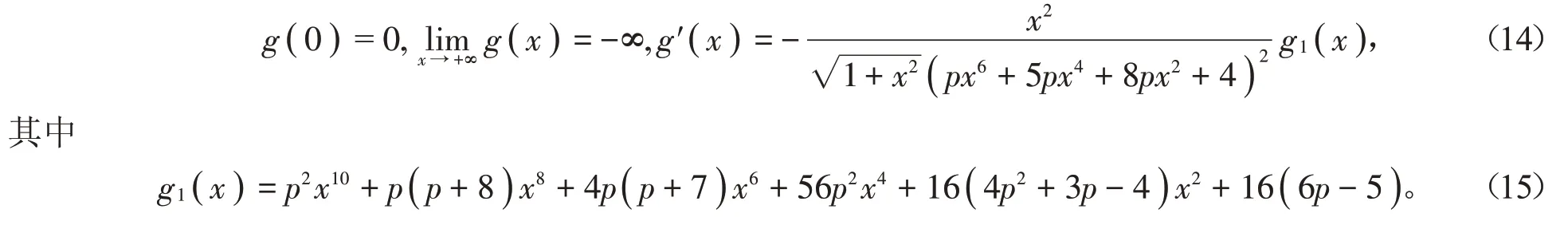
下面分兩種情形討論：

（1）當p=5∕6時，等式（15）化簡為

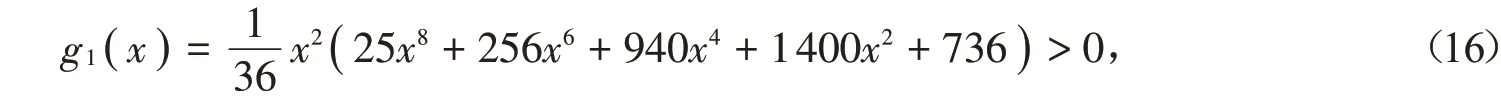
對所有x ∈( 0,+∞ )成立。所以，由（14）、（16）式得到對所有x ∈( 0,+∞ )有g( x )＜0。

（2）當p=1∕2時，由（15）式可推得

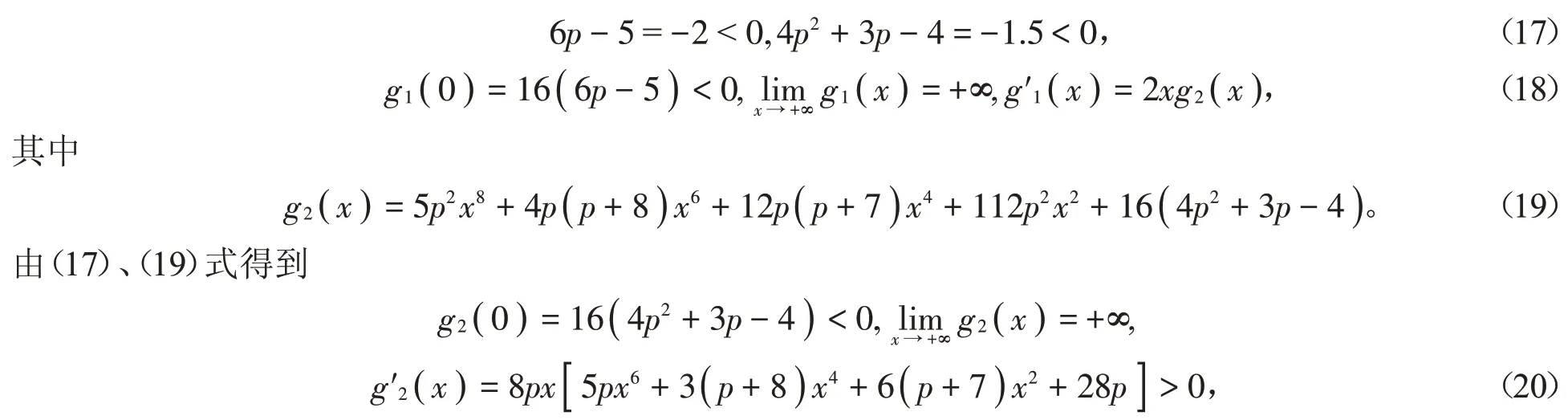
由（20）式可知存在μ0∈( 0,+∞ )使得當x ∈( 0,μ0)時g2( x )＜0，當x ∈( μ0,+∞ )時g2( x )＞0。由（18）式可知，當x ∈( 0,μ0)時g1( x )＜0；當x ∈( μ0,+∞ )時，g1( x )在區間( μ0,+∞ )內嚴格單調上升且g1( μ0)＜0，易知存在μ1＞μ0使得當x ∈( μ0,μ1)時g1( x )＜0，當x ∈( μ1,+∞ )時g1( x )＞0。綜上可知，當x ∈( 0,μ1)時g1( x )＜0；當x ∈( μ1,+∞ )時g1( x )＞0。

同上分析，由（18）和（19）式，結合x ∈( 0,μ1)時g1( x )＜0，x ∈( μ1,+∞ )時g1( x )＞0，易知存在μ ＞μ1使得當x ∈( 0,μ )時g( x )＞0；當x ∈( μ,+∞ )時g( x )＜0。

下面給出本文的主要結論及證明。

定理1 雙向不等式α1A(a,b)+ ( 1-α1)H(a,b)＜NQG(a,b)＜β1A(a,b)+ ( 1-β1)H(a,b)對所有a,b ＞0且a ≠b成立當且僅當α1≤∕2=0.707 1…，β1≥5∕6。

證明 根據調和平均H(a,b)，算術平均A(a,b)和Neuman平均NQG( a,b )是對稱且一階齊次的，不失一般性，假設a ＞b ＞0，設p ∈( 0,1 )和x= ( a-b )∕∈( 0,+∞)，則由（1）～（4）式得到

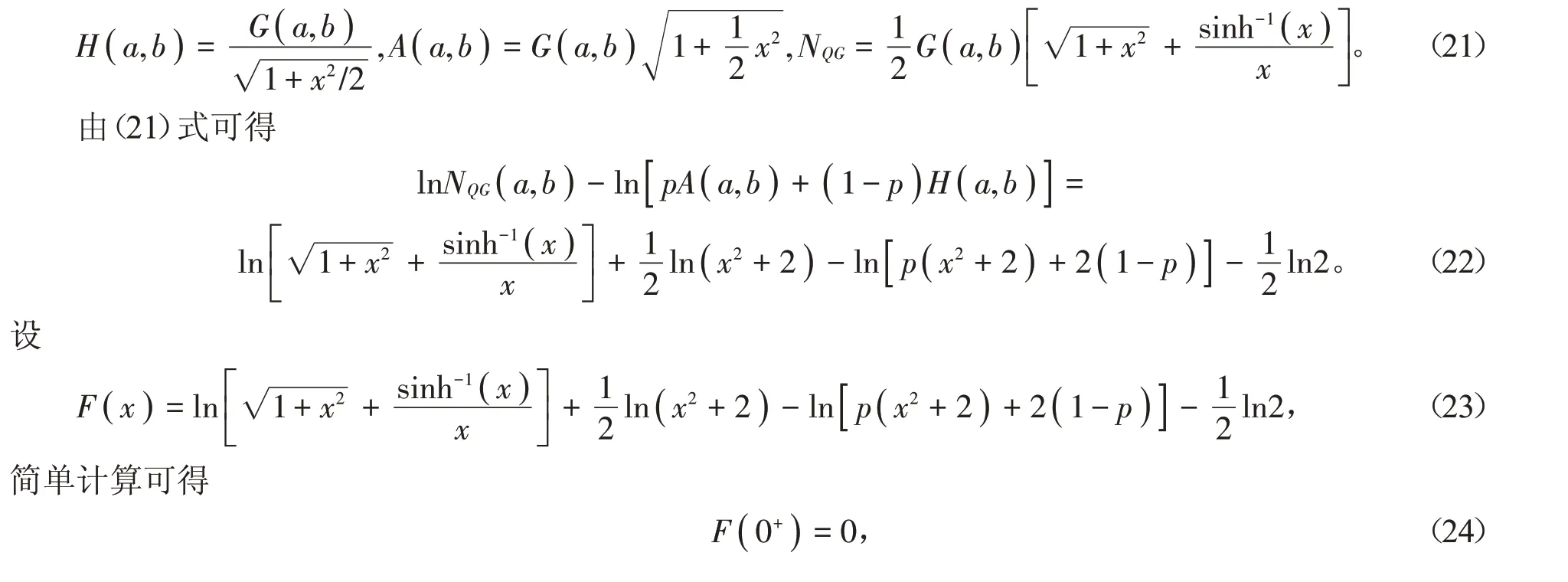
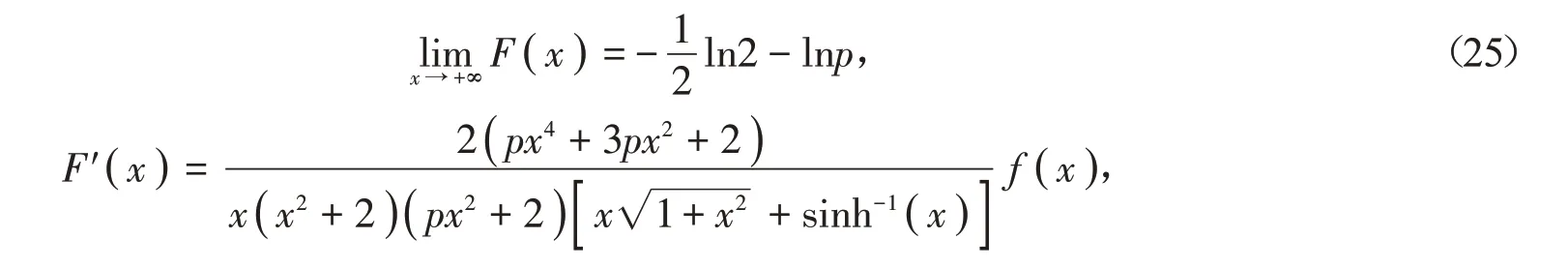
其中f(x)同引理1中定義。

下面分4種情形證明。

（1）如果p=5∕6，由（22）～（24）式和引理1（1）可知NQG( a,b )＜A( a,b )+H( a,b )對所有a,b ＞0且ab成立。

（3）如果p ＜5∕6，x ＞0和x →0，則應用冪級數展開得到

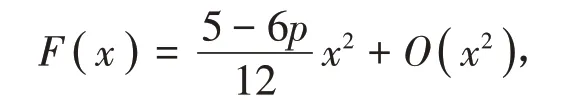
進一步由（22）、（23）式知，存在一個充分小實數δ0=δ0( p )＞0使得對所有( a-b )∕∈( 0,δ0)恒有

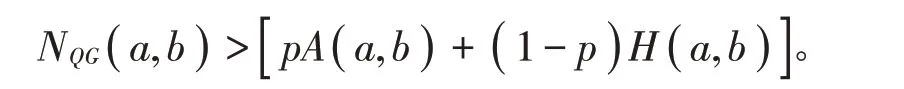
證明 不失一般性，假設a ＞b ＞0。設p ∈( 0,1 )和x= ( a-b )∕∈( 0,+∞)，則由(21)式得到

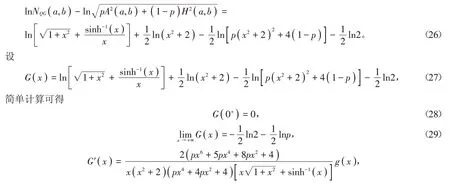
（1）如果p=1∕2，由（28）式和引理2（2）知存在一個μ ∈( 0,+∞ )使得函數G( x )在x ∈( 0,μ )內嚴格單調上升及在x ∈( μ,+∞ )內嚴格單調下降。注意到G( x )=0，所以由（26）～（28）式和協同函數G( x)的分段單調性可知對所有a,b ＞0且a ≠b成立。

（2）如果p=5∕6，由（26）～（28）式和引理2（1）可知a,b ＞0且a ≠b成立。