關(guān)于一類數(shù)字半群的Frobenius問題

吳 琳，孫廣人，凌 燕，潘 萍

（安慶師范大學(xué)數(shù)學(xué)與計(jì)算科學(xué)學(xué)院，安徽安慶246133）

19世紀(jì)末，德國(guó)數(shù)學(xué)家Frobenius根據(jù)硬幣問題提出了著名的Frobenius問題：給定一組正整數(shù)系數(shù)l1,l2,…,lp( p ∈?+)，求出使不定方程Y =l1x1+l2x2+…+lpxp沒有非負(fù)整數(shù)解的最大正整數(shù)Y。這個(gè)最大正整數(shù)Y則稱為相對(duì)于l1,l2,…,lp的Frobenius數(shù)。同時(shí)，F(xiàn)robenius還證明了當(dāng)方程系數(shù)l1,l2,…,lp的最大公約數(shù)等于1時(shí)，F(xiàn)robenius數(shù)就一定存在。之后，隨著Frobenius問題研究的深入，進(jìn)而產(chǎn)生了數(shù)字半群這一新概念。

下面給出數(shù)字半群的基本概念[1]。令?是所有非負(fù)整數(shù)構(gòu)成的集合，若?的子集S在加法下封閉，0 ∈S且?S有限，則稱S是數(shù)字半群。給定?的一個(gè)非空子集A，用A 表示由A生成的( )?,+ 的一個(gè)幺子半群，即

此外，A 為數(shù)字半群當(dāng)且僅當(dāng)集合A中的所有元素的最大公約數(shù)為1。對(duì)于數(shù)字半群S，若S滿足條件S= A ，則稱A是S的生成元系，集合A中的元素稱為S的生成元；若A的任意真子集都不能生成S，則稱A是S的極小生成元系。每個(gè)數(shù)字半群S都有唯一的一個(gè)極小生成元系并且這個(gè)極小生成元系中的元素個(gè)數(shù)也都是有限的，也就是說每個(gè)數(shù)字半群都是有限生成的[2]，數(shù)字半群S的極小生成元系中的元素個(gè)數(shù)稱為S的嵌入維數(shù)，用e( )S 表示；對(duì)于不能用數(shù)字半群的極小生成元系線性表示的最大正整數(shù)，即不屬于S的最大正整數(shù)，稱為數(shù)字半群S的Frobenius數(shù)，用F(S) 表示。由此可知，F(xiàn)robenius問題的數(shù)字半群形式為給定數(shù)字半群的一組生成元，求出只和生成元系有關(guān)的F(S)計(jì)算公式。數(shù)字半群的Frobenius問題是一個(gè)經(jīng)典問題[3-7]。目前，嵌入維數(shù)為2的數(shù)字半群Frobenius問題及許多相關(guān)問題已經(jīng)得到了解決[8]。但是，對(duì)于嵌入維數(shù)不小于3的數(shù)字半群，這些問題都是N-P問題[9]，因此一些特殊數(shù)列生成的數(shù)字半群一直是研究熱點(diǎn)[2,10-11]。

對(duì)于固定的n ∈?，Thabit數(shù)字半群T( n )是由數(shù)列3·2n+i-1( i ∈? )生成的，若將數(shù)列通項(xiàng)公式中的系數(shù)3變成任意的一個(gè)奇數(shù)2m-1(m ∈?且m ≥1)，此時(shí)新的數(shù)列( 2m-1 )·2n+i-1( i ∈? )生成的數(shù)字半群就是數(shù)字半群T( m,n )[12]。文獻(xiàn)[12]中已經(jīng)確定了T( m,n )的極小生成元系并且求出了Frobenius數(shù)的計(jì)算公式，解決了T( m,n )的Frobenius問題，而本文將對(duì)數(shù)字半群T( m,n )更加一般的數(shù)字半群繼續(xù)研究同樣的問題。對(duì)于固定的n ∈?，m ∈? 且m ≥1，將數(shù)列( 2m-1 )·2n+i-1( i ∈? )系數(shù)中的1 變成任意的奇數(shù)k并且規(guī)定1≤k ＜2m-1，這時(shí)生成的數(shù)字半群為T( m,k,n )=通過一系列的歸納論證探究了新數(shù)字半群T( m,k,n )的極小生成元系，嵌入維數(shù)和Apéry集等方面的性質(zhì)，又針對(duì)k=2m-1 和k=2t-1（t ∈? 且t ≥1）這兩種特殊情況，研究了T( m,k,n )的Frobenius 數(shù)，求出了這兩種情況下的數(shù)字半群T( m,k,n )的Frobenius數(shù)計(jì)算公式。

1 嵌入維數(shù)e( T( m,k,n))

令m，n為兩個(gè)正整數(shù)且2 ≤m ≤2n，令k是奇數(shù)且1≤k ＜2m-1，則

引理1[12]令S是由非空集合A生成的數(shù)字半群，則下列條件等價(jià)：

（1）?a ∈A,2a+1∈S；（2）?s ∈S{ 0 }，2s+1∈S。

在引理1的基礎(chǔ)上可以得到下面的結(jié)論。

引理2 若m，k，n ∈?，2 ≤m ≤2n，k為奇數(shù)且1≤k ＜2m-1，則T( m,k,n )=

證 明 令S′= { s0,s1,…,sn+m-1}，顯 然S′?T( m,k,n )。接 下 來 要 證 明T( m,k,n )?S′，若i ∈{ 0,1,…,n+m-2 }，則2si+1=si+1∈S′。對(duì)于i=n+m-1，有

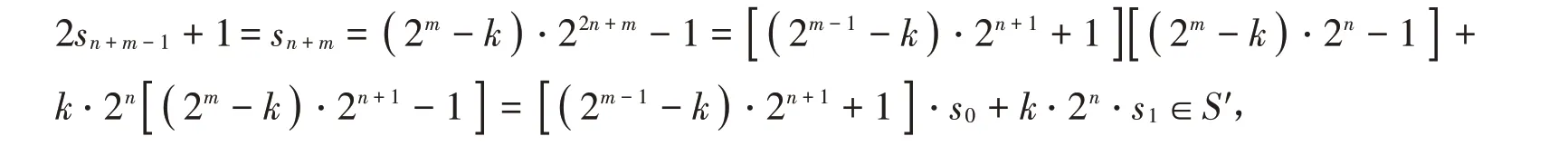
根據(jù)引理1，可得對(duì)于?s′∈S′{ 0}（這里用s′表示數(shù)字半群S′中的任意一個(gè)元素），有2s′+1∈S′。

綜上可得，對(duì)于i ≥m，有sn+i∈S′，即T( m,k,n )?S′。同時(shí)可知{ s0,s1,…,sn+m-1}是數(shù)字半群T( m,n,k )的生成元系，下面在此基礎(chǔ)上證明{ s0,s1,…,sn+m-1}是T( m,k,n )的極小生成元系。

引理3 若m，k，n ∈?，2 ≤m ≤2n，k為奇數(shù)且1≤k ＜2m-1，則sn+m-1?

證明 證明方法過程與文獻(xiàn)[12]中引理2.3相同。

根據(jù)引理3確定了T( m,k,n )的極小生成元系，再由嵌入維數(shù)的概念便得到了定理1。

定 理1 若m ，k ，n ∈? ，2 ≤m ≤2n，k 為 奇 數(shù) 且1≤k ＜2m-1，則e( T( m,k,n ))=n+m 且{s0,s1,…,sn+m-1}是T( m,k,n )的極小生成元系。

證明 根據(jù)引理2和引理3即證。

2 T( m,k,n )的Apéry集

下面主要探究數(shù)字半群T( m,k,n )的Apéry集方面的一些性質(zhì)。

令S 是數(shù)字半群，x ∈S{ 0 }，定義S 中x 的Apéry 集[1]為Ap( S,x )={ s ∈S |s-x ?S }，而Ap( S,x )集合的勢(shì)等于x，記Ap( S,x )={ ω( 0 ),ω( 1 ),…,ω( x-1 )}。這里，對(duì)?i ∈{ 0,1,…,x-1 }，ω( i )是S中與i模x同余的最小元素。

注1 用A( r )表示所有元素( a1,a2,…,ar)∈{ 0,1,2}r的集合且元素( a1,a2,…,ar)滿足條件：若1≤i ＜j ＜r,aj=2, 則ai=0。

引理5 若m，k，n ∈?，2 ≤m ≤2n，k為奇數(shù)且1≤k ＜2m-1，令T( m,k,n )是由{ s0,s1,…,sn+(m-1)}極小生成的數(shù)字半群，則

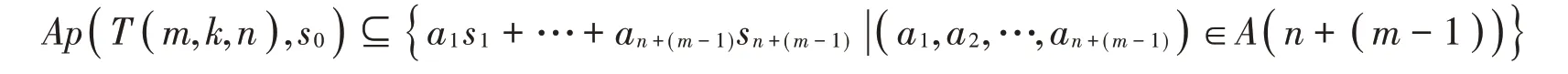
證明 證明過程[12]中引理3.1相同。

引理6[10]在常設(shè)符號(hào)下，若m，k，n ∈?，2 ≤m ≤2n，k 為奇數(shù)且1≤k ＜2m-1，若x′∈T( m,k,n )，x′≡0 mod s0不成立，則x′-1∈T( m,k,n )。

引理7[10]在常設(shè)符號(hào)下，若m，k，n ∈?，2 ≤m ≤2n，k 為奇數(shù)且1≤k ＜2m-1，令ω( i )是T( m,k,n )中與i模s0同余的最小元素，則?i ∈{ 0,1,…,s0-1 }，ω( 0 )＜ω( 1 )＜…＜ω( s0-1 )。

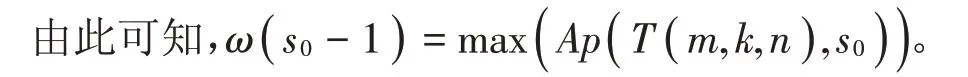
上述引理5并沒有得到T( m,k,n )的一個(gè)確切Apéry集，而且當(dāng)k不同時(shí)，數(shù)字半群T( m,n,k )對(duì)應(yīng)的Apéry集都不相同，情況比較復(fù)雜。因此下面將針對(duì)k=2m-1-1和k=2t-1（t ∈?且t ≥1）這兩種特殊情況，探究使引理5等號(hào)成立的條件，確定這兩種情況下的T( m,k,n )的Apéry集，進(jìn)而求出Frobenius數(shù)計(jì)算公式。

3 k=2m-1 -1時(shí)，T( m,k,n )的Frobenius數(shù)

這里，令k=2m-1-1，則2m-k=2m-1+1，所以

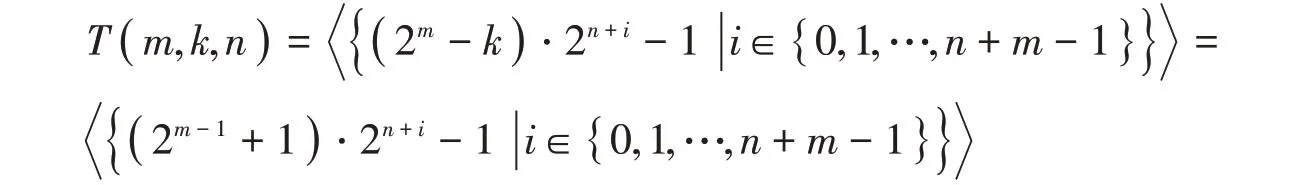
且e( T( m,k,n ))=n+m，而對(duì)于?i ∈?，這里si= ( 2m-1+1 )·2n+i-1∈T( m,k,n )。

注2 （1）設(shè)X是一個(gè)非空集合，P為條件，因此定義#X表示集合X的勢(shì)；X |P是指滿足條件P的X的子集。

（2）令r是正整數(shù)，( a1,a2,…,ar)，( b1,b2,…,br)∈A( r )，在A( r )上定義如下關(guān)系：

( a1,a2,…,ar)≤r( b1,b2,…,br)??m′＞0,am′=bm′或?m′＞0,?i ＜m′,am′＜bm′,ai=bi，

由此可知≤r是A( r )上的全序。

引理8 在常設(shè)符號(hào)下，若m，k，n ∈?，2 ≤m ≤2n，k=2m-1-1，則max( Ap( T( m,k,n ),s0))≤sn+sn+(m-1)。

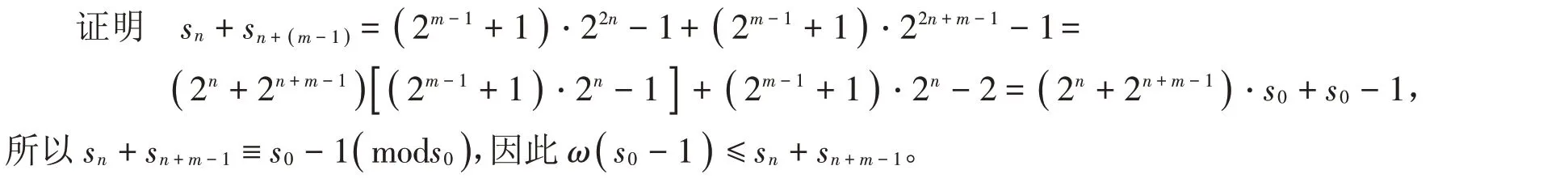
根據(jù)引理8，可以得到如下結(jié)論。

引理9 在常設(shè)符號(hào)下，若m，k，n ∈?，2 ≤m ≤2n，k=2m-1-1，則

（1）2sn+m-1?Ap( T( m,k,n ),s0)；

（2）對(duì)?i ∈{ 0,1,…,n+m-1 }，sn+sn+m-1+si?Ap( T( m,k,n ),s0)。

注3 現(xiàn)定義R( n+m-1 )是滿足下列條件序列( a1,a2,…,an+m-1)∈A( n+m-1 )的集合：

①an+m-1∈{ 0,1 }；

②若n ＜i ＜n+m-1，an=an+m-1=1，則ai=0，同時(shí)，令( a′1,a′2,…,a′n-1)∈A( n-1 )，則R( n+m-1 )= A( n+m-1 )|( a1,a2,…,an+m-1)≤n+m-1( a′1,a′2,…,a′n-1,1,0,…,0,1 )。

引理10 在常設(shè)符號(hào)下，若m，k，n ∈?，2 ≤m ≤2n，k=2m-1-1，則

證明 下面分成2種情況進(jìn)行討論。

（1）若( a1,…,an+m-1)∈R( n+m-1 )，2 ?{ a1,…,an+m-1}，則對(duì)于?i ∈{ 1,2,…,n-1 }，ai∈{ 0,1 }。

又因?yàn)? an,an+1,…,an+m-2,an+m-1)≤m( 1,0,…,0,1 )，所以

①當(dāng)( an,an+1,…,an+m-2,an+m-1)＜m( 1,0,…,0,1 )時(shí)，#R( n+m-1 )=2n-1·( 2m-1+1 )；

②當(dāng)( an,an+1,…,an+m-2,an+m-1)= ( 1,0,…,0,1 )時(shí)，#R( n+m-1 )=1。

因此，# R( n+m-1 )|2 ?{ a1,…,an+m-1}= ( 2m-1+1 )·2n-1+1=2n+m-2+2n-1+1。

（2）若( a1,…,an+m-1)∈R( n+m-1 )，2 ∈{ a1,…,an+m-1}，則

①當(dāng)2 ∈{ an,…,an+m-1}時(shí)，# R( n+m-1 )|2 ∈{ an,…,an+m-1}=2m-1-1；

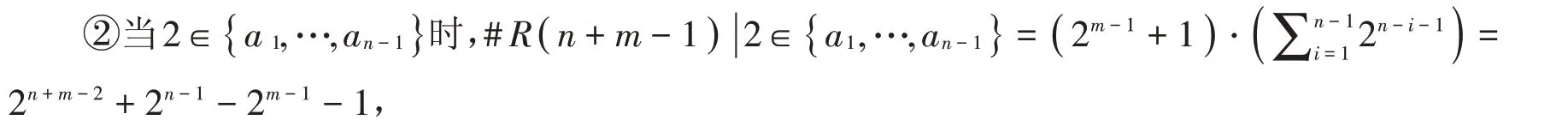
所以# R( n+m-1 )|2 ∈{ a1,……,an+m-1}=2n+m-2+2n-1-2m-1-1+2m-1-1=2n+m-2+2n-1-2

因此，綜合上述有#R( n+m-1 )=2n+m-1+2n-2+1 = ( 2m-1+1 )·2n-1。

根據(jù)上述引理的證明，得到了如下當(dāng)k=2m-1-1時(shí)，引理5等號(hào)成立時(shí)的情況。

定理2 在常設(shè)符號(hào)下，若m，k，n ∈?，2 ≤m ≤2n，k=2m-1-1，令T( m,k,n )是由{ s0,s1,…,sn+(m-1)}極小生成的數(shù)字半群，則

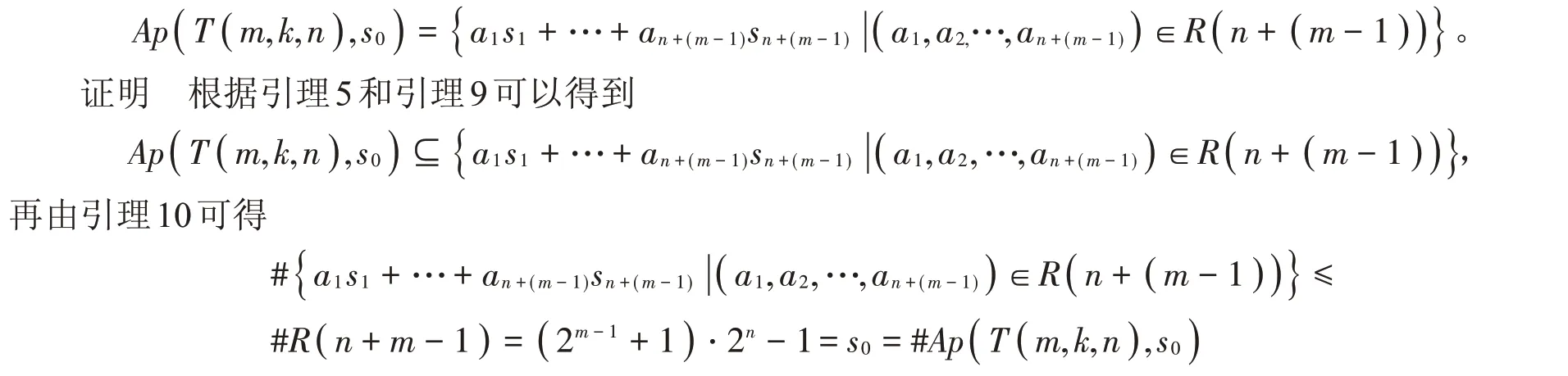
令S 是數(shù)字半群，x ∈S{ 0 }，已知F( S )=max Ap( S,x )-x[1]，因此可以得到如下關(guān)于T( m,k,n )的Frobenius數(shù)計(jì)算公式。

推論1 在常設(shè)符號(hào)下，若m，k，n ∈?，2 ≤m ≤2n，k=2m-1-1，則

4 k=2t -1( t ≥1 )時(shí)，T( m,k,n )的Frobenius數(shù)

這里，k=2t-1（這里t ∈?且t ≥1），則2m-k ＞0，故m ≥t+1，所以

引理11[12]令r是正整數(shù)，則#A( r )=2r+1-1。

引理13 在常設(shè)符號(hào)下，若m，k，n ∈?，k=2t-1(t ∈?且t ≥1)，t+1≤m ≤2n，則

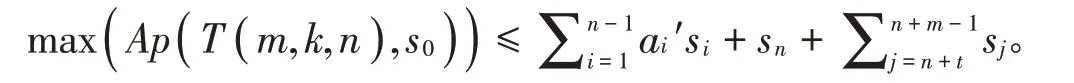
證明 對(duì)?i ∈?，有si=+2i-1，

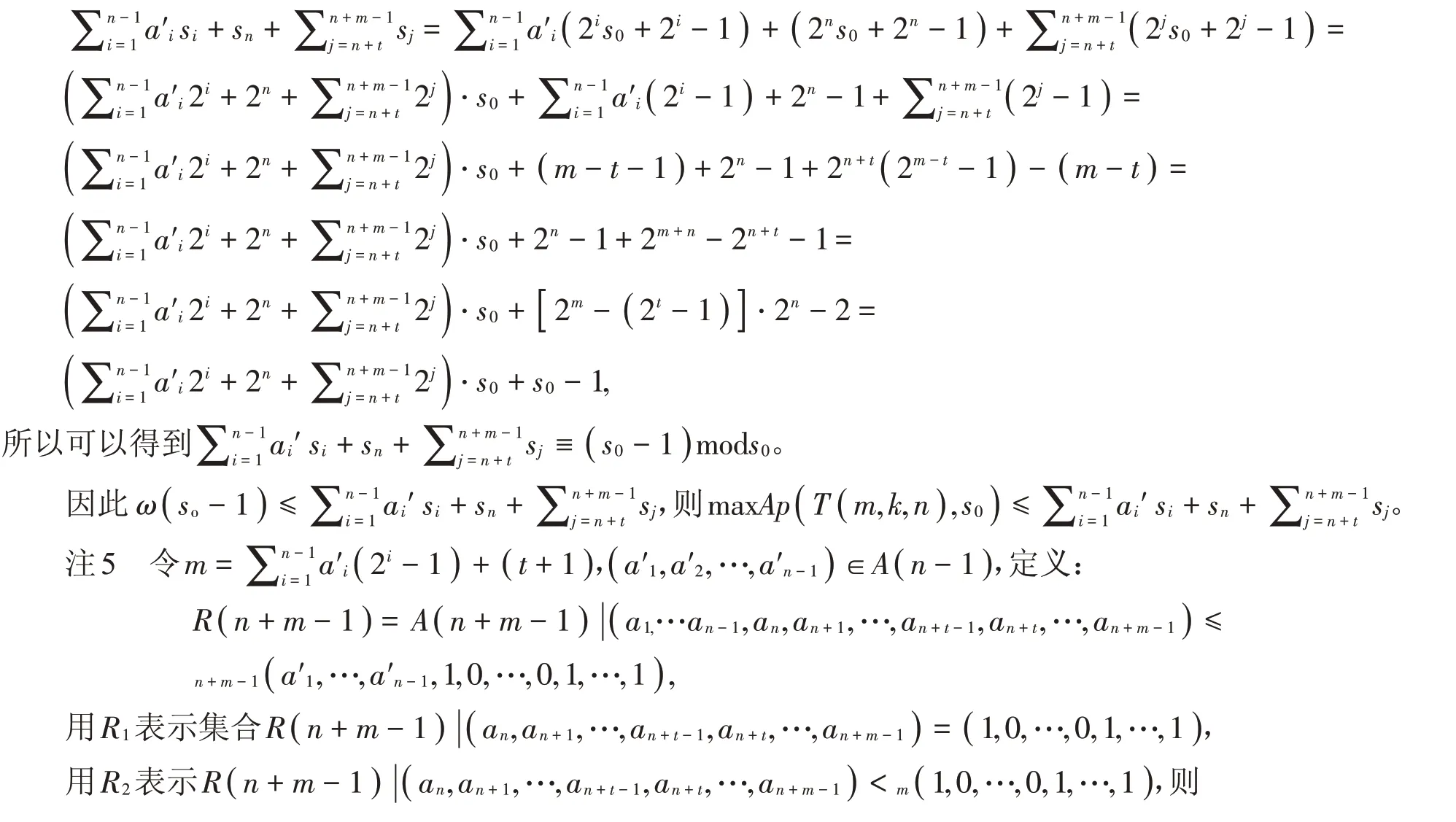
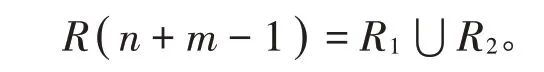
引理14 在常設(shè)符號(hào)下，若m,k,n ∈?，k=2t-1（t ∈?且t ≥1），t+1≤m ≤2n，則

此時(shí)分2種情況進(jìn)行討論：

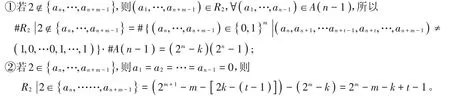
因此，綜合上述有

根據(jù)上述引理證明，可以得到關(guān)于k=2t-1（t ∈?且t ≥1）時(shí)T(m,k,n) 的確切的Apéry集。

定理3 在常設(shè)符號(hào)下，若m，k，n ∈?，k=2t-1(t ∈? 且t ≥1)，t+1≤m ≤2n，令T(m,k,n) 是由{s0,s1,…,sn+(m-1)}極小生成的數(shù)字半群，則

推論2 常設(shè)符號(hào)下，若m，k，n ∈?，k=2t-1(t ∈?且t ≥1)，t+1≤m ≤2n，則

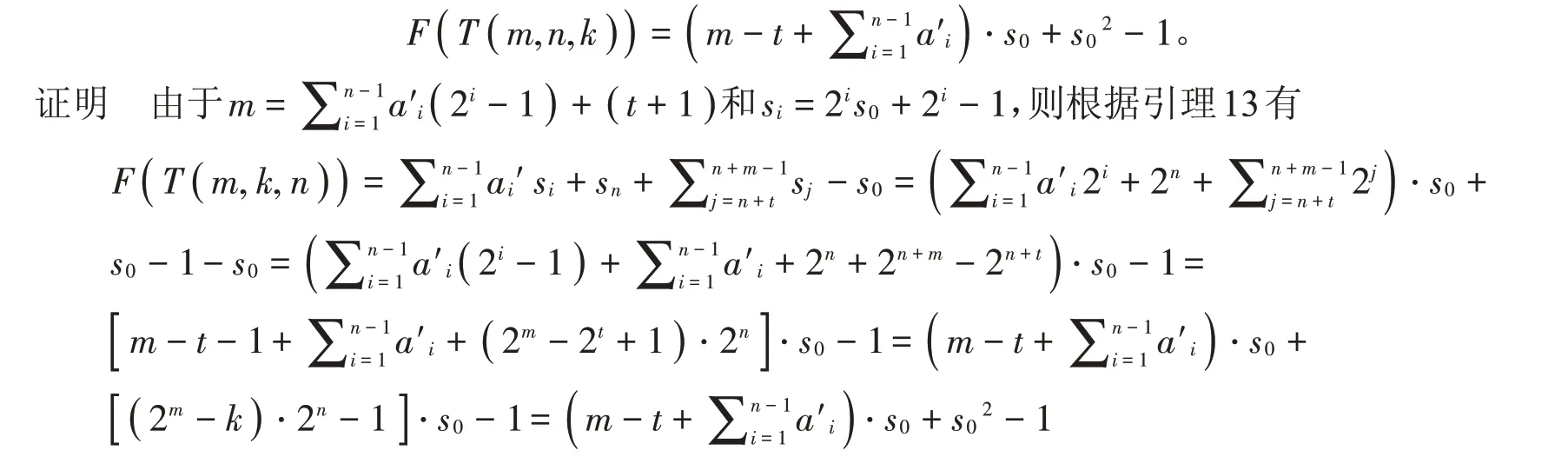
例2 令t=2，則k=3，所以令m=4時(shí)，T( 4,3,n )=13·2n+i-1 |i ∈?，再令n=2，則根據(jù)定理1 可知51,103,207,415,831,1663是T( 4,3,2 )的極小生成元系，e( T( 4,3,2 ))=6。根據(jù)引理14 可得

所以根據(jù)定理3可知

5 結(jié)束語

本文在Gu等人研究的數(shù)字半群基礎(chǔ)上，研究了新數(shù)字半群T( m,k,n )的Frobenius問題，但由于不同k的取值導(dǎo)致數(shù)字半群T( m,k,n )的Frobenius數(shù)的計(jì)算公式也不同，情況多而復(fù)雜，所以這里只探討其中兩類情況。而對(duì)于k的其他取值情況下，數(shù)字半群T( m,k,n )的Frobenius問題仍然有待于我們繼續(xù)深入探究。